Mechanism and kinetic study on the ring-opening degradation of 2,3,7,8-tetrachlorinated dibenzofuran initiated by OH radicals in waste incineration†
Abstract
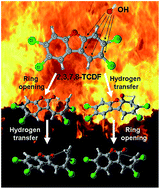
The ring-opening degradation mechanism of 2,3,7,8-tetrachlorinated dibenzofuran (2,3,7,8-TCDF) initiated by OH radicals is investigated using density functional theory. On the basis of the bimolecular reactions of 2,3,7,8-TCDF with OH radicals, the main study is focused on the subsequent unimolecular reactions, including ring-opening, hydrogen transfer and other chemical transformations. There are thirty-five reaction channels established according to the different reaction process. Ab initio calculations and reaction dynamic calculations are performed for all the reaction channels, and the calculated results are consistent with the available reported data, providing a detailed knowledge of the ring-opening degradation of 2,3,7,8-TCDF initiated by OH radicals. Generally, OH radicals can promote the ring-opening degradation of 2,3,7,8-TCDF, and the decomposition threshold temperature range of 2,3,7,8-TCDF is 500–850 K, which can serve as the technology parameter of the elimination of dioxins.

 Please wait while we load your content...
Please wait while we load your content...