Kinetics of the oxidation of isoniazid with the hypochlorite ion†
Virág Bogdándi,
Gábor Lente* and
István Fábián
Department of Inorganic and Analytical Chemistry, University of Debrecen, Debrecen, Hungary. E-mail: lenteg@science.unideb.hu
First published on 30th July 2015
Abstract
The stoichiometry and kinetics of the reaction between isoniazid (isonicotinic hydrazide, INH) and the hypochlorite ion was studied in a basic aqueous medium (pH > 10) by spectrophotometric, hydrogen-1 nuclear magnetic resonance, electrospray mass spectrometric and stopped-flow methods. At oxidant excess, the sole organic product was confirmed to be isonicotinic acid. At isoniazid excess, a coupled condensation product formed from isoniazid and isonicotinic acid was also detected in relatively high amounts. The stoichiometric ratio of the two reactants (INH/OCl−) was 0.46 or 0.67 depending on which of the reagents was in excess initially. Under all conditions, the rate determining step of the overall reaction was confirmed to be the rapid bimolecular reaction between the neutral from of isoniazid and the anionic hypochlorite ion. The second order rate constant of the process was estimated to be (3.4 ± 0.7) × 104 M−1 s−1 at 25.0 °C.
Introduction
According to the World Health Organization, tuberculosis, caused by the microorganism Mycobacterium tuberculosis, is one of the world's deadliest communicable diseases.1 About 9 million people developed the disease in 2013 and 1.5 million died as a consequence of this infection, which is in sharp contrast with the fact that tuberculosis is almost fully preventable by today's pharmaceuticals. Isoniazid (isonicotinic hydrazide, INH in Scheme 1) is the most important first-line antibiotic used to fight this disease. It is estimated that 37 million lives were saved between 2000 and 2013 through the effective diagnosis and treatment of tuberculosis.1Isoniazid was introduced into clinical practice in the 1950s. Since then, a lot of efforts have been devoted to study the molecular background of its specific antimycobacterial activity and the possible emergence of resistance to it. It seems now clear that the oxidation of isoniazid plays a major role both in its mechanism of action and metabolism in the body.2–16 The activation of isoniazid is carried out by a catalase-peroxidase enzyme: it involves coupling it to a NADH,4,6–8 and the resulting complex is a strong inhibitor of the enoyl-acyl carrier protein reductase enzyme,9 and consequently stops the synthesis of mycolic acid, which is required for building the bacterial cell wall. Because of this mechanism, there is still active research aimed at understanding the oxidation patterns of isoniazid under a variety of conditions.14–16
Hypochlorous acid and its conjugate base, hypochlorite ion, are ubiquitous in biological systems. This simple inorganic oxidant is produced by neutrophils to fight invading microbes and also has a role in inflammations.17–22 It is the product of the myeloperoxidase-catalyzed oxidation of chloride ion in the presence hydrogen peroxide17,22 and may react with a whole range of organic and inorganic reactants in the body. The kinetics of these processes has an obviously important role in governing the typical concentrations of available HOCl/OCl−.20,21,23,24 An additional, and industrially very important interest in the reactions of hypochlorite ion stems from the use of chlorination in water treatment technologies.23–28
In this paper, we report a detailed experimental study of the reaction between isoniazid and hypochlorite ion. In addition to the mentioned biological relevance, there are various points of chemical interest in this process as well. A flow injection determination of isoniazid was reported earlier based on chemiluminescence after reaction with electrogenerated hypochlorite ion.29–31 The oxidation methods of acid hydrazides are also of interest in organic chemistry typically as a tool in peptide synthesis or as a de-protection strategy to obtain carboxylic acids.32–38
At this point, it should be mentioned that there is an earlier kinetic study published on the reaction between isoniazid and hypochlorite ion in basic medium.39 In that work, the process was followed through sampling and offline analysis by iodometric titration. Reportedly, typical reaction lifetimes were several minutes or even hours. Our own observations contrast this earlier report39 very sharply. Three independent methods (spectrophotometry, NMR and mass spectrometry) showed that the reaction between isoniazid and hypochlorite ion is complete within 5 s. Furthermore, the earlier study reported a retarding effect of added chloride ion,39 which is unreasonable for hypochlorite ion reactions in the basic range as chloride ion does not participate in any reaction under these conditions.23,24 The earlier work39 assumed that hypochlorite ion can be selectively monitored in this system by iodometric titration. In fact, literature results show that isoniazid reacts with iodine readily.40 Therefore, it is impossible to determine the concentration of hypochlorite ion by this method in the presence of excess isoniazid. Consequently, the conclusions reported in that earlier study39 must be entirely flawed. One might speculate that a completely erroneous signal was followed by iodometry in the earlier work,39 which might have arisen because of the known influence of ambient oxygen during iodometric titrations at longer times. However, because sufficiently detailed description of the experimental procedures is not reported in the article,39 it is very difficult to assess what the exact origin of the misleading conclusion was.
The objective of this work was to study the reaction of isoniazid with hypochlorite ion through establishing the stoichiometry and the rate equation of the process. Another aim was to interpret this rate equation on a molecular basis. The reaction itself was expected to be a potential source of active isoniazid loss during tuberculosis treatment, when the body produces significant amount of hypochlorite ion to fight the infection, therefore contributing to the interpretation of the well-known need for unusually high therapeutic doses.1–5 In addition, characterizing the process was expected to yield more insights into the metabolism of isoniazid.
Experimental section
Materials
All solutions were prepared using ion exchanged and ultrafiltered water from a MILLI-Q RG system. All chemicals were commercially available and of reagent grade. Isoniazid stock solutions were prepared from solid isoniazid (Fluka Analytical, Sigma-Aldrich). The purity of this material was checked by 1H-NMR measurements: no signals have been detected in addition to the resonances attributed to isoniazid. Isonicotinic amide and isonicotinic acid (both from Sigma-Aldrich) were used as received from the vendor. They were also shown to be pure by 1H-NMR.Chloride ion free solutions of sodium hypochlorite were prepared as described earlier in the literature.23–25,41 The concentrations of NaOCl solutions were determined by iodometric titration,23–25,41 whereas the concentration of excess NaOH in the same solution was determined by acid-base titration with perchloric acid as detailed in a previous paper.24 In all kinetic measurements, constant ionic strength was maintained by adding an appropriate amount of NaClO4. High purity sodium perchlorate was specially prepared for this purpose by a literature method.42 Solutions of sodium hydroxide were prepared from solid NaOH and their concentrations were standardized by routine acid–base titration against primary standard potassium hydrogen phthalate (Reanal). NaCl (Sigma-Aldrich) was used as an additive in some experiments. For NMR experiments, D2O and NaOD (40% in D2O) were purchased from Sigma-Aldrich and used without further purification.
Instrumental measurements
UV-vis spectra were recorded and spectrophotometric titrations were carried out on PerkinElmer Lambda 25, PerkinElmer Lambda 2S or Shimadzu UV-1800 scanning spectrophotometers and sometimes on an Agilent 8543 diode-array spectrophotometer. In this latter case, special care was taken to avoid any photochemical interference caused by the intense analyzing light beam of the instrument.43–45 The letter A is used to refer to the measured absorbance value throughout this paper. Standard quartz cuvettes of 1.000 cm path length (Hellma) were used along with divided (tandem) quartz cells of 2 × 0.454 cm (Hellma). As the studied reactions were fast, detailed kinetic measurements were performed with an Applied Photophysics DX-17 MV sequential stopped-flow apparatus using 1.00 cm optical path length. The dead time of the instrument was measured to be 1.09 ± 0.02 ms by published methods.46,47 In some experiments, an Applied Photophysics PD.1 Photodiode Array accessory was used as a detector of the stopped-flow instrument. Some semi-quantitative kinetic measurements were also performed in the Agilent 8543 diode-array spectrophotometer using an RX-2000 Applied Photophysics Rapid Kinetics Accessory. Kinetic experiments were repeated at least five times to prove the reproducibility of the measured traces. Most titrations were carried out by a Metrohm 785 DMP Titrino automatic titrator equipped with Metrohm 6.0451.100 combination platinum and Metrohm 6.0262.100 combination glass electrodes. Routine 1H-NMR spectra were recorded on a Bruker Avance 360 NMR spectrometer. Typically, the spectra were referenced on the residual signal of D2O.ESI-MS measurements were carried out with a Bruker micrOTOFQ mass spectrometer equipped with a quadrupole and time-of-flight (Q-TOF) analyzer in positive ion mode. The nebulizer pressure was set to 6 psi, N2 was used as drying gas at 4 l min−1, the temperature was maintained at 160 °C, and the applied capillary voltage was −3.0 kV. The typical error of mass measurement was below 0.005 in the m/z range from 80 to 600. Spectra were accumulated and recorded by a digitizer at a rate of 2 GHz.
Softwares
The raw data sets of the measurements were processed with the dedicated instrument controlling softwares (Perkin-Elmer, Shimadzu, Agilent, Applied Photophysics, Bruker). Additional transformation of the data was sometimes made using Microsoft Excel 2003. Typically, Micromath Scientist 2.0, Microcal Origin 6.1 and Matlab were used for Levenberg–Marquard least-squares fitting procedures. Some additional processing of NMR measurements was done using the software MestReNova 10.0.0.Results and discussion
Preliminary observations
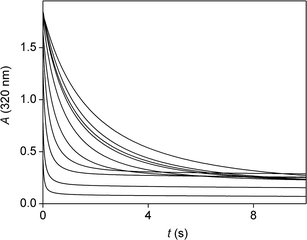
Experiments were carried out primarily in basic medium where hypochlorite ion is not protonated or transformed into chlorine. Mixing a solution of isoniazid with a solution of sodium hypochlorite at relatively high concentrations was accompanied by visible bubble formation. This is understood to be indicative of the formation of nitrogen gas (N2), which is one of the products of the reaction. In all later experiments, some care had to be taken to avoid the negative interference of bubble formation with the spectrophotometric detection method. During spectrophotometric titrations, samples were shaken well after the addition of each increment of the titrant and it was made sure that no bubbles remain in the path of the light beam. The problem was worse for kinetic measurements: the only way to avoid interference in this case was to limit the concentration range of the studies to relatively dilute solutions in which no bubble formation occurred.Stopped-flow experiments showed that the redox reaction between the two reagents was quite fast: spectral changes were over within 5 s in all cases. Fig. 1 shows typical spectral changes in the UV range during the course of the process. Under these particular conditions, the absorbance change is complete within 2 s. The ratio of the initial reactants in this experiment is close to stoichiometric as it is confirmed later. Both hypochlorite ion and isoniazid have absorptions in this spectral region, so the initial spectrum reflects the combination of these absorbance contributions. The final spectrum is dominated by the organic final product as chloride ion does not have light absorption in this spectral region. Further preliminary spectrophotometric experiments showed that it is possible to monitor the concentration change of isoniazid with high selectivity at 320 nm. Therefore, this wavelength was selected for later kinetic studies.
Stoichiometry and product analysis
The extensive spectral changes seen in Fig. 1 made it possible to test the stoichiometry of the reaction by spectrophotometric titration, which is a well-established method for this purpose.48,49 In our experiments, 2.00 cm3 solution of one of the reagents was measured into a standard quartz cell of 1.000 cm path length. This initial solution was titrated with a solution of the other reagent, which was added in 100 μl aliquots. Because of the limited volume of the cell, 15 such portions could be added during one titration. The spectrum of the mixture was recorded after each addition. To make sure that no slow reactions interfered with the process, the mixture was allowed to stand for 2 min and the spectrum was recorded again. In all of our titrations, the spectra measured immediately and 2 min after mixing were identical within experimental error.The results were evaluated using a spectrophotometric titration plot, in which the absorbance was corrected for dilution and plotted as a function of the molar ratios of the two reactants.48,49 The dilution is defined as η = (V + Vini)/Vini, where Vini is the initial volume of the titration (2.00 cm3 in our case), whereas V is the total volume of the added titrant (up to 1.50 cm3 in our experimental setup). When ηA is plotted as a function of the molar ratio of the reactants (as in Fig. 2), a combination of two straight lines is expected for an irreversible process, and the intersection of the two straight lines gives the stoichiometric ratio. This general statement is proved by a detailed derivation that can be found in the ESI. Fig. 2 presents the results of such an analysis of our titration data. Two sets of points are shown as the titration was carried out in both ways. At first, isoniazid was titrated with sodium hypochlorite and the break point occurred at [OCl−]/[INH] = 1.49 ± 0.03. When a solution of NaOCl was titrated with an INH solution in the second case, the break point was observed at [INH]/[OCl−] = 0.46 ± 0.01. It should be added that these plots depend on the wavelength used, but the position of the break point does not. For Fig. 2, the wavelength selection was made to ensure that the break point is determined with the highest accuracy possible. Fig. S1 and S2 in the ESI† show the entire data set recorded during the two titrations, whereas Fig. S3† shows a plot analogous to Fig. 2 but using different wavelengths. Fig. S4† also proves that the absorbance measured in the kinetic experiment shown in Fig. 1 at 260 nm correlates linearly with the absorbance measured at 320 nm. Therefore, it is clear that these two wavelengths carry the same kinetic information. This is also true for any other wavelengths where meaningful absorbance change can be measured.
In a simple process, it would be expected that the break point of the first titration occurs at the reciprocal of the break point of the second titration (about 2.2). This is clearly not the case here. Yet the plots themselves are combinations of straight lines as expected for a simple reaction. The significant difference between the two titrations is that in the first case (where the break point occurs at 1.49), isoniazid is titrated with hypochlorite ion gradually. Therefore, the process goes under isoniazid excess after the addition of each aliquot. In the other case, hypochlorite is the excess reagent when the reaction proceeds. A simple interpretation of our observations is that the product (or product mixture) is different in these two cases.
Earlier literature results about the oxidation of hydrazide derivatives show that three different oxidized products and three different stoichiometries might be plausible in this case.32–38 These are as follows:
| IN–CONHNH2 + 2OCl− + OH− → IN–COO− + N2 + 2H2O + 2Cl− | (1) |
| 2IN–CONHNH2 + OCl− → 2IN–CONH2 + N2 + H2O + Cl− | (2) |
| 2IN–CONHNH2 + 2OCl− → IN–CONH–NHCO–IN + N2 + 2H2O + 2Cl− | (3) |
Eqn (1) is the four-electron oxidation of isoniazid producing isonicotinic acid (INA, the anion is shown because of the basic medium). In eqn (2), a formally one-electron oxidation produces isonicotinic amide (INM). Eqn (3) shows a coupled product, 2-(4-pyridinylcarbonyl)hydrazide (IND), as a result of a formally two-electron oxidation. It seems that under conditions where OCl− is in excess during the process, eqn (1) with a molar ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 INH
2 INH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OCl− dominates and isonicotinic acid may be the only organic product. Under reverse conditions, however, the lower (ca. 1
OCl− dominates and isonicotinic acid may be the only organic product. Under reverse conditions, however, the lower (ca. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5) INH
1.5) INH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OCl− implies that at least one of the products of eqn (2) and (3) must be formed in significant quantities. As the independent experiments (described in the next paragraphs) never confirmed any formation of isonicotinic amide, it is concluded that the coupled product shown in eqn (3) is responsible for this difference. At oxidant excess, there is some slight deviation from the 0.50 molar ratio expected based on eqn (1), which is 8% and, given the estimated standard errors, probably significant. This slight deviation might be due to the fact that some of the nitrogen atoms of isoniazid are oxidized to nitrate ion:
OCl− implies that at least one of the products of eqn (2) and (3) must be formed in significant quantities. As the independent experiments (described in the next paragraphs) never confirmed any formation of isonicotinic amide, it is concluded that the coupled product shown in eqn (3) is responsible for this difference. At oxidant excess, there is some slight deviation from the 0.50 molar ratio expected based on eqn (1), which is 8% and, given the estimated standard errors, probably significant. This slight deviation might be due to the fact that some of the nitrogen atoms of isoniazid are oxidized to nitrate ion:
| IN–CONHNH2 + 7OCl− + 3OH− → IN–COO− + 2NO3− + 3H2O + 7Cl− | (4) |
An INH/OCl− ratio of 0.46 would imply about 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 N2
2 N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NO3− final molar ratio in the nitrogen-containing products at oxidant excess, which means that nitrate ion would be a very minor by-product.
NO3− final molar ratio in the nitrogen-containing products at oxidant excess, which means that nitrate ion would be a very minor by-product.
As isonicotinic acid (INA) and isonicotinic amide (INM) are available independently, some experiments were carried out with these substrates directly. UV-spectrophotometric experiments revealed no change at all for an hour when isonicotinic acid (INA) was mixed with sodium hypochlorite in aqueous solution (Fig. S5†). On the other hand, isonicotinic amide (INM) underwent significant change in a few minutes when mixed with hypochlorite ion in aqueous solution (Fig. S6†). Therefore, INM is not a plausible product of isoniazid oxidation under these conditions.
Further efforts to identify the products were done by ESI-MS spectrometry. Isoniazid and sodium hypochlorite were mixed in a dilute solution under conditions when INH was in excess. The ESI-MS spectrum of the resulting mixture is shown in Fig. 3. The spectrum confirms the presence of excess isoniazid (the peak at 138.065 corresponds to INH + H+, whereas the peak at 160.047 matches INH + Na+). Two peaks attributable to isonicotinic acid are also visible (146.021: INA + Na+; 168.002: INA − H+ + 2Na+) confirming the identity of this product. As the experiment was done at an excess of isoniazid, formation of the coupled product IND is possible, and is actually confirmed by four peaks at the higher mass end of the spectrum (243.084: IND + H+; 254.078: 2IND + H+ + Na+ (2 + ion); 265.064: IND + Na+; 287.046: IND − H+ + 2Na+). Signals attributable to isonicotinic amide INM are missing from the spectrum.
 | ||
| Fig. 3 ESI-MS spectrum of the product mixture at isoniazid excess. The peak marked with * is a known instrument background peak that does not belong to the sample. | ||
Further investigation of the products was carried out by 1H-NMR spectroscopy. Some of the results are shown in the ESI as Fig. S7.† The 1H-NMR spectrum of isoniazid in D2O in basic medium shows two doublets: the first at 7.56 ppm, the second at 8.40 ppm. When an excess of NaOCl is added, the structure of the spectrum remains the same, but the doublets appear at 8.42 ppm and 8.90 ppm and the coupling constant increases. When solid isonicotinic acid is added to this sample, no new peaks appear in the spectrum. Therefore, isonicotinic acid is the sole organic product of the oxidation at an excess of hypochlorite ion, which agrees well with the results of the spectrophotometric titration.
In summary, when hypochlorite ion is used in excess, isoniazid is oxidized only to isonicotinic acid. At isoniazid excess, a mixture of isonicotinic acid and the coupled molecule IND is formed. It should be added that the relative amount of IND seems to be dependent on the conditions. A higher absolute concentration of isoniazid seems to favor the formation of IND. Unfortunately, kinetic studies were not feasible in the region where IND is a significant product as the formation of nitrogen bubbles interfered with the spectrophotometric detection.
Detailed kinetics
The kinetics of the process was studied by stopped-flow spectrophotometry. It was not usually possible to use one of the reagents in high excess because of bubble formation as mentioned earlier. In addition, using a high excess of one of the reagents would have resulted in high reaction rates on the limit of measurability by the stopped-flow method. Therefore, the concentration range of the kinetic studies was limited to conditions where the concentrations of the initial reagents were not very far from stoichiometric. Some sample curves are shown in Fig. 4, these demonstrate the effect of changing hydroxide ion concentration on the detected kinetic curves.As pseudo-first order conditions could not be applied, the evaluation was based on determining the initial rate50,51 of absorbance change at 320 nm. This wavelength proved to be selective to isoniazid under the experimental conditions used in this work. The dependence of initial rates on the concentration of isoniazid is shown in Fig. 5 at two different pH values. In both cases, the points define a reasonably good straight line without an intercept. It follows that the process is first-order with respect to the organic reactant. A similar concentration dependence for hypochlorite ion is shown in Fig. 6. Again, the rates are directly proportional to [OCl−] at both hydroxide ion concentrations. These observations prove that the order of the reaction is 1 with respect to both reagents and the overall rate law is second order:
| v = kapp[INH][OCl−] | (5) |
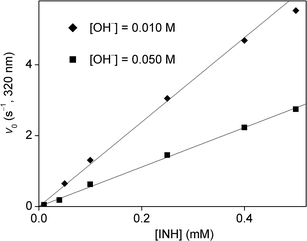 | ||
| Fig. 5 Initial rate as a function of isoniazid concentration in the oxidation of isoniazid with hypochlorite ion. [OCl−] = 1.0 mM, T = 25.0 °C, l = 1.00 cm. | ||
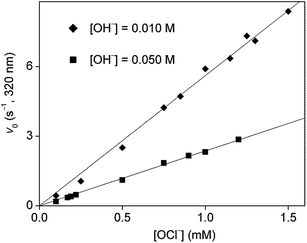 | ||
| Fig. 6 Initial rate as a function of hypochlorite ion concentration in the oxidation of isoniazid with hypochlorite ion. [INH] = 0.50 mM, T = 25.0 °C, l = 1.00 cm. | ||
In this equation, kapp is a pH-dependent apparent rate constant that also incorporates the molar absorptivity of isoniazid because v is defined as the initial rate of absorbance change. It should be emphasized that [INH] here means the total concentration of all different protonated forms of isoniazid.
The effect of chloride ion was also tested as it is a product of the reaction. As shown in Fig. S8 of the ESI,† addition of Cl− prior to initiating the reaction does not have any effect on the initial rate and does not influence the kinetic curves, either. This clearly confirms the expectations, as chloride ion usually only has effects on the reactions of hypochlorous acid in acidic medium, where the equilibria involving the formation of chlorine (Cl2) are relevant.23–25,41
As shown in Fig. 4, a change in the concentration of hydroxide ion strongly influences the shape of the detected traces. As [OH−] increases, the initial absorbance of the kinetic curves increases, but the initial rate of absorbance change decreases. These two phenomena can be interpreted by a single acid–base equilibrium. In addition, it is also to be noted that the final absorbance does not decrease to zero. The pH-dependence of the final absorbance was essentially the same as the pH dependence of the initial absorbance, so the final absorbance reflects that some unreacted isoniazid remains after reaction. The initial ratio of reactants was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (INH
2 (INH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OCl−), so this observation gives some support to the assumption that the experimentally determined stoichiometry (0.46 INH
OCl−), so this observation gives some support to the assumption that the experimentally determined stoichiometry (0.46 INH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) OCl−) is somewhat different from that shown in eqn (1).
OCl−) is somewhat different from that shown in eqn (1).
The change in the initial absorbance values is a consequence of a reaction that occurs within the dead time of the stopped-flow instrument (about 1 ms). This is clearly not the redox reaction, which is slower. It was also shown that the spectrum of isoniazid (without the addition of any oxidant) depends on the pH in this range (Fig. S9 in the ESI†). Isoniazid is known to take part in two distinct acid–base equilibria in the measurable pH range (2.0–12.0).52 The first equilibrium (i.e. the one with the lowest pK) corresponds to the protonation of the pyridine moiety and is characterized by a pK of 3.53 at 25.0 °C in aqueous solution containing 20% of methanol.52 Thus, this protolytic step is only significant in the acidic pH range. The second step is a deprotonation of the amidic nitrogen of isoniazid, and is characterized by the following equilibrium:
| IN–CONHNH2 = IN–CON−NH2 + H+ | (6) |
The corresponding acid dissociation constant is defined as follows:
 | (7) |
It should be pointed out that the notation [IN–CONHNH2] was introduced here to mark the concentration of the neutral form of isoniazid, in contrast with [INH], which means the total concentration of all protonated forms. The literature value of the pK is 11.14,52 which is within our investigated pH range. Therefore, the acid–base equilibrium shown in eqn (6) could be responsible for the observations. The forms IN–CONHNH2 and IN–CON−NH2 have different spectra, this causes the pH-dependence of the initial absorbance values. Using standard considerations, the following formula can be derived for the initial absorbance:
 | (8) |
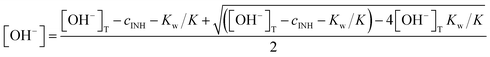 | (9) |
The dependence of the initial absorbance on [OH−]T (where [OH−]T is the analytical concentration of sodium hydroxide) is shown in Fig. 7. The value of pKw, the ionic product of water, was fixed at 13.77, which is the literature value for 1.0 M NaClO4 medium.53 In the initial attempts to fit the experimental data, AlowpH was found to be very close to zero and its standard deviation was larger than the fitted value. It was concluded that AlowpH is not a significant term and its value was fixed at zero. The remaining two parameters were estimated by least squares fitting as follows: AhighpH = 1.87 ± 0.02 and pK = 11.16 ± 0.03. The results show that the form IN–CON−NH2 absorbs strongly, but IN–CONHNH2 does not have significant absorption at the measurement wavelength (320 nm). The fitted pK is in excellent agreement with the literature value of 11.14 despite the fact that the two values were determined in slightly different media.
 | ||
| Fig. 7 Initial absorbance as a function of pH in the oxidation of isoniazid with hypochlorite ion. [INH] = 0.50 mM, [OCl−] = 1.0 mM, T = 25.0 °C, l = 1.00 cm. | ||
The pH-dependence of the initial rate can be interpreted by considering two different factors. First, the apparent molar absorbance of isoniazid changes as a result of equilibrium 6. A simple way to correct for this effect is to divide the initial rate by the initial absorbance. Second, the rate of isoniazid consumption changes with shifting pH as the reactivities of the two different forms are not the same. The usual derivation, which is based on considering reaction 6 as a pre-equilibrium, gives the following results:
 | (10) |
In this formula, rlowpH is characteristic of the reaction of the IN–CON−NH2 form, whereas rhighpH belongs to the IN–CON−NH− form. Fig. 8 shows the a plot of v0/At=0 as a function of [OH−]T (see eqn (9) and (10) regarding the calculation of [OH−]). The first attempts at fitting gave very low values for rhighpH, which were again smaller than the estimated standard deviation. Therefore, the contribution of this term to the overall rate is never significant and its value was fixed at zero in the final evaluation. The other two parameters were estimated as follows: rlowpH = 29.4 ± 1.4 s−1 and pK = 11.00 ± 0.04 (using 13.77 as pKw again53). The estimated pK is in acceptable agreement with the one estimated from the initial absorbances and also with the literature value.
 | ||
| Fig. 8 Absorbance-corrected initial rate as a function of pH in the oxidation of isoniazid with hypochlorite ion. [INH] = 0.50 mM, [OCl−] = 1.0 mM, T = 25.0 °C, l = 1.00 cm. | ||
These results imply that hypochlorite ion only reacts with the neutral form of isoniazid. The rate determining step is a simple second order process:
 | (11) |
The value of the bimolecular rate constant (k) can be calculated from the initial rate of absorbance change at 320 nm (v0) from any of the experiments using the following formula:
 | (12) |
Based on the total kinetic data set, k = (3.4 ± 0.7) × 104 M−1 s−1 was estimated. The detailed calculations are given in Table S1 of the ESI.†
At this point, it should be noted that all of the previous results were derived from measuring initial rates. For a complete kinetic description, it needs to be proved that the rate equation obtained in this way is suitable for describing the full kinetic traces. The kinetic curves of the overall second order process between reactants R1 and R2 under non-flooding conditions can be described as follows:50,51
 | (13) |
When the initial ratio of the reactants is exactly stoichiometric ([R1]0 = [R2]0/μ), the time dependence of the concentration of R1 is given as follows:50,51
 | (14) |
For any other initial conditions, the formula can be given as:
 | (15) |
The absorbance can be calculated from Beer's law using εR1, εR2 and εPi for the molar absorptivities of R1, R2 and products Pi, in order:
| A = εR1[R1] + εR2[R2] + ΣεPi[Pi] | (16) |
The time dependence of the absorbance for the case described by eqn (14) is therefore:
 | (17) |
The parameters P1, P2 and P3 are related to the other quantities through the following equations:
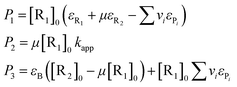 | (18) |
When one of the two reactants is in excess (i.e. eqn (15) is valid), the following formula is valid for the absorbance:50,51
 | (19) |
P1, P2, P3 and P4 are parameters in these equations that are related to the initial concentration of the reactants and the molar absorptivities of the reactants and products as follows:
 | (20) |
For the measurements where the initial hydroxide ion concentration was high enough (≥10 mM) to be practically constant throughout the entire experiment, these equations were used to fit the full kinetic traces measured. As shown by Fig. 9 and Fig. S10 in the ESI,† the fits were excellent. Some of the numerical results of these fittings are also displayed in the ESI as Table S2.† The excellent fit of these integrated expression shows that the rate equation established based on the initial rates describes the entire studied process, no secondary reactions emerge at longer reaction times. However, these integrated expressions can only be used for curves for which the initial hydroxide ion concentration is at least 10 mM, otherwise [OH−] also changes significantly during the process, and the full integration of rate law (cf. eqn (10)) is not possible analytically any more.
 | ||
| Fig. 9 Example of fitting experimental data to eqn (19). [INH] = 0.50 mM, [OCl−] = 1.15 mM, [OH−]T = 100 mM, T = 25.0 °C, l = 1.00 cm. The grey line represent the fitted curve. The letter A represents absorbance. | ||
Conclusion
This work has shown that hypochlorite ion reacts quite rapidly with the tuberculosis drug isoniazid. The stoichiometry of the reaction shows some variation depending on the identity of the excess reagent. The organic products formed are isonicotinic acid and 2-(4-pyridinylcarbonyl)hydrazide, a molecule that can be formally derived by the condensation of one molecule of isoniazid with one molecule of isonicotinic acid. The rate determining step is always the direct bimolecular reaction between hypochlorite ion with the neutral form of isoniazid. Deprotonated isoniazid does not react at significant rate with hypochlorite ion. As the HOCl/OCl− system plays an important role in fighting bacterial infections in the body. The pK of hypochlorous acid is 7.40,23 thus, the pathway identified in this work must be taken into consideration when the metabolism and efficiency of isoniazid is evaluated in biological systems on a molecular basis. Because the oxidation of the hydrazide group is very fast and can also be made very selective by the proper choice of conditions, the oxidation of hydrazides by hypochlorite ion may also be useful in organic synthesis.Acknowledgements
Ms. Mária Szabó is acknowledged for her help to prepare the NaOCl stock solution and determining its concentration. The authors thank the Hungarian Science Foundation for financial support under grant No. NK 105156. The research was supported by the EU and co-financed by the European Social Fund under the project ENVIKUT (TÁMOP-4.2.2.A-11/1/KONV-2012-0043).References
- Global tuberculosis report 2014, World Health Organization, freely available from the following website: http://www.who.int/tb/publications/global_report/en/.
- H. Lw and F. Io, Am. Rev. Tuberc., 1957, 75, 670–674 Search PubMed.
- M. R. Juchau and A. Horita, Drug Metab. Rev., 1972, 1, 71–100 CrossRef.
- S. D. Nelson, T. J. Mitchell, W. R. Snodgrass and G. B. Corcoran, Science, 1976, 193, 901–903 CAS.
- H. A. Shoeb, B. U. Bowman Jr, A. C. Ottolenghi and A. J. Merola, Antimicrob. Agents Chemother., 1985, 27, 399–403 CrossRef CAS.
- Y. Zhang, B. Heym, B. Allen, D. Young and S. Cole, Nature, 1992, 358, 591–593 CrossRef CAS PubMed.
- K. Johnsson and P. G. Schultz, J. Am. Chem. Soc., 1994, 116, 7425–7426 CrossRef CAS.
- R. S. Magliozzo and J. A. Marcinkeviciene, J. Am. Chem. Soc., 1996, 118, 11303–11304 CrossRef CAS.
- R. F. Zabinski and J. S. Blanchard, J. Am. Chem. Soc., 1997, 119, 2331–2332 CrossRef CAS.
- J. Y. Wang, R. M. Burger and K. Drlica, Antimicrob. Agents Chemother., 1998, 42, 709–711 CAS.
- R. Pierattelli, L. Banci, N. A. J. Eady, J. Bodigue, J. N. Jones, P. C. E. Moody, E. L. Raven, B. Jamart-Grégoire and K. A. Brown, J. Biol. Chem., 2004, 279, 39000–39009 CrossRef CAS PubMed.
- B. Wiseman, X. Carpena, M. Feliz, L. J. Donald, M. Pons, I. Fita and P. C. Loewen, J. Biol. Chem., 2010, 285, 26662–26673 CrossRef CAS PubMed.
- L. V. Forbes, P. G. Furtmüller, I. Khalilova, R. Turner, C. Obinger and A. J. Kettle, Biochem. Pharmacol., 2012, 84, 949–960 CrossRef CAS PubMed.
- P. R. Martins, L. M. C. Ferreira, K. Araki and L. Angnes, Sens. Actuators, B, 2014, 192, 601–606 CrossRef CAS PubMed.
- S. Saikolappan, K. Das and S. Dhandayuthapani, J. Bacteriol., 2015, 197, 51–62 CrossRef CAS PubMed.
- X. Meng, J. L. Maggs, T. Usui, P. Whitaker, N. S. French, D. J. Naisbitt and B. K. Park, Chem. Res. Toxicol., 2015, 28, 51–58 CrossRef CAS PubMed.
- J. E. Harrison and J. Schultz, J. Biol. Chem., 1976, 251, 1371–1374 CAS.
- B. W. Griffin and R. Haddox, Arch. Biochem. Biophys., 1985, 239, 305–309 CrossRef CAS.
- M. B. Hampton, A. J. Kettle and C. C. Winterbourn, Blood, 1988, 92, 3007–3017 Search PubMed.
- D. I. Pattison and M. J. Davies, Chem. Res. Toxicol., 2001, 14, 1453–1464 CrossRef CAS PubMed.
- C. L. Hawkins, D. I. Pattison and M. J. Davies, Amino Acids, 2003, 25, 259–274 CrossRef CAS PubMed.
- M. J. Davies, C. L. Hawkins, D. I. Pattison and M. D. Rees, Antioxid. Redox Signaling, 2008, 10, 1199–1234 CrossRef CAS PubMed.
- M. Galajda, T. Fodor, M. Purgel and I. Fábián, RSC Adv., 2015, 5, 10512–10520 RSC.
- M. Szabó, Z. Baranyai, L. Somsák and I. Fábián, Chem. Res. Toxicol., 2015, 28, 1282–1291 CrossRef PubMed.
- L. C. Adam, I. Fábián, K. Suzuki and G. Gordon, Inorg. Chem., 1992, 31, 3534–3541 CrossRef CAS.
- W. Yu, L. Campos, T. Shi, G. Li and N. Graham, RSC Adv., 2015, 5, 27970–27977 RSC.
- M. Deborde and U. von Gunten, Water Res., 2008, 42, 13–51 CrossRef CAS PubMed.
- G. C. White, Handbook of Chlorination and Alternative Disinfectants, Van Nostrand Reinhold, New York, 1992 Search PubMed.
- J. Huang, C. Zhang and Z. Zhang, Fresenius. J. Anal. Chem., 1999, 363, 126–128 CrossRef CAS.
- R. Zhao, Y. Tang, S. Wei, X. Xu, X. Shi and G. Zhang, React. Kinet., Mech. Catal., 2012, 106, 37–47 CrossRef CAS.
- J. Zha, B. Fu, C. Qin, L. Zeng and X. Hu, RSC Adv., 2014, 4, 43110–43113 RSC.
- Y. Wolman, P. M. Gallop, A. Patchornik and A. Berger, J. Am. Chem. Soc., 1962, 84, 1889–1892 CrossRef CAS.
- J. B. Aylward and R. O. C. Norman, J. Chem. Soc. C, 1968, 2399–2402 RSC.
- J. Tsuji, T. Nagashima, N. T. Qui and H. Takayanagi, Tetrahedron, 1980, 36, 1311–1315 CrossRef CAS.
- S. W. McCombie, S. I. Lin and S. F. Vice, Tetrahedron Lett., 1990, 40, 8767–8770 CrossRef.
- P. G. M. Wuts and M. P. Goble, Org. Lett., 2000, 2, 2139–2140 CrossRef CAS PubMed.
- R. I. J. Amos, B. S. Gourlay, C. H. Schiesser, J. A. Smith and B. F. Yates, Chem. Commun., 2008, 1695–1697 RSC.
- K. A. Rickman, K. L. Swancutt, S. P. Mezyk and J. J. Kiddle, Bioorg. Med. Chem. Lett., 2013, 23, 3096–3100 CrossRef CAS PubMed.
- H. Ramalingaiah and M. K. Puttaswamy, Indian J. Chem., Sect. A: Inorg., Bio-inorg., Phys., Theor. Anal. Chem., 2001, 40, 110–114 Search PubMed.
- D. Amin and A. M. Al-Daher, Microchem. J., 1982, 27, 389–392 CrossRef CAS.
- G. Peintler, I. Nagypál and I. R. Epstein, J. Phys. Chem., 1990, 94, 2954–2958 CrossRef CAS.
- G. Gordon and P. H. Tewari, J. Phys. Chem., 1966, 70, 200–204 CrossRef CAS.
- I. Fábián and G. Lente, Pure Appl. Chem., 2010, 82, 1957–1973 CrossRef.
- M. Gombár, É. Józsa, M. Braun and K. Ősz, Photochem. Photobiol. Sci., 2012, 11, 1592–1595 Search PubMed.
- T. Lehóczki, É. Józsa and K. Ősz, J. Photochem. Photobiol., A, 2013, 251, 63–68 CrossRef PubMed.
- B. Tonomura, H. Nakatani, M. Ohnishi, J. Yamaguchi-Ito and K. Hiromi, Anal. Biochem., 1978, 84, 370–383 CrossRef CAS.
- G. Peintler, A. Nagy, A. K. Horváth, T. Körtvélyesi and I. Nagypál, Phys. Chem. Chem. Phys., 2000, 2, 2575–2586 RSC.
- M. T. Beck and I. Nagypál, Chemistry of Complex Equilibria, Ellis Horwood Ltd, Chichester, 1990, pp. 109–126 Search PubMed.
- W. Fifield and D. Kealey, Principles and Practice of Analytical Chemistry, Blackie Academic & Professional, Glasgow, 4th edn, 1995, pp. 371–372 Search PubMed.
- G. Lente, Deterministic Kinetics in Chemistry and Systems Biology, Springer, New York, 2015 Search PubMed.
- J. H. Espenson, Chemical kinetics and reaction mechanisms, McGraw-Hill, New York, USA, 2nd edn, 1995 Search PubMed.
- C. Raàfols, E. Bosch, R. Ruiz, K. J. Box, M. Reis, C. Ventura, S. Santos, M. E. Araújo and F. Martins, J. Chem. Eng. Data, 2012, 57, 330–338 CrossRef.
- T. Vilarifio and M. E. Sastre de Vicente, J. Solution Chem., 1997, 26, 833–846 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Figures referred to in the main text of the article. See DOI: 10.1039/c5ra13540k |
| This journal is © The Royal Society of Chemistry 2015 |