Two-dimensional correlation infrared spectroscopy reveals the detailed molecular movements during the crystallization of poly(ethylene-co-vinyl alcohol)†
Gehong Su,
Tao Zhou*,
Xifei Liu,
Jihai Zhang,
Jianjun Bao* and
Aiming Zhang
State Key Laboratory of Polymer Materials Engineering of China, Polymer Research Institute, Sichuan University, Chengdu 610065, China. E-mail: zhoutaopoly@scu.edu.cn; jjbao2000@sina.com; Fax: +86-28-85402465; Tel: +86-28-85402601
First published on 22nd September 2015
Abstract
In this paper, quantitative spectroscopic evidence for the important role of hydrogen bonds during the cooling crystallization of poly(ethylene-co-vinyl alcohol) (EVOH) was successfully obtained. Furthermore, the detailed molecular movements during the crystallization of EVOH were revealed via two-dimensional correlation infrared spectroscopy. Two cooling crystallization processes were detected at 159 °C and around 101–105 °C via the combination of DSC and the newly proposed scaling-MW2D correlation FTIR spectroscopy. These two crystallization processes were defined as the primary crystallization (region I) and the secondary perfection process (region II) of EVOH. The methods for calculating the enthalpies of the pair-bonded hydrogen bonding (ΔHh), vinyl alcohol (VA) repeating unit crystallization (ΔHC-VA), VA repeating unit diffusion into the crystal lattice (ΔHl-VA), and ethylene (ET) repeating unit crystallization (ΔHC-ET) were established via van ’t Hoff plots. For regions I and II, the contributions of the pair-bonded hydrogen bonding of the VA repeating units to the entire EVOH crystallization were 42.8% (ΔHh = −90.4 ± 5.2 kJ mol−1) and 64.6% (ΔHh = −75.8 ± 3.1 kJ mol−1), respectively. However, the contributions of the ET crystallization to the EVOH crystallization were 19.4% (ΔHC-ET = −41.0 ± 2.0 kJ mol−1) and 32.7% (ΔHC-ET = −38.3 ± 0.8 kJ mol−1), which were only half of the contributions of the pair-bonded hydrogen bonding. 2D correlation analysis was used to investigate the sequential order of the groups’ movement in the crystallization. It was found that region I had 3 steps. The first step is the formation of the hydrogen bonds in the VA repeating unit, and the second step is the diffusion of the VA repeating unit into the crystal lattice, resulting in the primary crystallization. The third step is the ET repeating unit crystallization accompanied by the movement of the VA repeating unit without hydrogen bonding in the amorphous region. Region II had 4 steps. The first step is also the generation of the hydrogen bonds in the VA repeating unit. The second step is a local rearrangement of the lattice in the imperfect crystalline of the VA repeating unit, called the secondary perfection process. The third step is the movement of the VA repeating unit without hydrogen bonding in the amorphous region. The fourth step is the weak crystallization of the ET repeating unit at a low temperature.
1. Introduction
The poly(ethylene-co-vinyl alcohol) (EVOH) random copolymer is a semicrystalline material with an excellent gas-barrier property that has been widely applied to various industry fields, such as food packaging, plastic containers, and gasoline tanks.1–8 Recently, EVOH has attracted plenty of research interest in the fields of water treatment and biomedical science due to its hydrophilicity and good blood compatibility.9,10 The EVOH copolymers are commonly synthesized via a saponification reaction from an ethylene-co-vinyl acetate copolymer, and the chains of the EVOH copolymers are constructed by a random sequence of ethylene (ET) and vinyl alcohol (VA) monomeric units.11,12 The gas-barrier properties of EVOH are largely dependent upon the content of ethylene, and normally, the gas-barrier properties decrease with the increase of ethylene. EVOH copolymers with different comonomer content are easy to crystallize; the degree of crystallinity usually reaches 70%, and the properties also change a lot with the composition alone .3,13–16 EVOH copolymers show excellent gas-barrier performance due to the formation of a large amount of intra- and intermolecular hydrogen bonds via the hydroxyl groups on the VA segments.3,17 These hydrogen bonds also strongly enhance the interchain cohesion, and decrease the free volume of EVOH, resulting in the diffusion of the small gas molecules through the polymer matrix being very difficult.18–21In the past few decades, the crystallization behavior of EVOH copolymers has been extensively studied. It was proved that EVOH could form two types of crystals upon cooling from melts. These crystal types are orthorhombic and monoclinic when the content of VA comonomer is 0–40 mol% and 40–60 mol%, respectively.13,14 Cerrada reported that the orthorhombic crystal was generated for slowly crystallized samples.15 Lopez-Rubio investigated the influence of the cooling rate on the crystalline morphology of EVOH, and the formation of the orthorhombic crystal was also discovered at a high cooling speed.16 The orthorhombic crystal had a tendency to transform into the monoclinic crystal after an annealing treatment.16 It was reported that both ET and VA segments were incorporated into the crystal lattice during the crystallization process of EVOH, forming a mixed crystal. However, the capacity of the ET and VA segments diffusing into the lattice was different.13–16 The hydrogen bonds generated by the hydroxyl groups of the VA segments play an important role in the various properties of EVOH. Certainly, the crystallization behavior of EVOH is strongly influenced by the hydrogen bonds. However, the role of the hydrogen bonding in the crystallization process of EVOH has been unclear so far. Furthermore, quantitative evidence for the role of hydrogen bonding during EVOH crystallization is still lacking. So, an in depth understanding of the hydrogen bonding during EVOH crystallization will have great scientific and practical value.
Generalized two-dimensional (2D) correlation infrared spectroscopy was originally proposed by Noda in 1993,22 and has become a very important spectroscopy method. Due to the spreading of the spectral peaks over the second dimension, the spectral resolution of this method is significantly enhanced compared with 1D FTIR spectra.23 Thus, 2D correlation spectra can capture the information which is not obvious or is overlapping in the 1D spectra. In addition, the sequential order of the spectral variables can be easily obtained from the 2D correlation infrared spectra according to Noda’s rules. So, 2D correlation infrared spectroscopy can be conveniently used to investigate the detailed mechanism of a material’s transitions. In 2000, Thomas and Richardson proposed moving-window two-dimensional correlation spectroscopy (MW2D),24 which can be used to determine the transition temperature of a thermotropic liquid-crystal sample. MW2D can be directly applied to see the spectral correlation variation along both perturbation variable (e.g., temperature) and spectral variable (e.g., wavenumber) axes. After that, a similar method based on MW2D was proposed by Morita in 2006, which is called perturbation-correlation moving-window two-dimensional correlation spectroscopy (PCMW2D).25 Recently, we have proposed scaling moving-window two-dimensional correlation spectroscopy (scaling-MW2D), which was designed to identify weak transitions of materials.26 The reason we established scaling-MW2D is that conventional MW2D (by Thomas and Richardson)24 is unable to clearly distinguish weak transitions because of its low resolving capacity along the perturbation variable axis (e.g. temperature) in the MW2D spectra.26 For scaling-MW2D, the concept of a scaling factor α is provided.26 People can highlight interesting weak transitions by altering this scaling factor.
2D correlation infrared spectroscopy has an inherent advantage in the study of polymer transitions, especially the transitions in which hydrogen bonds are involved.27–36 In the past five years, scientists found that the best implementation is the combination of 2D correlation infrared spectroscopy with moving-window and generalized 2D correlation analysis.32,37–42 Generally speaking, MW2D or PCMW2D was first employed to determine the transition point and the transition region of polymers; then, generalized 2D analysis was performed to study the sequential order of the functional groups at a given transition.32,37–42 Many successful applications were reported in the study of the mechanism of physical or chemical polymer transitions.
In the present study, two regions of EVOH crystallization are determined via the combination of differential scanning calorimetry (DSC) and scaling-MW2D correlation FTIR spectroscopy. In addition, the methods for calculating the enthalpies of the pair-bonded hydrogen bonding (ΔHh), VA repeating unit crystallization (ΔHC-VA), and ET repeating unit crystallization (ΔHC-ET) are established via van ’t Hoff plots. Also, the relationship between the enthalpies of the EVOH crystallization (ΔHC-EVOH), ΔHC-ET, ΔHh, and the diffusion of the VA repeating unit into the crystal lattice (ΔHl-VA) is proposed. So, the contribution of the pair-bonded hydrogen bonding to the EVOH crystallization can be estimated quantitatively. Powerful 2D correlation analysis is used to investigate the sequential order of the movement of the groups involved in the crystallization process of EVOH. All the results from this paper confirm that the two regions of the EVOH crystallization are both dominated by the pair-bonded hydrogen bonding.
2. Experimental
2.1. Materials
EVOH was purchased from Nippon Synthetic Chemical Industry Co., Ltd with an ethylene content of 32 mol% (labeled as EVOHDC3203), and its melt index was 3.2 g/10 min (2.16 kg, 190 °C). The EVOH used here was designed for large-scale applications in packaging materials (such as packaging films), and has an outstanding processing performance and gas-barrier property.2.2. Sample preparation
The EVOH film used in the FTIR measurement was prepared by heat-pressing. Several EVOH particles of 1 g were first sandwiched between two polyethylene terephthalate (PET) sheets, and then were placed into a hot-press at 200 °C with a pressure of 20 MPa for 20 seconds. After that, the EVOH film samples were air cooled to room temperature. The thickness of the prepared film was approximately 10–20 μm. The EVOH film was finally cut into a circular shape (Φ 13 mm) using a cutter.2.3. DSC measurement
DSC measurements were carried out using a DSC 204 F3 (NETZSCH) with about 8 mg of the EVOH samples under a nitrogen atmosphere (25 ml min−1). The samples were initially heated from 30 °C to 225 °C at 20 °C min−1, and kept at 225 °C for 3 min to eliminate the thermal history. Subsequently, the samples were cooled down to 40 °C at 5 °C min−1, 10 °C min−1, and 20 °C min−1. After that, the samples stayed at 40 °C for 3 min, and finally were reheated again to 225 °C at 5 °C min−1, 10 °C min−1, and 20 °C min−1.2.4. In situ FTIR spectroscopy
A Nicolet iS10 Fourier transform spectrometer equipped with a deuterated triglycine sulfate (DTGS) detector was used for the FTIR experiments. Each FTIR spectrum was obtained from 20 scans with a resolution of 4 cm−1. The EVOH film prepared before was sandwiched between two KBr windows to prevent flow at a high temperature, and then was placed into a home-made in-situ pool (programmable heating and cooling device). The EVOH film was firstly heated from 30 °C to 230 °C at 5 °C min−1, and then kept at 225 °C for 3 min to eliminate the thermal history. The molten EVOH film was then cooled from 225 °C to 50 °C at 5 °C min−1. The temperature-dependent FTIR spectra were collected during the cooling process, and 119 spectra were gathered. During the FTIR experiment, the sample was protected by a dried high-purity nitrogen gas (200 ml min−1).2.5. Two-dimensional correlation analysis
Scaling-MW2D, MW2D, and generalized 2D correlation FTIR spectra were processed, calculated, and plotted by 2DCS software, developed by one of the authors. The window size of scaling-MW2D and MW2D was chosen as 11 (2m + 1) to produce high-quality spectra. Linear baseline corrections were applied in the region of 3660–2700 cm−1 and 780–700 cm−1 before analysis. The 3% correlation intensity of the spectra was regarded as noise and was cut off. In 2D correlation FTIR spectra, the pink areas represent positive correlation intensity, and the blue areas represent negative correlation intensity. The theory and algorithms for MW2D and generalized 2D correlation spectroscopy can be found in the literature.22–24,43 A brief introduction to the theory of scaling-MW2D based on auto-correlation is given below:A(v, I) is a M × N spectral intensity data matrix. I and v are the perturbation variable (e.g. temperature) and spectral variable (e.g. wavenumber), respectively.
 | (1) |
The reference spectrum and dynamic spectrum in the jth submatrix of A(v, I) are calculated according to eqn (2) and (3).
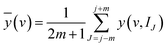 | (2) |
| ỹ(v, IJ) = y(v, IJ) − ȳ(v) | (3) |
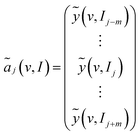 | (4) |
ãj(v, I) has 2m + 1 rows and this number is called the window size. The index range of the perturbation variable I of ãj(v, I) is from j − m to j + m. Then, the generalized synchronous 2D correlation spectra is calculated from ãj(v, I) according to eqn (5).
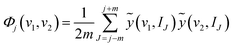 | (5) |
For each window, the standard deviations of the spectral intensities at v1 and v2 are defined in eqn (6) and (7).
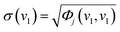 | (6) |
 | (7) |
The correlation coefficient ρ(v1, v2) is defined as follows:
| ρ(v1, v2) = Φj(v1, v2)/[σ(v1)σ(v2)] | (8) |
The scaled forms of the synchronous correlation spectrum in each window are defined as:
| Φj(v1, v2)(scaled) = Φj(v1, v2)[σ(v1)σ(v2)]−α|ρ(v1, v2)|β | (9) |
The constant α is called the scaling factor, and β is the correlation enhancement factor. The value of α is limited to 0–1.0. For scaling-MW2D based on auto-correlation, each row (ΩA,j (v, Ij)) of the correlation matrix of scaling-MW2D is directly extracted from a diagonal line (v1 = v2) of the Φj(scaled) matrix. The auto-correlation scaling-MW2D correlation spectrum is obtained through sliding the window position from j = 1 + m to M − m and repeating calculations of eqn (2)–(9) at each window.
Here, we also provide an easier way to obtain an auto-correlation scaling-MW2D spectrum. According to eqn (9), the auto-correlation scaling-MW2D can be described as follows.
| Φj(v1, v1)(scaled) = Φj(v1, v1)[σ(v1)σ(v1)]−α|ρ(v1, v1)|β | (10) |
| ρ(v1, v1) = Φj(v1, v1)/[σ(v1)σ(v1)] = 1 | (11) |
| Φj(v1, v1)(scaled) = [Φj(v1, v1)]1−α | (12) |
A conventional auto-correlation MW2D spectrum is obtained when the value of the scaling factor α = 0. In the present study, the value of α = 0.618 was chosen according to our previous study. The detailed theory and algorithm for scaling-MW2D can be found in ref. 26.
3. Results and discussion
3.1. DSC measurement
The DSC curves of EVOH upon cooling and reheating at 5 °C min−1, 10 °C min−1, and 20 °C min−1 are shown in Fig. 1. In Fig. 1(a), exothermic peaks are observed at 160 °C, 158 °C, and 151 °C when the cooling rates are 5 °C min−1, 10 °C min−1, and 20 °C min−1, respectively, which correspond to the maximum crystallization temperatures of EVOH at different cooling rates. The maximum crystallization temperature decreases as the cooling rate increases. It also can be observed that weak exothermic peaks appear when the temperature is within 80–120 °C (below the maximum crystallization temperature). An enlarged image of this range is also displayed in Fig. 1(a). These weak exothermic peaks are found at 106 °C, 104 °C, and 97 °C when the cooling rates are 5 °C min−1, 10 °C min−1, and 20 °C min−1, respectively. However, the peak at 106 °C with a cooling rate of 5 °C min−1 is more difficult to distinguish than the peaks at 104 °C (10 °C min−1) and 97 °C (20 °C min−1). Although the maximum crystallization temperatures of EVOH can be found in Fig. 1, the assignment of the weak exothermic peaks at 106 °C, 104 °C, and 97 °C are unclear. Fig. 1(b) illustrates the DSC curves upon reheating. The glass transition of EVOH can be easily determined at 59–61 °C, by the typical S-type shape. The melting point of EVOH is observed at 184–185 °C. The temperature of the glass transition of EVOH is obviously lower than that of the weak exothermic peaks found in Fig. 1(a).3.2. Temperature-dependent FTIR upon cooling
The temperature-dependent FTIR spectra of EVOH upon cooling from 225 °C to 50 °C in the regions of 3660–2700 cm−1 and 1160–700 cm−1 are illustrated in Fig. 2. For clarity, not all the spectra are displayed. The assignments of bands in Fig. 2 and the corresponding explanations are listed in Table 1.32,44–51 In Fig. 2(a), the bands at 3490 cm−1 are assigned to the O–H stretching of the “free” O–H groups in the vinyl alcohol repeating units of EVOH, and those at 3310 cm−1 are assigned to the O–H stretching of the hydrogen-bonded O–H groups in the VA repeating unit.44,45 The bands at 2932 cm−1 and 2854 cm−1 are attributed to the C–H asymmetrical stretching and symmetrical stretching of the –CH2– groups, respectively, in both the VA and ET repeating units.45,46 The bands at 2903 cm−1 are assigned to the C–H stretching of the –CH– groups in the VA repeating unit.45,46 It is clearly observed that the bands at 3490 cm−1 significantly move to 3310 cm−1 when the temperature decreases from 225 °C to 50 °C. Moreover, the intensity and the width of the bands at 3310 cm−1 obviously increases and broadens upon cooling. These features indicate the generation of hydrogen bonds in the VA repeating unit of EVOH. | ||
| Fig. 2 The temperature-dependent FTIR spectra of EVOH upon cooling from 225 °C to 50 °C. (a) 3660–2700 cm−1; (b) 1160–700 cm−1. | ||
| Wavenumber (cm−1) | Assignments | |
|---|---|---|
| Vinyl alcohol repeating unit (VA) | Ethylene repeating unit (ET) | |
| 3490 | v(O–H, free), O–H stretching of “free” O–H groups | — |
| 3310 | v(O–H, bonded), O–H stretching of hydrogen-bonded O–H groups | — |
| 2932 | vas(–CH2–), C–H asymmetrical stretching of –CH2– groups | vas(–CH2–) |
| 2903 | vs(–CH–), C–H stretching of –CH– groups | — |
| 2854 | vs(–CH2–), C–H symmetrical stretching of –CH2– groups | vs(–CH2–) |
| 1139 | vs(–C–O–, crystals), –C–O– stretching of the VA repeating unit in the crystals | — |
| 1100 | vs(–C–O–, amorphous), –C–O– stretching of the VA repeating unit in the amorphous region | — |
| 725 | — | γ(–CH2–, crystals), C–H rocking of –CH2– groups of the ET repeating unit in the crystals |
In Fig. 2(b), the bands at 1139 cm−1 and 1100 cm−1 are both assigned to the –C–O– stretching of the VA repeating unit.32,45,47–51 The 1139 cm−1 band is assigned to the –C–O– stretching in the crystals, and the band at 1100 cm−1 is attributed to the –C–O– stretching in the amorphous state.32,45,47–51 The bands at 725 cm−1 are assigned to the C–H rocking of the –CH2– groups of the ET repeating unit.45 Here, 1139 cm−1 and 725 cm−1 are the wavenumbers of the characteristic bands of the crystal in the VA and ET repeating units, respectively. The appearance and the intensity increase of the 1139 cm−1 band reveals the crystallization of the VA repeating unit of EVOH when the temperature decreases from 225 °C to 50 °C. At the same time, the intensity at 1100 cm−1 decreases, which represents the process of the amorphous state of the VA repeating unit transforming into the crystalline state. The enhancement of the intensity at 725 cm−1 also indicates the formation of the crystals of the ET repeating unit upon cooling. The temperature-dependent FTIR spectra of EVOH reveal not only the crystalline formation of both the VA and ET repeating unit, but also the generation of hydrogen bonds in the VA repeating unit upon cooling.
3.3. Crystallization regions of EVOH determined by scaling-MW2D FTIR
As shown in Fig. 3, the conventional MW2D FTIR spectra of EVOH upon cooling in the regions 3660–2700 cm−1, 1170–950 cm−1, and 780–700 cm−1 are first calculated. However, due to the great difficulty in detecting the weak transitions of polymers,26 only a transition at 159 °C is determined with conventional MW2D. This transition is the maximum crystallization temperature of EVOH, which has been observed in the DSC curves (Fig. 1). In the present study, the second derivative of the temperature-dependent FTIR spectra in the regions 3660–2700 cm−1 and 1160–700 cm−1 was also calculated according to the Savitzky–Golay method, and Omnic 8.1 software was used. As shown in Fig. S1 in the ESI,† the second derivative is helpful to distinguish the overlapping bands in the original FTIR spectra, and it also has some ability to detect small changes in absorbance along the wavenumber axis. However, such as in the temperature-dependent FTIR spectra, the second derivative has no capacity to determine the transition point and the transition regions along the temperature axis, not to mention to detect weak transitions. | ||
| Fig. 3 Conventional MW2D FTIR spectra of EVOH upon cooling in the regions 3660–2700 cm−1, 1170–950 cm−1, and 780–700 cm−1. | ||
Auto-correlation scaling-MW2D was then employed in our work, and the scaling-MW2D FTIR spectra of EVOH in the regions 3660–2700 cm−1, 1170–950 cm−1, and 780–700 cm−1 are shown in Fig. 4. As expected, the scaling-MW2D FTIR spectra detect two transitions at 159 °C and 101–105 °C. The former is the maximum crystallization temperature of EVOH, and the latter corresponds to the weak exothermic peak found in DSC (Fig. 1). In Fig. 4, correlation peaks appear at 1139 cm−1 and 725 cm−1 at a temperature of 101–105 °C. Because the bands at 1139 cm−1 and 725 cm−1 are the crystalline bands of EVOH, the transition at 101–105 °C is attributed to the secondary perfection process of EVOH. In the DSC measurement (Fig. 1), the weak peaks at around 97–106 °C are exothermic, which is also in line with one of the characteristics of crystallization. During the secondary perfection process, the temperature point of the band at 1139 cm−1 is 105 °C, which is 4 °C higher than that of the 725 cm−1 band (101 °C). This reveals that the secondary perfection process of the VA repeating unit is before that of the ET repeating unit. In the scaling-MW2D FTIR spectra, a large drift of the bands around 3310 cm−1 from 3350 cm−1 to 3260 cm−1 can also be observed when the temperature decreases from 216 °C to 60 °C. The crystallization process of EVOH determined by scaling-MW2D is consistent with that detected by DSC, and two regions are observed. The first region is at the maximum crystallization temperature at 159 °C, and the second region is the secondary perfection process at around 101–105 °C. As shown in Fig. 4, the temperature regions of these two crystallization processes can be determined to be within 170–145 °C (named as region I) and 112–85 °C (named as region II), respectively. It should be pointed out that these two processes are both continuous processes, and do not occur only at the transition temperature. That is to say, the crystallization processes are continuous within region I and region II. The transition points of 159 °C and 101–105 °C are the temperatures which have a maximum crystallization rate, and also correspond to the crystallization peaks observed in the DSC curves.
 | ||
| Fig. 4 Scaling-MW2D FTIR spectra of EVOH upon cooling in the regions 3660–2700 cm−1, 1170–950 cm−1, and 780–700 cm−1. The scaling factor is chosen as α = 0.618. | ||
The absorbance change extracted from the temperature-dependent FTIR spectra of EVOH at 3310 cm−1 and 1139 cm−1 from 225 °C to 50 °C upon cooling is illustrated in Fig. S2 in the ESI.† For 3310 cm−1, two sudden changes of absorbance around 159 °C and 103 °C can be clearly observed. These two temperatures are very close to the results determined by scaling-MW2D. The sudden change of absorbance around 159 °C is more obvious than that around 103 °C. The absorbance at 3310 cm−1 of both sudden changes is increased upon cooling, which shows the generation of hydrogen bonds in the VA repeating unit. For 1139 cm−1, a sudden change of absorbance around 159 °C is also observed. The increase of absorbance around 159 °C reveals the crystalline formation of the VA repeating unit. However, unlike at 3310 cm−1, no sudden change can be discerned around 103 °C. This is to say, the secondary perfection process cannot be distinguished from the absorbance change at 1139 cm−1. The absorbance change at 725 cm−1 upon cooling is also plotted in Fig. S3 in the ESI.†
3.4. Enthalpy of the generation of hydrogen bonds and the crystallization estimated from FTIR
The generation and breaking of hydrogen bonds of the VA repeating unit (represented by a band at 3310 cm−1) can be seen as an equilibrium reaction, considering that the hydrogen bond formation involved in the EVOH crystallization is pair-bonded.
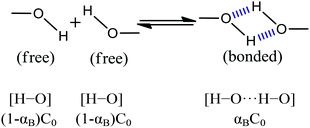 | (13) |
The relationship between absorbance A and the molar concentration C can be expressed by the Beer–Lambert law:52
| A = εLC | (14) |
At a lower temperature Tlow, the total concentration of the pair-bonded hydroxyl groups is C0. The concentration of the pair-bonded hydroxyl groups and free hydroxyl groups are CB and CF, respectively, at a higher temperature Thigh. The free hydroxyl groups can be gradually converted to the pair-bonded hydroxyl groups when the temperature decreases. So, the following relationship exists:
| CB + CF = C0 | (15) |
According to the Beer–Lambert law:52
| A0 = εBLC0 | (16) |
| AB = εBLCB | (17) |
| AF = εFLCF | (18) |
At a given temperature between Tlow and Thigh, the molar fraction of the pair-bonded hydroxyl groups is:
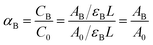 | (19) |
The mole fraction of the free hydroxyl groups can be expressed as:
 | (20) |
The equilibrium constant of eqn (13) can be calculated from:
 | (21) |
Eqn (21) can be transformed into the van ’t Hoff form:
 | (22) |
 | (23) |
So a straight line can be fitted from the plot between ln[αB/(1 − αB)2] and 1/T using least squares fitting. The enthalpy of the pair-bonded hydrogen bonding of the hydroxyl groups can be easily obtained from the slope of the fitted line.
Similarly, the crystallization enthalpy of the VA (represented by a band at 1139 cm−1) and ET repeating units (represented by a band at 725 cm−1) can also be calculated using a similar procedure, which is described in detail in the ESI.†
van ’t Hoff plots which are calculated from the temperature-dependent FTIR of EVOH are illustrated in Fig. 5. Three interesting bands were used to perform the van ’t Hoff analysis, including the absorbance changes at 3310 cm−1, 1139 cm−1, and 725 cm−1. The reason for choosing these bands is that the band at 3310 cm−1 is assigned to the hydrogen-bonded O–H groups in the VA repeating unit, and that at 1139 cm−1 is attributed to the –C–O– groups in the VA repeating unit in the crystal. Moreover, the band at 725 cm−1 is the crystalline characteristic band of the ET repeating unit. That is to say, the band at 3310 cm−1 represents the hydrogen bonding of the hydroxyl groups in the VA repeating unit, and those at 1139 cm−1 and 725 cm−1 represent the crystallization of the VA repeating unit and the ET repeating unit, respectively. Thus, the enthalpy of the hydrogen bond generation and that of the crystallization of EVOH upon cooling can be estimated via van ’t Hoff analysis. To obtain an accurate result, the absorbance change at 3310 cm−1 used in Fig. 5 was actually the change from 3350 cm−1 to 3260 cm−1. This is because of the observations of a large drift of the bands from 3350 cm−1 to 3260 cm−1 in the scaling-MW2D FTIR spectra (Fig. 4). Combining Fig. 4 and 5, as shown, two regions of 170–145 °C (region I) and 112–85 °C (region II) can be conveniently determined. According to the discussions of DSC and scaling-MW2D, region I and II can be confirmed as the primary crystallization process and the secondary perfection process, respectively.
In Fig. 5(a–c), it can be observed that four straight lines can be successfully fitted for each van ’t Hoff plot. This actually indicates that the enthalpy splits into 4 regions upon cooling. The estimated enthalpies of these 4 regions are listed in Table 2. The minus sign before the number reveals it is an exothermic process. So, a larger absolute value of the enthalpy represents a bigger trend to generate hydrogen bonds or the crystal. The enthalpy of the pair-bonded hydrogen bonding (ΔHh) is −32.8 ± 0.3 kJ mol−1 when the temperature is within 215–172 °C. This temperature is above the primary crystallization (region I), and EVOH is still in the melt state. At the same time, the crystallization enthalpy of the VA repeating unit (ΔHC-VA) is −5.3 ± 0.2 kJ mol−1. This reveals that a small number of hydrogen bonds in EVOH probably still exist at a high temperature. However, the crystallization is impossible due to there being no impetus at this high temperature. For region I, ΔHh = −90.4 ± 5.2 kJ mol−1 and ΔHC-VA = −170.1 ± 11.8 kJ mol−1, a great number of free hydroxyl groups form pair-bonded hydrogen bonds, and a strong crystallization occurs.
| 215–172 °C | Region I | 146–114 °C | Region II | |
|---|---|---|---|---|
| Enthalpy of the pair-bonded hydrogen bonding of the VA repeating unit, ΔHh (kJ mol−1) | −32.8 ± 0.3 | −90.4 ± 5.2 | −48.0 ± 0.6 | −75.8 ± 3.1 |
| Crystallization enthalpy of the VA repeating unit, ΔHC-VA (kJ mol−1) | −5.3 ± 0.2 | −170.1 ± 11.8 | −42.8 ± 1.2 | −72.6 ± 2.1 |
| Enthalpy of the VA repeating unit diffusing into the crystal lattice, ΔHl-VA (kJ mol−1) | — | −79.7 ± 6.6 | 5.2 ± 0.6 | 3.2 ± 1.0 |
| Crystallization enthalpy of the ET repeating unit, ΔHC-ET (kJ mol−1) | −9.4 ± 0.2 | −41.0 ± 2.0 | −20.6 ± 0.2 | −38.3 ± 0.8 |
| Crystallization enthalpy of the entire EVOH (kJ mol−1) | −14.7 ± 0.2 | −211.1 ± 6.9 | −63.4 ± 0.7 | −110.9 ± 1.5 |
| Contribution of the hydrogen bonding to VA crystallization (%) | — | 53.1 | — | 95.9 |
| Contribution of the hydrogen bonding to the whole EVOH crystallization (%) | — | 42.8 | — | 64.6 |
| Contribution of the VA repeating unit diffusing into the crystal lattice to the whole EVOH crystallization (%) | 37.8 | 2.7 | ||
| Contribution of the ET crystallization to the whole EVOH crystallization (%) | — | 19.4 | — | 32.7 |
| Contribution of the VA crystallization to the whole EVOH crystallization (%) | — | 80.6 (42.8 + 37.8) | — | 67.3 (64.6 + 2.7) |
| Total (%) | — | 100.0 (42.8 + 37.8 + 19.4) | — | 100.0 (64.6 + 2.7 + 32.7) |
It is noted that the absolute value of the calculated enthalpies is different from the usual reported data (10–40 kJ mol−1). As mentioned above, the formation of hydrogen bonds involved in the EVOH crystallization is pair-bonded, considering the regularity of the molecular chains in the crystal lattice. That is to say, a pair of hydroxyls produces two hydrogen bonds. Thus, the estimated enthalpies in our study actually include the enthalpies of formation of two hydrogen bonds in a pair of hydroxyls, and the enthalpy of formation of a single hydrogen bond is half of the calculated value, which is very close to that of the usual reported data.
The enthalpies estimated using the van ’t Hoff method in our work are close to those in other literature reports.53–56 In these reports, the van ’t Hoff method was also employed to estimate the enthalpy changes from the polymer repeating units, especially the enthalpy of the hydrogen bonds.
In the chemical structure of the VA repeating unit, the hydroxyl group and the ether bond are directly connected, namely as –C–O–H. In general, scientists believe that hydrogen bonding is the direct driving force leading to the crystallization of PVA or EVOH.13–15,32 That is to say, from the molecular structure, the crystal of the VA repeating unit (reflected by 1139 cm−1) certainly contains the stable pair-bonded hydrogen bonds of the hydroxyl groups. The generation of pair-bonded hydrogen bonds is an important part of the VA repeating unit crystallization. From the point of view of polymer physics, the polymer crystallization needs the molecular repeating unit to be able to smoothly diffuse into the crystal lattice. Thus, there exists the following relationship:
| ΔHC-VA ≈ ΔHh + ΔHl-VA | (24) |
Eqn (24) shows that both ΔHh and ΔHl-VA are essential parts of the crystallization enthalpy of the VA repeating unit (ΔHC-VA). It is noted that eqn (24) is only correct and reasonable when the temperature is below or equal to the initial crystallization temperature (onset point). In this study, this initial temperature is 170 °C.
For region I, ΔHl-VA = −79.7 ± 6.6 kJ mol−1 which shows that the VA repeating units of EVOH have a strong tendency to spontaneously form the crystal lattice under the induction of pair-bonded hydrogen bonding, accompanied by a large release of heat. After region I, ΔHh = −48.0 ± 0.6 kJ mol−1 and ΔHC-VA = −42.8 ± 1.2 kJ mol−1, and the capacity for forming pair-bonded hydrogen bonds is obviously reduced when the temperature is within 146–114 °C. The calculated ΔHl-VA is 5.2 ± 0.6 kJ mol−1, and this indicates that the VA repeating units never have a capacity to diffuse into the crystal lattice, also reflecting the loss of the molecular chains’ movement at a low temperature. In region II, ΔHh = −75.8 ± 3.1 kJ mol−1 and ΔHC-VA = −72.6 ± 2.1 kJ mol−1, and a number of pair-bonded hydrogen bonds are generated again from the free hydroxyl groups. This is probably because a low temperature is more conducive for the formation of pair-bonded hydrogen bonds from free hydroxyl groups. ΔHl-VA is calculated as 3.2 ± 1.0 kJ mol−1. For region II, a part of the molecular repeating unit gains the ability to move locally due to the bonding of pair-bonded hydrogen bonds, resulting in a local rearrangement of the lattice in the imperfect crystal. The VA repeating units absorb energy of 3.2 ± 1.0 kJ mol−1 from the enthalpy of the pair-bonded hydrogen bonding to obtain this local motion to recrystallize. From the view point of the released and absorbed enthalpy, the contribution of the pair-bonded hydrogen bonding to the VA crystallization in region I and II can be estimated as:
 | (25) |
As listed in Table 2, the contribution of the pair-bonded hydrogen bonding to the VA crystallization is 53.1% and 95.9% during the primary crystallization (region I) and the secondary perfection process (region II), respectively.
For the whole EVOH crystallization, it is important to note that there are contributions from both the crystallization of the ET and VA repeating units. Thus, the ET crystallization also needs to be focused on.
In Table 2, it can be seen that the crystallization enthalpy of the ET repeating unit (ΔHC-ET) is −9.4 ± 0.2 kJ mol−1 when the temperature is above region I (within 215–172 °C). This indicates that the crystallization of the ET repeating unit is impossible, which is similar to the VA repeating unit (ΔHC-VA = −5.3 ± 0.2 kJ mol−1). As is known, EVOH is in a molten state at such a high temperature, and therefore, the crystallization cannot occur. In region I, ΔHC-ET is −41.0 ± 2.0 kJ mol−1, and the ET repeating unit crystallization take places. However, the absolute value of ΔHC-ET is significantly less than that for the VA repeating unit (ΔHC-VA = −170.1 ± 11.8 kJ mol−1), and even obviously less than the enthalpy of pair-bonded hydrogen bonding of the VA repeating unit (ΔHh = −90.4 ± 5.2 kJ mol−1). This clearly shows that the crystallization trend of the ET repeating unit is much weaker than that of the VA repeating unit. Compared with the VA repeating unit, the ET repeating unit crystallization can only be called a weak crystallization. In region II, ΔHC-ET = −38.3 ± 0.8 kJ mol−1, and its absolute value is also obviously less than those of ΔHC-VA (−72.6 ± 2.1 kJ mol−1) and ΔHh (−75.8 ± 3.1 kJ mol−1). From the viewpoint of thermodynamics, this result also reveals that the crystallization trend of the VA repeating unit is much larger than that of the ET repeating unit. It is noted that ΔHC-ET is −20.6 ± 0.2 kJ mol−1 when the temperature is within 146–114 °C (below region I and above region II). The absolute value of this is even lower than that in region II (−38.3 ± 0.8 kJ mol−1), which reveals the enhancement in the crystallization ability of the ET repeating unit for some reason in region II. Overall, as with the VA repeating unit, the ET crystallization is an indispensable part of the whole EVOH crystallization.
The contribution of the pair-bonded hydrogen bonding, as well as the VA repeating unit diffusion into the crystal lattice, to the whole EVOH crystallization can be calculated according to the following equations:
 | (26) |
 | (27) |
Here, ΔHC-ET is the crystallization enthalpy of the ET repeating unit, and ΔHl-VA is the enthalpy of the VA repeating unit diffusion into the crystal lattice, and ΔHh represents the enthalpy of the pair-bonded hydrogen bonding of the VA repeating unit. The detailed deduction of the above two equations can be found in the ESI.†
Similarly, the contributions of the ET and VA repeating unit crystallization to the whole EVOH crystallization can also be calculated from eqn (28) and (29):
 | (28) |
| ContributionVA-to-EVOH = 100 − contributionET-to-EVOH | (29) |
For region I and region II, the contributions of the VA crystallization, the ET crystallization, and the pair-bonded hydrogen bonding to the whole EVOH crystallization are calculated. As listed in Table 2, in region I, the contribution of the VA crystallization to the whole EVOH crystallization is 80.6%; however, that of the ET repeating unit only reaches 19.4%. In region II, the contributions of the VA and ET crystallization are 67.3% and 32.7%, respectively. These results fully demonstrate that, in both regions I and II, the VA crystallization provides a larger contribution, and the ET crystallization provides a smaller contribution. Thus, EVOH crystallization is dominated by the VA repeating unit. In addition, the contributions of the hydrogen bonding to the VA crystallization in region I and region II are 53.1% and 95.9%, respectively. That is to say, the pair-bonded hydrogen bonding dominates the crystallization of the VA repeating unit. So, the important role of the pair-bonded hydrogen bonding in the whole EVOH crystallization is apparent. In Table 2, the contributions of the pair-bonded hydrogen bonding to the whole EVOH crystallization in regions I and II are 42.8% and 64.6%, which are obviously higher than those of the ET repeating unit (19.4% and 32.7%). The contribution of the pair-bonded hydrogen bonding to the whole EVOH crystallization is approximately twice that of the ET repeating unit.
3.5. Generalized 2D correlation analysis
To capture a detailed mechanism, as well as to understand the role of hydrogen bonding during the crystallization of the EVOH copolymer, the temperature-dependent FTIR spectra within region I (170–145 °C) and II (112–85 °C) were used to perform the generalized 2D correlation analysis. Generalized 2D FTIR spectra contain synchronous and asynchronous spectra. The sequential order of the spectral intensity changing at a given wavenumber can be conveniently probed by the sign of the correlation peaks using Noda’s rules. A simple summary of Noda’s rules is as follows:22(1) If Φ(v1, v2) > 0, Ψ(v1, v2) > 0 or Φ(v1, v2) < 0, Ψ(v1, v2) < 0, then the movement of v1 is before that of v2;
(2) If Φ(v1, v2) > 0, Ψ(v1, v2) < 0 or Φ(v1, v2) < 0, Ψ(v1, v2) > 0, then the movement of v1 is after that of v2;
(3) If Φ(v1, v2) > 0, Ψ(v1, v2) = 0 or Φ(v1, v2) < 0, Ψ(v1, v2) = 0, then the movements of v1 and v2 are simultaneous.
3.5.1.1. Sequential order of O–H groups and –C–O– groups in the VA repeating unit. The generalized 2D correlation FTIR spectra in the regions 3650–2990 cm−1, 3650–2990 cm−1 vs. 1170–950 cm−1, and 1170–950 cm−1 are shown in Fig. 6, which are calculated from the temperature-dependent spectra of region I (170–145 °C). Those on the left are the synchronous spectra, and those on the right are the asynchronous spectra. The pink areas and the blue areas represent the positive and the negative correlation intensity, respectively. The signs of the correlation peaks at 3490 cm−1, 3310 cm−1, 1139 cm−1, and 1100 cm−1 are summarized in Table 3. According to Noda’s rules, the sequential order is 3310 cm−1 → 1139 cm−1 → 1100 cm−1 = 3490 cm−1. In this study, the symbol “→” represents “before”, and “←” represents “after”. The corresponding sequential order of groups is v(O–H, bonded) → vs(–C–O–, crystals) → vs(–C–O–, amorphous) = v(O–H, free). This clearly shows that the first step of the primary crystallization of the VA repeating unit is the formation of hydrogen bonds, and then the second step of the diffusion of the VA repeating unit into the crystal lattice follows, resulting in the VA repeating unit crystallization. The third step is the movement of the VA repeating unit with no hydrogen bonds in the amorphous region. The sequential order gained from 2D correlation analysis is fully consistent with scientists’ previous assumption that the crystallization of EVOH was induced via the hydrogen bonding.13–15,32 As listed in Table 2, the estimated enthalpy of the pair-bonded hydrogen bonding ΔHh is −90.4 ± 5.2 kJ mol−1, and the contribution of the pair-bonded hydrogen bonding to the VA repeating unit crystallization is calculated as 53.1% within region I. All of these data reveal the important role of the hydrogen bonding on the primary crystallization of EVOH. Without the pair-bonded hydrogen bonding, the molecular chains of the VA repeating unit in EVOH will have no ability to smoothly diffuse into the crystal lattice and to maintain the stability of the lattice.
| Cross correlation peak (cm−1) | Sign in synchronous spectra | Sign in asynchronous spectra | Sequential order |
|---|---|---|---|
| (3490, 3310) | − | + | 3490 ← 3310 |
| (3490, 1100) | + | 0 | 3490 = 1100 |
| (3490, 1139) | − | + | 3490 ← 1139 |
| (3310, 1100) | − | − | 3310 → 1100 |
| (3310, 1139) | + | + | 3310 → 1139 |
| (1139, 1100) | − | − | 1139 → 1100 |
| 3310 cm−1 → 1139 cm−1 → 1100 cm−1 = 3490 cm−1 | |||
| (3490, 725) | − | 0 | 3490 = 725 |
| (3310, 725) | + | + | 3310 → 725 |
| (1139, 725) | + | + | 1139 → 725 |
| (1100, 725) | − | 0 | 1100 = 725 |
| 3310 cm−1 → 1139 cm−1 → 1100 cm−1 = 3490 cm−1 = 725 cm−1 | |||
| v(O–H, bonded) → vs(–C–O–, crystals) → vs(–C–O–, amorphous) = v(O–H, free) = γ(–CH2–, crystals) | |||
3.5.1.2. Sequential order of O–H groups and –C–O– groups in the VA repeating unit, and –CH2– groups in the ET repeating unit. EVOH contains both VA and ET repeating units. Thus, the sequential order among the representative groups of the VA and ET repeating units was also studied by 2D correlation analysis. Fig. 7 illustrates the generalized 2D correlation FTIR spectra in the regions 3650–2990 cm−1 vs. 780–700 cm−1 and 1170–950 cm−1 vs. 780–700 cm−1. The signs of the studied correlation peaks are also summarized in Table 3. The complete sequential order is 3310 cm−1 → 1139 cm−1 → 1100 cm−1 = 3490 cm−1 = 725 cm−1, namely, v(O–H, bonded) → vs(–C–O–, crystals) → vs(–C–O–, amorphous) = v(O–H, free) = γ(–CH2–, crystals). Region I contains a 3 step process. The results of the 2D correlation analysis reveal that the generation of the hydrogen bonds in the VA repeating unit is the key step in the primary crystallization of EVOH (159 °C). It is inferred that the movements between –CH2– groups in the ET repeating unit and –C–O–H groups in the VA repeating unit with no hydrogen bonds are simultaneous, which also indicates that the time taken for the ET repeating unit crystallization is the same as that for the VA repeating unit in the amorphous region. It can also be understood that the formation of the ET repeating unit crystal is accompanied by the movement of the VA repeating unit without hydrogen bonding in the amorphous region within region I.
3.5.2.1. Sequential order of O–H groups and –C–O– groups in the VA repeating unit. Fig. 8 shows the generalized 2D correlation FTIR spectra calculated from the temperature-dependent spectra of region II (112–85 °C) in the regions 3650–2990 cm−1, 3650–2990 cm−1 vs. 1170–950 cm−1, and 1170–950 cm−1. The signs of the correlation peaks are summarized in Table 4. The sequential order is 3310 cm−1 → 1139 cm−1 → 1100 cm−1 = 3490 cm−1, namely, v(O–H, bonded) → vs(–C–O–, crystals) → vs(–C–O–, amorphous) = v(O–H, free). This sequential order in region II is completely identical with that in region I. The first step of the secondary perfection process of the VA repeating unit is also the generation of hydrogen bonds. As listed in Table 2, the contribution of the pair-bonded hydrogen bonding to the VA repeating unit crystallization is 95.9% in region II, and the enthalpy of the pair-bonded hydrogen bonding ΔHh is −75.8 ± 3.1 kJ mol−1. The difference (of the second step in region II) with respect to region I is that this is a local rearrangement of the lattice in the imperfect crystal, called the secondary perfection process. The third step is the movement of the VA repeating unit with no hydrogen bonds in the amorphous region, which is also the same as that inferred from region I. These results disclose that the hydrogen bonding plays a leading role in the secondary perfection process of EVOH, which is more important than region I.
| Cross correlation peak (cm−1) | Sign in synchronous spectra | Sign in asynchronous spectra | Sequential order |
|---|---|---|---|
| (3490, 3310) | − | + | 3490 ← 3310 |
| (3490, 1100) | + | 0 | 3490 = 1100 |
| (3490, 1139) | − | + | 3490 ← 1139 |
| (3310, 1100) | − | − | 3310 → 1100 |
| (3310, 1139) | + | + | 3310 → 1139 |
| (1139, 1100) | − | − | 1139 → 1100 |
| 3310 cm−1 → 1139 cm−1 → 3490 cm−1 = 1100 cm−1 | |||
| (3490, 725) | − | − | 3490 → 725 |
| (3310, 725) | + | + | 3310 → 725 |
| (1139, 725) | + | + | 1139 → 725 |
| (1100, 725) | − | − | 1100 → 725 |
| 3310 cm−1 → 1139 cm−1 → 3490 cm−1 = 1100 cm−1 → 725 cm−1 | |||
| v(O–H, bonded) → vs(–C–O–, crystals) → vs(–C–O–, amorphous) = v(O–H, free) → γ(–CH2–, crystals) | |||
3.5.2.2. Sequential order of O–H groups and –C–O– groups in the VA repeating unit, and –CH2– groups in the ET repeating unit. Fig. 9 illustrates the generalized 2D correlation FTIR spectra in the regions 3650–2990 cm−1 vs. 780–700 cm−1 and 1170–950 cm−1 vs. 780–700 cm−1. The signs of the correlation peaks are also summarized in Table 4. The complete sequential order is 3310 cm−1 → 1139 cm−1 → 3490 cm−1 = 1100 cm−1 → 725 cm−1. The corresponding movements of groups is v(O–H, bonded) → vs(–C–O–, crystals) → vs(–C–O–, amorphous) = v(O–H, free) → γ(–CH2–, crystals). Obviously, the –CH2– of the ET repeating unit is the last group to move within region II, which also indicates that the secondary perfection process of the ET repeating unit is after that of the VA repeating unit. The sequential order of the –CH2– groups of the ET repeating unit is different from the findings in region I. This reveals the occurrence of a sub-process after the movement of the VA repeating unit. Thus, region II contains a 4 step process. The fourth step is probably due to the weak crystallization of the ET repeating unit at a low temperature. We can also infer that the movement of the ET repeating unit is a forced movement dominated by the VA repeating unit.
4. Conclusions
In this study, two regions of EVOH crystallization were detected via the combination of DSC curves and the newly proposed scaling-MW2D correlation FTIR spectroscopy. Region I was confirmed as the primary crystallization with the maximum crystallization temperature at 159 °C, and region II was confirmed as the secondary perfection process around 101–105 °C. Compared with the conventional MW2D, scaling-MW2D successfully distinguished region II, which appeared as a very weak transition of EVOH.The detailed steps in region I and region II inferred from the 2D correlation analysis are illustrated in Scheme 1. Region I is the primary crystallization of EVOH, which undergoes 3 steps. Region II is the secondary perfection process, which has 4 steps. In Scheme 1, the red balls represent the VA repeating unit of EVOH, and the black balls represent the ET repeating unit. The crystalline EVOH is represented by light blue areas, and gray areas are the amorphous region. For region I (170–145 °C), the first step is the formation of pair-bonded hydrogen bonds (ΔHh = −90.4 ± 5.2 kJ mol−1) in the VA repeating unit. The second step is the spontaneous diffusion of the VA repeating unit into the lattice to crystallize (ΔHl-VA = −79.7 ± 6.6 kJ mol−1). This step is induced by the first step (pair-bonded hydrogen bonding). The third step is the ET repeating unit crystallization (ΔHC-ET = −41.0 ± 2.0 kJ mol−1) accompanied by the movement of the VA repeating unit without hydrogen bonding in the amorphous region. After the temperature decreases to region II (112–85 °C), the secondary perfection process of EVOH occurs. The first step of region II is the generation of pair-bonded hydrogen bonds (ΔHh = −75.8 ± 3.1 kJ mol−1) of the VA repeating unit from residual free hydroxyl groups after region I, and the second step is the local rearrangement of the lattice in the imperfect crystal of the VA repeating unit. It is noted that the value of ΔHl-VA in this step is 3.2 ± 1.0 kJ mol−1, which shows that the rearrangement needs to absorb heat. The pair-bonded hydrogen bonding releases enthalpy which can be absorbed. Thus, the second step of region II in also induced by the first step. The third step of region II is the movement of the VA repeating unit with no hydrogen bonds (possibly a local rotation). The fourth step is a weak crystallization of the ET repeating unit (ΔHC-ET = −38.3 ± 0.8 kJ mol−1), which is probably caused by the movement of the VA repeating unit directly connecting with the ET repeating unit in the third step. From the view point of the enthalpy, for region I and II, the contributions of the pair-bonded hydrogen bonding to the EVOH crystallization are calculated as 42.8% and 64.6%, respectively. At the same time, the contributions of the ET repeating unit crystallization to the EVOH crystallization are 19.4% and 32.7%, respectively.
In the present study, the leading role of the hydrogen bonding on the primary crystallization and secondary perfection process of EVOH was elucidated in a quantitative way and confirmed from the molecular movements.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 51473104, 51003066), State Key Laboratory of Polymer Materials Engineering (Grant No. sklpme2014-3-06), and the Outstanding Young Scholars Foundation of Sichuan University (Grant No. 2011SCU04A13).Notes and references
- T. Cornitius, Chem. Week, 1997, 159, 32 Search PubMed.
- M. C. Gabriele, Mod. Plast., 1997, 74, 42 Search PubMed.
- K. Ito, Y. Saito, T. Yamamoto, Y. Ujihira and K. Nomura, Macromolecules, 2001, 34, 6153–6155 CrossRef CAS.
- A. Nakano, in High-Performance Membrane Dialyzers, ed. A. Saito, H. Kawanishi, A. C. Yamashita and M. Mineshima, 2011, vol. 173, pp. 164–171 Search PubMed.
- J. H. Schut, Plast. World, 1997, 55, 12 Search PubMed.
- A. Lopez-Rubio, J. M. Lagaron, E. Gimenez, D. Cava, P. Hernandez-Munoz, T. Yamamoto and R. Gavara, Macromolecules, 2003, 36, 9467–9476 CrossRef CAS.
- O. A. Scherman, R. Walker and R. H. Grubbs, Macromolecules, 2005, 38, 9009–9014 CrossRef CAS.
- J. M. Lagaron, A. K. Powell and G. Bonner, Polym. Test., 2001, 20, 569–577 CrossRef CAS.
- T.-H. Young, J.-Y. Lai, W.-M. You and L.-P. Cheng, J. Membr. Sci., 1997, 128, 55–65 CrossRef CAS.
- G. D. Guerra, N. Barbani, L. Lazzeri, L. Lelli, M. Palla and C. Rizzo, J. Biomater. Sci., Polym. Ed., 1993, 4, 643–652 CAS.
- D. Dorman, E. Otocka and F. Bovey, Macromolecules, 1972, 5, 574–577 CrossRef CAS.
- R. Foster, Modern Plastics. Mid-October Encyclopedia Issue, McGraw-Hill, New York, 1990, vol. 67, p. 73 Search PubMed.
- M. Takahashi, K. Tashiro and S. Amiya, Macromolecules, 1999, 32, 5860–5871 CrossRef CAS.
- K. Nakamae, M. Kameyama and T. Matsumoto, Polym. Eng. Sci., 1979, 19, 572–578 CAS.
- M. L. Cerrada, E. Pérez, J. M. Pereña and R. Benavente, Macromolecules, 1998, 31, 2559–2564 CrossRef CAS.
- A. Lopez-Rubio, J. M. Lagaron, E. Gimenez, D. Cava, P. Hernandez-Muñoz, T. Yamamoto and R. Gavara, Macromolecules, 2003, 36, 9467–9476 CrossRef CAS.
- T. Iwanami and Y. Hirai, Tappi J., 1983, 66, 85–90 CAS.
- Z. Peter, C. Kenyo, K. Renner, C. Krohnke and B. Pukanszky, eXPRESS Polym. Lett., 2014, 8, 756–766 CrossRef CAS.
- C. Lopez-de-Dicastillo, J. M. Alonso, R. Catala, R. Gavara and P. Hernandez-Munoz, J. Agric. Food Chem., 2010, 58, 10958–10964 CrossRef CAS PubMed.
- S. Dhawan, C. Varney, G. V. Barbosa-Canovas, J. M. Tang, F. Selim and S. S. Sablani, J. Food Eng., 2014, 128, 40–45 CrossRef CAS PubMed.
- S. Aucejo, R. Catala and R. Gavara, Food Sci. Technol. Int., 2000, 6, 159–164 CrossRef CAS PubMed.
- I. Noda, Appl. Spectrosc., 1993, 47, 1329–1336 CrossRef CAS.
- I. Noda and Y. Ozaki, in Two-Dimensional Correlation Spectroscopy – Applications in Vibrational and Optical Spectroscopy, John Wiley & Sons, Ltd, 2005 Search PubMed.
- M. Thomas and H. H. Richardson, Vib. Spectrosc., 2000, 24, 137–146 CrossRef CAS.
- S. Morita, H. Shinzawa, I. Noda and Y. Ozaki, Appl. Spectrosc., 2006, 60, 398–406 CrossRef CAS PubMed.
- T. Zhou, Y. Liu, L. Peng, Y. Zhan, F. Liu, A. Zhang and L. Li, Anal. Bioanal. Chem., 2014, 1–16 Search PubMed.
- W. Li, B. Sun and P. Wu, Carbohydr. Polym., 2009, 78, 454–461 CrossRef CAS PubMed.
- B. Zhang, H. Tang and P. Wu, Polym. Chem., 2014, 5, 5967–5977 RSC.
- H. Lai and P. Wu, Polym. Chem., 2013, 4, 3323–3332 RSC.
- W. Li and P. Wu, Polym. Chem., 2014, 5, 5578–5590 RSC.
- S. Sun and P. Wu, Macromolecules, 2012, 46, 236–246 CrossRef.
- L. Peng, T. Zhou, Y. Huang, L. Jiang and Y. Dan, J. Phys. Chem. B, 2014, 118, 9496–9506 CrossRef CAS PubMed.
- B. Sun, Y. Lin, P. Wu and H. W. Siesler, Macromolecules, 2008, 41, 1512–1520 CrossRef CAS.
- B. Tang, P. Wu and H. Siesler, J. Phys. Chem. B, 2008, 112, 2880–2887 CrossRef CAS PubMed.
- B. Zhang, H. Tang and P. Wu, Macromolecules, 2014, 47, 4728–4737 CrossRef CAS.
- L. Hou, K. Ma, Z. An and P. Wu, Macromolecules, 2014, 47, 1144–1154 CrossRef CAS.
- Y. Jing, H. Tang and P. Wu, Polym. Chem., 2013, 4, 5768–5775 RSC.
- Y. Jin, W. Wang and Z. Su, Polym. Chem., 2012, 3, 2430–2435 RSC.
- T. Zhou, L. Peng, Y. Liu, Y. Zhan, F. Liu and A. Zhang, Vib. Spectrosc., 2014, 70, 137–161 CrossRef CAS PubMed.
- J. Luo, T. Zhou, X. Fu, H. Liang and A. Zhang, Eur. Polym. J., 2011, 47, 230–237 CrossRef CAS PubMed.
- Z. Chen, T. Zhou, J. Hui, L. Li, Y. Li, A. Zhang and T. Yuan, Vib. Spectrosc., 2012, 62, 299–309 CrossRef CAS PubMed.
- T. Zhou, Z. Wu, Y. Li, J. Luo, Z. Chen, J. Xia, H. Liang and A. Zhang, Polymer, 2010, 51, 4249–4258 CrossRef CAS PubMed.
- T. Zhou, A. Zhang, C. S. Zhao, H. W. Liang, Z. Y. Wu and J. K. Xia, Macromolecules, 2007, 40, 9009–9017 CrossRef CAS.
- L. P. Kuhn, J. Am. Chem. Soc., 1952, 74, 2492–2499 CrossRef CAS.
- S. Krimm, Adv. Polym. Sci., 1960, 2, 51–172 CrossRef CAS.
- J. M. Lagaron, E. Gimenez, R. Catala and R. Gavara, Macromol. Chem. Phys., 2003, 204, 704–713 CrossRef CAS PubMed.
- H. S. Mansur, C. M. Sadahira, A. N. Souza and A. A. P. Mansur, Mater. Sci. Eng., C, 2008, 28, 539–548 CrossRef CAS PubMed.
- K. Sugiura, M. Hashimoto, S. Matsuzawa and K. Yamaura, J. Appl. Polym. Sci., 2001, 82, 1291–1298 CrossRef CAS PubMed.
- L. Dai and L. Ying, Macromol. Mater. Eng., 2002, 287, 509–514 CrossRef CAS.
- N. A. Peppas, Makromol. Chem., 1977, 178, 595–601 CrossRef CAS PubMed.
- J. M. Gohil, A. Bhattacharya and P. Ray, J. Polym. Res., 2006, 13, 161–169 CrossRef CAS.
- D. Swinehart, J. Chem. Educ., 1962, 39, 333 CrossRef CAS.
- P. Yang, X. Wang, H. Fan and Y. Gu, Phys. Chem. Chem. Phys., 2013, 15, 15333–15338 RSC.
- G. A. Senich and W. J. MacKnight, Macromolecules, 1980, 13, 106–110 CrossRef CAS.
- L. S. Teo, C. Y. Chen and J. F. Kuo, Macromolecules, 1997, 30, 1793–1799 CrossRef CAS.
- Q. Yuan, T. Zhou, L. Li, J. Zhang, X. Liu, X. Ke and A. Zhang, RSC Adv., 2015, 5, 31153–31165 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra13486b |
| This journal is © The Royal Society of Chemistry 2015 |







