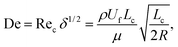Improved understanding of particle migration modes in spiral inertial microfluidic devices
Nan Xiang,
Zhiguo Shi,
Wenlai Tang,
Di Huang,
Xinjie Zhang and
Zhonghua Ni*
School of Mechanical Engineering, Jiangsu Key Laboratory for Design and Manufacture of Micro-Nano Biomedical Instruments, Southeast University, Nanjing, 211189, China. E-mail: nzh2003@seu.edu.cn
First published on 1st September 2015
Abstract
We investigated the migration dynamics of particles with multi-scale sizes in a classical spiral inertial microfluidic device. Our experimental results demonstrate that in curved low-aspect-ratio channels particles of different confinement ratios behave in three migration modes, including focusing, rough focusing, and non-focusing. The migration behaviors of specific-sized particles can be switched flexibly between these three modes by redesigning the characteristic length of the channel cross-section. The mechanics underlying these migration modes were then interpreted in terms of the competition between Brownian motion, inertial lift effects and secondary flow effects. The detailed particle migration dynamics in each migration mode were characterized over a wide range of flow rates to further the understanding of multi-mode migration mechanisms in Dean-coupled inertial flows. Finally, the effectiveness of the discovered three-mode-migration theory was validated in an experiment of bioparticles with polydisperse sizes. The obtained results in our work would provide valuable insights into the flexible control of particle migration and the separation of multi-scale particles in curved channel systems.
Introduction
High-throughput label-free manipulations of micro/nano-materials, such as sheathless focusing, size/shape-dependent sorting and controllable trapping, have been regarded as an important pretreatment step for biochemical microanalysis and on-chip diagnosis.1,2 As one of the newly emerging passive approaches, inertial microfluidics with curved channels, which employs the traditionally neglected fluid inertia effects in finite-Reynolds-number channel flows, is poised to become a potential technique for the dynamic control of particle/cell motions.3,4 Compared with most of current manipulation schemes, this technique offers significant advantages, such as simple structure, high processing throughput and easy operation. In addition, the utilization of spirals as the curved channel topology effectively reduces the overall footprint of the device and further permits its flexible integration with existing Lab-on-a-chip (LOC) units. Therefore, spiral inertial microfluidic devices have attracted increasing interests in recent years, and have been successfully employed in various biomedical applications, such as sheathless microflow cytometry,5 vortex-assisted DNA delivery,6 size-dependent cell separation,7–10 and high-yield cell-in-droplet encapsulation.11In addition to novel applications, much attention has been devoted to elucidating the underlying physics of fluid flow or particle migration in these spiral inertial microfluidic devices. Specifically, researchers have investigated the effects of channel topology (gradually widening or double spiral),12–14 curvature radius,15 cross-sectional shape (rectangular or trapezoidal)16 and aspect ratio17 on particle migration behaviors, thus realizing the optimization of these critical structural parameters for device miniaturization or operation protocol improvement. We have also made some efforts in this line of research, including investigations into the flow-rate regulation mechanisms,18 particle finite-size effects,19,20 and formation mechanisms of secondary flow.21
However, nearly all the above-mentioned biomedical applications or fundamental investigations have exclusively concerned the “focused particles” (typical diameters of 5–20 μm) that can be focused into regular arrays at specific flow conditions due to the potential applicability of particle/cell focusing to microflow cytometers or continuous-flow sorters. Little attention has been paid to smaller and unfocused particles, that is, the migration mechanisms of these smaller particles are still unclear. Understanding the migration behaviors or modes of particles with sizes ranging from micro- to submicro/nano-scales would help realize flexible control of particle motions, and achieve high-throughput separation of real biochemical samples (e.g., body fluids) which may compose of particles with multi-scale sizes.
Herein, we investigated the migration dynamics of particles with multi-scale sizes in classic spiral inertial microfluidic devices. The experimental results show that particles with different confinement ratios behave in three migration modes in curved low-aspect-ratio channels. On this basis, we analyzed the mechanics underlying these particle migration modes, and then performed a quantitative investigation on the detailed particle migration behaviors in each mode. Finally, the effectiveness of the proposed three mode migration was successfully validated in the dynamics of polydisperse bioparticles. The experimental findings obtained in this work would improve the understanding of inertia-induced particle migration and provide insights into the dynamic and flexible control of complex particles in curved channel systems.
Methods and theory
Experimental methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
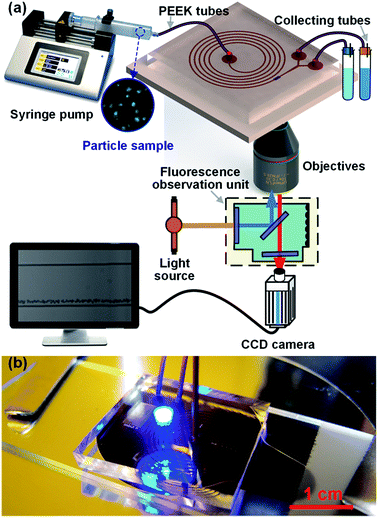
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, and the channel height h was fixed at 50 μm). The spacing between two adjacent channel loops was set at 500 μm to ensure sufficient areas for robust bonding, and the initial radius of the spiral was set at 3.5 mm for positioning the large inlet system. A special gradual expansion channel with a Y-shaped outlet system was adopted to make the device able to be expanded for automatic particle/cell enrichment. This device was rapidly prototyped in polydimethylsiloxane (PDMS) using the maskless lithography technique and micromolding method. Briefly, a layer of 50 μm thick SU-8 photoresist (Microchem) was spun coat onto a cleaned 4′′ silicon wafer, and then patterned with 365 nm UV light via a maskless lithography machine (SF-100, Intelligent Micro Patterning). After finishing the developing and hard baking steps, the obtained SU-8 master mold was casted with degassed PDMS liquid (Sylgard 184, Dow Corning), and then moved to a 80 °C oven (Thermal Scientific) for PDMS curing. After curing, orifices were punched at the inlet and outlets using a Harris Uni-Core biopsy micropunch (0.75 mm), and then an irreversible PDMS-to-glass bonding procedure was carried out with the assistance of UV/Ozone treatment (144AX-220, Jelight Company, Inc.). The finished spiral inertial microfluidic device is demonstrated in Fig. 1(b). Although the total channel length reaches ∼16 cm, the overall footprint of our device is only ∼2 cm2, which permits this miniaturized device flexibly be integrated as a high-throughput pretreatment module with other existing LOC units.
3, and the channel height h was fixed at 50 μm). The spacing between two adjacent channel loops was set at 500 μm to ensure sufficient areas for robust bonding, and the initial radius of the spiral was set at 3.5 mm for positioning the large inlet system. A special gradual expansion channel with a Y-shaped outlet system was adopted to make the device able to be expanded for automatic particle/cell enrichment. This device was rapidly prototyped in polydimethylsiloxane (PDMS) using the maskless lithography technique and micromolding method. Briefly, a layer of 50 μm thick SU-8 photoresist (Microchem) was spun coat onto a cleaned 4′′ silicon wafer, and then patterned with 365 nm UV light via a maskless lithography machine (SF-100, Intelligent Micro Patterning). After finishing the developing and hard baking steps, the obtained SU-8 master mold was casted with degassed PDMS liquid (Sylgard 184, Dow Corning), and then moved to a 80 °C oven (Thermal Scientific) for PDMS curing. After curing, orifices were punched at the inlet and outlets using a Harris Uni-Core biopsy micropunch (0.75 mm), and then an irreversible PDMS-to-glass bonding procedure was carried out with the assistance of UV/Ozone treatment (144AX-220, Jelight Company, Inc.). The finished spiral inertial microfluidic device is demonstrated in Fig. 1(b). Although the total channel length reaches ∼16 cm, the overall footprint of our device is only ∼2 cm2, which permits this miniaturized device flexibly be integrated as a high-throughput pretreatment module with other existing LOC units.
Theoretical background
The fluid flowing through a curved channel induces a specific hydrodynamic effect, the secondary flow (also named as Dean flow),22–24 which is regarded as a relatively minor flow superimposed on the main flow. This secondary flow can be illustrated as two symmetric counter-rotating vortices (i.e., Dean vortices) located in the upper and lower half of the channel cross-section. The magnitude of this rotational flow can be described using a dimensionless number named Dean number (De) as follows:25–27where Rec is the famous channel Reynolds number which describes a measure of the relative importance of inertial effects and viscous effects, δ is the curvature ratio which is defined as δ = Lc/2R, ρ is the fluid density, Uf is the mean velocity of flowing fluids, Lc is the characteristic length of the channel cross-section, μ is the dynamic viscosity of flowing fluids, and R is the channel radius.
The lateral Dean drag (FD) induced by this cross-sectional secondary flow forces the flowing particles to migrate in a direction perpendicular to the main flow. The magnitude and direction of this force are determined by the local secondary flow field near the particle. A scaling of the Dean drag force can be derived as follows by assuming the Stokes drag:28
| FD ∝ ρUm2apLc2R−1, |
Moreover, in finite-Reynolds-number channel flows, the parabolic nature of the main velocity profile results in a shear-induced lift force (FLS) directing down the shear gradient toward the channel wall, while the particle–wall interaction induces a wall-induced lift force (FLW) which pushes the particle away from the channel wall.29 The relation describing the net magnitude of these two forces (inertial lift force, FL) is provided as follows:30–32
In addition to the above-mentioned two main lateral forces (FD and FL), flowing particles may also experience other forces, such as mainstream viscous drag force, buoyancy force, and centrifugal force. However, these forces are negligible in the analysis of the force balance because the mainstream viscous drag force along the main flow direction contributes nothing to the lateral migration of the particles and the magnitudes of the buoyancy force and centrifugal force are extremely low compared with that of the inertial lift force and Dean drag force.15,16,33 Therefore, particles were assumed to be acted on exclusively by the superposition of the inertial lift force and Dean drag force. Then, a useful force ratio (Rf = FL/FD) can be defined to estimate the competition between these two forces. The characteristic length (Lc) of the low-aspect-ratio channel cross-section, as suggested in previous studies,34,35 can be replaced by the channel height (h), and thus a scaling for this force ratio can be derived as follows:
As can be seen from the above scaling, the particle behavior is found to be determined by the curvature ratio δ, the dimensionless lift coefficient fL(Rec, Xp) which is indirectly affected by flow rate and initial particle position, and the particle confinement ratio (CR = ap/h). The regulation mechanisms of structural (e.g., channel width, curvature ratio, and cross-sectional shape) or operational (e.g., flow rate) parameters on particle dynamics have been reported in previous studies.15–18 However, the effects of particle confinement ratio on migration dynamics have not been systematically investigated. Previous studies only suggested an empirical guideline that particles satisfying ap/h ≥ 0.07 can be well-focused under certain operating conditions.7,35
Three migration modes and particle dynamics
Particle suspensions with different sizes (CRs = 0.004–0.2) were separately pumped into the fabricated spiral inertial microfluidic device. For each size of particles, various driving flow rates (Q = 100–700 μl min−1, the corresponding Dean numbers at the inlet were De = 1.73–12.08) were used. The stacked fluorescent stream images which clearly demonstrate the possible particle distribution across the channel width over a certain time period are selectively grouped in Fig. 2. As mentioned in the last section, both the driving flow rate and particle confinement ratio (CR) would significantly affect the lateral migration of flowing particles in Dean-coupled inertial flows. This is now well confirmed in our experimental observations. Nevertheless, the detailed regulation mechanisms of these two parameters are completely different. The flow-rate effects on particle migration are mainly embodied in the changes of the particle stream width and position,18 while the particle confinement ratio directly determines the migration modes of flowing particles. Through a careful analysis of our experimental results (CRs = 0.004–0.2) and a synthesis of past research on the migration behaviors of particles with CRs of 0.07–0.3,7–9,11–18 we concluded that particles flowing in a curved low-aspect-ratio channel behave in three different migration modes. Specifically, when the CR is larger than the critical cutoff value (CRc = 0.07), particles can migrate and assemble into a well-ordered stream located close to the inner wall under specific flow rates and at specific channel lengths. These particles are regarded as being in the focusing mode (Mode 1 in Fig. 2) which has attracted the most research interests due to the potential application of particle focusing as an important pretreatment step in size-dependent particle/cell sorter7–10 or sheathless microflow cytometer.5 As the CR decreases to be smaller than the cutoff value, particles can migrate to form a relatively broad particle band due to the generation of a particle-free region near both inner and outer channel walls. These particles are treated as being in the rough focusing mode (Mode 2 in Fig. 2). When the CR further decreases to a certain extent (<∼0.01), flowing particles are dispersed all over the channel regardless of flow rate. These particles are regarded as being in the non-focusing mode (Mode 3 in Fig. 2). The migration behaviors of specific-sized particles can be switched flexibly between these three modes when the characteristic length of the channel cross-section is redesigned. In the following part, we will present a more quantitative analysis on the dynamics of selected-sized particles under each migration mode.Multi-particle dynamics under the focusing mode
The particle dynamics under the focusing mode have been most extensively investigated due to the potential application of particle focusing as an important sample pretreatment step.5–13,16,26,27,31,36 However, the understandings of particle focusing dynamics were still limited to the single or binary particle system, with no attention being paid to the multi-particle system. In this work, we investigated and compared the focusing dynamics of particles with three different CRs (CR = 0.096, 0.1464 and 0.1980). As demonstrated in previous studies,2,4,28,29 the particles under the focusing mode can migrate towards and occupy the equilibrium positions at specific flow rates under the complex coupling of the inertial lift force and the Dean drag force. This particle focusing phenomenon is now well reduplicated in our experimental results (see Mode 1 in Fig. 2). To probe into the multi-particle focusing dynamics, we defined a dimensionless parameter, named as normalized stream width, through dividing the measured particle stream width by particle diameter, and then plotted the calculated stream widths together with the measured focusing positions as a function of De in Fig. 3. From Fig. 3(a), we found that the particle with a larger CR commonly owns a better focusing quality (i.e., smaller normalized stream width), which agrees well with the theoretical analysis that the net lateral force |FL − FD| acting on the flowing particles is positively correlated to the CR. However, a sudden changing of particle stream widths at middle flow rates is observed in the focusing spectrum of particles with a CR of 0.1980 due to the generation of double-position (DP) focusing (see the inset (ii) of Fig. 3(a)). The reason for this instable DP focusing can be explained as the stepwise particle transferring from the original equilibrium position to another more stable one.18 After all particles have been transferred to the new stable equilibrium position, the DP focusing reverts to the normal single stream focusing. Besides the DP focusing, another difference observed in the width variation curves of these three particles is that the stream widths of particles with CRs of 0.096 and 0.1464 first rapidly narrow down to form a tightly focused stream, and then gradually defocus with the increase of De while the stream width of particles with a CR of 0.1980 continuously decreases with the increase of De and achieves a better focusing quality at higher Des.To deepen the understanding of multi-particle focusing dynamics, we also measured the lateral focusing positions of these three particles, and plotted these values as a function of De, as illustrated in Fig. 3(b). From this figure, we noticed that the focusing positions of particles with CRs of 0.096 and 0.1464 move towards the inner wall at first, and then shifts towards the outer wall at larger Des. As a sharp comparison, the particle with a CR of 0.1980 continuously shifts towards the inner wall with increasing De. Through a combined analysis of the width and position variation curves, we deduced that the differences between the focusing dynamics of these three tested particles are caused by the difference in dominant force regimes. For small particles (CR = 0.096 and 0.1464), the dominant force acting on particles will turn from the inertial lift force directed towards the inner wall to Dean drag force directed towards channel centerline due to the fact that the Dean drag force increases much faster, and will finally surpass the originally dominated inertial lift force with increasing flow rates. The dominant Dean drag force at high flow rates enables the particles to move towards the channel centerline, and broadens the particle focusing stream as a result of enhanced Dean mixing effects. We then plotted the detailed force regime distributions of these three particles in the inset (i) of Fig. 3(a). As can be seen from this regime map, the transition flow rate at which the dominant force shifts from inertial lift force to Dean drag force gradually increases with increasing CR. For particles with a CR of 0.1980, the Dean drag dominated regime was not observed in our experiments, which well explains the absence of the outward-shifting of particle focusing stream under the tested flow rate range. To further obtain the transition flow rate (Qt) of this sized particle, a rigid channel device which can bear a much higher pressure is needed. Although the particles with a CR of 0.1980 are always tied to the inertial regime, the force balance acting on these large particles is much more sensitive to the flow rate, as compared with that acting on other two small particles due to the fact that the force ratio Rf is in direct proportion to CR3fL(Rec, Xp) (where the lift coefficient fL is a function of flow rate). Therefore, the equilibrium positions of large particles are easily influenced by the flow rate, which provides a possible interpretation for the generation of DP focusing in the dynamics of particles with a CR of 0.1980.
Another novel finding worth mentioning is that in addition to particle size, the relative focusing position of these particles is found to be dependent also on flow rate. From the position variation curves illustrated in Fig. 3(b), we found that the whole tested flow rate range can be divided into four different regimes. Specifically, at the beginning flow rates (Stage I), the focusing position of small particles is closer to the inner wall as compared with that of large particles, occurred as “Small-Middle-Large (S-M-L)”. With increasing flow rate to be larger than the Qt-s (Qt-s denotes the transition flow rate of small particles), the small particles would move towards the outer wall under the dominant Dean drag force (in the Dean regime), and finally interchange their lateral positions with that of middle-sized particles. Therefore, the relative focusing position of these three particles would appear as M-S-L (Stage II), as illustrated in the inset (iii) of Fig. 3(b). Then, the small particles would keep outward shifting, making the relative focusing position turn to be M-L-S (Stage III). After the flow rate has further been increased to surpass the Qt-m, the middle particles also begin to be dominated by the Dean drag force, and turn to shift towards the channel centerline. Therefore, the middle particles would pass across the focusing position of large particles, generating a well-known L-M-S distribution (Stage IV) that the large particles focus closer to the inner wall,7,14,26,35 as illustrated in the inset (iv) of Fig. 3(b). For Stages I and II, the focusing qualities or the distances between adjacent particle focusing streams are not acceptable. To achieve high-throughput separation of these three particles, it is better to choose a flow rate in the later Stages III and IV.
Particle migration behaviors under the rough focusing mode
The migration behaviors of particles with CRs smaller than the critical cutoff value (CRc = 0.07) were commonly neglected in previous studies due to its limited application potentials. For these particles, the Dean drag force acting on particles would surpass the inertial lift force in magnitude,28 and dominates the lateral migration of flowing particles due to the fact that the dimensionless force ratio (Rf) is proportional to CR2. It was also found in previous studies7,18 that the Dean drag force increases much faster than the inertial lift force as the flow rate increases, which means that the Dean drag force would play an increasingly dominant role in the lateral migration of particles at higher flow rates under this migration mode. In this case, instead of being focused at specific lateral positions, the flowing particles would get entrained and circulated in one of the two Dean vortices located in the upper and lower half of the channel respectively. Herein, we selected particles with a CR of 0.042 to investigate and analyze the detailed particle migration dynamics under this mode. From the fluorescent stream images grouped in Fig. 2 (Mode 2), we found that at the starting flow rate of De = 1.73, particles initially located near the inner wall (see particle 1 in the inset (i) of Fig. 4(a)) are spiraled into the effective region of the vortex under the Dean drag force directed outward, generating a particle-free region near the inner wall. The effective region of the vortex is defined as the region where the local flow field is strong enough to drag particles into the circulation, and the local field for dragging particles can be strengthened via increasing the main flow rate.21 Since at low flow rates, the Dean drag force directed inward (near the top and bottom channel walls) is much weaker than that directed outward (near the middle channel plane),33 particles located near the outer wall (see particle 2 in the inset (i) of Fig. 4(a)) can only reflow into the circulation at much higher flow rates, finally resulting in the generation of a new particle-free region near the outer wall.In attempts to elucidate the effects of flow rate on particle migration behaviors under this mode, we quantitatively measured the particle stream widths and intensity profiles across the channel width under different flow rates. The obtained particle stream widths were plotted as a function of De in Fig. 4(a). As can be seen from this figure, the particle stream width decreases rapidly at the starting flow rates due to, as demonstrated above, the generation of the double particle-free regions near channel walls; but then it begins to increase gradually with increasing De. A further analysis of the intensity distributions at this flow rate range shows that the outer boundary of the particle stream first moves toward and then shifts away from the inner wall while the inner boundary remains almost unchanged during the whole flow rate range (see Fig. 4(b)). It is also found that these intensity profiles are asymmetrically biased toward the inner channel wall, indicating that more particles aggregate in the inner channel region. These two findings indirectly reflect some formation and development mechanisms of the cross-sectional Dean flow. In curved channels, the maximum velocity point of the plane Poiseuille flow and the center of Dean vortices are proved to shift from the channel center toward the inner channel wall,22,36 which can well explain the observed asymmetrical distribution of particles. In addition, the local velocities of Dean vortices near the outer channel wall, which are initially much weaker than that near the inner channel wall, would gradually strengthen with increasing the main flow rate21,33 so that the effective region of the vortex for dragging the particle into the circulation gradually widens. Therefore, the particle stream width gradually increases with the increase of the main flow rate in the later stage. The conclusion that the particle migration behavior under the rough focusing mode is determined by the features of the cross-sectional vortices (e.g., the local velocity field or shape and position of vortices) provides a useful guideline for designing curved microfluidic systems that the particle dynamics in this mode can be flexibly controlled by regulating the dimension or shape of the channel cross-section.
Particle distributions under the non-focusing mode
As the CR decreases to a certain extent, both the inertial lift force and the Dean drag force become very weak while the Brownian diffusion of particles is significantly enhanced and would dominate the particle migration. In this work, we investigated the migration behaviors of nanoparticles with an extremely low CR of 0.004 in Dean-coupled inertial flows. The generation of single/double particle-free region(s) observed in the rough focusing mode was not found in this mode where particles are always scattered across the channel within the tested flow rate range (see Mode 3 in Fig. 2). By analyzing the fluorescence intensity profiles illustrated in Fig. 5(a), we found that the intensity distribution across the channel width shows a parabolic profile, indicating that these small particles would, to some extent, aggregate near the channel center. The non-uniform particle distribution across the channel width would be significantly enhanced with increasing flow rate. This interesting nanoparticle “focusing” phenomenon may be attributed to the shear-induced migration effect that drives particles to migrate from the high-shear-rate region near the channel wall to the low-shear-rate region near the channel center.37 The finding of this nano-focusing phenomenon blazes a new path for future high-throughput concentration or enrichment of nano-materials. Similar aggregation phenomena has also been found in the migration behaviors of some biological macromolecules (e.g., DNA molecules) in viscoelastic flows.38 However, facing with the problems of small channel dimension employed and high viscosity of the viscoelastic suspension fluids, the processing throughput was limited to be only ∼15 μl h−1, which is far more than enough for real-word applications where the biological samples to be processed is commonly in ml-scale. As a comparison, our spiral inertial microfluidic device offers a throughput up to ∼ml min−1 level without the assistance of energy-consuming external fields or demanding channel structures. To further quantitatively evaluate this nanoparticle aggregation effect, we defined a dimensionless parameter, aggregation degree (AD = ICenter/IWall), through dividing the average fluorescence intensity (ICenter) near the channel centerline by the average fluorescence intensity (IWall) near channel walls. The obtained aggregation degrees under different flow rates are then plotted as a function of De in Fig. 5(b). From this figure, it is confirmed that the aggregation degree increases with the increase of flow rate. The aggregation velocity at low flow rates is found to be much faster than that at high flow rates, which indicates that the aggregation degree would trend to be constant after the flow rate increase to be high enough. An exponential function AD = 1.899–0.763*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.099De) (R2 = 0.97) can be well employed to describe the variation of aggregation degree according to De.
exp(−0.099De) (R2 = 0.97) can be well employed to describe the variation of aggregation degree according to De.
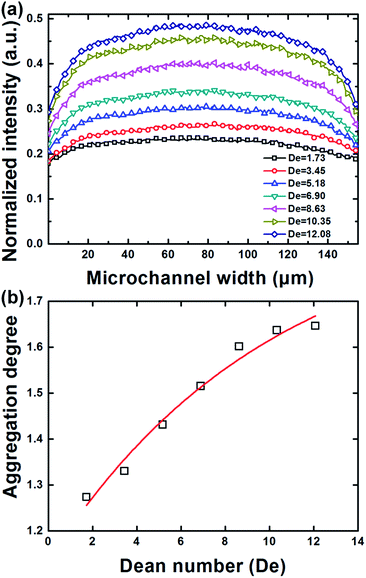 | ||
| Fig. 5 (a) Fluorescence intensity distributions across the channel width at various flow rates (De = 1.73–12.08) under the non-focusing mode. (b) The measured aggregation degree as a function of De. | ||
Besides the nano-particle aggregation phenomenon near the channel center, we also found in Fig. 5(a) that the overall intensity across the channel width gradually increases with increasing flow rate, indicating that particles may also aggregate in the middle plane parallel to the channel bottom due to the shear gradient along the channel height. The Poiseuille flow in channels with a rectangular cross-section would yield a much higher shear gradient along the shortest side of the cross-section (i.e., the channel height in this work),35 which means particles would aggregate more easily in the middle region along the channel height. In addition, previously reported numerical studies revealed that the shear gradient along both directions (channel width and height) would increase significantly with the increase of the driving flow rate,21 which leads to the prominence of this aggregation phenomenon at higher flow rates. However, the detailed physics underlying this finding of nanoparticle focusing in Dean-coupled inertial flows or the migration behaviors of other irregular nanomaterials (e.g., nanowire and nanotube) are still not well understood, and thus more solid theoretical or experimental investigations are needed in future studies.
Validation of migration modes in the dynamics of complex bioparticles
On the basis of the improved understanding of particle dynamics under each migration mode, we carried out an investigation to validate the effectiveness of the discovered three mode migration in the dynamics of complex bioparticle systems. In this experiment, the zymosan bioparticles (also called “ghost cells”), which contain submicron scale debris, were selected as the manipulation model. The size of this bioparticle is strongly polydisperse with its average diameter size (3–4 μm) happens to satisfy the critical cutoff CR (CRc = 0.07) for achieving high-quality particle focusing in our channel design. In addition, as compared with the above-used polymer particles with ideal spherical shapes and monodisperse sizes, the zymosan bioparticle offers much more complex features, such as broader size distribution or greater deformability. Therefore, the focusing dynamics of this bioparticle would be more interesting and may provide helpful insights for flexibly processing complex biological specimens.To better observe the contained small components or debris, the zymosan bioparticles were covalently labeled with fluorophores, and then diluted in sterile phosphate-buffered saline (Sigma) containing 0.5 wt% Tween 20 to form homogeneous particle suspensions with extremely low concentrations. These particle suspensions were then introduced into the spiral channel device at the same flow rates used above (Q = 100–700 μl min−1). The particle migration dynamics near the outlets were captured and overlaid to obtain the composite fluorescent stream images, as grouped in Fig. 6(a). From this focusing spectrum, it is found that the focusing quality of this bioparticle is noticeably less desirable than that of particles under the focusing mode, but much better than that of particles under the rough focusing mode. This difference lies in the polydisperse size distribution which makes particles with CRs ≥ 0.07 being under the focusing mode, and particles with 0.01 < CRs < 0.07 being under the rough focusing mode. In addition, the deformation induced by the high shear rate would change the shapes or characteristic dimensions of particles, which also makes the focusing quality worse.
To probe into the detailed migration dynamics of this complex bioparticle, we determined the boundaries of the particle stream by marking the points where the intensity crosses 20% of the peak value, and depicted the possible particle distributions at different flow rates in Fig. 6(b). From this figure, we found that both the inner and outer boundaries of the particle stream first move towards the inner wall, and then shift towards the outer wall with increasing flow rates. The shifting velocity of the outer boundary is found to be much higher than that of the inner boundary, indicating that particles close to the channel centerline experience much stronger net forces. We then defined a dimensionless width through dividing the calculated distance between the two boundaries by the average particle diameter to evaluate the effects of flow rate on particle stream width (see the Fig. 6(c)). From this columnar distribution, it is observed that the narrowest stream width occurs at the middle flow rates of De = 3.45 and 5.18 rather than at the highest flow rate, which agrees well with the dynamics of above-investigated particles under the focusing mode. However, due to the existence of small unfocused particles, the defocusing effect under high flow rates is more obviously as compared with that of particles under the focusing mode. In addition, we measured the average fluorescence intensities near the outer channel wall, and plotted these values as a function of De in Fig. 6(d). It is interesting to find that except the intensity under the De of 3.45, the measured intensities gradually increase with the increase of De, which indicates that the contained small submicron or nanoscale debris are under the non-focusing mode, and the interesting nano-focusing phenomenon is also observed in the migration dynamics of this bioparticle. The high intensity observed at the starting flow rate of De = 3.45 is caused by the present of rough focusing particles which would get entrained in the Dean vortex, and generate a particle-free region near the inner wall. In conclusion, all the three discovered migration modes are well validated in the focusing experiments of this polydisperse sized bioparticle, and the migration dynamics of this bioparticle are found to be a complex of behaviors under each migration mode.
Conclusions
In this work, we characterized the migration dynamics of particles with different CRs in a spiral inertial microfluidic device. Experimental results showed that particles behave in three different migration modes in curved low-aspect-ratio channels according to their CRs. More importantly, it was found that the particle migration behaviors can dynamically be switched between these three modes when the channel dimension is regulated, providing a useful guideline for flexibly controlling particle motions. For the purpose of furthering the understanding of these migration modes, we investigated the detailed migration dynamics of selected-sized particles in each mode, and analyzed the mechanics underlying these different migration modes.For particles in the non-focusing mode, the particle dynamics are dominated by the Brownian motion since the effects of fluid inertia on lateral particle migration are very weak. Thus, the particles are dispersed throughout the channel within the whole tested flow rate range. Nevertheless, an interesting parabolic distribution of particle concentration across the channel width was observed, which indicates that particles would aggregate near the channel center with the increase of the flow rate. For particles in the rough focusing mode, the Dean drag force acting on particles surpasses the inertial lift force in magnitude and thus dominates the lateral migration of the particles. Owing to the dragging effects of Dean vortices, a particle-free region is generated near both inner and outer channel walls, which leads to the formation of a wide particle band across the channel width. The width and location of this particle band were found to be determined by the features of the cross-sectional vortices. This means that we can flexibly control the particle motions by regulating the dimension or shape of the channel cross-section. For particles in the focusing mode, particles migrate to form a tightly-focused particle stream under the coupling of Dean drag force and inertial lift force. The multi-particle dynamics under the focusing mode were analyzed, and an interesting four-stage development of particle focusing positions across the channel width was found. Finally, the effectiveness of the discovered three mode migration was successfully validated in the dynamics of polydisperse-sized bioparticles. The experimental findings of the particle migration modes and behaviors would provide insights into the dynamic and flexible control of particles in curved channel systems.
Acknowledgements
This research work was supported by the National Natural Science Foundation of China (51505082, 51505083, 51375089), the National Basic Research Program of China (2011CB707601), and the Natural Science Foundation of Jiangsu Province (BK20150606).Notes and references
- X. Mu, W. Zheng, J. Sun, W. Zhang and X. Jiang, Small, 2013, 9, 9–21 CrossRef CAS PubMed
.
- X. Xuan, J. Zhu and C. Church, Microfluid. Nanofluid., 2010, 9, 1–16 CrossRef
.
- A. Karimi, S. Yazdi and A. M. Ardekani, Biomicrofluidics, 2013, 7, 021501 CrossRef CAS PubMed
.
- H. Amini, W. Lee and D. Di Carlo, Lab Chip, 2014, 14, 2739–2761 RSC
.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli, N. Kaval, C. J. Seliskar and I. Papautsky, Biomed. Microdevices, 2010, 12, 187–195 CrossRef PubMed
.
- J. Wang, Y. Zhan, V. M. Ugaz and C. Lu, Lab Chip, 2010, 10, 2057–2061 RSC
.
- S. S. Kuntaegowdanahalli, A. A. S. Bhagat, G. Kumar and I. Papautsky, Lab Chip, 2009, 9, 2973–2980 RSC
.
- J. Sun, M. Li, C. Liu, Y. Zhang, D. Liu, W. Liu, G. Hu and X. Jiang, Lab Chip, 2012, 12, 3952–3960 RSC
.
- L. Wu, G. Guan, H. W. Hou, A. A. S. Bhagat and J. Han, Anal. Chem., 2012, 84, 9324–9331 CrossRef CAS PubMed
.
- M. E. Warkiani, G. Guan, K. B. Luan, W. C. Lee, A. A. S. Bhagat, P. Kant Chaudhuri, D. S.-W. Tan, W. T. Lim, S. C. Lee, P. C. Y. Chen, C. T. Lim and J. Han, Lab Chip, 2014, 14, 128–137 RSC
.
- E. W. M. Kemna, R. M. Schoeman, F. Wolbers, I. Vermes, D. A. Weitz and A. van den Berg, Lab Chip, 2012, 12, 2881–2887 RSC
.
- J. Sun, C. Liu, M. Li, J. Wang, Y. Xianyu, G. Hu and X. Jiang, Biomicrofluidics, 2013, 7, 011802 CrossRef PubMed
.
- J. Seo, M. H. Lean and A. Kole, J. Chromatogr., A, 2007, 1162, 126–131 CrossRef CAS PubMed
.
- A. Russom, A. K. Gupta, S. Nagrath, D. Di Carlo, J. F. Edd and M. Toner, New J. Phys., 2009, 11, 75025 CrossRef PubMed
.
- J. M. Martel and M. Toner, Sci. Rep., 2013, 3, 3340 Search PubMed
.
- G. Guan, L. Wu, A. A. Bhagat, Z. Li, P. C. Y. Chen, S. Chao, C. J. Ong and J. Han, Sci. Rep., 2013, 3, 1475 Search PubMed
.
- J. M. Martel and M. Toner, Phys. Fluids, 2012, 24, 032001 CrossRef PubMed
.
- N. Xiang, H. Yi, K. Chen, D. Sun, D. Jiang, Q. Dai and Z. Ni, Biomicrofluidics, 2013, 7, 044116 CrossRef PubMed
.
- D. Sun, Y. Wang, D. Jiang, N. Xiang, K. Chen and Z. Ni, Appl. Phys. Lett., 2013, 103, 071905 CrossRef PubMed
.
- D. Sun, N. Xiang, K. Chen and Z. Ni, Acta Phys. Sin., 2013, 62, 24703 Search PubMed
.
- D. Sun, N. Xiang, D. Jiang, K. Chen, H. Yi and Z. Ni, Chin. Phys. B, 2013, 22, 114704 CrossRef
.
- W. R. Dean, Philos. Mag., 1928, 5, 673–695 CrossRef PubMed
.
- T. Scherr, C. Quitadamo, P. Tesvich, D. S.-W. Park, T. Tiersch, D. Hayes, J.-W. Choi, K. Nandakumar and W. T. Monroe, J. Micromech. Microeng., 2012, 22, 055019 CrossRef PubMed
.
- J. Zhang, W. Li, M. Li, G. Alici and N.-T. Nguyen, Microfluid. Nanofluid., 2013, 17, 305–316 CrossRef
.
- S. A. Berger, L. Talbot and L. S. Yao, Annu. Rev. Fluid Mech., 1983, 15, 461–512 CrossRef
.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Lab Chip, 2008, 8, 1906–1914 RSC
.
- J. Zhang, S. Yan, R. Sluyter, W. Li, G. Alici and N.-T. Nguyen, Sci. Rep., 2014, 4, 4527 Search PubMed
.
- D. Di Carlo, D. Irimia, R. G. Tompkins and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18892–18897 CrossRef CAS PubMed
.
- D. Di Carlo, Lab Chip, 2009, 9, 3038–3046 RSC
.
- E. S. Asmolov, J. Fluid Mech., 1999, 381, 63–87 CrossRef CAS
.
- C. Liu, G. Hu, X. Jiang and J. Sun, Lab Chip, 2015, 15, 1168–1177 RSC
.
- J. Zhang, S. Yan, G. Alici, N.-T. Nguyen, D. Di Carlo and W. Li, RSC Adv., 2014, 4, 62076–62085 RSC
.
- D. R. Gossett and D. Di Carlo, Anal. Chem., 2009, 81, 8459–8465 CrossRef CAS PubMed
.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Phys. Fluids, 2008, 20, 101702 CrossRef PubMed
.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Microfluid. Nanofluid., 2009, 7, 217–226 CrossRef CAS
.
- N. Nivedita and I. Papautsky, Biomicrofluidics, 2013, 7, 054101 CrossRef PubMed
.
- D. Leighton and A. Acrivos, J. Fluid Mech., 1987, 181, 415–439 CrossRef CAS
.
- J. Y. Kim, S. W. Ahn, S. S. Lee and J. M. Kim, Lab Chip, 2012, 12, 2807–2814 RSC
.
| This journal is © The Royal Society of Chemistry 2015 |