Rational design of nanoparticle/monomer interfaces: a combined computational and experimental study of in situ polymerization of silica based nanocomposites

Abstract

Interfaces between methylmethacrylate monomers, oligomers and silica nanoparticles (NPs) were explored by molecular dynamics simulations, infrared and solid state nuclear magnetic resonance spectroscopy. This knowledge allowed the control of the structure of the interfaces by employment of MMA macromonomers, and the design of an improved process for in situ polymerizations with a remarkable increase of NP dispersion.

---

Unique features, as well as improved physical properties, can be obtained for polymeric nanocomposites (PNCs) controlling the effects that the polymer/filler interactions have on the macromolecular chains, in terms of mobility, conformation, free volume, crystallinity, etc.^1–3 On this basis, the engineering and the design of polymer–nanoparticle interfaces are a fundamental tool to control the dispersion of nanoparticles (NPs) and modulate nanocomposite properties.

In the last decade the understanding of the dispersion of NPs in polymer matrices has made significant progress and theoretical approaches provided a general picture of the phase behavior of PNCs.^4–6 Complete phase diagrams can be obtained using integral equation theory approach applied to polymers (PRISM) in good agreement with several experiments.⁷ PRISM theory^8,9 predicts a stable NPs dispersion between a depletion-governed aggregation (for low interfacial attraction) and bridging aggregated states (for high interfacial attraction). Dispersion in PNCs can be controlled by surface modification of NPs. Enthalpic interactions are minimized when NPs are grafted using the same polymer or a polymer miscible with that employed as matrix.¹⁰ In this case, the strategy to control the NPs dispersion is mainly related to the variation of the grafting density and grafted chain length.^11,12 Several experimental and theoretical studies converge on a common accepted picture that particles with high grafting densities are miscible with a polymer matrix of the same chemistry, providing that the length of grafted chains is enough to intermingle with the matrix chains.^11,13 However, although these strategies allow to overcome filler/matrix chemical incompatibility and to control the interface, at the same time they often require multi step and advanced chemical processing.

A further key aspect of NPs dispersion is the preparation method of the PNC. Preparation methods can be classified according to the starting materials and processing techniques as blending, sol–gel and in situ polymerization.¹⁴ In situ polymerization methods involve the dispersion of the NPs in the monomer first; NPs can be treated before mixing with appropriate (chemical or physical) surface modifiers and then dispersed into monomer. Finally, monomers are polymerized using techniques similar to bulk polymerization.¹⁵ Among the numerous PNCs, polymer/silica nanocomposites have received much attention in the recent years and have been employed in a variety of applications; in situ preparation strategy has been widely applied to this class of PNCs.¹⁴ In particular, Kashiwagi et al.¹⁶ prepared PMMA/silica nanocomposites by in situ radical polymerization of MMA with colloidal silica. Improvement of silica NP dispersion has been achieved by chemical or physical modifications of NP's surfaces before in situ polymerization process. Through chemical modifications, Chen et al.¹⁷ incorporated three different types of modified silica particles in a PMMA matrix, proving that more hydrophobic particles are more compatible with the polymeric matrix. Other examples of chemical modification have been reported by Nakanishi et al.¹⁸ and Avolio et al.¹⁹ In particular, Nakanishi et al.¹⁸ prepared PMMA/silica hybrid materials incorporating reactive silica nanoparticles. Avolio et al.¹⁹ employed as modifier methacryloylpropyl trimethoxysilane grafted on silica NP surface characterized by a vinyl end group available to radical reactions. This modifier participates in the acrylic monomer polymerization producing an in situ NP grafting and assuring a good dispersion of nanoparticles as well as a strong nanoparticle/matrix interfacial adhesion. Physical modifications involve surfactant or macromolecule adsorption onto the surface of silica particles before in situ polymerization aimed to compatibilize the nanoparticle surface with both the initial monomer and the final polymerized bulk phases. For example, silica NPs were treated with cetyltrimethylammonium bromide (CTAB), stearic or oleic acid. Silica NPs have been also modified using both synthetic or natural macromolecules. Reculusa et al.^20–22 modified silica surface by adsorption of an oxyethylene-based macromonomer while Lu et al.²³ chose a natural biomacromolecule, chitosan, as an adsorbent to alter the surface properties of silica. More in general is high desirable to obtain strategies allowing to overcome filler/matrix incompatibility and to control the interface structure without complex chemical manipulations of NP surfaces.

Computer simulations are playing an increasing role in a detailed molecular understanding of interfacial regions of PNCs. Several studies, using Coarse-Grained (CG) models, of bulk polymers interacting with NPs, have been reported by many authors.^4,24–28 Moreover, several studies have been reported on MD simulations of realistic atomistic models of polymer chains in contact with nanoparticles. As an example, Barbier et al.²⁹ reported on the MD simulation of the interface between poly(ethylene oxide) and silica, Milano et al.³⁰ on MD simulations of the interphase structure and dynamics of polystyrene near bare and coated Au nanoparticles, and Müller-Plathe et al.³¹ on polystyrene–silica nanocomposite. More recently Eslami et al. reported MD simulations of a silica nanoparticle in oligomeric poly(methyl methacrylate) (PMMA).³² The level of detail in the description of chemical structures in this type of simulations is useful to give indications and eventually to improve the preparation process.

With these precedents, the aim of this communication is twofold. First molecular insights on the interfaces between silica NP and the bulk monomer phase are provided. In particular, by a combined use of atomistic MD simulations and experimental characterization, the behavior of methylmethacrylate monomer (MMA) and oligomers (PMMA)_n at the surface of silica NPs was explored. Then, this knowledge allowed us to design and control the structure of the interfaces. In particular, exploiting the self-assembly properties of MMA macromonomers (MMA)_n, near silica surface, targeted experiments have been performed to improve in situ polymerization process.

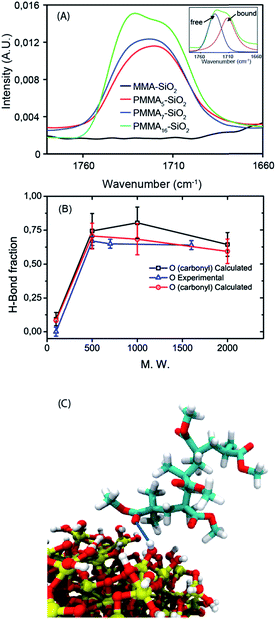
In Fig. 1 the density isosurface of hydrogen bond donors (–OH groups) present on the silica NP surface (in red) calculated from MD simulation is depicted. The picture is representative of both NP/MMA and NP/PMMA systems, because the density of –OH groups is dictated by the bond scheme on NP surface that is the same in both cases. Very different is the behavior of hydrogen bond acceptors (both oxygen types in MMA and PMMA structures) spatial distribution around the NP (depicted in blue). In this case, as schematized on the right side of Fig. 1, although the monomer and oligomer chemical structures are very similar (from the modeling point of view σ, ε parameters and partial charges characterizing non bonded interactions of oxygen atoms on MMA and PMMA are identical), from the figure it is clear that in the vicinity of NP surface in the case of NP/MMA monomer interface the presence of HB acceptor is very low. On the contrary, in the case of PMMA oligomer the region close to the NP surface is rich of oxygen atoms. This feature is confirmed by radial density profiles for both systems in Fig. 1A: the radial density of MMA monomers around the NP is always much lower than the bulk monomer density (about one half), while for the all considered PMMA oligomers the radial density shows a maximum or a value comparable with the PMMA bulk density. A peculiar feature of the system under investigation is the possibility of hydrogen-bond (HB) formation between the hydroxyl group on the NP surface and oxygen atoms of MMA and PMMA. In Fig. 1B the HB fraction between the NP hydroxyl groups and the oxygen atoms as function of molecular weight is shown. It is worth noting that, in the case of the MMA, for both temperatures, the calculated HB fraction is close to zero, while for all considered PMMA oligomers is around 0.25. As expected, the main contribution to HB comes from carbonyl oxygen, while ester oxygen are involved in HB at lower extent. The weak dependency on molecular weight of both density profiles and H-bond fraction values for PMMA oligomers are in good agreement with calculated values of Eslami et al.³² The absence of HB can be ascribed to entropic effects. In particular, in the case of MMA a loss of translational entropy, due to NP surface anchoring can be hypothesized. Different is the case of polymer PMMA chains, dominated by conformational entropy slightly altered by surface anchoring. To verify the simulations findings, the occurrence of interactions between PMMA oligomers and SiO₂ surface was proved through absorption experiments. In particular, nanoparticles were suspended into PMMA_n solutions in toluene and the adsorbed fractions, PMMA_n–SiO₂, were recovered after purification, as discussed in the ESI.‡ Fig. 2 presents FTIR spectra in the carbonyl region of PMMA_n–SiO₂. As known, hydrogen bounded carbonyls give rise to an absorption band at lower wavenumber than non-interacting carbonyl groups, free carbonyls, thus allowing to determine interactions between PMMA_n and silica.³³

Fig. 1 On the top, density isosurfaces of –OH groups on the silica NP (red surfaces on the left side), and of oxygens atoms acceptors of hydrogen bond for MMA and PMMA (blue surfaces), respectively system 1 and 4 in Table S10 of ESI.‡ Isosurfaces have been calculated in a sphere centred on the NP center of mass having a radius of 2.0 nm. The isosurfaces include regions where density ρ is larger than ρ* (where ρ* is 0.35 times the bulk density). For a direct comparison with experiments, radial density profiles for MMA and PMMA of different molecular weights (A) have been calculated at 20 °C. The same has been done for HB fractions (B) calculated as function of molecular weight for carbonyl (black curve) and for ester (red curve) oxygen atoms. The behaviour of both properties at 80 °C (in situ polymerization temperature) is very similar and have been reported in the ESI.‡ In the panel on the right are reported the chemical structures of monomer MMA and polymer PMMA. The H-B count is based on geometrical criteria. An H-bond is counted if the distance H–O is shorter than 0.3 nm, and the angle θ_HOH between OH–O (acceptor) is greater than 120°. Initial configurations, suitable for MD simulations, have been obtained for all systems using an extension of the procedure reported in ref. 34. More details about the relaxation procedure are reported in the ESI.‡ section.

Fig. 2 (A) FTIR spectra of PMMA_n–SiO₂ in the carbonyl region. An example of curve fit is reported in the onset. (B) HB fractions for systems calculated in vacuo (black curve, obtained including PMMA_n chains forming at least one H-B in the bulk, and red curve, including the number of PMMA_n chains per nm² found in TGA experiments) curves and obtained from FTIR (blue curve) as function of molecular weight. (C) Snapshot of a chain of PMMA₅, for the system calculated in vacuo, forming a H-bond with silica–OH group.

In this spectral region, no absorption bands are detectable for MMA–SiO₂ thus indicating that the monomer is not interacting with the silica surface. In the case of PMMA₅–SiO₂ and PMMA₇–SiO₂, the spectra present a complex broad band^35,36 centred at around 1720 cm⁻¹ while for PMMA₁₆–SiO₂ it is clearly observable that this broad band is constituted by two partially convoluted peaks centered at around 1730 cm⁻¹ and 1714 cm⁻¹, respectively. To estimate the interacting fraction, the carbonyl bands of all samples were resolved in two components using a mixed Gauss–Lorentz function, as illustrated in the onset of Fig. 2. These evidences demonstrate that PMMA oligomers are able to interact with silica surface via hydrogen bonding involving OH groups of SiO₂ and carbonyl moieties of PMMA_n chains. The bound fraction (BF) was calculated by using eqn (S6‡) reported in the ESI.‡

As shown in Fig. 2B and summarized in Table S11 (reported in ESI‡), the BF values calculated are almost constant and independent of the molecular weight. Then, the amount of PMMA_n adsorbed onto silica nanoparticles, Ads, was evaluated by TGA and expressed as mg of PMMA_n per square meter of silica surface (see Table S11‡). A significant amount of adsorbed organic fraction was measured in the case of PMMA_n oligomers showing comparable Ads values. On the contrary, the adsorbed fraction of MMA monomer is so small that no distinguishable signals were evidenced in the corresponding FTIR spectrum. These findings are in qualitative agreement with the results of simulations (calculated H-bond data) reported in Fig. 1.

In order to compare in more quantitative way calculated and FTIR data, MD simulations were run “in vacuo” retaining only the chains forming at least one HB with NP surface from systems simulated in the bulk. This assumption can be validated considering that the quantity of adsorbed chains per nm² obtained by TGA experiments is close to the number of chains forming at least one HB. In fact, comparing Fig. 1B and 2B it is clear that in all considered range of molecular weight the calculated H-bond fraction, due to a lower amount of interchain interactions, is higher than in bulk systems and close to the experimental values. Moreover, in the case of oligomers the tendency to form H-bond with the NP is high and nearly constant.

On this basis, the challenge to design the interface in PMMA/silica nanocomposite, exploiting H-bond interactions involving silica and PMMA_n oligomers was explored. In particular, it was verified the intriguing possibility to start the in situ polymerization from a different scenario in which particle surface is expected to be well wetted because more interacting with the organic phase. Following this main idea MMA_n polymerizable macromonomers were synthesized according to a literature procedure.³⁷ In particular the MMA₄ (tetramer 2,4,6,8-tetrakis (methoxycarbonyl)-4,6,8-trimethy non-1-ene, see Scheme 1) was obtained by radical polymerization of MMA in the presence of the cobalt(III) complex (iPr)(H₂O)CoIII-(DMG-BF₂)₂ and subsequent fractionation of the reaction mixture by vacuum distillation. The aim was to prepare PMMA/silica nanocomposite through the in situ polymerization approach starting by a mixture of MMA monomer and MMA₄ unsaturated macromonomer more interacting with the silica surface due to its longer chain length and to verify the effect of this procedure on the NP dispersion. In detail, the idea was that polymerizable macromonomer is able to participate to radical polymerization and at the same time could better interact with both organic phase and NP surface, as above demonstrated in the case of saturated oligomers with similar molecular weight, forming a high density shell around the particles. A preliminary characterization of NP–macromonomer interaction has been performed before polymerization runs. In particular, it was firstly confirmed that the MMA₄ interacts strongly than MMA monomer with silica NP surface performing adsorption analysis, according to the same experimental procedure described above. FTIR analysis confirmed a high hydrogen bonded fraction (BF = 0.94) while a low Ads value, 0.22 mg m⁻², about one half with respect to values calculated for the other oligomers, was determined by TGA. The low absorbed fraction could be ascribed to the different solubility in toluene of the macromonomer due to the presence of a double bond as compared to the PMMA_n saturated oligomers.³⁸

Scheme 1 Saturated MMA oligomers PMMA_n and polymerizable MMA macromonomers MMA_n.

On the basis of the strong MMA₄–silica NP interactions, nanocomposite containing 1 wt% of silica NP was synthesized starting from a mixture of MMA and MMA₄ detailed in the ESI.‡ To understand the role of MMA₄ in the in situ polymerization process, for comparison, PMMA nanocomposite obtained through the radical polymerization of pure MMA (i.e. without inclusion of any macromonomer) was also prepared.

After polymerization, both nanocomposites were suspended in toluene to recover the insoluble silica-rich fractions, coded P(MMA)–SiO₂ and P(MMA-co-MMA₄)–SiO₂, that were purified and analyzed by FTIR to evaluate the possible formation of an interacting interphase. FTIR spectra evidenced typical features of the organic phase in both insoluble fractions, however, in the case of (PMMA-co-MMA₄)–SiO₂ the shape of carbonyl peak suggests the presence of an interacting fraction. In fact, the BF value calculated for this fraction is 0.39 while for P(MMA)–SiO₂ this value is negligible (BF = 0.02). ¹³C solid state NMR was also performed on the (PMMA-co-MMA₄)–SiO₂. The spectrum, reported in the ESI,‡ shows the signals of PMMA moieties, in agreement with the results of the FTIR spectroscopy. The very interesting finding is the absence of any signal ascribable to vinyl PMMA end groups proving that the more interacting MMA₄ macromonomer quantitatively participates to the radical polymerization. Moreover comparing this spectrum with that of a PMMA oligomer (PMMA₁₆), the resonance of terminal –OCH₃ carbons was identified at 41.5 ppm. The integration of this peak allows to determine an approximate molecular weight of the interacting chains of 8000 Da. In Fig. 3 TEM micrographs of nanocomposites are reported. To discuss the morphology of these materials, it's worth to remind the complex structure of fumed silica. In particular, the predominant structure of fumed silica consists of fractal-like aggregates, formed by firmly attached and partially fused primary particles. In our systems, an enhancement in silica dispersion in the nanocomposite obtained in the presence of MMA₄ macromonomer with the reduction of aggregate size was clearly evidenced by TEM micrographs, as reported in Fig. 3. Image analysis of the collected TEM micrographs showed that for the nanocomposite obtained from neat MMA (Fig. 3A) the mean area of the 2D projections (A_2D) of the silica agglomerates is about 2550 nm², with a maximum A_2D value of 21 000 nm², whereas these values decreased to a mean A_2D value of about 1700 nm², with a maximum A_2D of 7000 nm², for the agglomerates evidenced in the material obtained from MMA/MMA₄ mixture. This can be ascribed to the formation, in the last case, of an interacting organic shell able to avoid the clustering of the original fumed silica agglomerates.

Fig. 3 Bright field TEM micrographs of nanocomposites obtained by in situ polymerization of: (A) pure MMA monomer; (B) MMA/MMA₄ mixture. Image analysis gave mean area of the 2D projections of the silica agglomerates of about 2550 nm², with a maximum A_2D value of 21 000 nm² for (A) whereas these values decreased to a mean A_2D value of about 1700 nm², and a maximum A_2D of 7000 nm² for (B).

Conclusions

Summarizing, an approach combining atomistic MD simulations and experiments demonstrated that it is possible to enhance the interactions between bulk monomer and NP surfaces playing only on the molecular weight of the monomers and avoiding any NP's surface modification. The idea is that by simply changing MMA/(MMA)₄ ratio in the polymerization mixture a modulation of density of adsorbed organic phase could be obtained thus guiding the interphase density and chain length. This finding is particularly promising and could represent a new tool for the control and the design of the PNC interface structure and properties as well as for the modulation of bulk PNC properties and more in general on the complementarity between simulation and experiments for the interpretation of complex physicochemical phenomena and the design of new materials.

Acknowledgements

G. M. thanks MIUR (FIRB “RETE ITALNANONET”) for financial support. ​C. C. and M. E. thank MIUR (PRIN-“Materiali polimerici nanostrutturati con strutture molecolari e cristalline mirate, per tecnologie avanzate e per l'ambiente”, National Grant PRIN 2010XLLNM3_006). The computing resources and the related technical support used for this work have been provided by CRESCO/ENEAGRID High Performance Computing infrastructure and its staff.³⁹ CRESCO/ENEAGRID High Performance Computing infrastructure is funded by ENEA, the Italian National Agency for New Technologies, Energy and Sustainable Economic Development and by Italian and European research programmes, see http://www.cresco.enea.it/english for information.

Notes and references

1. V. Ganesan and A. Jayaraman, Soft Matter, 2014, 10, 13–38.
2. R. Krishnamoorti, MRS Bull., 2007, 32, 341–347.
3. D. Schmidt, D. Shah and E. P. Giannelis, Curr. Opin. Solid State Mater. Sci., 2002, 6, 205–212.
4. G. Allegra, G. Raos and M. Vacatello, Prog. Polym. Sci., 2008, 33, 683–731.
5. G. Raos and J. Idé, ACS Macro Lett., 2014, 3, 721–726.
6. J. Jancar, J. F. Douglas, F. W. Starr, S. K. Kumar, P. Cassagnau, A. J. Lesser, S. S. Sternstein and M. J. Buehler, Polymer, 2010, 51, 3321–3343.
7. Y. N. Pandey, G. J. Papakonstantopoulos and M. Doxastakis, Macromolecules, 2013, 46, 5097–5106.
8. A. P. Chatterjee and K. S. Schweizer, J. Chem. Phys., 1998, 109, 10464–10476.
9. S. Y. Kim, K. S. Schweizer and C. F. Zukoski, Phys. Rev. Lett., 2011, 107, 225504.
10. Y. Li, T. M. Krentz, L. Wang, B. C. Benicewicz and L. S. Schadler, ACS Appl. Mater. Interfaces, 2014, 6, 6005–6021.
11. S. K. Kumar, N. Jouault, B. Benicewicz and T. Neely, Macromolecules, 2013, 46, 3199–3214.
12. D. Maillard, S. K. Kumar, A. Rungta, B. C. Benicewicz and R. E. Prud'homme, Nano Lett., 2011, 11, 4569–4573.
13. M. Asai, A. Cacciuto and S. K. Kumar, Soft Matter, 2015, 11, 793–797.
14. H. Zou, S. Wu and J. Shen, Chem. Rev., 2008, 108, 3893–3957.
15. V. Mittal, In-situ Synthesis of Polymer Nanocomposites, Wiley, 2011.
16. T. Kashiwagi, F. Du, J. F. Douglas, K. I. Winey, R. H. Harris and J. R. Shields, Nat. Mater., 2005, 4, 928–933.
17. Y.-H. Hu, C.-Y. Chen and C.-C. Wang, Polym. Degrad. Stab., 2004, 84, 545–553.
18. H. Sugimoto, K. Daimatsu, E. Nakanishi, Y. Ogasawara, T. Yasumura and K. Inomata, Polymer, 2006, 47, 3754–3759.
19. R. Avolio, G. Gentile, M. Avella, D. Capitani and M. E. Errico, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 5618–5629.
20. S. Reculusa, C. Poncet-Legrand, S. Ravaine, C. Mingotaud, E. Duguet and E. Bourgeat-Lami, Chem. Mater., 2002, 14, 2354–2359.
21. S. Reculusa, C. Poncet-Legrand, A. Perro, E. Duguet, E. Bourgeat-Lami, C. Mingotaud and S. Ravaine, Chem. Mater., 2005, 17, 3338–3344.
22. A. Perro, S. Reculusa, E. Bourgeat-Lami, E. Duguet and S. Ravaine, Colloids Surf., A, 2006, 284–285, 78–83.
23. X. Yang, T. Dai, M. Wei and Y. Lu, Polymer, 2006, 47, 4596–4602.
24. H. Chen and E. Ruckenstein, Polymer, 2010, 51, 5869–5882.
25. H. Chen and E. Ruckenstein, J. Chem. Phys., 2009, 131, 244904.
26. A. Ghanbari, T. V. M. Ndoro, F. Leroy, M. Rahimi, M. C. Böhm and F. Müller-Plathe, Macromolecules, 2011, 45, 572–584.
27. A. Ghanbari, M. Rahimi and J. Dehghany, J. Phys. Chem. C, 2013, 117, 25069–25076.
28. F. A. Detcheverry, H. Kang, K. C. Daoulas, M. Müller, P. F. Nealey and J. J. de Pablo, Macromolecules, 2008, 41, 4989–5001.
29. D. Barbier, D. Brown, A.-C. Grillet and S. Neyertz, Macromolecules, 2004, 37, 4695–4710.
30. G. Milano, G. Santangelo, F. Ragone, L. Cavallo and A. Di Matteo, J. Phys. Chem. C, 2011, 115, 15154–15163.
31. T. V. M. Ndoro, E. Voyiatzis, A. Ghanbari, D. N. Theodorou, M. C. Böhm and F. Müller-Plathe, Macromolecules, 2011, 44, 2316–2327.
32. H. Eslami, M. Rahimi and F. Müller-Plathe, Macromolecules, 2013, 46, 8680–8692.
33. R. R. Madathingal and S. L. Wunder, Langmuir, 2010, 26, 5077–5087.
34. A. De Nicola, T. Kawakatsu and G. Milano, Generation of Well Relaxed All Atom Models of Large Molecular Weight Polymer Melts: A Hybrid Particle-Continuum Approach Based on Particle-Field Molecular Dynamics Simulations, J. Chem. Theory Comput., 2014, 10(12), 5651–5667.
35. M. T. Kabomo, F. D. Blum, S. Kulkeratiyut, S. Kulkeratiyut and P. Krisanangkura, J. Polym. Sci., Part B: Polym. Phys., 2008, 46, 649–658.
36. S. Kulkeratiyut, S. Kulkeratiyut and F. D. Blum, J. Polym. Sci., Part B: Polym. Phys., 2006, 44, 2071–2078.
37. C. L. Moad, G. Moad, E. Rizzardo and S. H. Thang, Macromolecules, 1996, 29, 7717–7726.
38. A. V. Bailey, J. A. Harris and E. L. Skau, J. Chem. Eng. Data, 1970, 15, 583–585.
39. G. Ponti, HPCS 2014, 2014, art. no. 6903807, 6901030–6901033.

---

Footnotes

† Dedicated to the memory of Adolfo Zambelli.

‡ Electronic supplementary information (ESI) available: Experimental conditions, computational methods, models parameters and supplementary results are reported. See DOI: 10.1039/c5ra13154e

§ Both of these authors contributed equally to this work.

---