Dielectric environment as a factor to enhance the production yield of solvent exfoliated graphene

Abstract

High yield production of high quality graphene is essential for its application in electronics, optoelectronics and energy storage devices. Liquid phase exfoliation based methods for obtaining graphene are becoming popular because of their versatility and scalability. These advantages are absent with other growth methods such as mechanical exfoliation using scotch tape and chemical vapor deposition. Here we present a sonication assisted, surfactant free method for liquid phase exfoliation of graphene using solvents with varying dielectric constants. We have shown that the method presented here is capable of producing high yields (1.22 wt%), and exceptionally large sizes (30–50 microns) with a high carrier mobility of 10 000 cm² Vs⁻¹ in monolayer graphene. Moreover, it is possible to obtain pristine as well as doped monolayer or bilayer or multilayer graphene with extreme controllability, on any solid substrate. It has been shown that choice of a solvent of a particular dielectric constant and sonication time are key parameters for liquid phase exfoliation. It is further shown that the exfoliation efficiency can be enhanced using solvents with high dielectric constant due to functionalization which has also been supported by density functional theory based electronic structure calculations. We have also tested this fact by using different solvents with similar dielectric constant. This method promises high-end industrial scale synthesis for potential applications in different types of devices, graphene based composites and liquid phase chemistry as well.

---

Introduction

Graphene,^1,2 a two dimensional atomic layer of carbon atoms has attracted tremendous interest due to its remarkable properties such as ambipolar field effect,¹ room temperature quantum hall effect³ and extremely high charge carrier mobility.⁴ However, similar to the problems in the growth of carbon nanotubes⁵ and nanowires⁶ in the early days, the production of graphene also lacks a method which is scalable and controllable. There are two different approaches adopted for obtaining graphene monolayers: top down and bottom up. In the former case, mechanical exfoliation¹ is the most popular method to obtain graphene with the highest quality. However, the fraction of graphene monolayers remains negligible among the thick graphitic flakes. In addition to this, it is difficult to envisage how to scale up mechanical exfoliation method for mass production of graphene layers. Alternatively, graphene has been grown on solid substrates using bottom up method such as chemical vapor deposition^7,8 (CVD) and surface modification of SiC.⁹ Although these methods are capable of producing large area graphene but it requires transfer of as grown graphene on desirable substrates, either by mechanical transfer or by solution processing, which is cumbersome and eventually leads to degradation of graphene layers. Graphene grown by annealing of SiC generally has multiple domains, which are not spatially uniform over larger length scales. Moreover, the controllability of these methods is rather poor. Chemical methods^10–12 are the viable routes to produce graphene in large quantities. Several works have been published on dispersion of graphene oxide (GO),^10,13,14 which contains graphene like sheets but its properties get severely perturbed due to uncontrolled functionalization with various chemical functionalities. Highest mobility of few thousand units has been obtained till today in chemically synthesized graphene monolayer. Unless the concentration of defects is controlled so that mobility of carriers is comparable to that in case graphene is synthesized by exfoliation based techniques, chemical methods will survive only for academic interest. Hernandez et al.¹⁵ demonstrated how to produce graphene layers using chemical exfoliation of graphite. They have shown that yield of graphene monolayers can be controlled by choosing appropriate solvents whose surface energies matches with that of graphite. But their approach does not shed light on how to control the quality and size of the graphene films, which are the important parameters in the context of its future applications. Generally, chemically assisted techniques^13–15 for growth of graphene suffer from a significant disadvantage: uncontrolled oxidation of graphene layers resulting formation of structural defects which can be seen in Raman spectra as an intense D band at 1350 cm⁻¹. Thus a feasible method that is capable of growing graphene with excellent controllability on quality, size and production yield is required. In this article, we present a detailed investigation on sonication-assisted, surfactant free, liquid phase exfoliation (LPE) method that has potential to be the most suitable method for large scale production of graphene. We have shown that high yield of graphene monolayers (up to 1.22 wt%) can be achieved by solvents with high dielectric constant. It has been observed that in addition to monolayer number fraction or yield, the size of the graphene layers can be controlled by sonication time during exfoliation.

Experimental

Synthesis of graphene

The graphene layers were grown by LPE method using several organic solvents with different dielectric constant (k) such as toluene (k ∼ 2.5), chlorobenzene (k ∼ 5.4), acetone (k ∼ 17.7), acetonitrile (k ∼ 37), N,N-dimethylformamide or DMF (k ∼ 38) and propylene carbonate or PC (k ∼ 64). Fig. 1 shows schematic illustration of the LPE method. Briefly, graphene layers were obtained by sonicating a piece of highly ordered pyrolytic graphite (HOPG) in different solvents with initial concentration of 0.06 mg ml⁻¹. This exfoliation method consists of 2 steps: (i) sonication of HOPG in particular solvent (8–12 hours), (ii) centrifugation of sonicated solution (2 hours) in order to precipitate out thick graphitic layers. The solvents and a piece of HOPG were sonicated using ultrasonic bath at 80% of maximum power and temperature of the bath tank was maintained below 45 °C in order to avoid excess heating. The adjacent graphene layers in bulk graphite are held together due to the presence of weak van der Walls attractive forces among them. So during sonication when surface energy of liquid medium matches that of graphitic surfaces it will separate out into thin layers in the form of dispersion. Thus, after sonication, resultant dispersion was then centrifuged using swinging head centrifuge. Just after centrifugation, solution containing thin graphene layers (from top half of the solution) was pipetted off on desired substrates (SiO₂/Si, quartz, sapphire etc.). Thickness of SiO₂ was chosen 300 nm in order to get better optical contrast. Initial sample drying was carried out in vacuum at room temperature at a pressure of ∼10⁻³ mbar. Then vacuum dried samples were annealed at ∼200 °C, preferably above boiling point of solvents for 30 minutes in vacuum before further characterizations.

Fig. 1 Schematic diagram of chemical exfoliation method. Snapshots of sonicated and centrifuged solutions are also given.

Measurement set-up & device fabrication

Raman spectroscopy was done using WITec GmbH Raman microscope with 50× objective and excitation wavelength of 532 nm. Park Systems, XE-70 model in non contact mode was employed for atomic force microscopy (AFM). AFM images were taken on graphene supported on SiO₂ (300 nm)/Si substrates. A TEM (model – JEOL-2100F) investigation (HRTEM image and diffraction pattern) of single and multilayer graphene were acquired using carbon coated holey grids. The microscope was operated at acceleration voltage of 200 KV. Field effect transistors were fabricated on SiO₂ (300 nm)/Si (n⁺⁺) in bottom gate configuration, metal electrodes were patterned using electron beam lithography followed my metal (Cu) deposition. All electrical measurements were done in vacuum (10⁻³ mbar). Keithley 228A voltage source, Agilent N5752A voltage source and Keithley 6485 picoammeter were used for electrical measurement. UV-Vis absorption spectroscopy and transmittance measurement was done on quartz or sapphire substrates using Shimadzu UV-2401 PC spectrophotometer.

Results and discussions

We have exfoliated graphene layers from HOPG by sonicating in several solvents.

Homogeneous dispersion with graphene layers were separated from black dispersion consisting of large number of suspended macroscopic aggregates by centrifugation (Fig. 1). Snapshots of such dispersions prepared from different graphite concentrations are shown in Fig. 2a. It has been observed that exfoliation efficiency and separation of thick graphitic flakes strongly depend on sonication and centrifugation times, respectively. Yield of the exfoliation is basically determined by the concentration of remaining dispersed phase after centrifugation because it only includes thin graphene layers. In order to find the concentration after centrifugation we passed the graphitic dispersion through polyamide membrane filters from Sigma Aldrich (pore size: 200 nm). These dispersions were then characterized by UV-visible absorption spectroscopy (Fig. 2a). As expected, the spectra are featureless in the visible region. These dispersions were then diluted number of times and absorption spectra were recorded. Absorbance (at 660 nm) divided by cell length is plotted against diluted concentrations, showing Beer–Lambert behaviour for graphene dispersions in various solvents with α ∼ 1200 Lg⁻¹ m⁻¹ (Fig. 2b), here α is the molar absorptivity and related to the optical absorbance as¹⁶ A/l = α × C, where, A is optical absorbance; l, cell length; and C, concentration of the dispersion. As discussed above, remaining fraction of the sediments after centrifugation is very important parameter to describe the exfoliation efficiency. We have tried to disperse HOPG in different solvents and the remaining fraction (δ) after centrifugation was calculated from measured absorption coefficient and average molar absorptivity at 660 nm (α₆₆₀) ∼1200 L gm⁻¹ ml⁻¹. Fig. 2c illustrates concentration of remaining sediments after centrifugation as a function of surface energies of respective solvents. In case of toluene and chlorobenzene we have observed relatively low fraction of remaining sediments (∼3–4%) whereas, for acetone, DMF and PC, relatively high fraction of remaining sediments (∼5–8%) was observed. Variation in δ with surface energies of the solvents follows linear relationship. Moreover, Fig. 2d illustrates that yield of graphene monolayers increases linearly with polarity of the solvents. This linear variation in δ and yield will be discussed later in this article. Fig. 3 provides some examples of transmission electron microscopy (TEM) images and specific area electron diffraction patterns (SAED) acquired on graphene layers. These TEM images indicate that suspended graphene layers are not perfectly flat and they exhibit microscopic corrugations/roughening in order to be thermodynamically stable. In addition to imaging of the graphene flakes using TEM, we could directly differentiate the monolayer and multilayer graphene by analyzing SAED patterns,¹⁷ which allowed us to probe the graphene's reciprocal space which has hexagonal structure.¹⁷ The key for the identification of graphene monolayer is that its reciprocal space should have only zero order Laue zone, therefore one should observe uniform intensity of diffraction patterns.¹⁷ For multilayers, diffraction patterns vary according to the stacking sequence of the graphitic flakes. Fig. 3a and b show TEM images of graphene layers exfoliated in low k solvents and insets show the electron diffraction patterns corresponding to circled areas. As expected, there exist six fold uniform and symmetric spots, which are the signature of monolayer graphene. Fig. 3c illustrates TEM image of monolayer graphene exfoliated in high k solvent and its diffraction pattern is given in Fig. 3f as indicated by an arrow.

Fig. 2 (a) Absorption spectra for graphene based dispersions in PC, toluene, DMF and acetone at concentrations from 1.5 to 7 μg ml⁻¹. Inset shows snapshots of graphene based dispersions in toluene, at a range of concentrations ranging between 2 and 6 μg ml⁻¹. (b) Optical absorbance (at λ = 660 nm) divided by cell length (A/l) plotted against concentration of graphene in four solvents as mentioned above. Spectra shows Beer–Lambert behaviour with molar absorptivity of α (660) = 1200 Lg⁻¹ m⁻¹. X-axis error bars denote uncertainty in measuring graphite masses in solution after centrifugation. (c) Concentration of remaining sediments after centrifugation as a function of surface energies of respective solvents. (d) Production yield as a function of dielectric constant of the solvents used for exfoliation (see ESI† for details). Symbols are the data points and solid line is linear fit to the data.

Fig. 3 TEM imaging and corresponding SAED pattern acquired on graphitic/graphene flakes obtained by LPE of HOPG. (a–c) TEM images of graphene layers obtained by exfoliation of HOPG in different solvents and inset shows SAED pattern of monolayer graphene with six bright spots corresponding to the encircled area. SAED patterns show (d) randomly stacked multilayered graphene/graphite with slightly rotated diffraction spots indicating polycrystalline behavior. (e) Bernal stacked (AB) graphene bilayer with planes in a certain arrangement (indicated by arrows). (f) Diffraction pattern of a monolayer graphene flake showing uniform intensity diffraction spots arranged in a hexagonal pattern. Schematic representation of (g) Bernal stacked graphitic flakes and (h) random stacking of graphene multilayers. Circles indicate approximate regions where electron diffraction was acquired. Scale bars (a–b): 1 μm; (c): 500 nm.

Fig. 3a and b also contains multilayer graphene flakes whose electron diffraction patterns are given in Fig. 3d and e which corresponds to randomly stacked and Bernal stacked multilayer graphene, respectively. Fig. 3g and h provide schematic illustration of Bernal stacked^15,17 and randomly stacked graphene multilayers. Bernal stacking of multilayers indicates thick ordered graphitic flakes that were never exfoliated whereas, random stacking suggests that they did exfoliate but re-aggregated in the dispersion phase. AFM was carried out to determine the size, morphology and thickness of the exfoliated graphene layers. Fig. 4a and b show AFM images of such exfoliated graphene layers with size >10 microns for each. Thickness profile indicates the height of 0.6 nm for monolayer and 1.2 nm for bilayer graphene with excellent uniformity. Several AFM images were recorded and examined in order to obtain a statistics of size distribution and number fraction for graphene layers. Fig. 4c shows size distribution of graphene layers as function of their respective thickness as obtained from AFM. Relatively thin layers have larger sizes up to 10 microns for monolayers and 35 microns for few layer (<5) graphene.

Fig. 4 Atomic force microscopic images of graphene layers obtained by exfoliation of HOPG in (a) toluene and (b) PC. Respective height profiles are also given and indicated by arrows. (c) Histogram showing size distribution of graphene flakes as a function of their respective thickness as observed by AFM. Data corresponds to dispersions sonicated for 12 hours. (d) Size of monolayer graphene as a function of sonication time. It indicates that average size of the graphene flakes varies inversely with the sonication time. Y-axis error bars denote variation in flake sizes over 10–20 flakes. Circles denote the data points and solid line is the linear fit.

Thin flakes have relatively small sizes, which suggest that large area thick graphite flakes have been efficiently exfoliated to produce monolayer graphene. Since, LPE is assisted by sonication, which may cause cutting of graphene flakes; we have also monitored the effect of sonication on the size distribution of graphene layers. We have exfoliated graphene layers under three different sonication times. Fig. 4d summarizes the effect of sonication on the size of graphene monolayers. It is clearly visible that as we reduce the sonication time (t_s) from 12 to 8 h, size of the monolayers increases from 10 to 35 microns. The linear fit to the data indicates that size of the graphene monolayers vary inversely proportional to t_s. This is very important observation in order to achieve required size of graphene layers using LPE. Fig. 5 shows TEM images of large area (∼35 microns each) graphene layers obtained at t_s = 8 h. As discussed earlier in this article, SAED patterns corresponding to encircled areas indicate monolayer graphene whereas last SAED pattern corresponds to the folded graphene. It corroborates the flake size distribution extracted from the AFM measurements. Similarly, by monitoring several AFM images and their respective height profiles, we estimated number fraction of graphene layers.

Fig. 5 TEM images of large area graphene samples obtained by LPE of HOPG in (a) toluene and (b) DMF. SAED patterns corresponding to encircled areas are also given (c–e) and indicated by arrows. In (c–d), SAED patterns clearly show that these flakes are predominantly monolayers whereas; (e) shows SAED patterns corresponding to folded graphene monolayer with slightly rotated diffraction spots.

It is worth mentioning that one or two unnoticed large thick flakes with relatively higher mass will disturb the whole statistics hence extreme care has been taken while acquiring the AFM images, especially in case of large flakes. Fig. 6 illustrates number of visual observations of graphene flakes (number fraction) as a function of number of layers. It is evident from the histogram that, when the sonication time and centrifugation time were kept around 8 hours and 2 hours respectively, the number fraction of monolayer graphene was about 2–5% for most of the dispersions. We have observed significant difference in the number fraction of graphene monolayer that increases drastically (up to ∼25%) as we increase sonication time from 8 to 12 hours while keeping centrifugation time fixed for 2 hours. This suggests that, further exfoliation of few layer graphene due to extended sonication, results in high throughput of graphene monolayers. Monolayer mass fraction obtained from various graphene dispersions varied between 10–16 wt% leading to an overall yield between 0.4–1.22 wt% (see Table I in ESI†). Method to calculate mass fraction and production yield is given in ESI Section S1.0.†

Fig. 6 Histogram showing occurrence (number of visual observations) of graphene layers at sonication time (t_s) of 8 hours and 12 hours for graphene based dispersions in (a and b) toluene; (c and d) DMF and (e and f) PC. Data illustrates that with increase in sonication time from 8 to 12 hours, number fraction of monolayer graphene increases drastically from ∼4–25%.

It is essential to investigate the mechanism that facilitates the exfoliation of graphite in liquid media for better understanding of such sonication assisted LPE methods. Hernandez et al.¹⁵ suggested that, for LPE to occur, net energy cost (enthalpy of mixing per unit volume) should be very small. In this case, enthalpy of mixing ΔH ∝ (S_graphite − S_solvent)², where S_graphite and S_solvent are the surface energies of graphite and solvents, respectively. For graphite, the surface energy is defined as the energy per unit area required to overcome the van der Waals forces when peeling two graphene sheets apart. It is clear that minimal energy will cost for exfoliation, if surface energy of the solvents, matches with that of graphite. Hence, this criterion provides a rough guidance to select appropriate solvents for exfoliation of graphene layers. There are two observations firstly; all the solvents (toluene, chlorobenzene, acetone, DMF and PC) used for exfoliation have their surface energy values in the range of 40–90 mJ m⁻², which is the range of the surface energy reported for graphite.¹⁵ Hence, if surface energy of the solvents is solely governing the exfoliation mechanism then in this range we should have observed almost similar value of δ i.e. remaining fraction of sediments after centrifugation in all cases. In contrast, as discussed before, Fig. 2c shows linear variation in δ with surface energy of solvents. It suggests that some other parameter is responsible for such linear variation of δ with surface energies, leading to high production yield. So, we propose that it is dielectric constant of the solvents that plays an important role in exfoliation mechanism (see Fig. 2d). During sonication process, exfoliated graphene layers get strongly functionalized in high k solvents while weak functionalization was observed for low k solvents (see discussion on Fig. 7 and ESI S2.0†). It has been reported earlier^18,19 that surface chemistry can be altered with functionalization of solid surfaces. In this case, functionalization of the graphitic surfaces during sonication in high k solvents causes increase in exfoliation efficiency. Hence, as we increase the dielectric constant of the solvents, δ as well as production yields increases linearly. Further, we have tested this fact by using acetonitrile (k ∼ 37) which has dielectric constant close to that of DMF. It has been observed that in spite of substantial difference of almost 10 mJ m⁻² in surface energies, overall yield of graphene monolayers remain same when exfoliated in DMF and acetonitrile. Moreover, irrespective of similar surface energies for chlorobenzene, DMF and acetonitrile, substantial variation in production yield can be observed (see Fig. 2d and Table I in ESI†). These observations clearly suggest the importance of dielectric constant of the solvents for graphite exfoliation to achieve high fraction of monolayers.

Fig. 7 (a) Raman spectra of graphene layers. It is exfoliated in toluene, chlorobenzene, DMF and propylene carbonate (PC). In toluene and chlorobenzene, negligible D peak intensity has been observed whereas; in DMF and PC considerable D band intensity can be seen. Significant D band is attributed to the functionalization of graphene layers in high k solvents (DMF and PC). (b) Infrared spectra of graphene exfoliated in high k solvents (PC and DMF). (c) Schematic of graphene based field effect transistor. (d) Transfer characteristics (I_DS − V_GS) of FETs based on graphene exfoliated in one of the low k solvent. Width to length ratio (W/L) of the device was 3 and drain to source voltage (V_DS) was kept constant at 0.1 V.

The second observation is that number fraction of graphene layers can be directly controlled with the sonication time. As discussed earlier, by increasing t_s from 8 to 12 h, five-fold increase could be observed in number fraction of graphene monolayers. It suggests that overall yield can be increased not only by using appropriate organic solvents but also by optimizing the t_s. However, as we have discussed earlier in this article that increase in t_s results into cutting of graphene flakes, hence in order to get high production yield and large area of graphene layers, t_s should be optimized. In addition to surface energies, polarity of solvent is also playing an important role. Fig. 7 shows the Raman spectra of graphene monolayers exfoliated in low and high k solvents and the difference in the spectra is clearly visible. Graphene monolayers exfoliated in low k solvents (toluene and chlorobenzene) show diminutive D band (1350 cm⁻¹) whereas, in high k solvents (DMF and PC), prominent D band can be seen. It emphasizes the presence of disorders²⁰ in graphene layers exfoliated in low k solvents, is due to marginal functionalization and in high k is due to strong functionalization. This is also supported by DFT calculations which will be discussed later. Effect of the polarity of the solvents has been discussed in detail in our previous work.²¹

In spite of disorder in graphene's basal plane, we conclude that the effect of structural damage in functionalized graphene layers is quite low (I_D/I_G ∼ 0.4 and I_G/I_2D ∼ 0.5; where I_D, I_G and I_2D are intensities of Raman D, G and 2D peaks, respectively) as measured from Raman spectra. FT-IR spectroscopic measurements were also performed to understand the effect of high k solvents on structural changes in graphene monolayers. In addition to in plane C=C vibrations (∼1640 cm⁻¹), several other vibrations have also been observed for graphene exfoliated in DMF and PC (g-DMF and g-PC) indicating attachment of functional groups on graphene's basal plane. Vibrational signatures at 1093 cm⁻¹, 2900 cm⁻¹, 3300 cm⁻¹ (and 3800 cm⁻¹) in g-DMF and g-PC corresponds to C–O, C–H and O–H vibrations, respectively indicating the presence of solvent molecules in the proximity of graphene surface. We have also carried out electrical measurements on graphene based field effect transistors (FETs) which illustrates the superior quality of graphene monolayers. We have fabricated FETs based on graphene exfoliated in low and high k solvents. Fig. 7 also shows transfer characteristics of FET based on graphene exfoliated in toluene (g-toluene). Carrier mobility was found to be ∼10 000 cm² Vs⁻¹ with Dirac point at +1.0 V. These observations, corroborate that graphene exfoliated in low k solvent shows pristine behaviour whereas, in high k solvents there are defects in graphene's basal plane due to functionalization which causes shift²² in V_D, asymmetry²³ around V_D and reduction in carrier mobility²⁴ (see ESI†).

Density functional theory (DFT) has been used to understand, how graphene sheets are functionalized with different organic molecule during exfoliation process (Fig. 8).^25,26 Calculations were carried out using DFT with Lee–Yang–Parr correlation functional (B3LYP), with 631G-basis set. To find an energetically favorable structure of graphene with different organic molecules and the interaction strength between graphene and the organic molecules were estimated using DFT with graphene sheet having 150 carbon atoms. The adsorption energy is calculated by subtracting the adsorption energy of the separate systems containing isolated graphene sheets (E_GR) or isolated organic molecule (E_OM) from the adsorption energy of the combined relaxed system (E_GR–OM) and is defined as²⁵ E_b = E_GR–OM − (E_GR + E_OM). It is to be noted that the system (with negative adsorption energy) would be in thermodynamic equilibrium. In our case, for low k solvents (toluene and chlorobenzene), E_b comes out to be positive (∼0.071 eV) and for high k it is negative (∼−2.48 eV). It suggests that high k solvents (acetone, DMF and PC) can be easily adsorbed on graphene's basal plane whereas; low k solvents would not be in close proximity to graphene surface. It has also been noticed that the distance between solvent molecule and graphene surface is relatively high in case of low k solvents (∼4.34 A⁰) as compared to high k solvents (∼3.32 A⁰). Hence, high k solvents will introduce more perturbation as compared to low k solvents due to relatively close proximity to the graphene's basal plane. Re-aggregation of dispersed graphene flakes may be an important issue in LPE.²⁷

Fig. 8 Schematic representation for functionalization of graphene for the adsorption of (a) PC and (b) toluene onto graphene sheet (top and side views). From side view, it is visible that the distance of nearest atoms between graphene and organic molecule is larger for toluene than PC molecule. Color coding of atoms, grey atom: carbon atom of graphene, grey atom with red C: carbon atom of organic molecule, oxygen (red), hydrogen (white).

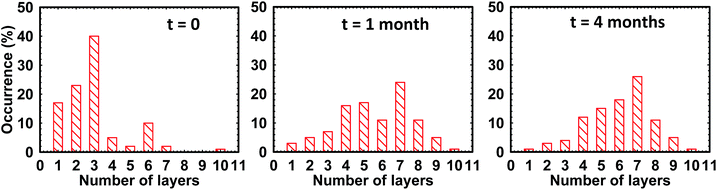
To check the stability against re-aggregation over longer time scale, variations in number fractions of graphene layers over a span of four months were monitored. We have carried out AFM measurement on several graphene flakes obtained from fresh and aged dispersions. Fig. 9 shows histograms representing the number fractions of graphene layers (exfoliated in toluene) over a time period of 4 months (aged dispersion). We have chosen toluene to check the stability of the dispersion because we get defect free graphene (negligible Raman D band) in toluene so its stability over longer time scale would be of special interest. For old dispersions (t = 1 month and t = 4 months), we see some aggregation of graphene flakes as compared to that of fresh dispersion (t = 0) as number fraction of monolayer graphene reduces from ∼20% (for fresh dispersions) to 2–3% in 4 months old dispersions. However, old dispersions contain individual graphene monolayers suggesting the stability of dispersions over a longer time period of 4 months.

Fig. 9 Histograms showing occurrence (number of visual observations) of graphene layers as a function of their respective layered structure, immediately after centrifugation (t = 0), one month after centrifugation (t = 1 month) and four months after centrifugation (t = 4 months) of toluene/HOPG based dispersions. (Data corresponds to 12 hour sonicated toluene/HOPG dispersion).

Conclusions

Here, we have demonstrated an efficient way to achieve high yield exfoliation of HOPG in various organic solvents to obtain excellent quality graphene monolayers. It has been shown that in addition to surface energies, polarity of solvents also plays crucial role in achieving high yield of graphene layers due to change in graphite surface chemistry assisted by functionalization. The marginal functionalization leads to weak p-type doping in low k and strong functionalization in high k solvents leads to n-type doping. It has also been shown that yield of graphene monolayers can also be controlled with sonication time. It has been observed that optimizing sonication time could lead us to achieve monolayer graphene size up to ∼35 microns which is at least one order of magnitude higher than previously reported values. Raman spectroscopic and electrical measurements indicate high quality of graphene monolayers. We have also checked the long term stability of the defect free graphene in solution phase and it was found that significant fraction of monolayers were present in the dispersion even after 4 months of centrifugation. It is anticipated that these findings would be of considerable interest in terms of its potential use in large-area applications,²⁸ from sensor^29,30 and device fabrication to liquid-phase chemistry.

Acknowledgements

We thank AIRF, JNU for providing TEM and IR facility. WITec GmbH is kindly acknowledged for providing help in Raman measurements. PKS and P. Y. thank CSIR and UGC, govt of India for financial support through fellowship.

Notes and references

1. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666.
3. K. S. Novoselov, Z. Jiang, Y. Zhang, S. V. Morozov, H. L. Stormer, U. Zeitler, J. C. Maan, G. S. Boebinger, P. Kim and A. K. Geim, Science, 2007, 315, 1379.
4. X. Du, I. Skachko, A. Barker and E. Y. Andrei, Nat. Nanotechnol., 2008, 3, 491.
5. C. Journet, W. K. Maser, P. Bernier and A. Loiseau, Nature, 1997, 388, 756.
6. S. M. Jung, H. Y. Jung, W. Fang, M. S. Dresselhaus and J. Kong, Nano Lett., 2014, 14, 1810.
7. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Nature, 2009, 457, 706.
8. W. Strupinski, K. Grodecki, A. Wysmolek, R. Stepniewski, T. Szkopek, P. E. Gaskell, A. Gruneis, D. Habrer, R. Bozek, J. Krupka and J. M. Baranowski, Nano Lett., 2011, 11, 1786.
9. W. Norimatsu and M. Kusunoki, Phys. Chem. Chem. Phys., 2014, 16, 3501.
10. S. Park and R. S. Ruoff, Nat. Nanotechnol., 2009, 4, 217.
11. W. Zhao, M. Fang, F. Wu, H. Wu, L. Wang and G. Chen, J. Mater. Chem., 2010, 20, 5817.
12. B. Ankamwar and F. Surti, Chem. Sci. Trans., 2012, 1, 500.
13. K. N. Kudin, B. Ozbas, H. C. Schniepp, R. K. Prud, I. A. Aksay and R. Car, Nano Lett., 2008, 8, 36.
14. X. Díez-Betriu, S. Álvarez-García, C. Botas, P. Álvarez, J. Sánchez-Marcos, C. Prieto, R. Menéndez and A. de Andrés, J. Mater. Chem. C, 2013, 1, 6905.
15. Y. Hernandez, V. Nicolosi, M. Lotya, F. M. Blighe, Z. Sun, S. De, I. T. McGovern, B. Holland, M. Byrne, Y. K. Gun'Ko, J. J. Boland, P. Niraj, G. Duesberg, S. Krishnamurthy, R. Goodhue, J. Hutchison, V. Scardaci, A. C. Ferrari and J. N. Coleman, Nat. Nanotechnol., 2008, 3, 563.
16. M. Lotya, Y. Hernandez, P. J. King, R. J. Smith, V. Nicolosi, L. S. Karlsson, F. M. Blighe, S. De, Z. Wang, I. T. McGovern, G. S. Duesberg and J. N. Coleman, J. Am. Chem. Soc., 2009, 131, 3611.
17. J. C. Meyer, A. K. Geim, M. I. Katsnelson, K. S. Novoselov, T. J. Booth and S. Roth, Nature, 2007, 446, 60.
18. S. C. Roh, E. Y. Choi, Y. S. Choi and C. K. Kim, Polymer, 2014, 55, 1527.
19. D. Y. Ryu, K. Shin, E. Drockenmuller, C. J. Hawker and T. P. Russell, Science, 2005, 308, 236.
20. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401.
21. P. Kumar Srivastava and S. Ghosh, Appl. Phys. Lett., 2013, 102, 043102.
22. B. Guo, Q. Liu, E. Chen, H. Zhu, L. Fang and J. R. Gong, Nano Lett., 2010, 10, 4975.
23. D. S. Novikov, Appl. Phys. Lett., 2007, 91, 102102.
24. Z. H. Ni, L. A. Ponomarenko, R. R. Nair, R. Yang, S. Anissimova, I. V. Grigorieva, F. Schedin, P. Blake, Z. X. Shen, E. H. Hill, K. S. Novoselov and A. K. Geim, Nano Lett., 2010, 10, 3868.
25. L. Jing, P. Huang, H. Zhu and X. Gao, Small, 2013, 9, 306.
26. M. Chi and Y. P. Zhao, Comput. Mater. Sci., 2012, 56, 79.
27. C. Shih, S. Lin, M. S. Strano and D. Blankschtein, J. Am. Chem. Soc., 2010, 132, 14638.
28. X. Li, Y. Zhu, W. Cai, M. Borysiak, B. Han, D. Chen, R. D. Piner, L. Colombo and R. S. Ruoff, Nano Lett., 2009, 9, 4359.
29. F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Nat. Mater., 2007, 6, 652.
30. S. Borini, R. White, D. Wei, M. Astley, S. Haque, E. Spigone and N. Harris, ACS Nano, 2013, 7, 11166.

---

Footnote

† Electronic supplementary information (ESI) available: Method to calculate yield of graphene monolayers, associated chart and a brief discussion on electronic structure calculations. See DOI: 10.1039/c5ra12464f

---