Mechanical properties and structure of solvent processed novolac resin/layered silicate: development of interphase region
Abstract
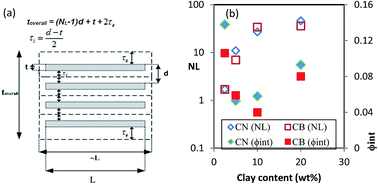
Composites of phenol-formaldehyde (PF) resin with Closite Na+ and Closite 30B up to 20 wt% loadings were prepared by solution mixing. Tensile testing showed that both pristine and organically modified clays increased considerably the mechanical properties of PF resin at 2.5 wt% loading followed by marginal improvement or even sacrificed properties at high loadings. DMA and DSC analyses suggested development of a highly crosslinked and well adhered interphase around silicate layers. A novel three-phase model considering the interphase region was proposed to predict composite modulus. The model was successfully employed to correlate morphological characteristics and mechanical properties of PF/clay composites.

 Please wait while we load your content...
Please wait while we load your content...