Size dependent electronic band structures of β- and γ-graphyne nanotubes

Abstract

In the present paper, density functional theory calculations have been implemented by using Dmol³ to study the electronic band structures of β-graphyne nanotubes (βGyNTs) and γ-graphyne nanotubes (γGyNTs). Our results found different GyNTs show diverse electronic band structures. All βGyNTs have quite small band gaps without any correlation with tube size. Meanwhile, γGyNTs, no matter zigzag or armchair, exhibit semiconductor characteristics with oscillatory band gap ranging from 0.48 eV to 1.20 eV. Furthermore, based on the variation of band gap, both zigzag and armchair γGyNTs can be divided into two subgroups: 2m and 2m + 1 where n is a positive integer, following the order of 2m + 1 > 2m.

---

Introduction

During the last two decades, carbon-based materials including fullerenes,^1,2 carbon nanotubes (CNTs)^3,4 and graphene,⁵ have received enormous amounts of attention from theorists and experimentalists. Especially, CNTs constituted by only sp²-like carbons could be either metallic or semiconducting, and they have been intensively exploited in electronic devices.^6,7 Recently a new carbon allotrope by inserting acetylenic linkage (–C≡C–) into graphene, named graphyne, has been receiving growing attention. The coexistence of sp and sp² carbons grants graphyne outstanding characteristics.^8–12 These unique properties could allow graphyne to have some potential applications.^13–15 The presence of acetylenic linkages allows graphyne to exist in several different two-dimensional structures, such as α-, β-, and γ-graphyne.^9–11 Since CNTs can be considered as seamless cylinders of graphene sheets, we can also build graphyne nanotubes (GyNTs) via the same approach. Recently, graphdiyne nanotubes (GDyNTs) has been successfully synthesized and exhibited high-performance field emission properties,¹⁶ which gives a possibility for realization of single-walled graphyne nanotubes (GyNTs).

Comparing with CNTs, GyNTs have not received much attention though it deserved.^17,18 Computational studies have been carried out to investigate the electronic band structure via tight-binding (TB) method.^19,20 However, there are two very import parameters ignored in TB method, σ–π hybridization effect²¹ and the coexistence of sp and sp² hybridized carbon. Such a weakness of TB has been exposed by recent studies on CNTs. Theoretical and experimental approaches have proved that zigzag (n, 0) CNTs are typical semiconductor when n ≠ 3m,^22,23 while zigzag (n, 0) CNTs when n = 3m were predicted to be metallic via the TB method.^24,25 Afterwards, recent research based on DFT calculations disclosed a small energy band gap,^26,27 which has been experimentally confirmed.²⁸ The (n, 0) SWCNTs with n = 3m showed semiconductor property with band gap of 0.080 ± 0.005 eV for (9, 0), 0.042 ± 0.004 eV for (12, 0) and 0.029 ± 0.004 eV for (15, 0) SWCNT. As such different electronic band structure of αGyNTs by TB method compared with our calculations based on density functional theory (DFT) was revealed.²⁹ To our knowledge, DFT calculations have not been systematically implemented for β-graphyne nanotubes (βGyNTs) and γ-graphyne nanotubes (γGyNTs), which motivates us to undertake the present study. From the calculated electronic band structure, we found that βGyNTs and γGyNTs possess different electronic structures from ordinary CNTs and αGyNTs. βGyNTs have small band gaps without correlation with tube size, while γGyNTs are typical semiconductor but with different oscillatory band gap behavior compared to the CNTs.

Computational method

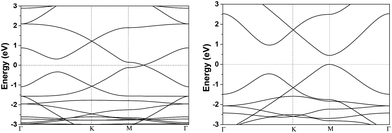
In this study, DFT-D calculations were carried out by DMol³ module³⁰ in Material Studio 5.5. In earlier paper, different DFT method including PWC functional³¹ belonging to LDA, PW91,³¹ BLYP³² and PBE functionals^33,34 belonging to GGA, were implemented to investigate the band structures of αGyNTs and gave nearly the same results. Thus, in the present paper PBE method was utilized with the consideration of dispersive interaction correction (PBE-D). Such PBE-D method has been intensively applied to study carbon related materials.^35,36 Moreover, there is no spin restriction imposed during calculations. For all calculations, 20 Å vacuum space was imposed to avoid interlayer interactions. All electron treatment was performed and a double numerical plus polarization (DNP) basis set was used. The convergence tolerance of energy was 10⁻⁵ hartree, and the maximum allowed force and displacement were 0.002 hartree per Å and 0.005 Å, respectively. The unit cell of β- and γ-graphyne was fully optimized with 2D hexagonal symmetry with k-point meshes of 7 × 7 × 1, and the lattice constant (a) was computed to be 9.527 and 6.923 Å, respectively. As noted in Fig. 1, the band structure of β-graphyne has a zero band gap, while that of γ-graphyne has a band gap (E_g) of 0.47 eV at M high symmetric point. Dispersive interactions are important in electronic structure calculations of carbon materials such as graphene.³⁷ Herein we compared the E_g obtained with and without dispersion correction. The E_g without dispersion correction was reported to be 0.42 eV,²⁰ which was further verified by our result of 0.43 eV by merely PBE method. Since pure DFT often underestimates band gap, dispersion correction could relieve such a problem.

Fig. 1 Band structures of 2D β-graphyne (left) and γ-graphyne (right).

Based on the optimal unit cell of β- and γ-graphyne, the corresponding zigzag and armchair nanotubes were built by rolling up film along different orientation. The structure of each nanotube was first fully optimized with Brillouin zone k-point meshes of 1 × 1 × 4. Then the k-point meshes was increased to 2 × 2 × 50, which should be large enough to obtain reliable electronic band structure (50 is the maximum value allowed by Dmol³). For each tube, the cohesive energy (E_coh) was calculated as follows:

E_coh = E_total/N_C − E_C

where E_total, N_C and E_C stand for the total energy, number of carbon atoms and energy of isolated carbon atom, respectively. More negative E_coh implies energetically more stable structure.

Results and discussion

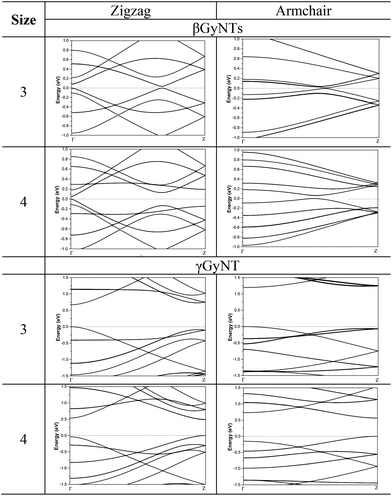
As we did in earlier study,²⁹ the chirality of tubes was characterized by applying nomenclature (n, m). As shown in Fig. 2, the chirality of βGyNTs and γGyNTs is slightly different from that of αGyNTs possessing hexagonal carbon ring. To maintain consistency with αGyNTs, zigzag and armchair were still used to name the chirality of βGyNTs and γGyNTs. Following such notation, (n, 0) and (n, n) stand for zigzag and armchair nanotubes, respectively. These tubes were denoted by N_z-Z-β (γ) GyNTs and N_a-A-β (γ) GyNTs, where N_z and N_a represent the tube size of zigzag and armchair nanotubes, respectively. Fig. 2 shows the optimized structures of βGyNTs and γGyNTs with N_z and N_a being 4 for instance. The relationship between cohesive energy (E_coh) and tube size (N_z or N_a) was pictured in Fig. 3. The cohesive energy for βGyNTs and γGyNTs monotonically decreased as the tube size increases implying gradual reduction in surface strain. For both βGyNTs and γGyNTs, the cohesive energy of armchair was always smaller than that of zigzag when N_z = N_a because A-GyNTs has larger diameter. The cohesive energy of βGyNTs and γGyNTs gradually converged to −7.11 and −7.32 eV per atom since surface strain tends to decrease. Those values are larger than that of αGyNTs with −7.02 eV per atom. Such values are comparable to that of fullerene with −7.29 eV per atom³⁸ that makes the single walled GyNT to be realized in near future.

Fig. 2 Optimized structures of (4, 0)- and (4, 4)-βGyNT and γGyNT.

Fig. 3 Cohesive energy vs. tube size of zigzag and armchair graphyne nanotubes.

Then the corresponding electronic band structure of βGyNT with N_z = 3 and 4 were plotted in Fig. 4. For 3-Z-βGyNT, one can see that the valence band maximum (VBM) reaches to the Fermi level (E_F) and the conduction band minimum (CBM) locates above E_F, inducing a direct band gap (E_g) of 0.03 eV between Γ and Z point. Meanwhile, the location of such direct band gap moves to the top of Γ point for 4-Z-βGyNT whose E_g was 0.05 eV. Further analysis confirmed the dependence of band gap's location upon the parity of N_z. To elucidate the size dependence of band gap, the variation of E_g as a function of N_z was shown in Fig. 5 and no correlation between E_g and tube size was found for Z-βGyNTs.

Fig. 4 The band structures of βGyNT and γGyNT for N_z/N_a = 3 and 4.

Fig. 5 The variation of β and γGyNTs' band gaps as a function of tube size.

The band structure of Z-βGyNTs is distinctly diverse from zigzag CNTs and αGyNTs. It was determined that zigzag (n, 0) CNTs are semiconductor and show an oscillatory band gap dependence on tube size (n). The band gap follows the rank order: 3m − 1 > 3m + 1 > 3m.^22,23,28 Recently, we carried out reliable DFT calculations to investigate the electronic structures of αGyNTs and found Z-αGyNTs possess qualitatively similar band gap behavior.²⁹ All Z-αGyNTs are semiconductors and exhibit strong dependence on tube size. N_z-Z-αGyNTs can be classified into three families according to band gap variation: N_z = 3m − 1, 3m, and 3m + 1 resulting in the following rank order of band gap magnitudes: 3m − 1 > 3m + 1 > 3m.

For the band structure of A-βGyNTs, as displayed in Fig. 4, the VBM reaches to E_F, and the CBM locates above E_F, inducing a direct band gap between Γ and Z point. The E_g of A-βGyNTs was calculated to be about 0.01 eV except for the cases of N_z = 4 and 9. The E_g of 4- and 9-A-βGyNT were 0.06 eV and 0.11 eV, respectively. Considering DFT usually underestimates band gap, A-βGyNTs could be concluded as semiconductor. Similar to Z-βGyNTs, A-βGyNTs do not show a size dependence of band gap as noted in Fig. 5 and have different electronic band structure compared to armchair CNTs and A-αGyNTs. Armchair CNTs had been experimentally determined to be metallic.^28,39 Furthermore, A-αGyNTs were concluded to be semiconductors when tube size is small and showed downward trend on tube size, then becomes metallic as the tube size increases.

The band structure of γGyNTs showed that the VBM reaches to E_F and the CBM locates above E_F, thus resulting in direct band gaps. Similar to Z-βGyNTs, the band gap location of γGyNTs was found to be related with the parity of tube size. When N_z or N_a was odd, the direct band gap located at Γ point, while that of even N_z or N_a located at Z point. Furthermore, all γGyNTs were semiconductors with moderate E_g ranging from 0.48 eV to 1.20 eV as pictured in Fig. 5. Moreover, it was further revealed that the band gap of Z-γGyNTs exhibited oscillatory and size dependent behavior, which is similar to zigzag CNTs and αGyNTs. However, differently from zigzag CNTs and αGyNTs, Z-γGyNTs could be classified into two families with N_z = 2m and 2m + 1 (n is a positive integer) following the order of band gap magnitudes: 2m + 1 > 2m according to band gap variation. Additionally, armchair CNTs, αGyNTs and βGyNTs are either semiconductor with very small band gap or metal, while A-γGyNTs are typical semiconductor with moderate band gaps. Similar to Z-γGyNTs, A-γGyNTs can also be divided into two subgroups with N_a = 2m and 2m + 1 following the order of band gap magnitudes: 2m + 1 > 2m. The oscillatory behavior of the band gap of γGyNTs was also observed from DFTB study.¹⁷ But one point should be emphasized that the band gap of A-γGyNTs in present paper is always larger than that of Z-γGyNTs when N_a = N_z, while it is overturned by DFTB method.¹⁷ Such disharmony may originate from the inadequacy of tight-binding-link treatment in DFTB method. It would be elusive until more expensive calculations like GW method⁴⁰ or experiments report the band gaps of γGyNTs in the future. In addition, the band gaps of both Z-γGyNTs and A-γGyNTs gradually decreased as tube size increased, and were predicted to converge to that value of γ-graphyne film.

Conclusions

Our DFT calculation showed different GyNTs have diverse electronic band structures. αGyNTs possess qualitatively similar band gap behaviour to ordinary CNTs. Z-αGyNTs were disclosed as semiconductors with band gap which is strongly dependent on tube size. N_z-Z-αGyNTs can be classified into three families: N_z = 3m − 1, 3m, and 3m + 1 resulting in the following rank order of band gap magnitudes: 3m − 1 > 3m + 1 > 3m. Meanwhile, A-αGyNTs are semiconductors with small tube size then becomes metallic as the tube size increases.²⁹ However, βGyNTs appeared to be atypical among CNTs and GyNTs. All βGyNTs have quite small band gaps but without any correlation with tube size. For γGyNTs, no matter zigzag or armchair, semiconductor character was clearly observed with moderate band gap of 0.48–1.20 eV. Both Z- and A-γGyNTs can be divided into two subgroups: 2m and 2m + 1 where n is positive integer, following the order of band gap magnitudes: 2n +1 > 2n. Their band gaps decreased as tube size increases, and were predicted to converge to the value of 2D γ-graphyne. Moreover, the band gap of A-γGyNTs is always larger than that of Z-γGyNTs. According to the electronic properties, γGyNTs would be a potential candidate as semiconductors with controllable band gap by tuning the tube size.

Acknowledgements

This work was supported by National Research Foundation (NRF) grants funded by the Korean government (MEST) (2007-0056343). We acknowledge the financial support from the Ministry of Education, Science and Technology, subjected to the project EDISON (Education-research Integration through Simulation On the Net, Grant No.: 2012M3C1A6035359).

Notes and references

1. D. M. Guldi, B. M. Illescas, C. M. Atienza, M. Wielopolskia and N. Martin, Chem. Soc. Rev., 2009, 38, 1587–1597.
2. T. Braun, A. P. Schubert and R. N. Kostoff, Chem. Rev., 2000, 100, 23–27.
3. C. Wang, K. Takei, T. Takahashi and A. Javey, Chem. Soc. Rev., 2013, 42, 2592–2609.
4. P. M. Ajayan, Chem. Rev., 1999, 99, 1787–1799.
5. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J. H. Ahn, P. Kim, J. Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710.
6. M. S. Dresselhaus, G. Dresselhaus, J. C. Charlier and E. Hernandez, Philos. Trans. R. Soc., A, 2004, 362, 2065–2098.
7. M. F. L. de Volder, S. H. Tawfick, R. H. Baughman and A. J. Hart, Science, 2013, 339, 535–539.
8. Y. Li, L. Xu, H. Liu and Y. Li, Chem. Soc. Rev., 2014, 43, 2572–2586.
9. J. Kang, J. Li, F. Wu, S. S. Li and J. B. Xia, J. Phys. Chem. C, 2011, 115, 20466–20470.
10. S. W. Cranford and M. J. Buehler, Carbon, 2011, 49, 4111–4121.
11. Y. Y. Zhang, Q. X. Pei and C. M. Wang, Appl. Phys. Lett., 2012, 101, 081909.
12. B. Kang, H. Liu and J. Y. Lee, Phys. Chem. Chem. Phys., 2014, 16, 974–980.
13. H. Zhang, M. Zhao, X. He, Z. Wang, X. Zhang and X. Liu, J. Phys. Chem. C, 2011, 115, 8845–8850.
14. C. Li, J. Li, F. Wu, S. S. Li, J. B. Xia and L. W. Wang, J. Phys. Chem. C, 2011, 115, 23221–23225.
15. B. Kang and J. Y. Lee, J. Phys. Chem. C, 2014, 118, 12035–12040.
16. G. X. Li, Y. L. Li, X. M. Qian, H. B. Liu, H. W. Lin, N. Chen and Y. J. Li, J. Phys. Chem. C, 2011, 115, 2611–2615.
17. X. M. Wang and S. S. Lu, J. Phys. Chem. C, 2013, 117, 19740–19745.
18. Y. S. Wang, P. F. Yuan, M. Li, W. F. Jiang, Q. Sun and Y. Jia, J. Solid State Chem., 2013, 197, 323–328.
19. V. R. Coluci, S. F. Braga, S. B. Legoas, D. S. Galvao and R. H. Baughman, Phys. Rev. B, 2003, 68, 035430.
20. V. R. Coluci, S. F. Braga, S. B. Legoas, D. S. Galvao and R. H. Baughman, Nanotechnology, 2004, 15, S142–S149.
21. X. Blase, L. X. Benedict, E. L. Shirley and S. G. Louie, Phys. Rev. Lett., 1994, 72, 1878–1881.
22. H. W. Wang, B. C. Wang, W. H. Chen and M. Hayashi, J. Phys. Chem. A, 2008, 112, 1783–1790.
23. R. B. Weisman and S. M. Bachilo, Nano Lett., 2003, 3, 1235–1238.
24. J. W. Mintmire, B. I. Dunlap and C. T. White, Phys. Rev. Lett., 1992, 68, 631–634.
25. R. Saito, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 1804–1811.
26. Y. Matsuda, J. Tahir-Kheli and W. A. Goddard, J. Phys. Chem. Lett., 2010, 1, 2946–2950.
27. T. Ito, K. Nishidate, M. Baba and M. Hasegawa, Surf. Sci., 2002, 514, 222–226.
28. M. Ouyang, J. L. Huang, C. L. Cheung and C. M. Lieber, Science, 2001, 292, 702–705.
29. B. Kang and J. Y. Lee, Carbon, 2015, 84, 246–253.
30. B. Delley, J. Chem. Phys., 2000, 113, 7756–7764.
31. J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244–13249.
32. A. D. Becke, J. Chem. Phys., 1988, 88, 2547–2553.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
34. J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539.
35. J. Ma, A. Michaelides, D. Alfe, L. Schimka, G. Kresse and E. G. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 033402.
36. W. M. Sun, Y. X. Bu and Y. X. Wang, J. Phys. Chem. C, 2011, 115, 3220–3228.
37. M. Alonso, T. Woller, F. J. Martin-Martinez, J. Contreras-Garcia, P. Geerlings and F. De Proft, Chem.–Eur. J., 2014, 20, 4931–4941.
38. X. Hua, T. Cagin, J. Che and W. A. Goddard, Nanotechnology, 2000, 11, 85–88.
39. J. W. G. Wildoer, L. C. Venema, A. G. Rinzler, R. E. Smalley and C. Dekker, Nature, 1998, 391, 59–62.
40. G. Onida, L. Reining and A. Rubio, Rev. Mod. Phys., 2002, 74, 601–659.

---