Monte Carlo study of the micelles constructed by ABCA tetrablock copolymers and their formation in A-selective solvents

Abstract

The phase behavior of the ABCA tetrablock copolymers in A-selective solvents is investigated using Lattice Monte Carlo simulation. The main focus is the effects of the solvophobic interactions of blocks B and C (ε_BS and ε_CS) on the micelle morphologies. Three kinds of ABCA tetrablock copolymers, i.e., A₂B₆C₆A₂, A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers, are considered. Phase diagrams of these three tetrablock copolymers as a function of ε_CS and the solvophobic interaction difference between blocks B and C (which is measured by r = ε_BS/ε_CS) are given and discussed. It is found that r and ε_CS can both affect the specific surface area of micelles and lead to the morphological changes of ABCA tetrablock copolymer micelles. In addition, r can change the solvophobic chain conformation and hence affect the micro-structures of the solvophobic parts of the micelles. For A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers, several novel micelle morphologies, such as the bended Janus ribbon and lamella, short Janus tube, and bowl-shaped semivesicle, are obtained. Interestingly, it is found that in the phase diagrams of A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers, the micelle type with Janus-like solvophobic parts is the majority micelle type, which mainly results from the solvophobic interaction balance between blocks B and C. Moreover, the formation pathways for these novel Janus-type micelles are given and discussed.

---

1. Introduction

Block copolymers have attracted much attention due to their ability to self-assemble into nanostructures with well-defined morphologies in selective solvents. By tuning the chemical structure of the monomers, the degree of polymerization, and the solvent properties, a series of micelles, such as spherical micelle, cylindrical micelle, lamella, and vesicle, can be obtained in selective solvents.^1–4 In general, the solvophobic parts of the micelles formed by AB diblock (or ABA triblock) copolymers only contain one kind of blocks. However, if another solvophobic block C is introduced, the solvophobic part of micelle will be composed of two components, and it can be separated into multiple nanoscale domains due to the incompatibility between different solvophobic components. This kind of micelle with multiple solvophobic parts is defined as “multicompartment micelle”. Multicompartment micelle is quite similar to some biological substances which also have subdivided domains with different physical and chemical properties, therefore, it can be used to mimic biological structures and features.^5–7 On the other hand, multicompartment micelles are considered to have potential applications on drug delivery due to their ability for carrying two or more agents simultaneously within different compartments in one micelle.^8–10 Hence, plenty of researches have been focused on the preparation of multicompartment micelles.

ABC triblock copolymer with two sequential solvophobic blocks B and C is an ideal candidate for the preparation of multicompartment micelles.^11–20 Using such triblock copolymers, Yu and Eisenberg¹¹ obtained “onion-like” spherical micelles in which different solvophobic blocks are separated into concentric shells. Later, Ma et al.¹² observed similar “onion-like” spherical micelles. However, via adjusting the volume fractions and the solvophobic interaction of blocks B and C in ABC triblock copolymers, the “onion-like” spherical micelles changed into the spherical micelles with novel bump-surface. Afterwards, a phase diagram of such bump-surface multicompartment micelles formed by ABC triblock copolymers was provided by Kong et al.¹³ using Monte Carlo simulation. In addition, double helix cylindrical micelles have been obtained by Dupont et al.¹⁴ in experiments by tuning the content of selective solvents. Recently, Müller and co-workers^15,16 presented a novel and versatile way to precisely predict morphological structures of multicompartment micelles self-assembled from ABC triblock copolymers. Using a directed step-wise self-assembly via pre-assembled subunits and sequential reductions of the freedom degrees of different blocks, they obtained thermodynamically labile morphologies of multicompartment micelles with extremely homogeneous structure. On the other hand, ABC miktoarm star terpolymer is another kind of terpolymer that can be used for preparing multicompartment micelles, and has been widely investigated.^21–27 Lodge and co-workers^21–26 reported a series of novel multicompartment micelles formed by [poly(ethylethylene)]-[poly(ethylene oxide)]-[poly(perfluoropropylene oxide)] (termed μ-EOF) miktoarm star terpolymers including laterally nanostructured vesicles and bowl-shaped semivesicles, polygonal-shaped bilayer sheets and so on. Soon after, Kong et al.²⁷ investigated similar star terpolymers using Monte Carlo simulation. More multicompartment micelles were predicted in their simulations, and the simulation results indicated that tuning the solvent quality or the incompatibility between the two solvophobic arms can induce morphological transitions.

Due to the rapid developments in technology for synthetic polymer chemistry, the synthesis of well-defined block copolymers with fine controlled composition and block sequence, such as ABCA tetrablock copolymers, becomes more feasible.^28,29 In recent years, the ABCA tetrablock copolymers have attracted much attention. The molecular configuration of the ABCA tetrablock copolymers is quite similar to that of the ABC triblock copolymers aforementioned. However, a small change in the molecular configuration from ABC- to ABCA-type can lead to a significant change in the micro-phase separated structure of the micelles. Gomez et al.³⁰ once synthesized an ABCA tetrablock copolymer which can form locally planar aggregates. Due to the incompatibility between the middle blocks B and C, these two blocks are totally phase separated into different sides of the aggregates and then forming Janus-type microstructures in the aggregates. Brannan and Bates³¹ reported a type of vesicles formed by poly(ethylene oxide)-b-poly(styrene)-b-poly(butadiene)-b-poly(ethylene oxide) (PEO-PS-PB-PEO) tetrablock copolymer with a microphase segregated solvophobic core. They found that increasing the PEO block size would induce the transition of the solvophobic core structure from an asymmetric bilayer with the PB and PS blocks respectively forming inner and outer solvophobic surfaces, to the layer in which the PB and PS blocks exhibiting either a bicontinuous or a hexagonally arranged order. It is noteworthy that the Janus-type solvophobic core of the planar micelles and the asymmetric bilayer in the vesicles formed by ABCA-type tetrablock copolymers cannot be formed by ABC triblock copolymers with two sequential solvophobic blocks B and C. The introduction of solvophilic blocks A at both ends of the ABCA chains has a significant influence on the micelle type finally formed. Thereafter, similar ABCA tetrablock copolymer systems were studied by Cui and Jiang³² using Monte Carlo simulation. Their simulation results indicated that the block length ratio and the solvophobic interaction of blocks B and C are key factors determining the solvophobic layer structure of the vesicles. Most recently, Greenall and Marques³³ using self-consistent field theory designed ABCA tetrablock copolymers which can form asymmetric vesicles with a preferred curvature and illustrated how to control ABCA tetrablock copolymer vesicle size.

From the aforementioned investigations, it can be found that previous works about the self-assemblies of ABCA tetrablock copolymers are limited within the scope of multicompartment vesicles. Other multicompartment micelle morphologies that might be obtained from ABCA tetrablock copolymers are hardly concerned. Therefore, systematic Monte Carlo simulation is performed in the current paper to investigate the multicompartment micelles formed by ABCA tetrablock copolymers with two incompatible solvophobic blocks B and C in selective solvents. According to the previous studies of ABC triblock^12–14 or miktoarm terpolymer,^21,23,27 two factors (i.e., the selective solvent property and the block length ratio of different solvophobic blocks) are found to play an important role in the self-assembly behavior of block copolymer. Hence, the focus of the current paper is the effects of these two factors on the phase behavior of ABCA tetrablock copolymers. In this paper, several novel micelle structures, e.g., bended Janus ribbon (or lamella), short Janus tube, and bowl-shaped semivesicles with multicompartment solvophobic layer, are obtained. The formation conditions, as well as the formation mechanisms of these novel structures are discussed and elucidated in details.

2. Model and method

2.1. Lattice model of block copolymer chains in Monte Carlo simulation

The dynamic Lattice Monte Carlo simulation method is used in this study. The coarse-grained single-site bond fluctuation model proposed by Carmesin and Kremer³⁴ and by Larson^35,36 was employed to represent lattice block copolymer chains. This model has been widely used for modeling the microphase separation of block copolymers in solution.^{12,13,27,32,39,41} In this paper, the simulation of self-avoiding chains was carried out in a simple cubic simulation box of volume V = L × L × L with L = 50. Periodic boundary conditions are imposed in all three directions. The permitted bond length of block copolymer chains is 1 and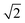 according to the single-site bond fluctuation model. Thus, each lattice site has 18 nearest neighbor sites in a 3 dimensional space. In the simulation box, each lattice site was occupied by either a monomer of the block copolymers or a solvent, and two monomers cannot occupy the same lattice site simultaneously.

There are many kinds of sampling methods to achieve the evolution of chain configurations in Monte Carlo simulation, such as the configurational-bias method,^37,38 which makes it possible to carry out large scale conformational changes of polymer chains in a single trial move, and the microrelaxation model, which is highly efficient in relaxing local chain conformation on the lattice.^39–41 In this paper, the configuration evolution of the polymer chains is achieved through local monomer move using the microrelaxation model. The microrelaxation model is defined as follows: a monomer is randomly chosen to exchange with one of its 18 nearest neighbors. If the neighbor is a solvent molecule, then exchange with the bead is attempted. If the exchange does not violate the bond length restriction, the exchange is allowed. This process constitutes a single movement. If the exchange would break two chain connections, it is disallowed. If the exchange creates a single break in the chain, the solvent molecule will continue to exchange with subsequent monomers along the chain until reconnection of the links occurs. The acceptance or rejection of the attempted move is further governed by the Metropolis rule:⁴² if the energy change ΔE is negative, the exchange is accepted. Otherwise, the exchange is accepted with a probability of P = exp[−ΔE/(k_BT)], where 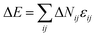is the energy change caused by the attempted move; ΔN_ij is the number difference of the nearest neighbor pairs between components i and j before and after the movement, where i, j = A, B, C, and S (solvent), respectively; ε_ij is the reduced interaction intensity between i and j; and k_B is the Boltzmann constant and assumed to be 1 in the whole simulation. The parameter T is the temperature.

The annealing method for obtaining stable micelle structures was implemented in the current paper, that is, the inverse temperature 1/T was changed gradually from 0 (representing the athermal state of T = ∞) to a given positive value with 1/T = 0.1 (representing a lower temperature). The annealing process was achieved by 400 annealing steps. In other words, the annealing rate (i.e., the increasing rate of 1/T) was set as 0.00025 per annealing step. At each annealing step, 7000 Monte Carlo Steps (MCS) were performed. In one MCS, on the average, each monomer has attempted one exchange move. It is noteworthy that the annealing speed adopted in this paper is rather slow (corresponding to the situation in which selective solvents are dropwise added into solutions in experiments), which is thought to be suitable for obtaining stable states in dilute solution in Monte Carlo simulation.⁴³ After 400 annealing steps, keeping 1/T = 0.1 unchanged, another 200 annealing steps were carried out to confirm that the final structures are in stable state.

2.2. The settings of the parameters

In this paper, the studied tetrablock copolymer is denoted as A_n1B_n2C_n3A_n1. Each copolymer chain contains N monomers, and N = n₁ + n₂ + n₃ + n₁ = 16 which is kept unchanged. The simulation box is filled with tetrablock copolymers and solvents. The volume fraction of polymers (C_P) in the simulation box is an important factor for obtaining complex micelles according to the Monte Carlo study reported by Kong et al.⁴⁴ Their study showed that the micelle morphologies formed by ABA triblock copolymers in selective solvents are richer and more complex in the systems with relatively higher C_P (C_P ranges from 0.03 to 0.07 in their study). Therefore, the value C_P = 0.07 has been chosen in the current paper, and the number of polymer chains N_chains ≈ 547 is calculated from N_chains = V × C_P/N consequently.

The A_n1B_n2C_n3A_n1 tetrablock copolymer studied in the current paper consists of two short solvophilic blocks A (i.e., n₁ = 2) and two solvophobic blocks B and C (i.e., n₂ + n₃ = 12). The ratio of the solvophilic block length to the solvophobic block length can be calculated as 2n₁ : (n₂ + n₃) = 1 : 3. The reason for choosing such ratio is that the amphiphilic block copolymers with relatively shorter solvophilic blocks tend to form crew-cut micelles,⁴⁵ which is the main micelle type considered in this paper. Another reason for choosing such ratio is that we want to simulate the ABCA tetrablock copolymer which is similar to the PEO-PB-PS-PEO tetrablock copolymers used by Brannan and Bates.³¹ In their experiments, the PEO-PB-PS-PEO tetrablock copolymers with relatively short PEO blocks can form the asymmetric vesicles with PS and PB blocks located at the outer and inner surface, respectively. The length of PEO blocks is the main factor that they changed. However, in the current paper, the solvophilic block length is kept unchanged, and the solvophobic parts are changed from B₆C₆ to B₈C₄ to investigate the block length ratio of different solvophobic blocks on the microstructures of various multicompartment micelles formed by ABCA tetrablock copolymers.

In order to mimic the amphiphilic nature of the ABCA tetrablock copolymers in A-selective solvents, the interaction parameter ε_AS was set as −1 to make the solvophilic blocks A stretch into the solution, and make the micelles stable. The interaction parameters ε_BS and ε_CS are set as positive to measure the solvophobic interaction of blocks B and C, respectively. In this paper, ε_BS and ε_CS are variable to elucidate the effect of solvophobic interactions on the phase behavior of ABCA tetrablock copolymers. ε_CS ranges from 2.0 to 3.5, and ε_BS = rε_CS, where r is the ratio of ε_BS to ε_CS, and r ranges from 0.25 to 1.0, indicating that the solvophobic interaction of block B is always lower than or equal to the solvophobic interaction of block C. The parameters ε_AB and ε_AC were set as ε_AB = ε_AC = 1 to mimic the incompatibilities between solvophilic block and solvophobic blocks. Note that stronger repulsive interaction between blocks B and C, that is ε_BC = 2, is needed to ensure that the two solvophobic blocks can phase separated into different compartments. In addition, all other self-interaction parameters between the same components (i.e., ε_AA, ε_BB, ε_CC and ε_SS) were set as 0.

From the aforementioned parameter settings, it can be found that there are three varied parameters concerned in this paper, which are the solvophobic interactions of block C (ε_CS, which is varied from 2.0 to 3.5), the solvophobic interaction difference between blocks B and C (which is measured by r = ε_BS/ε_CS, and r is varied from 0.25 to 1.0), and the chain length ratio of blocks B to C (which is varied from 6 : 6 to 8 : 4). From the selected values of these three parameters, it can be seen that the solvophobic interaction of block B (ε_BS) is always smaller than that of block C (ε_CS), while the chain length of block B is always longer than block C in most cases. Therefore, the purpose of this paper is to find out the self-assembly behaviors of the ABCA tetrablock copolymers in which the longer solvophobic block (B) has weaker solvophobicity, while the shorter solvophobic block (C) has stronger solvophobicity.

3. Results and discussion

In this section, three kinds of ABCA tetrablock copolymers are employed: A₂B₆C₆A₂ tetrablock copolymer in which the solvophobic block length of B and C is equal; A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers in which the solvophobic block length of B is longer than that of C. Morphological phase diagrams of these three ABCA tetrablock copolymers in A-selective solvents are provided and discussed in details. Moreover, the kinetic formation pathways of several typical micelle morphologies obtained from A₂B₈C₄A₂ tetrablock copolymers are as well presented and discussed.

3.1. Morphological phase diagram as a function of ε_CS and r for A₂B₆C₆A₂ tetrablock copolymers

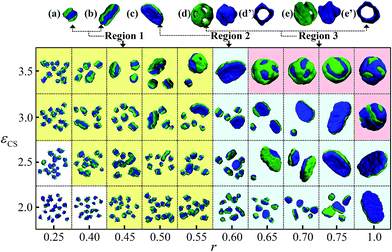
The solvent–block interaction, especially the solvophobic interaction of solvophobic blocks, is crucial to the micelle morphologies of block copolymers.²⁷ According to previous Monte Carlo study,⁴⁶ changing the solvophobic interaction of solvophobic blocks usually has an equivalent effect with changing the species or tuning the content of selective solvents in experiment to adjust micelle morphologies. Therefore, the investigation of the effects of the solvophobic interaction of solvophobic blocks on micelle morphology is important. The solvophobic interaction of block C (ε_CS) and the solvophobic interaction difference between blocks B and C (which is measured by the ratio of the solvophobic interaction of blocks B to C, i.e., r = ε_BS/ε_CS) are changed and investigated preferentially in this study.

Fig. 1 gives the morphological phase diagram of A₂B₆C₆A₂ tetrablock copolymers as a function of ε_CS and r. It is noticed that the images in the phase diagrams in Fig. 1, 4 and 5 are showing the whole simulation box for a given set of ε_CS and r. The solvophilic block A in the micelles formed by A₂B₆C₆A₂ tetrablock copolymers always tends to locate on the surface of the micelles (or both outer and inner surfaces of the vesicles) due to its solvophilic interaction and incompatibility with other blocks. Examples illustrating the distribution of blocks A are shown in Fig. S1a and b in the ESI.† In order to observe the solvophobic parts clearly, the blocks A are not shown for all the figures in this paper if not specified and the insoluble blocks B and C are respectively drawn in green and blue. In addition, there are two kinds of solvophobic compartments in the micelles formed by ABCA tetrablock copolymers are frequently mentioned in the following discussions. They are composed by B and C blocks, respectively. Therefore the two compartments are defined as B and C compartments for the purpose of clarify. From Fig. 1 it can be seen that five typical micelles, i.e., hamburger sphere (Fig. 1a), hamburger rod (Fig. 1b), Janus lamella (Fig. 1c), and asymmetric vesicles with multicompartment solvophobic layers (Fig. 1d and e), can be obtained via changing ε_CS and r. In order to identify the formation conditions of different micelle morphologies, the phase diagram shown in Fig. 1 is roughly divided into four regions, which are marked with different colors. It can be seen that when r ≤ 0.55, the A₂B₆C₆A₂ tetrablock copolymers tend to form hamburger-like micelles, which are shown in the yellow region 1 in Fig. 1. In this region, an increase in ε_CS can only result in small morphological change from spheres to short rod, while the micro-phase structure (i.e., the hamburger-like structure) of the micelles remain unchanged. However, when r becomes larger, the micro-phase structure of micelles turns to be Janus-like, and the micelle morphologies turn to be lamellas for most cases shown in region 2 (the blue region in Fig. 1) when ε_CS is relatively small. It can be seen that if r and ε_CS are both very large, the A₂B₆C₆A₂ tetrablock copolymers tend to form vesicles, as is shown in region 3 (the pink region in Fig. 1). These vesicles possess different inner and outer solvophobic layers and their solvophobic layers are multicompartment. Here we call such vesicles as asymmetric vesicles with multicompartment solvophobic layers. Fig. 1d and e are examples to illustrate the asymmetry in the solvophobic layer of the vesicle, i.e., the outer solvophobic layer is constructed by blocks B, while the inner solvophobic layer is constructed by blocks C. The vesicle cross-sections (Fig. 1d′ and e′) illustrate their hollow structures. In addition, the density distributions of different blocks and solvent in the vesicle shown in Fig. 1e are given in Fig. S1c in the ESI,† which further prove the hollow structure and the location of different blocks in the vesicle. It should be noticed that, in the case of 0.65 ≤ r < 1 in region 3, blocks B prefer to locate on the outer solvophobic layer of the vesicle. This is mainly because ε_BS is smaller than ε_CS. However, in the case of r = 1 in region 3, due to the same solvophobic interactions of blocks B and C, the probability for either blocks B or C locating on the outer solvophobic layer is equal.³² The images of the vesicles with r = 1, ε_CS = 3.0 and 3.5 shown in Fig. 1 only give one situation (i.e., blocks C locating on the outer solvophobic layer) as an example. In addition, in the case of small ε_CS and r (the white region in Fig. 1), ε_BS (ε_BS = ε_CS × r) is rather small, indicating that the solvophobic interaction of blocks B is rather weak. In that case, blocks B cannot aggregate into dense solvophobic parts, meaning that multicompartment micelles can hardly be obtained in this region. Moreover, the phase diagram shown in Fig. 1 has been simulated for additional two times using different initial states. The simulation results (Fig. S3 and 4 in the ESI†) are quite similar to those shown in Fig. 1, which indicates that the simulation results observed in Fig. 1 are reliable.

Fig. 1 Morphological phase diagram of A₂B₆C₆A₂ tetrablock copolymers as a function of ε_CS and r. Four regions for different types of micelle morphologies are marked with different colors, respectively. Typical micelle morphologies for region 1 (a) and (b), region 2 (c) and region 3 (d) and (e) are given on the top of the phase diagram. The blocks B and C are respectively drawn for the vesicles shown in (d) and (e). The cross-sections (d′) and (e′) of the inner layer of the vesicles are drawn to show their hollow structures. The insoluble blocks B and C are drawn in green and blue, and the soluble blocks A are not shown in the images.

In order to elucidate the formation mechanism of different micelle morphologies, the specific surface area for micelles with different morphologies shown in Fig. 1 are calculated. The Minkowski functionals, which are proven to be valuable for the description of complex morphologies in phase separating block copolymer systems,^47,48 are employed to calculate the volume (V) and the surface area (S) of micelles, and herein obtain the specific surface area (S/V). Fig. 2a shows the variations of the specific surface areas of the solvophobic parts in the micelles formed by A₂B₆C₆A₂ tetrablock copolymers with r at ε_CS = 2.0 and ε_CS = 3.5, respectively. The specific surface areas are averaged over three independent simulations which start from different initial states. Several typical micelle morphologies are also given in Fig. 2a for the purpose of comparison. From Fig. 2a, it can be seen that the specific surface area decreases significantly with an increase in r and ε_CS. This indicates that the aggregates formed by the tetrablock copolymers tend to decrease their surface area to reduce their contact with solvents when increasing r and ε_CS. At the same time, it can be seen from Fig. 2a that the small spheres (Fig. 2a₁) have the largest specific surface area, while the vesicle (Fig. 2a₆) has the smallest specific surface area. This explains why the small spheres are observed when r and ε_CS are small, and why the vesicles are observed when r and ε_CS are rather large in the phase diagram shown in Fig. 1. In addition, the specific surface areas for B (Fig. 2b) and C (Fig. 2c) compartments in the micelles formed by A₂B₆C₆A₂ tetrablock copolymers with r at ε_CS = 2.0 and ε_CS = 3.5 are calculated, respectively. Note that the values of S/V shown in Fig. 2b and c are larger than that shown in Fig. 2a, which is mainly because the interface areas between B and C compartments are included additionally when we calculate the surface areas of B (or C) compartment. It can be seen that the specific surface areas of B compartment are decreased significantly with increasing r, whereas the decreasing tendency of the specific surface areas of C compartment is not obvious. This indicates that the decrease of the specific surface areas with increasing r shown in Fig. 2a mainly results from the decrease of the specific surface area of B compartment. It is noteworthy that previous experimental⁴⁵ and simulation⁴⁶ investigations on AB diblock copolymer micelles have proposed a similar viewpoint that the morphological transition from sphere to vesicle is mainly due to the fact that polymers need to reduce their surface area that come into contact with solvents and then reduce the free energy of the systems. However, it is difficult to calculate and quantitatively compare the surface areas between different micelles in previous studies. Our simulation results may provide a feasible way for calculating the surface area of complex micelles.

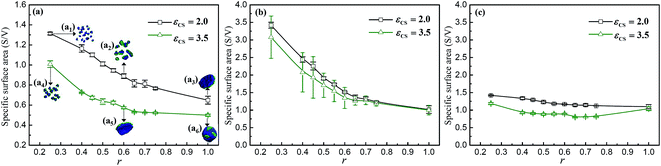Fig. 2 Variations of the specific surface areas of the micelles (a), B compartment (b) and C compartment (c) formed by A₂B₆C₆A₂ tetrablock copolymers with r at different values of ε_CS. For clarity, typical micelle morphologies (a₁)–(a₆) for different values of ε_CS and r are also given. The color coding of the images is the same as that in Fig. 1.

To further elucidate the formation of micro-structures of the micelles, the mean square end-to-end distances (〈R²_BC〉) of the solvophobic part B–C of the A₂B₆C₆A₂ tetrablock copolymers are calculated, and the values of 〈R²_BC〉 are averaged over three independent simulations starting from different initial states. Fig. 3a and b shows the variations of 〈R²_BC〉 with r at different ε_CS. It can be seen that 〈R²_BC〉 significantly increases with an increase in r when ε_CS = 2.0 (Fig. 3a). Meanwhile, the increase in 〈R²_BC〉 with r can also be seen in the case of ε_CS = 3.5 (Fig. 3b) when r ≤ 0.60. The small value of 〈R²_BC〉 indicates that the solvophobic blocks in the micelles are folded in most cases, whereas the large value of 〈R²_BC〉 means that the solvophobic blocks tend to be stretched. The distributions of R²_BC in the cases of r = 0.25 (with the minimum 〈R²_BC〉) and r = 0.60 (with the maximum 〈R²_BC〉) shown in Fig. 3b are also calculated and given in Fig. 3c and d, respectively. The peak positions observed in Fig. 3c (i.e., R²_BC = 15) and Fig. 3d (i.e., R²_BC = 55) confirm the chain conformation in the above two cases. Moreover, images for typical single chain and multi-chain aggregate are also drawn in Fig. 3c and d for illustrating the micro-structure. It is seen that the A₂B₆C₆A₂ chains tend to be folded (Fig. 3c₁) in the case of small r, which is consistent with the distribution of R²_BC shown in Fig. 3c. These folded chains tend to self-assemble into micelles with blocks C locating in the central part of the aggregate (Fig. 3c₂ gives a morphological snapshot of 12 folded chains as an example) to prevent the contact between blocks C and solvents due to the larger solvophobic interaction difference between blocks B and C (r = ε_BS/ε_CS = 0.25). However, because the solvophilic blocks A (the light grey parts shown in Fig. 3c₂) are covalently bonded at the end of blocks C, block C domains cannot be completely wrapped up by blocks B, and therefore the hamburger-like micelles in which the blocks C are partly covered by blocks B tend to be formed in the case of small r. On the contrary, the A₂B₆C₆A₂ chains tend to be stretched (Fig. 3d₁) in the case of large r. These stretched chains tend to form the Janus-like micelles (Fig. 3d₂ gives a morphological snapshot of 20 stretched chains as an example) in which both blocks B and C have relatively equal probabilities for coming into contact with solvents due to the small solvophobic interaction difference between blocks B and C (r = ε_BS/ε_CS = 0.60). On the other hand, a decrease in 〈R²_BC〉 can be seen from Fig. 3b when r is further increased from 0.60 to 1.0 in the case of ε_CS = 3.5. A further increase in r results in an increase in the solvophobic interaction of blocks B. To reduce the contact between blocks B and solvents, the micelle morphology changes from Janus lamella to asymmetric vesicle when r is increased from 0.60 to 1.0. Therefore, the decrease in 〈R²_BC〉 accompanied by the morphological changes indicates that the copolymer chains in asymmetric vesicles are much more bended than the chains in Janus lamella.

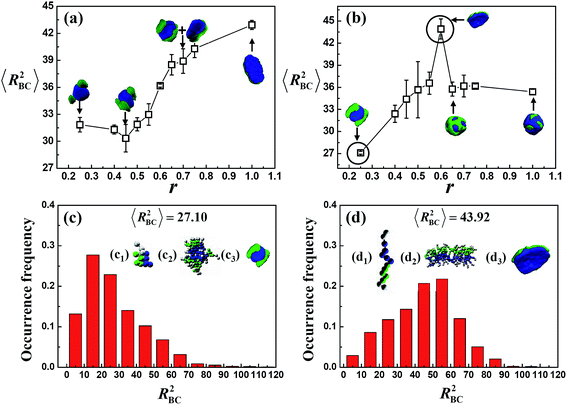Fig. 3 Variations of the mean square end-to-end distance of the solvophobic blocks of A₂B₆C₆A₂ tetrablock copolymer (〈R²_BC〉) with r when (a) ε_CS = 2.0 and (b) ε_CS = 3.5. The distributions of R²_BC for the two circled points in (b) are given in (c) and (d). Corresponding micelle morphologies, including single chain (c₁), (d₁) and multi-chain aggregate (c₂), (d₂) are given correspondingly. The color coding of the images is the same as that in Fig. 1, while the solvophilic blocks A are drawn in light gray in (c₁ and c₂), (d₁ and d₂).

From the aforementioned simulation results and discussion, it can be found that, the solvophobic interaction of blocks C (ε_CS) and the solvophobic interaction difference between blocks B and C (r) can both affect the micelle specific surface area and results in the morphological changes of A₂B₆C₆A₂ tetrablock copolymers. However, the solvophobic interaction difference between blocks B and C has a significant influence on the chain conformation of A₂B₆C₆A₂ tetrablock copolymers, and hence affects the microstructures of the micelles.

3.2. Morphological phase diagram as a function of ε_CS and r for A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers

In this subsection, the solvophobic part of the tetrablock copolymer is changed from B₆C₆ to B₇C₅ and B₈C₄, while the total length of the solvophobic blocks remains unchanged. As aforementioned, the solvophobic interaction difference between blocks B and C is defined as r = ε_BS/ε_CS, and it ranges from 0.25 to 1.0. It is noteworthy that the length of solvophobic block B is longer than the length of block C, which means that the longer solvophobic block has lower solvophobic interaction, while the shorter solvophobic block has higher solvophobic interaction. The effects of ε_CS and r on the phase behaviors of these two tetrablock copolymers, i.e., A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers, are investigated.

Fig. 4 shows the morphological phase diagram of A₂B₇C₅A₂ tetrablock copolymers as a function of ε_CS and r. Similar to the typical micelle morphologies formed by A₂B₆C₆A₂ tetrablock copolymers, hamburger sphere (Fig. 4a), Janus sphere (Fig. 4b), Janus rod (Fig. 4c), Janus lamella (Fig. 4d–e), asymmetric vesicles with multicompartment solvophobic layers (Fig. 4f and g), are obtained via adjusting ε_CS and r. Likewise, the phase diagram is roughly divided into four regions, i.e., the region for hamburger-like micelle (the yellow region in Fig. 4), the region for Janus-like micelle (the blue region in Fig. 4), and the region for asymmetric vesicle with multicompartment solvophobic layer (the pink region in Fig. 4), and the region in which multicompartment micelles can hardly be obtained (the white region in Fig. 4). The phase diagram shown in Fig. 4 illustrates that the morphological change with ε_CS and r is similar to that observed in Fig. 1. However, the region for Janus-like micelle shown in Fig. 4 is much larger than that in Fig. 1, i.e., the left boundary of the region for Janus-like micelle shifts to smaller r. As discussed in above subsection, the Janus-like micelle tends to be formed when the solvophobic interaction difference between blocks B and C is small (i.e., r is large) in A₂B₆C₆A₂ tetrablock copolymer system. The phenomenon shown in Fig. 4 that the Janus-like micelle can be formed when r is small indicates that the effect of the solvophobic interaction of the longer blocks B can be equivalent to that of the shorter blocks C when r is small in A₂B₇C₅A₂ tetrablock copolymer system. Therefore, it can be concluded that longer block length can compensate the lower solvophobic interaction of block B to a certain degree in A₂B₇C₅A₂ tetrablock copolymer system. In addition, the asymmetric vesicle with multicompartment solvophobic layer formed by A₂B₇C₅A₂ tetrablock copolymers when r = 1, ε_CS = 3.5 (Fig. 4g) is different from the one observed in A₂B₆C₆A₂ tetrablock copolymer system. In A₂B₆C₆A₂ tetrablock copolymer system, the probability for either block B or C locating on the outer solvophobic layer of the vesicle is equal when r = 1. However, due to the block length effect, the outer solvophobic layer of the A₂B₇C₅A₂ asymmetric vesicle is always occupied by the shorter blocks C. This is consistent with the simulation results for ABCA asymmetric vesicle reported by Cui et al.³²

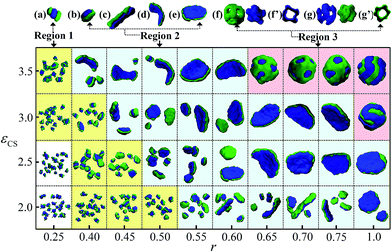Fig. 4 Morphological phase diagram of A₂B₇C₅A₂ tetrablock copolymers as a function of ε_CS and r. Four regions for different types of micelle morphologies are marked with different colors, respectively. Typical micelle morphologies for region 1 (a), region 2 (b)–(e) and region 3 (f) and (g) are given on the top of the phase diagram. The blocks B and C are respectively drawn for the vesicles shown in (f) and (g). The cross-sections (f′) and (g′) of the inner layer of the vesicles are drawn to show their hollow structures. The color coding of the images is the same as that in Fig. 1.

When the block length difference between blocks B and C is further increased (i.e., A₂B₈C₄A₂ tetrablock copolymer), the phase behavior turns to be much more different from that of A₂B₆C₆A₂ and A₂B₇C₅A₂ tetrablock copolymer. Fig. 5 shows the phase diagram of A₂B₈C₄A₂ tetrablock copolymers as a function of ε_CS and r. An obvious difference is that the region (the blue region in Fig. 5) for Janus-like micelle (Fig. 5b–g) is further increased, whereas the region (the yellow region in Fig. 5) for hamburger-like micelle is further decreased. This phenomenon indicates that a large increase in the length of block B (decrease in the length of block C) makes the effect of the solvophobic interaction of block B equivalent to that of blocks C when r is rather small. Another difference in Fig. 5 is that the Janus rod or lamella (Fig. 5d and e) formed by A₂B₈C₄A₂ tetrablock copolymers is always bended, which is quite different from the straight (or flat) ones (Fig. 1b and c) formed by A₂B₆C₆A₂ tetrablock copolymers. Actually, several Janus micelles are also bended in the case of A₂B₇C₅A₂ tetrablock copolymer (Fig. 4). However, in the case of A₂B₈C₄A₂ tetrablock copolymers, the majority Janus micelles are bended. It is noteworthy that the Janus rod-like micelle shown in Fig. 5d is quite long, flat and bended, just like a ribbon (hence, it is called Janus ribbon in the follow discussion). The formation of the bended Janus micelle is mainly because that the length of block C is shorter than the length of block B, and the shorter blocks C tend to form the inner surface of the bended Janus micelles, where the surface area is relatively small. This explains why the amount of bended Janus micelles in the case of A₂B₈C₄A₂ tetrablock copolymers is much higher than that in the case of A₂B₇C₅A₂ tetrablock copolymers. More interestingly, the short tubes (Fig. 5f and g) in which the inner and outer solvophobic layers are constructed by different solvophobic blocks can be observed in the phase diagram of A₂B₈C₄A₂ tetrablock copolymers. Moreover, it can be seen that the structures of the short tube shown in Fig. 5f and g are different from each other, i.e., the inner and outer layer of the short tube are all flat and continuous (Fig. 5f), whereas the inner and outer layer of the short tube have many bumps and pores (Fig. 5g). Due to the highly asymmetry of the solvophobic layer, the short tubes shown in Fig. 5f and g are all called short Janus tube in the following discussion. It is noteworthy that the bended Janus ribbon (Fig. 5d), bended Janus lamella (Fig. 5e), and the short Janus tubes (Fig. 5f and g) have seldom been observed in ABC linear or star terpolymer systems.

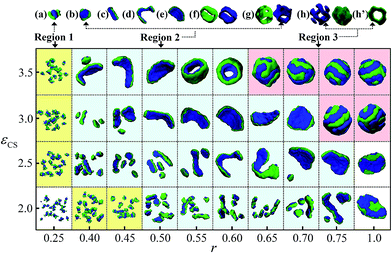Fig. 5 Morphological phase diagram of A₂B₈C₄A₂ tetrablock copolymers as a function of ε_CS and r. Four regions for different types of micelle morphologies are marked with different colors, respectively. Typical micelle morphologies for region 1 (a), region 2 (b)–(g) and region 3 (h) are given on the top of the phase diagram. The blocks B and C are respectively drawn for the micelles shown in (f)–(h). The cross-section (h′) of the inner layer of the vesicle is drawn to show its hollow structure. The color coding of the images is the same as that in Fig. 1.

The above simulation results indicate that if the longer solvophobic block has lower solvophobic interaction, while the shorter solvophobic block has higher solvophobic interaction in an ABCA tetrablock copolymer, the micelle morphologies with Janus-type solvophobic parts are the most obtainable micelle morphologies. In addition, the Janus-like micelles tend to be more and more bended when the block length difference between blocks B and C is increased. Subsequently, the phase diagrams shown in Fig. 4 and 5 were simulated for additional two times using different initial states to test whether the micelles shown in the phase diagrams are at their stable states. It is found that the phase diagrams (Fig. S5–S8 in the ESI†) are quite similar to those shown in Fig. 4 and 5. However, the Janus tubes shown in Fig. 5f and g are not obtained from initial states 2 and 3. The dependency of Janus tube on initial state is investigated in the next subsection.

It should be noticed that the ABCA tetrablock copolymers with other chain length ratios of blocks B to C have also been simulated (i.e., A₂B₄C₈A₂, A₂B₅C₇A₂, A₂B₂C₁₀A₂ and A₂B₁₀C₂A₂), and the simulation results are given in Fig. S9–S12 in the ESI.† In the case of A₂B₄C₈A₂ and A₂B₅C₇A₂ tetrablock copolymers, the shorter blocks B tend to locate at the outer surface of the micelles due to their weaker solvophobic interaction, which results in the formation of micelles with bump surface for almost all the cases shown in Fig. S9 and S10.† These micelle structures are not so interesting as those obtained from the A₂B₈C₄A₂ and A₂B₇C₅A₂ tetrablock copolymer systems shown in Fig. 4 and 5, which is the reason why we chose the A₂B₈C₄A₂ and A₂B₇C₅A₂ tetrablock copolymer systems to investigate in details. In addition, Fig. S11 and S12† shows that the tetrablock copolymers in which the length difference between blocks B and C are rather large (i.e., the A₂B₂C₁₀A₂ and A₂B₁₀C₂A₂ tetrablock copolymers) are not suitable for obtaining multicompartment micelles with distinct boundary between different compartments.

3.3. Formation pathways of several typical micelles formed by A₂B₈C₄A₂ tetrablock copolymers

The simulation results obtained in above subsection illustrate that the ABCA tetrablock copolymers with asymmetric solvophobic blocks can form many novel micelles, such as the bended Janus ribbon, the bended Janus lamella, and the short Janus tube, and so on. However, it is unclear that when the bended Janus micelle starts to be bended during its formation process. Therefore, the formation pathway of the bended Janus lamella (Fig. 5e) formed by A₂B₈C₄A₂ tetrablock copolymers is investigated.

Fig. 6a–d shows the pathway of the formation of Janus lamella (Fig. 5e) with ε_CS = 3.5 and r = 0.50. It is seen that the A₂B₈C₄A₂ tetrablock copolymers first aggregate into large aggregations in which blocks C is partially covered up by blocks B (Fig. 6a). Subsequently, the large aggregations evolve into a bended lamella (Fig. 6b). Due to micro-segregation between blocks B and C, the bended lamella further changes into a bended Janus lamella (Fig. 6c and d). Moreover, the variations of the average contact number N_BS, N_CS, and N_BC with simulation time (t) are given in Fig. 6e to further elucidate the kinetic formation pathway of the bended Janus lamella. It is seen that the values of N_BS and N_CS drop rapidly, whereas the value of N_BC increases significantly when t is increased to 1.40 × 10⁶ MCS. A decrease in N_BS and N_CS indicates that the solvophobic blocks segregate from solvent and then aggregate into micelles. An increase in N_BC indicates that the contact between blocks B and C is increased due to the aggregation of the copolymers. As simulation time t is further increased to 2.80 × 10⁶ MCS, the values of N_BS, N_CS and N_BC are all decreased. The decrease in N_BC means that the micro-segregation between blocks B and C in the micelle occurs due to the incompatibility between blocks B and C. After t = 2.80 × 10⁶ MCS, the values of N_BS, N_CS, and N_BC almost remain unchanged, which means that micelle morphology and its microstructure formed by blocks B and C are almost stable. The simulation result for the variations of N_BS, N_CS, and N_BC shown in Fig. 6e is quite consistent with the formation pathway shown in Fig. 6a–d. It is noteworthy that the lamella is formed when t is about 1.68 × 10⁶ MCS, and it is already bended at this time. Hence, the simulation result shown in Fig. 6 indicates that the lamella is bended almost as soon as it is formed.

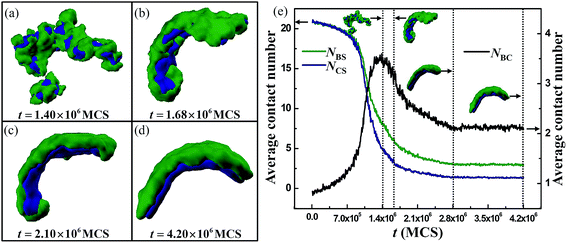Fig. 6 Morphological pathway (a)–(d) and variations (e) of the average contact number (N_BS, N_CS and N_BC) with simulation time (t) for bended Janus lamella formed by A₂B₈C₄A₂ tetrablock copolymers with ε_CS = 3.5 and r = 0.50. The color coding of the images is the same as that in Fig. 1.

On the other hand, from the simulation results shown in Fig. 5, it can be seen that when r is increased from 0.50 to 0.60, the micelle morphology formed by A₂B₈C₄A₂ tetrablock copolymers changes from the bended Janus lamella (Fig. 5e) to the short Janus tube (Fig. 5f and g). Since the region of the Janus lamella is connected with the region of the short Janus tube, we wonder whether the short Janus tube is formed via the further bending and closing of the bended Janus lamella. The pathway of the formation of the short Janus tube (Fig. 5g) with ε_CS = 3.5 and r = 0.60 is examined and shown in Fig. 7a–d. It is seen that the block copolymers first aggregate into a large vesicle in which the solvophobic blocks B and C are randomly distributed (Fig. 7a and a′). And then, due to the difference in the solvophobic interaction between blocks B and C, the blocks with lower solvophobic interaction (blocks B) gradually distribute to the outer solvophobic layer, whereas the blocks with higher solvophobic interaction (blocks C) gradually distribute to the inner solvophobic layer of the vesicle (Fig. 7b and b′). With further increase in time, the solvophobic layer of the vesicle is perforated by a pore (Fig. 7c). The pore size is gradually increased with time, and eventually the vesicle changes into a hollow short tube with different solvophobic bocks locating on the inner and outer surfaces, respectively. In order to further illustrate the changes in the pore sizes shown in Fig. 7c and d, Fig. 7e gives the variations of the polymer densities (ρ) of the Janus tubes with the radii around the Janus tubes' mass center (R) at different simulation time. It is seen that the density curves almost overlap at larger R (R > 11). This indicates that the whole size of the Janus tube remains unchanged with increasing simulation time. On the other hand, Fig. 7e also shows that the peak width of the density curve turns to be narrower with increasing simulation time. The peak width of the density curve can roughly reflect the wall thickness of the Janus tube. The result that the peak width becomes narrower indicates that the wall of the Janus tube turns to be thinner with increasing simulation time. Based on the above analysis, it can be concluded that the Janus tube turns to be thinner while its whole size remains almost unchanged with increasing simulation time, which indicates that the inner pore size of the Janus tube is increased with increasing simulation time.

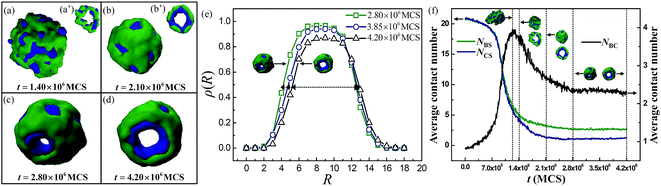Fig. 7 (a)–(d) Morphological pathway of the short Janus tube formed by A₂B₈C₄A₂ tetrablock copolymers with ε_CS = 3.5 and r = 0.60; (e) variations of the polymer densities (ρ) with the radii around the Janus tubes' mass center (R) of the Janus tubes formed at different simulation time (t); (f) variations of the average contact number (N_BS, N_CS and N_BC) with t. The cross-sections of (a) and (b) are given in (a′) and (b′), respectively. The color coding of the images is the same as that in Fig. 1.

The formation pathway shown in Fig. 7a–d indicates that the short Janus tube is actually formed by perforating the solvophobic layer of the asymmetric vesicle, rather than evolves from the bended Janus lamella. In order to further understand the formation mechanism of the short Janus tube, the variations of N_BS, N_CS, and N_BC with simulation time (t) are given in Fig. 7f. It is seen that N_BS and N_CS decrease, while N_BC first increases and then decreases with an increase in t, which is quite similar to the case shown in Fig. 6e. It can be seen from Fig. 7f that the curves of N_BS and N_CS are almost overlapped and the value of N_BC remains large when the vesicle is formed (t = 1.40 × 10⁶ MCS). Both the overlapped N_BS and N_CS curves and the large N_BC value indicate that the phase separation between blocks B and C has not started yet. This means that the formation of vesicle is faster than the micro-phase separation process between blocks B and C when the solvophobic interaction difference between blocks B and C is small (i.e., r = 0.60). A separation between the curves of N_BS and N_CS, and a considerably decrease in N_BC occurs when t is further increased from 1.40 × 10⁶ MCS to 2.10 × 10⁶ MCS, which indicates that the micro phase separation between blocks B and C in the vesicle occurs. As a result, the asymmetric vesicle with blocks C located inside and blocks B located outside is formed. When t is further increased from 2.10 × 10⁶ MCS to 2.80 × 10⁶ MCS, the values of N_BS and N_CS remain almost unchanged, whereas the value of N_BC still keeps decreasing. This means that in this time period blocks B and C continue to phase separate after the asymmetric vesicle is formed. Since the asymmetric vesicle is perforated at the end of this time period, it can be concluded that the phase separation between blocks B and C leads to the perforation of the asymmetric vesicle.

As discussed in the above subsection, the short Janus tube is depended on initial state. Therefore, different initial states are employed for searching other micelle morphologies in the case of ε_CS = 3.5 and in the vicinity of r = 0.60. Fig. 8 shows several typical micelle morphologies obtained by changing the initial state. It is seen that Janus lamella (Fig. 8a), bowl-shaped semivesicle with multicompartment solvophobic layer (Fig. 8b), short Janus tube (Fig. 8c and d) and asymmetric vesicle with multicompartment solvophobic layer (Fig. 8e) can be obtained. It should be noticed that the Janus lamella shown in Fig. 8a also evolves from the perforated asymmetric vesicle (Fig. S13 in the ESI†). Its formation pathway is quite different from the formation pathway of the bended Janus lamella shown in Fig. 6. Actually, the micelles shown in Fig. 8a–d are all formed by perforating the asymmetric vesicle. As an example, the formation pathway of the bowl-shaped semivesicle (Fig. 8b) is given in Fig. 9.

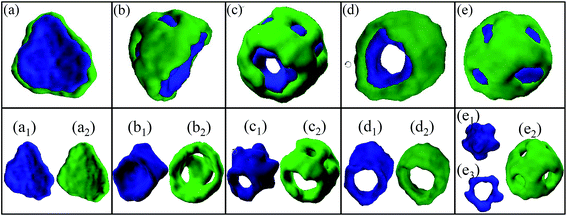Fig. 8 Typical micelle morphologies of A₂B₈C₄A₂ tetrablock copolymers with ε_CS = 3.5 obtained by changing initial states. (a) r = 0.55, (b) r = 0.60, (c) r = 0.60, (d) r = 0.63, (e) r = 0.63. (a₁)–(e₁) and (a₂)–(e₂) are the morphologies of blocks C and B, respectively. For clarity, the cross-section of the inner layer of the vesicle (e₁) is given in (e₃). The color coding of the images is the same as that in Fig. 1.

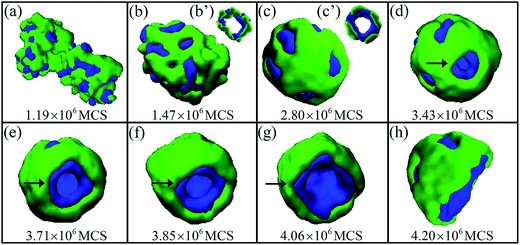Fig. 9 Morphological pathway (a)–(h) for bowl-shaped semivesicle formed by A₂B₈C₄A₂ tetrablock copolymers. For clarity, the cross-sections of the vesicles (b) and (c) are given in (b′) and (c′) respectively. The pores in the vesicles are marked by black arrows. The color coding of the images is the same as that in Fig. 1.

It is seen that the block copolymers first self-assembled into an asymmetric vesicle (Fig. 9b and c). Afterwards, a pore appears (Fig. 9d) and the pore size increases (Fig. 9e–g) with increasing simulation time, and finally a bowl-shaped semivesicle (Fig. 9h) is formed. The reason for forming various morphologies shown in Fig. 8 is mainly because the number and position of the pore appearing in the asymmetric vesicle is random. If two pores appear in the vesicle, the short Janus tube (Fig. 8c and d) with a perforated pore can be formed, whereas if one pore appears, the Janus lamella (Fig. 8a) or the bowl-shaped semivesicle (Fig. 8b) may be obtained. It is noteworthy that similar bowl-shaped semivesicles can also be obtained by ABC miktoarm terpolymers both in experiment²² and simulation.²⁷ In experiment, Lodge's group²² reported that the bowl-shaped semivesicles are mainly formed via the folding of bilayer membranes (lamella). In the current paper, the simulation result shown in Fig. 8b indicates that ABCA tetrablock copolymers can also form such bowl-shaped semivesicles. At the same time, the simulation result shown in Fig. 9 provides another possible formation mechanism of the bowl-shaped semivesicles, which is different from the one observed in ABC miktoarm terpolymer systems in experiment.²²

In addition, the formation probability (P) for the micelles with ε_CS = 3.5 and r = 0.55 − 0.63 shown in Fig. 8 is roughly calculated and shown in Table 1. The formation probability of each micelle shown in Table 1 is calculated as follows: 50 systems with the same interaction parameters but different initial states are simulated, and the numbers of the systems in which the Janus lamellas, semivesicles (or Janus tubes) and vesicles have been formed are calculated and denoted as N_L, N_SV and N_V, respectively. Then, the formation probabilities of these three kinds of micelles can be respectively calculated as: P_L = N_L/50, P_SV = N_SV/50 and P_V = N_V/50. Taking the case with ε_CS = 3.5, r = 0.55 as an example (Line 1 in Table 1), 50 systems with different initial states are simulated. There are 46 systems in which the Janus lamellas are formed, while only 4 systems in which the semivesicles are formed. Then the probabilities for forming Janus lamella is 46/50 = 92%, while that for forming semivesicle is 4/50 = 8%. From Table 1 it can be seen that the probability for forming Janus lamella is quite high when r = 0.55, whereas the probabilities for forming semivesicle and vesicle are rather low. However, when r is increased, the probability for forming Janus lamella is decreased, while the probabilities for forming semivesicle and vesicle are increased. Table 1 indicates that the semivesicle tend to be formed in the case of large r, whereas the Janus lamella tend to be formed in the case of small r.

Table 1 Probabilities for A₂B₈C₄A₂ tetrablock copolymers forming different micelle morphologies when ε_CS = 3.5, r = 0.55 − 0.63

r	Formation probability
0.55	92%	8%	0%
0.60	77%	17%	6%
0.61	70%	21%	9%
0.62	46%	34%	20%
0.63	38%	34%	28%

---

4. Conclusion

The phase behavior of the ABCA tetrablock copolymers in A-selective solvents is investigated using Monte Carlo simulation. The main focus is the effects of the solvophobic interactions of blocks B and C (ε_BS and ε_CS) on the micelle morphologies. Three kinds of ABCA tetrablock copolymers, i.e., A₂B₆C₆A₂, A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers, are considered. Phase diagrams of these three tetrablock copolymers as a function of ε_CS and r are given and discussed. It is found that r and ε_CS can both affect the specific surface area of micelles and lead to the morphological changes of ABCA tetrablock copolymer micelles. In addition, r can change the solvophobic chain conformation and hence affect the micro-structures of the solvophobic parts of the micelles. For A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers, several novel micelle morphologies, such as the bended Janus ribbon and lamella, short Janus tube, and bowl-shaped semivesicle, are obtained. Interestingly, it is found that in the phase diagrams of A₂B₇C₅A₂ and A₂B₈C₄A₂ tetrablock copolymers, the micelle type with Janus-like solvophobic parts is the majority micelle type, which mainly results from the solvophobic interaction balance between blocks B and C. The simulation result also indicates that the bended Janus lamella is formed via the aggregation of block copolymers and it is already bended when the lamella is formed. However, the short Janus tube and bowl-shaped semivesicle are all formed via perforating the asymmetric vesicle. The formation pathway of the bowl-shaped semivesicle is different from the pathway of the bowl-shaped semivesicles formed by ABC miktoarm terpolymers in experiment.²²

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China for General Program (21374118), (21474107), and Key Program (51433009). The resource provided by Computing Center of Jilin Province is gratefully acknowledged.

References

1. L. Zhang and A. Eisenberg, Science, 1995, 268, 1728–1731.
2. J. Ding and G. Liu, Macromolecules, 1997, 30, 655–657.
3. S. Jain and F. S. Bates, Science, 2003, 300, 460–464.
4. L. Wang, T. Jiang and J. Lin, RSC Adv., 2013, 3, 19481–19491.
5. A. O. Moughton, M. A. Hillmyer and T. P. Lodge, Macromolecules, 2012, 45, 2–19.
6. A. Laschewsky, Curr. Opin. Colloid Interface Sci., 2003, 8, 274–281.
7. H. Ringsdorf, P. Lehmann and R. Weberskirch, Multicompartmentation-a concept for the molecular architecture of life, in 217th ACS National Meeting, Anaheim, CA, 1999.
8. J. F. Lutz and A. Laschewsky, Macromol. Chem. Phys., 2005, 206, 813–817.
9. T. P. Lodge, A. Rasdal, Z. Li and M. A. Hillmyer, J. Am. Chem. Soc., 2005, 127, 17608–17609.
10. J. Zhu and R. C. Hayward, Macromolecules, 2008, 41, 7794–7797.
11. G.-e. Yu and A. Eisenberg, Macromolecules, 1998, 31, 5546–5549.
12. Z. Ma, H. Yu and W. Jiang, J. Phys. Chem. B, 2009, 113, 3333–3338.
13. W. Kong, W. Jiang, Y. Zhu and B. Li, Langmuir, 2012, 28, 11714–11724.
14. J. Dupont, G. Liu, K. i. Niihara, R. Kimoto and H. Jinnai, Angew. Chem., Int. Ed., 2009, 48, 6144–6147.
15. A. H. Gröschel, F. H. Schacher, H. Schmalz, O. V. Borisov, E. B. Zhulina, A. Walther and A. H. E. Müller, Nat. Commun., 2012, 3, 710.
16. A. H. Gröschel, A. Walther, T. I. Löbling, J. Schmelz, A. Hanisch, H. Schmalz and A. H. E. Müller, J. Am. Chem. Soc., 2012, 134, 13850–13860.
17. F. Schacher, A. Walther and A. H. E. Müller, Langmuir, 2009, 25, 10962–10969.
18. F. Schacher, A. Walther, M. Ruppel, M. Drechsler and A. H. E. Müller, Macromolecules, 2009, 42, 3540–3548.
19. J. Xin, D. Liu and C. Zhong, J. Phys. Chem. B, 2009, 113, 9364–9372.
20. Y. Zhu, X. Yang, W. Kong, Y. Sheng and N. Yan, Soft Matter, 2012, 8, 11156–11162.
21. Z. Li, E. Kesselman, Y. Talmon, M. A. Hillmyer and T. P. Lodge, Science, 2004, 306, 98–101.
22. Z. Li, M. A. Hillmyer and T. P. Lodge, Nano Lett., 2006, 6, 1245–1249.
23. Z. Li, M. A. Hillmyer and T. P. Lodge, Langmuir, 2006, 22, 9409–9417.
24. N. Saito, C. Liu, T. P. Lodge and M. A. Hillmyer, Macromolecules, 2008, 41, 8815–8822.
25. C. Liu, M. A. Hillmyer and T. P. Lodge, Langmuir, 2009, 25, 13718–13725.
26. C.-I. Huang, C.-H. Liao and T. P. Lodge, Soft Matter, 2011, 7, 5638–5647.
27. W. Kong, B. Li, Q. Jin, D. Ding and A.-C. Shi, J. Am. Chem. Soc., 2009, 131, 8503–8512.
28. A. Touris, S. Chanpuriya, M. A. Hillmyer and F. S. Bates, Polym. Chem., 2014, 5, 5551–5559.
29. Y. Matsuo, R. Konno, T. Ishizone, R. Goseki and A. Hirao, Polymers, 2013, 5, 1012–1040.
30. E. D. Gomez, T. J. Rappl, V. Agarwal, A. Bose, M. Schmutz, C. M. Marques and N. P. Balsara, Macromolecules, 2005, 38, 3567–3570.
31. A. K. Brannan and F. S. Bates, Macromolecules, 2004, 37, 8816–8819.
32. J. Cui and W. Jiang, Langmuir, 2011, 27, 10141–10147.
33. M. J. Greenall and C. M. Marques, Phys. Rev. Lett., 2013, 110, 088301.
34. I. Carmesin and K. Kremer, Macromolecules, 1988, 21, 2819–2823.
35. R. Larson, J. Chem. Phys., 1989, 91, 2479.
36. R. Larson, J. Chem. Phys., 1992, 96, 7904.
37. J. I. Siepmann and D. Frenkel, Mol. Phys., 1992, 75, 59–70.
38. D. Frenkel, G. C. A. M. Mooij and B. Smit, J. Phys.: Condens. Matter, 1991, 4, 3053–3076.
39. W. Hu, J. Chem. Phys., 1998, 109, 3686.
40. K. Haire, T. Carver and A. Windle, Comput. Theor. Polym. Sci., 2001, 11, 17–28.
41. S. Ji and J. Ding, Langmuir, 2006, 22, 553–559.
42. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087.
43. R. G. Larson, J. Chem. Phys., 1992, 96, 7904–7918.
44. W. Kong, B. Li, Q. Jin and D. Ding, Langmuir, 2010, 26, 4226–4232.
45. H. W. Shen and A. Eisenberg, J. Phys. Chem. B, 1999, 103, 9473–9487.
46. P. C. Sun, Y. H. Yin, B. H. Li, T. H. Chen, Q. H. Jin, D. T. Ding and A. C. Shi, J. Chem. Phys., 2005, 122, 204905.
47. G. J. A. Sevink and A. V. Zvelindovsky, J. Chem. Phys., 2004, 121, 3864–3873.
48. K. Michielsen and H. de Readt, Phys. Rep., 2001, 347, 461–538.

---

Footnote

† Electronic supplementary information (ESI) available: Simulation results illustrate the distribution of solvophilic blocks A in the micelles, additional simulation results obtained from different initial states and other chain length ratios of blocks B to C, and the formation pathway of the Janus lamella in Fig. 8a. See DOI: 10.1039/c5ra11865d

---