Enthalpy–entropy relations in the acid–base equilibrium of warfarin and 10-hydroxywarfarin; joint experimental and theoretical studies

Abstract

In this work we delineate basic thermodynamic factors that govern the acid–base equilibrium of the phenolic drug warfarin, pK_a = 4.99, and its metabolite 10-hydroxywarfarin, pK_a = 5.95. By applying experimental and theoretical approaches we have determined the enthalpic and entropic contributions to the dissociation free energy for both molecules. We have found that formation of specific intramolecular hydrogen bonds: OH⋯O by warfarin and OH⋯OH⋯O by 10-hydroxywarfarin, respectively, may be of a great importance for the changes in enthalpy and entropy during dissociation. The Car–Parrinello molecular dynamics have shown that these bonds are present at both temperatures T = 298 K and T = 378 K. We infer that an uncommon double bridge of 10-hydroxywarfarin, OH⋯OH⋯O, imposes lower flexibility on the molecule and thereby a stronger rise of heat capacity and enthalpy upon dissociation than the single OH⋯O bond noted for warfarin. It has been proposed, in addition, that the entropic contributions derive from the two opposite effects related to: solvation of ions – it leads to a loss of entropy, and breaking of intramolecular bonds – it causes a gain of entropy. For 10-hydroxywarfarin these effects seem to be equal in magnitude, and thereby, its dissociation entropy is close to zero. Furthermore, we show that addition of a surfactant and aprotic cosolvent changes the enthalpy–entropy relations and induces the upward pK_a shifts of both molecules, up to 1.5 pH unit. The changes in thermodynamics which are caused by these two additives are, however, totally different.

---

1 Introduction

A sizeable part of organic molecules possess ionizable acidic or basic functional groups that are characterized by the acid dissociation constant K_a, normally expressed as the logarithmic constant pK_a.¹ These values determine the fundamental physicochemical properties of molecules, like polarity, water solubility, membrane permeability, polarizability, or capability of interactions with other molecules. Acid–base properties account thereby for activity and functionality of compounds, both naturally occurring endogenous compounds as well as xenobiotics, e.g. drugs. Bioavailability of therapeutics is often strictly dependent on their ionization state, so on their pK_a.² Therefore, determination of pK_a is an initial and crucial step during the development of new biologically active molecules.

In spite of a huge number of reports on pK_a values determined for a variety of compounds, there are relatively few works showing explicit relationships between molecular structure, changes of enthalpy and entropy during dissociation, and given pK_a values. Some information may be however relatively easily gained by determining pK_a at different temperatures. Thermal variation of pK_a indicates a direction of heat energy transfer during dissociation, i.e. exo- or endothermicity of the process, and it enables calculation of the enthalpic (ΔH) and entropic (ΔS) contributions to dissociation energy from the van't Hoff model. It is to be highlighted that thermodynamic characterization of acid dissociation equilibrium is pivotal for understanding of basic effects and interactions that govern ionization state of molecule and its specific activity. Hence, it is obvious that this knowledge is also of great importance for designing of new molecules with predictable properties, e.g. new drugs. It is also crucial for development of modern strategies of supramolecular pK_a tuning, which makes up one of the most promising concepts in current supramolecular chemistry.^2–14 In these systems such issues as intrinsic flexibility, molecular strain, intramolecular interactions, or specific relations with nearby solvent molecules, may be decisive factors for direction and magnitude of final pK_a shifts. Their role may be recognized, at least partially, by discovering correlations between molecular structure and given ΔH/ΔS values.

Warfarin (WAR) is a phenolic drug, pK_a = 4.99, widely used as an anticoagulant which prevents formation of blood clots in cardiovascular vessels.^15,16 In vivo it is metabolized to several structurally different hydroxywarfarins, from which 10-hydroxywarfarin (W10) exhibits the most specific properties. Despite having second hydroxyl group W10 undergoes only single dissociation, due to aliphatic nature of the second –OH group. We have found in our recent work that WAR and all hydroxywarfarins are prone to form the single intramolecular hydrogen bond involving the ionizable hydroxyl group OH⋯O, except W10, for which an uncommon double bridge involving the second hydroxyl group OH⋯OH⋯O has been identified.⁸ To illustrate this, we have depicted these structures in Fig. 1. Stronger stabilization of the proton by the characteristic double hydrogen bonding of W10 was proposed as the reason for its higher pK_a (5.95) comparing to the other hydroxywarfarins (4.97–5.16).¹⁷ This elevated value, as it was also remarked, may contribute to appreciably lower polarity of W10 in urine (pH around 5) than its parent drug and the other metabolites. More interestingly, we studied the pK_a shifts of WAR and W10 induced by complexation with methyl-β-cyclodextrin.⁸ For WAR they occurred to be spectacularly large, around 1.50 and 1.25 pH unit for the two enantiomers, respectively, whereas for W10 they turn out to be very small, barely measurable. It must be further emphasized that the acid–base equilibrium of WAR and W10 merits deeper investigation, in order to explain what is the background for such different properties observed between such similar molecules.

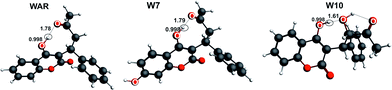Fig. 1 The structures of warfarin (WAR), 7-hydroxywarfarin (W7) and 10-hydroxywarfarin (W10) obtained from ADF/DFT/BLYP-D3/TZP calculations.¹⁷ Selected distances are in Å units.

To this end, we have decided to determine for the first time the values of standard dissociation enthalpy – ΔH° and entropy – ΔS°, for WAR and W10, and afterwards, to interpret them in terms of specific structural effects. We have also used 7-hydroxywarfarin (W7) as the reference compound, to verify whether and how hydroxylation site has any impact on dissociation thermodynamics. In particular, we wanted to evaluate the contribution of specific intramolecular interactions to dissociation thermodynamics,^18–24 and check, whether manipulations in solvent composition by addition of different modifiers: surfactant and cosolvent, affect dissociation enthalpy and entropy.^25,26 For that purpose, we have used the capillary electrophoresis with the DAD detection as an experimental tool. We have chosen this technique owing to its accuracy, easy automation, and minimization of sample and buffer consumption.²⁷ In parallel, ΔH° and ΔS° have been obtained theoretically, by using computational methods. As a result, the acid–base properties of WAR and W10 have been rationalized and logically connected with the basic thermodynamic forces that govern their dissociation equilibrium.

2 Methodology

2.1 Materials

Warfarin (WAR), the racemic mixture, was supplied by Sigma-Aldrich (St. Louis, MO, USA), 7-hydroxywarfarin (W7) and 10-hydroxywarfarin (W10), the racemic mixtures, were supplied by LGC Standards (Teddington, UK). All other chemicals were supplied by Avantor Performance Materials Poland. S. A. (Gliwice, Poland). All standard solutions were prepared in the deionized water (MilliQ, Merck-Millipore Billerica, MA, USA) and filtered through the 0.45 μm regenerated cellulose membrane, then degassed by centrifugation. The standard concentration of analytes in injected samples was 0.2 mg mL⁻¹. All analytes were dissolved in water/methanol (1 : 1 v/v) mixture to prepare the stock solution of concentration 1 mg mL⁻¹, then further dilution was made by mixing of the proper stock solution volumes with deionized water and electroosmotic flow (EOF) marker. Dimethyl sulfoxide (DMSO) was used as the EOF marker in final 0.2% (v/v) concentration.

2.2 Instrumentation

Experiments were performed on the P/ACE MDQ Capillary Electrophoresis (CE) System (Beckman Coulter, Brea, CA, USA) equipped with a diode array detector (DAD). The bare fused-silica capillaries of 60 cm total length, 50 cm effective length and 75 μm internal diameter were used. Sample injection was conducted using forward pressure 0.5 psi for 4 s. During separations, 30 kV voltage (normal polarity) and the additional forward pressure of 0.3 psi were applied. Capillary was conditioned at given temperatures (15 °C, 20 °C, 25 °C, 30 °C and 40 °C) using the liquid cooling system. Every time by using DAD detector the whole absorbance spectra were collected between 200–600 nm. Signal recorded at 282 nm and 306 nm was used for the further analysis. Each separation has been made in triplicate.

The capillary rinsing between runs was conducted applying pressure of 20 psi (1379 kPa) of 0.1 M NaOH for 1 min, and 20 psi of background electrolyte (BGE) for 2 min. During the first use of the capillary at a working day: 20 psi of methanol for 5 min, 20 psi of 0.1 M HCl for 2 min, 20 psi of deionized water for 2 min, 20 psi of 0.1 M NaOH for 10 min, and 20 psi of BGE for 10 min was applied. For the fresh capillary conditioning, the latter sequence was used but the duration of each individual step was doubled.

2.3 Buffering solutions

The BGEs of the same ionic strength 100 mM were prepared according to the receipts given in Table 1. For separations, the BGEs were diluted to 25 mM ionic strength by mixing with deionized water. In the particular cases the buffers were enriched by addition of sodium dodecyl sulfate (SDS) at final concentration of 10 mM or acetonitrile (ACN) at final concentration of 15% (v/v). Every time the pH value was measured after mixing of all constituents, prior electrophoretic analysis.

Table 1 Composition and predicted pH of all BGEs prepared for experiments, calculated for 50 mL total volume and 100 mM ionic strength^a

pH	Buffer composition [mL]
Phosphate buffer I	H3PO4 (100 mM)	NaH2PO4 (100 mM)
a The above data were obtained from the PHoEBuS 1.3 software by Analis (Namur, Belgium).
2.50	18.52	4.80
3.50	1.83	4.98

---

Acetic buffer	CH3COOH (500 mM)	CH3COONa (500 mM)
4.50	14.16	10.00
5.00	4.48	10.00
5.50	1.42	10.00

---

Phosphate buffer II	NaH2PO4 (100 mM)	Na2HPO4 (100 mM)
6.00	3.59	4.70
6.50	2.23	9.24
7.00	1.01	13.29
8.00	0.12	16.25

---

Borate buffer	Na2B4O7·10H2O (50 mM)	NaOH (1 M)
9.20	48.42	0.16
11.00	25.05	2.50

---

2.4 Methods of pK_a determination

The values of pK_a were determined by using the two different capillary electrophoretic methods: one based on effective electrophoretic mobilities (the capillary zone electrophoresis-based method, CZE) and another one based on changes in absorbance spectra (the diode array detector-based method, DAD). In the CZE method the plots of effective electrophoretic mobilities (μ_eff) values versus pH were used to sigmoidal function fitting (by OriginPro 9.1 software by OriginLabs, USA) and finding the inflection point indicating the value of pK_a, according to the equation:where α is a fitting parameter.

The values of μ_eff were obtained from the following equation:

where μ_eff and μ_obs are the effective and observed electrophoretic mobilities of analyte (m² V⁻¹ s⁻¹), respectively; μ_eof is the mobility of electroosmotic flow (m² V⁻¹ s⁻¹); L_tot and L_eff are the total and effective capillary lengths (m), 0.60 m and 0.50 m, respectively; V is the separation voltage (V); t_obs is the measured migration time of analyte (s), while t_eof is the time measured for neutral marker of EOF–DMSO (s).

In the DAD method the values of absorbance recorded at the maxima of electrophoretic peaks were used in calculation of the β parameter, defined by equation:

where A₂₈₂ and A₃₀₆ are the values of absorbance at the given wavelengths (nm).

Due to different shapes of spectra of the neutral and ionized forms of WAR, W7 and W10, the value of β changes with growing ionization of analyte (growing pH) similarly as the value of μ_eff. Then, the values of β were processed analogously to μ_eff including their plotting versus pH, function fitting of the same type and finding of inflection point indicating pK_a. In our recent work we proved that both methods are mutually consistent and give very similar pK_a values, and that they can be used interchangeably according to the current needs.¹⁷ Fig. 2 demonstrates both approaches.

Fig. 2 The relation between μ_eff or β values and pH obtained for W10 at 288 K, for CZE and DAD methods.

The temperature variations of pK_a presented in this work were calculated based on CZE method, while DAD method was applied as a reference approach in order to confirm crucial observations. It is to be noted that in all cases both methods yielded very similar pK_a values (see Fig. 2), and all qualitative trends observed between different compounds and medium types were also consistent. Exceptionally, CZE could not be applied for the micellar system containing SDS due to modification of charge caused by ionized SDS molecules. Interactions between analyte molecules and micelles resulted in the distorted relations between μ_eff and pH. In this case the values of thermodynamic parameters have been determined by using DAD method. CZE method was applicable in all other cases.

2.5 Calculation of ΔH° and ΔS°

The values of standard dissociation enthalpy – ΔH° (J mol⁻¹) and entropy – ΔS° (J mol⁻¹ K⁻¹) were calculated from the van't Hoff model describing the relation between pK_a and temperature:where R is the gas constant (8.3145 J mol⁻¹ K⁻¹).

Accordingly, the pK_a values determined at various temperature were plotted against the inverse absolute temperature (1/T) and fitted by the linear function y = b₀ + b₁x. Subsequently the ΔH° and ΔS° terms were calculated from the slope and intercept, respectively.

2.6 Computational methods

The static DFT calculations were performed by means of Gaussian 09-D0.1 program²⁸ based on BLYP-D3/6-31+*. The geometries were at first point optimized in the gas phase at BLYP-D3/6-31*+. We used such computational details because it was shown that BLYP-D3 performs well for systems containing non-covalent interactions.^29,30 Then the water solvent effects were included via the conductor polarizable continuum model (CPCM). In order to estimate pK_a values as well as the corresponding thermodynamic contributions we have applied so called the proton exchange scheme as depicted in Fig. 3. It was demonstrated that it provides reasonable estimations of pK_a values.³¹ As HW in the cycle we abbreviated the WAR derivatives. The “gas” and “aq” denote the calculations in the gas phase and the water solvent, respectively. In order to obtain the thermodynamic data for WAR and W10, solvation energies and gas phase dissociation energy has been calculated, and subsequently used in the equation shown in Fig. 3. The obtained ΔH_aq (or ΔS_aq) is a difference between enthalpies (or entropies) of deprotonation in solvent of WAR derivative (HW) and a reference molecule (HRef), in this case W7. The correct absolute value of ΔH for WAR and W10 is the sum of ΔH_aq and ΔH_ref. The UAKS and UFF atomic radii were used for determining the solvent cavity as suggested in literature.³¹ All necessary terms of the cycle can be found in ESI file Section 1.†

Fig. 3 The proton exchange scheme³¹ applied in DFT calculations of thermodynamic properties.

We have further characterized the electronic structure (see point 2 in the ESI file†) as well as the conformational stability of WAR and W10 at gas phase by molecular dynamics simulations at the DFT level within Car–Parrinello approach, as implemented in CPMD software package.^32–37 The plane wave basis set with cutoff energy of 100 Ry, within a cubic cell, 16 Å in length were applied. The temperature values T = 298 K and T = 373 K have been controlled via Nosé–Hoover chain thermostat.^27–32 Valence electrons have been treated explicitly within the DFT formalism employing the PBE exchange–correlation functional with inclusion of Grimme dispersion correction (D3), whereas, for inner electrons description, the Goedecker type pseudopotentials have been used.^32–37 All the animations presenting CPMD trajectories are available as ESI files.† VMD software package³⁷ have been used for preparation of each animation. The lengths of simulations were between 20–30 ps.

3 Results and discussion

3.1 Experimental determination of ΔH° and ΔS°

The temperature variations of pK_a in the range between 288 K and 313 K have been determined for WAR and their two derivatives: W7 and W10. W7 has been applied as the reference molecule for W10, to better understand the effect of hydroxylation site. W7, contrary to W10, exhibits similar pK_a value to WAR and its intramolecular hydrogen bonding OH⋯O is also similar in nature to the parent drug. The pK_a variations obtained for these compounds, the related values of ΔH° and ΔS°, and the structural formula of all molecules have been presented in Fig. 4. It is seen that ΔH° is positive for all three compounds, and this observation indicates that dissociation of proton in aqueous medium is endothermic. Similar ΔH° value has been obtained for WAR and W7, however, the two times higher value has been obtained for W10. The negative and also similar values of ΔS° are observed for WAR and W7, and it points that in these cases the system entropy decreases after dissociation. Interestingly, for W10 the ΔS° value is close to zero. This suggests that certain effect neutralizes the loss of entropy in this case. One should note also, based on the changes in ΔH° and ΔS° between WAR/W7 and W10, that a compensatory enthalpy–entropy relationship is noted.

Fig. 4 The van't Hoff plots obtained for WAR, W7 and W10 in aqueous medium, together with the structural formulas of given compounds and the obtained values of thermodynamic parameters.

3.2 Theoretical characterizations of WAR and W10

We have also performed theoretical calculations of the enthalpic and entropic contributions to dissociation free energy of WAR and W10, for which substantial differences have been observed in the experiments. It is seen from Fig. 5 that notably higher positive ΔH° value is observed for W10, by +20.65 kJ mol⁻¹ at CPCM/UFF level of calculations, as related to WAR. For comparison, the shift observed in experiment is +17.4 kJ mol⁻¹. One must emphasize that the calculated value of 33.1 kJ mol⁻¹ obtained for W10 agrees almost quantitatively with the experimental estimation 34.3 kJ mol⁻¹. Moreover, the qualitative picture of an increase in ΔS° values, from −9.98 J mol⁻¹ K⁻¹ for WAR up to −6.50 J mol⁻¹ K⁻¹ for W10, is consistent with the experiment, though, the agreement is less satisfactory as in absolute sense the ΔS° should vanish for W10. One could comment that other theoretical approaches, e.g. SM8T solvation model, could likely provide more accurate thermodynamic properties as it was the case for amines or carboxylic acids.³⁸ Nevertheless, the findings obtained in both experimental and theoretical approaches herein indicate explicit and unequivocal differences between WAR and W10. Based on our recent works we have found,^8,17 that formation of the intramolecular hydrogen bonding might be the key factor in this phenomenon.

Fig. 5 The DFT/BLYP-D3/6-31+* optimized ground state structures of WAR and W10 based on Gaussian 09-D0.1 program. The dissociating protons are marked by circle. In addition the selected distances of intramolecular hydrogen bonds OH⋯O are presented together with the values of thermodynamic parameters.

It is important to emphasize that at two different temperatures, 298 K and 373 K, the intramolecular interactions of WAR and W10 have turned out to be similarly stable, as indicated by the ab initio CPMD simulations. Both WAR and W10 do not undergo any spontaneous conformational transition during the simulations, and therefore, both intramolecular bridges are preserved in these conditions; see the animations entitled war25.mpg, war100.mpg, W10-25.mpg and W10-100.mpg (attached as ESI files†). These results clearly show that both systems are inherently stable at free energy level, not prone to any spontaneous transitions. It proves also that endothermicity of dissociation is not related to breaking of these bonds during increase in temperature, but most likely, to their breaking upon hydrogen bonding interaction with solvent water molecules. In addition, one shall note that the intramolecular bond is stronger for W10 (shorter O⋯H bond, by ∼0.1 Å), what qualitatively explains why in this case the higher pK_a is observed as compared with WAR.

One should admit that the conjugate base of W10 can also be stabilized by the intramolecular hydrogen bonding O⁻⋯HO, causing a drop of its pK_a value comparing to WAR. Nevertheless, this potential effect is apparently weaker than stabilization of the non-ionized form by the double intramolecular bridge OH⋯OH⋯O. One should add moreover that the higher deprotonation energy of W10 over WAR is also valid at gas-phase level of calculations. Finally, one should mention that Mishra and coworkers³⁹ and also Regaldo et al.⁴⁰ have modeled the spectroscopic properties of WAR and its derivatives. The authors of the latter work have also noticed, based on static DFT/B3LYP calculations, that the neutral forms of these compounds can possess the intramolecular hydrogen bonds OH⋯O.

3.3 Enthalpy–entropy relationships

We are able to propose the most likely explanation for the obtained findings. Owing to the similar results obtained for WAR and W7 one should state, that hydroxylation site is essential for dissociation thermodynamics. Formation of the double hydrogen bonding by W10 seems to be the crucial factor which distinguishes this molecule from both WAR and W7. Accordingly, one could further state that appreciably higher ΔH° noted for W10 might stem from the fact that the double intramolecular hydrogen bonding affects the total degree of freedom of the molecule, thus also its heat capacity, stronger than the weaker single bond noted for WAR and W7. It seems to be very probable that transfer of proton from the functional group involved in intramolecular bonding to solvent molecules entails disconnection of particular molecule sites, and thus, causes also release of molecular strain and rise of conformational flexibility. This imposes positive ΔH° and endothermicity of the process for all molecules, however, the most strongly for W10 where the double OH⋯OH⋯O is noted. Due to this specific linkage, also the number of ways in which the neutral molecule of W10 may be arranged in space is lower, thereby its entropy is also lower comparing to WAR and W7. It is important that after dissociation the created ions become solvated and order water dipoles reducing their entropy, what is energetically unfavourable effect. However, concurrently, this effect is balanced by the breaking of intramolecular bonding organizing the arrangement of atoms in space, and this is entropically and energetically favourable effect. It is seen from experimental results that for WAR and W7 the drop of entropy caused by solvation of ions dominates, so that their ΔS° is negative, whereas for W10 the loss of the double hydrogen bridge may be able to neutralize this effect, i.e. ΔS° is close to zero. Due to this compensation of two opposite entropic effects, the contribution of ΔS° to dissociation free energy is relatively little as compared to ΔH° for all three compounds.

3.4 Changes in solvent composition

At the next step we have performed additional experiments using the same working concentrations of WAR and W10 (0.2 mg mL⁻¹ in the injected samples), and the media containing 10 mM sodium dodecyl sulfate (SDS) and 15% (v/v) acetonitrile (ACN), i.e. the micellar and aprotic cosolvent systems. It was dictated by an interesting idea to investigate the changes in enthalpy–entropy relations, and the corresponding pK_a shifts, upon introduction of two different solvent modifiers. Micelles formed by SDS constitute a hydrophobic pseudostationary phase and a potential platform for hydrophobic interactions with non-polar species. ACN, in turn, is a polar aprotic solvent prone to rearrangement of non-covalent electrostatic interactions in the solvent.

The values of pK_a shifts and related ΔH° and ΔS° parameters have been shown in Table 2. It is noticeable that addition of SDS increases pK_a of WAR by around 1.5 pH unit, and W10 by around 0.8 pH unit. These results confirm that interactions with micelles favour the neutral forms of both molecules, leading to the shifts in dynamic equilibrium. Deeper insight into this matter is provided by the obtained plots of electrophoretic mobility versus pH, presented in Fig. 6. We see that growing pH entails a decline of absolute mobility of both molecules. Remarkably, the plots are characterized by sigmoidal shape and inflection points, whose values are very close to pK_a values revealed by DAD method. These outcomes indicate that deprotonation must bring about exclusion of molecules from micellar environment and their transfer to aqueous solvent. The two related factors contribute to this: rise of polarity which hiders intermolecular interactions of non-polar residues, and appearance of negative charge which is repelled by negatively charged heads of surfactants molecules. It is visible as a decrease in mobility, since the micelles are repeatedly ionized due to numerous sulfate groups and thereby more mobile than the singly ionized molecules of WAR and W10. Very consistent picture of events may be delineated based on ΔH° and ΔS° values obtained in this system, see Table 2.

Table 2 The values of thermodynamic parameters determined experimentally for WAR and W10 in the modified media^a

Compound	Modifier	pKa (pKa shift)	ΔH° (kJ mol^−1)	ΔS° (J mol^−1 K^−1)
a The pKa values refer to temperature of 293 K.
WAR	SDS	6.39 (+1.44)	14.6	−8.7
	ACN	5.38 (+0.43)	2.04	−4.0
	Reference	4.95	16.9	−4.4
W10	SDS	6.89 (+0.77)	13.8	−10.2
	ACN	6.32 (+0.20)	8.4	−11.1
	Reference	6.12	34.3	0.0

---

Fig. 6 The relation between μ_eff values and pH obtained for WAR (A) and W10 (B) at 293 K in the micellar system containing 10 mM SDS.

One can see that for both WAR and W10 a drop of ΔH° and ΔS° values is observed as compared with reference aqueous medium. Exclusion of molecules from micelles upon deprotonation leads unarguably to creation of new hydration shells around anionic forms, and possibly, to intermolecular interactions with water dipoles. By contrast, the neutral forms embedded in micelles may be prevented from such interactions. In this reasoning the changes in ΔS° derives from organization of water molecules around ionized species liberated from micelles, and this is consistent with general description of a “hydrophobic effect”, often cited in literature (note that in aqueous medium the non-dissociated forms are better solvated than inside micelles).¹¹ Interpretation of ΔH° is however not straightforward and impeded by a multitude of possible factors that may account for alterations in heat capacity, e.g. one should consider an unknown structure of micellar complexes. Interestingly, the apparent pK_a shifts that arise from these interactions are fairly large, up to 1.5 pH unit for WAR. Another striking observation is that in the micellar system WAR and W10 become quite similar in ΔH° and ΔS° values. The most likely explanation of this effect is a loss of the specific intramolecular bonding by W10, and concomitantly, a loss of the only distinctive feature responsible for specific thermodynamics of W10 in aqueous medium. One may conjecture that OH⋯OH⋯O linkage is vulnerable to any distortions in nearby environment, and it may be broken during integration with micelles. Deeper investigation of this effect is however beyond the scope of the present work.

It is seen from Table 2, in contrast to SDS, that for WAR ACN affects only the ΔH° values while ΔS° remains almost unchanged. ACN is a polar molecule and thereby does not form the analogous non-polar microenvironment, and consequently, does not participate in hydrophobic effect. Instead, aprotic ACN molecules are known to rearrange network of water dipoles and change hydrogen donor–acceptor abilities of solvent. This specific impact on solvent properties is presumable reason for why only enthalpic term, usually referred to formation/breaking of bonds, changes significantly in this system. Analogously to the micellar system, the differences between WAR and W10 are also considerably smaller than in the reference aqueous system. It implies that the specific double intramolecular hydrogen bridge OH⋯OH⋯O may also be lost in the presence of ACN molecules. In consequence, this bonding seems to be strictly solvent-dependent.

One should emphasize that these results constitute only an approximate insight into the effects encountered during changes in solvent composition, and they are burdened with some uncertainty. In particular, the effect related to changes in dielectric permittivity along with increase in temperature for different systems (aqueous, micellar and cosolvent) has not been recognized. One should however note that such effect may influence accuracy of the thermodynamic terms determined from the van't Hoff model.^41–43 In addition, pK_a values have been determined as “apparent” parameter valid only for the given solvent composition, i.e. 10 mM SDS and 15% ACN. In the case of SDS the observed shifts of pK_a may be strictly dependent on binding degree, which for W10 could be lower due to the presence of additional OH group. In fact, some difference is visible from Fig. 6, where WAR exerts larger absolute mobility than W10 in the non-ionized state during interaction with SDS molecules. Deeper investigation of these issues is not obligatory for the main idea of this work, but appears to be an interesting direction of the future research.

Considering these all facts together, one can however state that the micellar and aprotic cosolvent systems are the elegant reference for aqueous medium. They explicitly show that enthalpic and entropic effects are independent thermodynamic forces and their interrelations observed in experiment may disclose nature of events occurring on a molecular level.

4 Concluding remarks

In the present study the thermodynamic contributions (ΔH°, ΔS°) to free dissociation energy of warfarin (WAR), 7-hydroxywarfarin (W7) and 10-hydroxywarfarin (W10) in water solvent have been for the first time studied experimentally and computationally. In addition, the system containing sodium dodecyl sulfate (SDS) and acetonitrile (ACN) cosolvent have been studied. As far as ΔH° is concerned, it has been found that among these structurally similar molecules W10 exhibits distinctively the highest positive enthalpy of deprotonation (+34.3 kJ mol⁻¹), whereas the similar values have been obtained for WAR and W7 (+16.9 kJ mol⁻¹ and +18.4 kJ mol⁻¹, respectively). The entropic term has appeared to be similarly negative for WAR and W7 (−4.4 J mol⁻¹ K⁻¹, and −4.2 J mol⁻¹ K⁻¹, respectively), whereas it is nearly zero for W10. It has been suggested that one of the factors that determine acid–base properties of WAR and its hydroxylated derivatives in water medium is the presence of intramolecular hydrogen bonds involving the ionizable hydroxyl group. The double linear linkage OH⋯OH⋯O noted for W10 seems to be of a paramount relevance for direction and magnitude of enthalpic and entropic effects that accompany dissociation of proton. Most likely, it increases spatial organization of molecule and constricts its flexibility, more significantly that the single OH⋯O bond observed for WAR. Higher stability of the non-dissociated W10 form, in comparison to WAR, derives from energetically unfavourable gain of enthalpy during dissociation, that reflects disconnection of the long intramolecular bridge. This effect is, however, partially counterbalanced by entropic factors that favour dissociation of W10 as compared with WAR. Therefore, a compensatory enthalpy–entropy relationship is observed. These interpretations are supported by the observation that W7, which forms only the single OH⋯O bond, behaves similarly to WAR, despite possessing the second hydroxyl group. Modification of the solvent composition by addition of surfactant (SDS) or polar aprotic cosolvent (ACN), alters dissociation thermodynamics, and shifts pK_a values in upward direction. The nature of effects standing behind these two modified systems is, however, totally different. In the micellar system the entropic factors become a dominant force and they dictate direction and magnitude of pK_a shifts. They correspond evidently to a transfer of the dissociated species from micelles to aqueous environment. In the aprotic cosolvent system, most likely, changes in hydrogen donor–acceptor properties of solvent are reflected by enthalpic term, with a marginal significance of entropic factors.

Acknowledgements

Paweł Nowak has received financial support from Krakowskie Konsorcjum “Materia-Energia-Przyszłość” within the subsidy KNOW. The research was carried out with equipment purchased with financial support from the European Regional Development Fund within the framework of the Polish Innovation Economy Operational Program (contract no. POIG.0 2.01.00-12-0 23/08). The authors gratefully acknowledge the Ministry of Science and Higher Education for financial support (P. Nowak, Iuventus Plus 2015–2017, grant no. IP2015 033273). We are also grateful to Academic Computer Center CYFRONET (PL-Grid Infrastructure) for the computer time.

Notes and references

1. S. Babić, A. J. M. Horvat, D. Mutavdžić-Pavlović and M. Kaštelan-Macan, Trends Anal. Chem., 2007, 26, 1043–1061.
2. I. Ghosh and W. M. Nau, Adv. Drug Delivery Rev., 2012, 64, 764–783.
3. A. C. Bhasikuttan, H. Pal and J. Mohanty, Chem. Commun., 2011, 47, 9959–9971.
4. N. Saleh, A. L. Konerand and W. M. Nau, Angew. Chem., Int. Ed., 2008, 47, 5398–5401.
5. N. Saleh, M. A. Meetani, L. Al-Kaabi, I. Ghosh and W. M. Nau, Supramol. Chem., 2011, 23, 654–661.
6. C. Klock, R. N. Dsouza and W. M. Nau, Org. Lett., 2009, 11, 2595–2598.
7. M. D. Pluth, R. G. Bergman and K. N. Raymond, Science, 2007, 316, 85–88.
8. P. Nowak, M. Garnysz, M. P. Mitoraj, F. Sagan, M. Woźniakiewicz and P. Kościelniak, J. Chromatogr. A, 2015, 1377, 106–113.
9. A. M. Rizzi and L. Kremser, Electrophoresis, 1999, 20, 2715–2722.
10. M. Shaikh, Y. M. Swamy and H. Pal, J. Photochem. Photobiol., A, 2013, 258, 41–50.
11. F. Biedermann, W. M. Nau and H. J. Schneider, Angew. Chem., Int. Ed., 2014, 53, 11158–11171.
12. N. Barooah, J. Mohanty, H. Pal and A. C. Bhasikuttan, J. Phys. Chem. B, 2012, 116, 3683–3689.
13. V. Khorwal, B. Sadhu, A. Dey, M. Sundararajan and A. Datta, J. Phys. Chem. B, 2013, 117, 8603–8610.
14. N. Barooah, M. Sundararajan, J. Mohanty and A. C. Bhasikuttan, J. Phys. Chem. B, 2014, 118, 7136–7146.
15. L. S. Kaminsky and Z.-Y. Zhang, Pharmacol. Ther., 1997, 73, 67–74.
16. M. Gebauer, Bioorg. Med. Chem., 2007, 15, 2414–2420.
17. P. Nowak, P. Olechowska, M. Mitoraj, M. Woźniakiewicz and P. Kościelniak, J. Pharm. Biomed. Anal., 2015, 112, 89–97.
18. J. R. Rush, S. L. Sandstrom, J. Yang, R. Davis, O. Prakash and P. W. Baures, Org. Lett., 2005, 7, 135–138.
19. D. Kanamori, A. Furukawa, T. Okamura, H. Yamamoto and N. Ueyama, Org. Biomol. Chem., 2005, 3, 1453–1459.
20. L. Mammino and M. M. Kabanda, J. Phys. Chem. A, 2009, 113, 15064–15077.
21. M. M. Deshmukh, L. J. Bartolotti and S. R. Gadre, J. Comput. Chem., 2011, 32, 2996–3004.
22. G. Wenz, Beilstein J. Org. Chem., 2012, 8, 1890–1895.
23. E. Nazarparvar, M. Zahediand and E. Klein, J. Org. Chem., 2012, 77, 10093–10104.
24. P. Durlak and Z. Latajka, Phys. Chem. Chem. Phys., 2014, 16, 23026–23037.
25. A. S. Vlasenko, L. P. Loginova and E. L. Iwashchenko, J. Mol. Liq., 2009, 145, 182–187.
26. Z. Yuanqin, L. Fan, L. Xiaoyan and L. Jing, Talanta, 2002, 56, 705–710.
27. P. Nowak, M. Woźniakiewicz and P. Kościelniak, J. Chromatogr. A, 2015, 1377, 1–12.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian Inc., Wallingford CT, 2009.
29. W. Gao, H. Feng, X. Xuan and L. Chen, J. Mol. Model., 2012, 18, 4577–4589.
30. Y. Cho, S. K. Min, J. Yun, W. Y. Kim, A. Tkatchenko and K. S. Kim, J. Chem. Theory Comput., 2013, 9, 2090–2096.
31. J. Hoand and M. L. Coote, Theor. Chem. Acc., 2010, 125, 3–21.
32. CPMD, http://www.cpmd.org/, Copyright IBM Corp 1990–2015, Copyright MPI für Festkörperforschung Stuttgart 1997–2001.
33. R. W. Hockney, Methods Comput. Phys., 1970, 9, 136–210.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. C. Hartwigsen, S. Goedecker and J. K. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662.
36. R. W. Hockney, Methods Comput. Phys., 1970, 9, 136–210.
37. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
38. (a) M. Gupta, E. F. da Silva and H. F. Svendsen, J. Phys. Chem. B, 2012, 116, 1865–1875; (b) M. Gupta, E. F. da Silva and H. F. Svendsen, J. Phys. Chem. B, 2013, 117, 7695–7709.
39. A. Mishra, S. K. Srivastava and D. Swati, Spectrochim. Acta, Part A, 2013, 113, 439–446.
40. E. L. Regalado, E. C. Sherer, M. D. Green, D. W. Henderson, R. T. Williamson, L. A. Yoyce and C. J. Welch, Chirality, 2014, 26, 95–101.
41. Y. Y. Fialkov, V. Y. Gorbachev and T. A. Kamenskaya, J. Mol. Liq., 2003, 102, 277–284.
42. Y. Y. Fialkov and S. I. Rudneva, J. Mol. Liq., 2002, 100, 59–64.
43. Y. Y. Fialkov, V. Y. Gorbachev and T. A. Kamenskaya, J. Mol. Liq., 2000, 89, 159–167.

---

Footnote

† Electronic supplementary information (ESI) available: The calculated dissociation (deprotonation) enthalpies and entropies. The Hirshfeld atomic charges and the electrostatic potentials of WAR and W10. See DOI: 10.1039/c5ra11623f

---