Dielectric hysteresis behaviors of polyvinylidene fluoride-based multilayer dielectrics controlled by confined distribution of conductive particles†
Jiaming Zhua,
Shanshan Luoa,
Bo Caob,
Jiabin Shen*a and
Shaoyun Guo*a
aState Key Laboratory of Polymer Materials Engineering, Polymer Research Institute of Sichuan University, Chengdu 610065, P. R. China. E-mail: shenjb@scu.edu.cn; nic7702@scu.edu.cn; Fax: +86-28-85466255; Tel: +86-28-85466077
bDepartment of Materials Science & Engineering, University of Washington, Seattle, Washington 98195, USA
First published on 28th July 2015
Abstract
Polyvinylidene fluoride (PVDF)-based multilayer dielectrics containing alternating layers of carbon black (CB) were fabricated through layer-multiplying extrusion. Benefits from the presence of PVDF between CB-containing layers, the breakdown strength and hysteresis behaviors of the multilayer specimens were investigated. The multilayered distribution of conductive particles was considered to be preferred for controlling the energy conversion and storage of dielectric materials.
The continued prosperity of micro-electronic industries and portable smart devices creates demand for high performance polymer based dielectric capacitors.1–7 Currently, with the pursuit of reduced size, weight, cost, improved security and stability in advanced electronic devices, future applications of materials in these newborn devices impose great challenges to polymer/conductive particles dielectric (PCD) composites. Despite the high dielectric permittivity of the PCD composite that is anticipated in terms of the Maxwell–Wagner–Sillars interfacial polarization,8 the enormous loss and ultra-low breakdown strength have limited its applications, for instance, dielectric hysteresis behavior, which is considered as a dominant factor in achieving high performance energy materials.9 Based on the fundamental knowledge of the D–E hysteresis theory, the energy density derived from the following equation is one of crucial parameters in evaluating the energy storage of dielectric materials.
 | (1) |
Amounts of approaches have been developed to enhance the breakdown strength by reducing or even cutting off the direct contact of conductive components along the electric field direction. Surficial modification and completely encapsulation on conductive particles have been demonstrated as effective methods, the core–shell like morphology would barrier the direct touch of neighboring conductive components. Grafting polar groups on the particle surface and natural oxidation were both identified to be useful for preventing the undesired conductance as they provide the mediate barrier components, resulting in low dielectric loss.10,11 Shen et al.12 encapsulated silver particles with an organic carbonaceous shell, achieving a higher permittivity, lower loss and much higher breakdown strength than pristine composites. In addition, three phase strategies with synergistic effect of ceramic and conductive particles were widely performed by Dang and Luo et al.13–16 to reduce the percolation threshold and enhance anti-breakdown behavior. Though outstanding progress has been made on the conventional PCD composites, the final performances are still sensitive to filler loadings, causing a great difficulty in controlling the hysteresis behaviors.
Recently, Liu et al. demonstrated that the anisotropic alignment of particles in polymer matrix would have an excellent dielectric behavior benefited from the existence of barrier polymer phase.17 The highly oriented CNTs in polymer matrix enable a multilayer capacitor-like structure, resulting in a considerable high breakdown strength and energy density. Inspired by the anisotropic alignment strategy, layer-multiplying coextrusion technology was applied to fabricate a series of multilayered PCD composites consisting of alternating neat polymer (NP) layers and polymer/conductive filler composite (PF) layers in our recent published work.18,19 Due to the separation of insulated NP layers, conductive fillers can be effectively distributed in confined layer spaces forming an anisotropic alignment of conductive pathways. The alternating assembly of insulated and conductive layers can be regarded as a multilayer capacitor-like structure. It has been revealed that the dielectric permittivity can be controlled by changing the distance between two adjacent conductive layers which are determined by the number of layers at a given thickness.18 However, the dielectric hysteresis behaviors and potential applications in energy storage were less reported before.
In this work, the polymer material was polyvinylidene fluoride (PVDF), while carbon black (CB) particles were chosen as conductive fillers instead of other high aspect ratio ones with a higher conductivity (such as CNTs, graphene, metal fibers, etc.) to avoid the influence of the layer-multiplying process on the orientation of fillers. Conductive CB particles (15 wt%) were firstly mixed with PVDF and melt extruded from a twin-screw extruder forming PVDF/CB pellets (denotes as cPVDF), then the dried cPVDF and neat PVDF pellets were coextruded from the layer-multiplying equipment forming 4-, 16- and 64-layer PVDF/cPVDF materials. The microstructure of each specimen was examined through polarized optical microscope (POM). As shown in Fig. 1(a)–(c), numerous interfaces can be observed between bright and dark layers (corresponding to PVDF and cPVDF layers, respectively) indicating that well-defined alternating distribution of conductive particles was obtained. With increasing the number of layers, the thickness of each layer reduces proportionally while the total thickness of each specimen maintains at 1 mm (more detail processes of sample preparation and characterization are described in the ESI†).
 | ||
| Fig. 1 (a–c) POM images of 4-, 16- and 64-layer PVDF/cPVDF specimens; (d) dielectric permittivity and loss factor of PVDF/cPVDF multilayer dielectrics and neat PVDF as a function of frequency. | ||
For linear dielectrics, such as polymers or polymer composites, the eqn (1) can be simplified as follow:9
 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) of the multilayer specimens is controlled at a low level by increasing the number of layers. The maximum magnitude of 64-layer specimen is lower than 0.3 at 106 Hz, still comparable to pure PVDF.
δ) of the multilayer specimens is controlled at a low level by increasing the number of layers. The maximum magnitude of 64-layer specimen is lower than 0.3 at 106 Hz, still comparable to pure PVDF.
Based on the Series model of parallel-plate capacitors in a static electric field,20 the εr of a PVDF/cPVDF multilayer dielectrics can be obtained as follow,
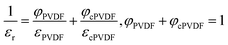 | (3) |
Although the dielectric permittivity of multilayer dielectrics shows a promising result, the breakdown strength of PCD system is even more important for energy applications according to eqn (2). In most of conventional PCD systems, the controllable electric hysteresis behavior cannot be observed due to its extremely low breakdown strength. However, as the conductive particles are distributed in the alternating confined layer spaces, the leakage current along the direction of electric field would be inhibited. In this work, the breakdown strengths of 64-layer PVDF/cPVDF specimen and the PVDF/CB conventional composite with a similar dc conductivity were measured at the same condition, respectively. Results demonstrate that benefited from the separation of well-defined insulated PVDF layers, the breakdown strength of the multilayer specimen reaches about 9 MV m−1, much higher than that of conventional one, 0.04 MV m−1. Fig. 2(a) displays the surface of 64-layer specimen as the applied voltage reaches breakdown point and a cavity can be observed under an optical microscope. It is known that when an exorbitant voltage is applied on a resistor, a large extent of exothermic process would be generated. Hence, as the conductive cPVDF layers are combined with insulated PVDF layers cutting off the conductive pathways along the direction of electric field, the temperature would abnormally rise up accompanied with increasing the applied voltage, leading to the melting and catastrophic deformation of the whole material as shown in the magnified image of Fig. 2(b).
 | ||
| Fig. 2 (a) Surface image of 64-layer PVDF/cPVDF specimen after the breakdown test, (b) is the magnified image. | ||
Despite extremely high permittivity can be obtained from percolative PCD composite, the over-low breakdown strength may barrier its electric displacement behavior. Thus, few reports have been put forward to illustrate the electric hysteresis behavior of PCD systems. Differently, above results reveal that the multilayer dielectrics consisting of neat polymeric insulated layers and conductive particle-filled conductive layers provide a convenient route to control the breakdown strength by changing the number of layers, so that the electric hysteresis behaviors may be observed under a moderate electric field. Fig. 3(a) shows the D–E hysteresis loops of neat PVDF and PVDF/cPVDF multilayer dielectrics. It is worth noting that the 4-layer specimen exhibits an almost linear hysteresis behavior corresponding to large energy conversion efficiency, meanwhile its electric displacement is much higher than that of neat PVDF. This indicates that the material with a multilayered assembly may have promising applications in energy field if the linear hysteresis behavior can be maintained. However, the hysteresis loop opens up and shows a non-linear ferroelectric-like behavior accompanied with increasing the number of layers, though the electric displacement enhances gradually. The increased energy dissipation occurring in the polarization process is consistent with the tendency of the loss factor measured through impedance analyzer as shown in Fig. 1(d), which is ascribed to the movement of electric charges induced by the interfacial polarization. Furthermore, Fig. 3(b) displays the released energy density (Ed) of neat PVDF and multilayer specimens. Compared with that of neat PVDF, the Ed of 4-layer specimen rises up much faster with increasing the field strength. As the electric field reaches 8 kV cm−1, the Ed approaches to about 0.12 mJ cm−3, three times larger than that of neat PVDF, which reveals that more energy would be stored in the multilayer dielectric. However, owning to the large energy loss, the Ed of 16- and 64-layer specimens are increased limitedly, though high electric displacement is possessed. Thus, an appropriate layer number would be preferred for attaining a large Ed and high energy conversion efficiency.
In summary, the alternating assembly of neat PVDF layers and CB-filled PVDF layers promotes the accumulation of electric charges at the layer interfaces leading to a distinct increase of dielectric permittivity due to the occurrence of interfacial polarization. However, benefit from the presence of PVDF between the CB-containing layers, only slight enhancement in dielectric loss occurs and the breakdown strength of 64-layer specimen is at least two orders of magnitude higher than that of PVDF/CB conventional composite at a similar conductivity level. Thus, the electric hysteresis behaviors are observed under a moderate electric field. With increasing the number of layers, the hysteresis loop tends to open up and the calculated release energy density rises up gradually. Thus, the confined alternative alignment of conductive particles in polymer matrix can be regarded as a potential route to control the energy conversion and storage of PCD materials.
Acknowledgements
The authors are grateful to the National Natural Science Foundation of China (51203097, 51227802, 51420105004, 51421061) and the State Key Laboratory of Polymer Materials Engineering (sklpme2015-3-03) for financial support of this work. We also appreciate for the help in polarization tests provided by the research group of Prof. Jianguo Zhu.Notes and references
- P. Jain and E. J. Pymaszewski, Thin Film Capacitors for Packaged Electronics, Kluwer, Norwell, MA, 2003 Search PubMed.
- Y. Cao, P. C. Irwin and K. Younsi, IEEE Trans. Dielectr. Electr. Insul., 2004, 11, 797 CrossRef.
- H. S. Nalwa, Handbook of Low and High Dielectric Constant Materials and Their Applications, Academic Press, London, 1999 Search PubMed.
- M. S. Whittingham, MRS Bull., 2008, 33, 411 CrossRef CAS.
- P. Simon and Y. Gogotsi, Nat. Mater., 2008, 7, 845 CrossRef CAS PubMed.
- B. Neese, B. Chu, S. G. Lu, Y. Wang, E. Furman and Q. M. Zhang, Science, 2008, 321, 821 CrossRef CAS PubMed.
- B. Chu, X. Zhou, K. Ren, B. Neese, M. Lin, Q. Wang, F. Bauer and Q. M. Zhang, Science, 2006, 313, 334 CrossRef CAS PubMed.
- C. W. Nan, Y. Shen and J. Ma, Annu. Rev. Mater. Res., 2010, 40, 131 CrossRef CAS.
- Z. M. Dang, J. K. Yuan, S. H. Yao and R. J. Liao, Adv. Mater., 2013, 25, 6334 CrossRef CAS PubMed.
- R. R. Kohlmeyer, A. Javadi, A. Pradhan, S. Pilla, K. Setyowati, J. Chen and S. Q. Gong, J. Phys. Chem. C, 2009, 113, 17626 CAS.
- A. B. Da Silva, M. Arjmand, U. Sundararaj and R. E. S. Bretas, Polymer, 2014, 55, 226 CrossRef PubMed.
- Y. Shen, Y. Lin, M. Li and C. W. Nan, Adv. Mater., 2007, 19, 1418 CrossRef CAS PubMed.
- Z. M. Dang, Y. Shen and C. W. Nan, Appl. Phys. Lett., 2002, 81, 4814 CrossRef CAS PubMed.
- Z. M. Dang, S. H. Yao, J. K. Yuan and J. Bai, J. Phys. Chem. C, 2010, 114, 13204 CAS.
- Z. M. Dang, B. Xia, S. H. Yao, M. J. Jiang, H. T. Song, L. Q. Zhang and D. Xie, Appl. Phys. Lett., 2009, 94, 042902 CrossRef PubMed.
- S. Luo, S. Yu, R. Sun and C. P. Wong, ACS Appl. Mater. Interfaces, 2014, 6, 176 CAS.
- H. Liu, Y. Shen, Y. Song, C. W. Nan, Y. Lin and X. Yang, Adv. Mater., 2011, 23, 5104 CrossRef CAS PubMed.
- J. M. Zhu, J. B. Shen, S. Y. Guo and H.-J. Sue, Carbon, 2015, 84, 355 CrossRef CAS PubMed.
- W. L. Gao, Y. Zheng, J. B. Shen and S. Y. Guo, ACS Appl. Mater. Interfaces, 2015, 7, 1541 CAS.
- Z. M. Dang, J. K. Yuan, J. W. Zha, T. Zhou, S. T. Li and G. H. Hu, Prog. Mater. Sci., 2012, 57, 660 CrossRef CAS PubMed.
- R. Ravi, P. Kamaraj and R. Ranganathan, Interactive Physics,MTG Learning Media, Noida, India, 2011 Search PubMed.
- A. K. Jonscher, Dielectric Relaxation in Solids, Chelsea Dielectric Press Limited, London, 1983 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra11596e |
| This journal is © The Royal Society of Chemistry 2015 |

