Chemisorbed oxygen atom on the activation of C–H bond in methane: a Rh model study†
Abstract
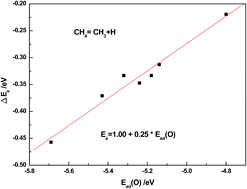
Single atom catalysts usually show unique catalytic activity and the physical nature is not clear. In the present work, density functional theory calculations are presented for adsorption and dissociation of CH4 on clean and oxygen atom pre-adsorbed Rh metal surfaces with different coordinate numbers such as (111), (100), (110), (211), kink, ad-row (add two atoms on a p(2 × 2)-111 unit cell) and ad-atom (add one atom on a p(2 × 2)-111 unit cell). The present calculation results show that the pre-adsorbed oxygen atom inhibits the methane dehydrogenation on Rh surfaces in general except on the ad-atom model where it has no effect, thus resulting in the possibility of the partial oxidation of methane to produce syngas (the mixture of CO and H2) on Rh ad-atom catalysts. Having been analyzed by the barrier decomposition method, it was found that the presence of an oxygen atom usually reduces the adsorption energy of dissociated fragments and increases the interaction between the dissociated fragments, both of which lead to an increase of the reaction barrier. Moreover, the electronic analysis indicated that the oxygen effect can be attributed to the strong interaction of acid–base pair sites on oxygen–metal systems, and a strong acid–base interaction related to the low dehydrogenation barrier.

 Please wait while we load your content...
Please wait while we load your content...