 Open Access Article
Open Access ArticleEffect of dielectric constant on estimation of properties of ionic liquids: an analysis of 1-alkyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide†
Lourdes del
Olmo
,
Isabel
Lage-Estebanez
,
Rafael
López
and
José M.
García de la Vega
*
Departamento de Química Física Aplicada, Facultad de Ciencias, Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: garcia.delavega@uam.es
First published on 19th August 2015
Abstract
A series of different cationic structures based on 1-alkyl-3-methylimidazolium were combined with a single anion, bis(trifluoromethylsulfonyl)imide (CnmimNTf2, n = 1 to 12) for analyzing the quality of COSMO-RS based estimations. For this purpose, we have studied the structure as well as the estimations of several properties of one ionic liquid (IL). These estimations are obtained from polarization charge distribution in which the IL is embedded. Special attention has been paid to the effect of the dielectric constant value in the predictions. For this purpose, polarization charge density has been modeled using several values of dielectric constant, and properties have been estimated in each case. Thus, σ-profiles and, σ-potentials have been computed and used with COSMO-RS for estimating vapor pressure, as a function of temperature, as well as theoretical values of vaporization enthalpy, density, and viscosity at 298.15 K. The influence of the length of the alkyl chain of ionic liquid in the estimation of these properties has also been tested. Finally, the results have been compared with experimental data.
1 Introduction
Ionic liquids (ILs) are molten salts composed of bulky and asymmetric organic cations and organic or inorganic anions. These bulky ions have disperse charges and low lattice energies, lowering, thereby, the IL melting temperature and allowing them to be in the liquid state at or near room temperature.1,2 They are being evaluated as potential alternative solvents in practical applications due to their low volatility, high solvent capacity, and high chemical and thermal stability. ILs offer several advantages when used as solvents, due to the possible regeneration and reutilization, the reduction of energy consumption, and lower costs associated with several processes. In particular, ILs are being investigated in a wide diversity of fields involving chemistry,3–5 biochemistry,6–8 electrochemistry,9–11 engineering,12–15 and material science,16–18 and are being examined as possible solvents for different captures.19–21 In particular, solubility of carbon dioxide in ILs is an active field of research, which includes both experimental work,22–25 and theoretical search using molecular dynamics simulations.26,27However, in order to be useful as solvents, these favorable features must overcome the less favorable transport properties, related to their high viscosity and surface tension. Thus the choice of a particular IL for a given application requires the improvement of several design parameters. This fact can become a cumbersome process due to the huge number of possible combinations between ions. The combination of cation–anion pairs28,29 and the molecular structure of the ions30,31 affect to the properties of ILs, and therefore must be considered in the selection process. Furthermore, specific structural aspects as the length of alkyl chain substituents32,33 can be used for tuning ILs for specific purposes. Because of this, ILs have been termed designer solvents.34–36
In order to facilitate a first selection, theoretical methods can be useful since they are usually faster and cheaper than experimental procedures. Process simulation is one of such methods, which proves to be a powerful tool to make predictions on the performance of systems in the equipment environment.37,38 However, this simulation needs information about different thermochemical properties of the IL such as enthalpy, melting and boiling points, density and viscosity. Some of them are difficult to measure (even impossible in some cases like with normal boiling temperatures). In these cases, reliable theoretical estimations could be used as input to the simulator.
Computational methods provide a possible alternative in terms of means for quantitative theoretical predictions of thermochemical properties. Given the nature of the problem, methods based on quantum treatments may be preferable, but most of them have been devised to deal with single molecules or clusters of relatively few molecules. This is insufficient for a good description of liquid phases. However, at the end of the last century, an appealing method was proposed for estimating these properties in liquid phase, namely, the COnductor-like Screening MOdel for Real Solvents (COSMO-RS).39 This method combines quantum calculations of the molecular structure on single molecules, with a cavity model to simulate the effects of environment, followed by an original a statistical treatment.
In COSMO40 model (the starting point of COSMO-RS treatment), the effect of environment on a given molecule is simulated in terms of a polarization charge density located on the surface of a cavity surrounding the molecule. The cavity is built by a superposition of spheres centered at the nuclei of the molecule with radii which usually are taken as 1.2 times their van der Waals radii. The charge density is determined with the condition that the total electric field (or, alternatively, its electrostatic potential) vanishes over the cavity surface.41
When applying COSMO-RS, it is customary to take the polarization charge density corresponding to a molecule whose electron density corresponds to the molecule placed in vacuum. However, real molecules are embedded in a more or less polarizable medium, and this fact should be taken into account. One way to introduce this effect is to use a Polarizable Continuum Model (PCM),42 with a given value of the dielectric constant, when computing the electric field or electrostatic potential which determine the polarization charge density.
ILs based on imidazolium cations have been proposed as good solvents in separation processes because the aromatic or aliphatic character of the liquid can be tuned by modifying the alkyl chain length.35,36 In this work, COSMO-RS, combined with a Polarizable Continuum Model with different values for the dielectric constant, has been used to estimate several properties on a family of ILs consisting of alkyl imidazolium cations combined with a single anion.
In particular, predictions have been made for vapor pressure as a function of temperature, and vaporization enthalpy, density, and viscosity at 298.15 K. Furthermore, σ-profiles and σ-potentials have been built to predict their chemical behavior, paying special attention to the influence of the length of the alkyl chain of the cation in the predictions. Finally, the results thus obtained have been compared with available experimental data.43–46
2 Methods and computational details
ILs can be represented in two ways in computational analysis: IL can be considered as independent counterions (C + A model) or as ion-pairs (CA model). Given the complexity of the ions, the number of possible stable structures is quite high, and some preliminary selection must be made. In this case, we have taken as a reference the structures derived in a previous conformational study for CnmimCl series IL.32 For C + A model, the analysis consisted of a geometry optimization of the structures of the independent ions. For CA model, the anion was located in the most stable position in each cation previously optimized.Starting with these structures, geometry optimization of the ions or ion pairs has been carried out at the BVP86/TZVP/DGA1 level using Gaussian09 package,47 including the counterpoise method to correct basis set superposition error (BSSE)48 for CA model, and a calculation of frequencies to identify local minima.
The optimized structures have been used as starting point for COSMO, and the polarization charge on the cavity surface has been computed using different values for dielectric constants plus that of gas phase (ε = 1). It has been reported that values of dielectric constant higher than 80 show insignificant variations in properties.49 Thus, we have chosen four values covering a wide range of ε: 2, 10, 33 and 78, which approximately correspond to some common solvents: benzene, dichloroethane, methanol and water, respectively.
Polarization charges thus obtained are used by COSMO to compute the σ-profile, which relates the values of polarization density with surface areas,41 and σ-potential, used to interpret the chemical behavior and to compute thermal-statistical properties50,51 with COSMOtherm program.52 In this case, BP_TZVP_C30_1201 parameterization level has been chosen.
3 Results and discussion
3.1 Models and dielectric constants: influence on molecular structure
The general molecular structures of ions which compose the ILs treated in this work are shown in Fig. 1. Series based on imidazolium cations from 1,3-dimethyimidazolium (C1mim+) to 1-dodecyl-3-methylimidazolium (C12mim+) and bis(trifluoromethylsulfonyl)imide anion (NTf2−) have been analyzed. As mentioned above ILs can be represented by two models: the independent counterions (C + A) model that considers the cation and anion as independent entities, and the ion-pair (CA) model that considers ion pairs as molecules. The representation for both models is plotted in Fig. 2.To illustrate the influence of the dielectric constant in the results, Table 1 collects the values of interaction energy of ion pair, defined as the difference of total electronic energy between models, i.e., ΔEint = Eion pair − (Ecation + Eanion), for the smallest member of the series (C1mimNTf2). As it is expected, this difference largely depends on the value of ε, being lower as medium polarizability increases. In this table, we have also collected the distance between the proton placed between hydrogen nuclei in imidazolium and the nitrogen of NTf2, as a measure of the anion–cation distance. It can be seen that this distance increases as medium polarizability increases when CA model is considered. This behavior is similar for all ILs. Table S1 in ESI† shows that interaction energies and cation–anion distances do not change significantly with the alkyl chain length. C4mimNTf2 has been chosen because it is widely used as solvent. This IL is considered an interesting candidate in processes of carbon dioxide capture due to its high solubility selectivity.25
| ε | ΔEint | d H(C+)–N(A−) |
|---|---|---|
| 1 | −315.6 | 2.07 |
| 2 | −131.0 | 2.26 |
| 10 | −26.0 | 2.46 |
| 33 | −6.2 | 2.54 |
| 78 | −1.5 | 2.57 |
The results obtained with the highest and lowest dielectric constants considered in this work are compared for the twelve ILs in Table S2 of ESI.† Distances between ions computed with ε = 1 are similar for all these ILs, whereas with the highest dielectric constant the difference is ca. 0.30 Å. Interaction energy is more sensitive to the value of dielectric constant. The difference taking the lowest dielectric constant is ca. 10 kJ mol−1, whereas it is only 1 kJ mol−1 with the highest.
We have also studied the σ-profile of the ILs to analyze the differences on the polarization charge distribution with both models, and the effect of the dielectric constant. The increase of the alkyl chain length of the cation affects the neutral region of σ-profile for both models (see Fig. S1–S4 in ESI†) but keeps the regions of large polarization density unchanged. This means that reactivity of these ILs towards nucleophilic or electrophilic reagents does not depend on the chain length. Moreover, nonsignificant differences of the charge density with different values of dielectric constant for C + A model were observed. Fig. 3 shows an example for the smallest ion pair, C1mimNTf2, in which the differences between models with highest and lowest values of the dielectric constant are shown. Peaks corresponding to CA model are less intense than those of C + A model, and cationic and anionic zones are closer to each other for CA model, suggesting less chemical activity than in C + A model.
 | ||
| Fig. 3 σ-profiles of the C1mimNTf2 represented as both models with ε = 1 (black line) and the highest value considered in this work for dielectric constant: ε = 78 (red line). | ||
The σ-potential of the C1mimNTf2 has been analyzed to predict the chemical behavior. The positive values in the region of positive polarization charge, shown in Fig. 4, suggest repulsive behavior with respect to nucleophilic reagents, and the small negative values in the non-hb range, a slight attractive interaction with nonpolar reagents. This behavior seems to be independent of the value of ε, and equal for all ILs. This is illustrated in Fig. S5 (see ESI†) for C1mimNTf2 and C4mimNTf2. In contrast to this, in the region of negative polarization charges, which reflects the behavior against electrophilic reagents, the σ-potential is highly dependent on the dielectric constant, as Fig. 4 illustrates in case of C1mimNTf2.
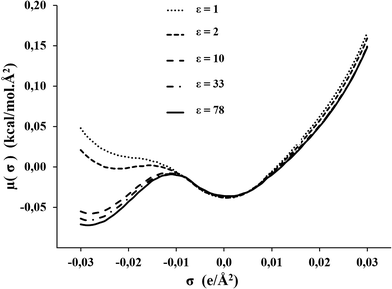 | ||
| Fig. 4 σ-potentials of the C1mimNTf2 modeled as CA model with different values for dielectric constants: 1, 2, 10, 33, and 78. | ||
As a consequence COSMO-RS predictions on the performance of these ILs as solvents of electrophilic reagents will be highly dependent on the value of the dielectric constant chosen in the computation.
3.2 Estimation of properties
 | ||
| Fig. 5 Plot of the vaporization enthalpy trend of CnmimNTf2 (n = 1 to 12) series with ε = 1 and ε = 78 for both models, including experimental data. | ||
 | ||
| Fig. 7 Density for CnmimNTf2 (n = 1 to 12) series with ε = 1 and ε = 78 for both models, including experimental data. | ||
Fig. 7 (see Table S4 in ESI†) shows similar results for the lowest value and the highest value of the dielectric constant. Intermediate values are analyzed in Fig. 8 for C1mimNTf2. For this ion pair, the closest result to experimental data is obtained when considering ionic liquid as C + A model and its polarization charge on surface described with ε = 78. However, it does not differ significantly from the value obtained with ε = 1. The intermediate values of ε give comparable results.
 | ||
| Fig. 8 Density for C1mimNTf2 modeled with different values of dielectric constant, including experimental data in g mL−1. | ||
Experimental measurement of viscosity of ILs is difficult because it usually has very high values at room temperature, and it is very sensitive to the presence of water and other impurities. Viscosities for CnmimNTf2 (n = 1 to 12) series have been estimated using COSMO-RS at 298.15 K (see Table S5 in ESI†). In Fig. 9a, the estimations attained with both models, using different values for dielectric constant, are compared to experimental data.46 A detail of the curves corresponding to ε = 1 (both models), which are closer to experimental data, is depicted in Fig. 9b. Viscosity increases when alkyl chain length of the cation is enlarged. This can be interpreted in terms of higher dispersion forces. Values obtained with ε = 78 are greater than those computed with ε = 1. An intersection of the lines between the CA model and the C + A model corresponding to C8mimNTf2 is clearly visible in Fig. 9b, as well as a second intersection of the lines of CA model and experimental data. Therefore, the best estimations of viscosity are expected using ε = 1, and choosing the model as function of alkyl chain length of cation. CA model is more appropriate for ILs with alkyl chain of n < 8, whereas C + A model is better suited for n > 8.
 | ||
| Fig. 9 (a) Viscosity for CnmimNTf2 (n = 1 to 12) series with ε = 1 and 78, and both models, including experimental data. (b) CA and C + A models with ε = 1, and experimental data. | ||
Finally, we report in Table 2 a summary of results obtained for a particular IL of the series, to give a global view of the effect of models and dielectric constant values in the predictions. For this purpose, we have chosen C4mimNTf2 (experimental ε = 11.6 (ref. 54)). As the Table 2 shows, vaporization enthalpy is underestimated with CA model and overestimated with C + A model. In fact, the best prediction is reached with the highest ε value within CA model. On the contrary, density is better predicted with C + A model, and almost independently of the ε value. Best predictions for viscosity are obtained with low values of ε, almost independently of the model. Here, it is important to notice that the best values of dielectric constant for predicting properties usually do not coincide with the experimental value. This is not so strange as it may appear at a first sight, since in COSMO model ε must be taken as a parameter that can be used to improve the description of the environment local effect over a single ion or ion pair, and which therefore can be different from the bulk average value.
| ε | ΔHvap (kJ mol−1) | ρ (g mL−1) | η (cP) | |||
|---|---|---|---|---|---|---|
| CA | C + A | CA | C + A | CA | C + A | |
| a Data obtained from ref. 45. b Data obtained from ref. 44. c Data obtained from ref. 46. | ||||||
| 1 | 116.0 | 168.5 | 1.419 | 1.438 | 43.58 | 59.07 |
| 2 | 118.4 | 170.1 | 1.399 | 1.442 | 55.44 | 64.35 |
| 10 | 128.3 | 172.0 | 1.403 | 1.440 | 94.42 | 71.88 |
| 33 | 130.3 | 172.6 | 1.404 | 1.440 | 109.44 | 74.19 |
| 78 | 131.8 | 173.1 | 1.399 | 1.439 | 120.30 | 76.49 |
| Experimental | 139.2a | 1.436b | 50.62c | |||
4 Conclusions
The molecular structures for (CnmimNTf2, n = 1 to 12) series designed as two models (CA and C + A) have been computed. Effect of molecular structure and models on estimation of properties has been examined. Different values for dielectric constant have been used to describe the polarization charge on the surface of the cavity. σ-profile and σ-potential of these ILs have been analyzed, and the affinity for hb-donors has been related to increased dielectric constant. Vapor pressure, vaporization enthalpy, density and viscosity have been predicted using COSMO-RS.The size of IL and the dielectric constant affects to the molecular structure of IL. In this work, the size of the IL has been modified increasing the alkyl chain length of the cation, and the polarization charge on the surface of its cavity has been modeled with various dielectric media. Ions described using CA model move away from one another when the values for dielectric constant increase, and the interaction energy decreases.
Negligible vapor pressure is a property which makes ILs interesting. Both models display the same trend as experimental data, CA model being best suited for this property. There is a significant difference in the values of vaporization enthalpies with different values for dielectric constant. CA model seems the most suitable model to estimate these properties.
The influence of alkyl chain length on these properties have also been examined. While density and vapor pressure decrease with the alkyl chain length of the cation, viscosity and vaporization enthalpy increase. Density is greater for C + A model than for CA model. C + A model with the highest dielectric constant (ε = 78) gives results closest to experimental data. On the other hand, viscosity is overestimated for systems larger than C6mimNTf2 with both models.
CA model or C + A model are proposed depending on the property of interest. CA model in gas phase is the most promising model to estimate vapor pressure, vaporization enthalpy and viscosity for CnmimNTf2 (n = 1 to 6) series. C + A model in gas phase is suitable for estimations of density and viscosity for CnmimNTf2 (n = 7 to 12) series.
Acknowledgements
The authors thank the “Ministerio de Ciencia e Innovación” (Project: CTQ2010-19232) and “Comunidad de Madrid” (Project: LIQUORGAS-S2013/MAE-2800) financial support. We also acknowledge CCC-UAM for computational facilities.References
- T. Welton, Chem. Rev., 1999, 99, 2071–2084 CrossRef CAS PubMed.
- V. I. Pârvulescu and C. Hardacre, Chem. Rev., 2007, 107, 2615–2665 CrossRef PubMed.
- R. Marcilla, J. Blazquez, R. Fernandez, H. Grande, J. A. Pomposo and D. Mecerreyes, Macromol. Chem. Phys., 2005, 206, 299–304 CrossRef CAS.
- F. Endres and S. Zein El Abedin, Phys. Chem. Chem. Phys., 2006, 8, 2101–2116 RSC.
- C. I. Daniel, F. Vaca Chávez, G. Feio, C. A. M. Portugal, J. G. Crespo and P. J. Sebastião, J. Phys. Chem. B, 2013, 117, 11877–11884 CrossRef CAS PubMed.
- J. Z. Hao Zhang, J. Wu and J. He, Macromolecules, 2005, 38, 8272–8277 CrossRef.
- A. Brandt, J. Grasvik, J. P. Hallett and T. Welton, Green Chem., 2013, 15, 550–583 RSC.
- D. F. Izquierdo, J. M. Bernal, M. I. Burguete, E. Garcia-Verdugo, P. Lozano and S. V. Luis, RSC Adv., 2013, 3, 13123–13126 RSC.
- A. Deshpande, L. Kariyawasam, P. Dutta and S. Banerjee, J. Phys. Chem. C, 2013, 117, 25343–25351 CAS.
- D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250 CAS.
- S. Maiti, A. Pramanik and S. Mahanty, RSC Adv., 2015, 5, 41617–41626 RSC.
- M. Francisco, A. Arce and A. Soto, Fluid Phase Equilib., 2010, 294, 39–48 CrossRef CAS.
- J. Bedia, E. Ruiz, J. de Riva, V. R. Ferro, J. Palomar and J. J. Rodriguez, AIChE J., 2013, 59, 1648–1656 CrossRef CAS.
- B. Rodríguez-Cabo, A. Soto and A. Arce, J. Chem. Thermodyn., 2013, 57, 248–255 CrossRef.
- R. Gusain and O. P. Khatri, RSC Adv., 2015, 5, 25287–25294 RSC.
- S. Pandey, Anal. Chim. Acta, 2006, 556, 38–45 CrossRef CAS PubMed.
- P. Sun and D. W. Armstrong, Anal. Chim. Acta, 2010, 661, 1–16 CrossRef CAS PubMed.
- T. D. Ho, C. Zhang, L. W. Hantao and J. L. Anderson, Anal. Chem., 2014, 86, 262–285 CrossRef CAS PubMed.
- J. Jacquemin, M. Bendová, Z. Sedláková, M. Blesic, J. D. Holbrey, C. L. Mullan, T. G. A. Youngs, L. Pison, Z. Wagner, K. Aim, M. F. Costa Gomes and C. Hardacre, ChemPhysChem, 2012, 13, 1825–1835 CrossRef CAS PubMed.
- M. Ramdin, S. P. Balaji, J. M. Vicent-Luna, J. J. Gutiérrez-Sevillano, S. Calero, T. W. de Loos and T. J. H. Vlugt, J. Phys. Chem. C, 2014, 118, 23599–23604 CAS.
- Z. Li, Y. Xiao, W. Xue, Q. Yang and C. Zhong, J. Phys. Chem. C, 2015, 119, 3674–3683 CAS.
- S. N. V. K. Aki, B. R. Mellein, E. M. Saurer and J. F. Brennecke, J. Phys. Chem. B, 2004, 108, 20355–20365 CrossRef CAS.
- J. L. Anthony, J. L. Anderson, E. J. Maginn and J. F. Brennecke, J. Phys. Chem. B, 2005, 109, 6366–6374 CrossRef CAS PubMed.
- B.-C. Lee and S. L. Outcalt, J. Chem. Eng. Data, 2006, 51, 892–897 CrossRef CAS.
- I. Bahadur, K. Osman, P. Coquelet, C. Naidoo and D. Ramjugernath, J. Phys. Chem. B, 2015, 119, 1503–1514 CrossRef CAS PubMed.
- M. E. Perez-Blanco and E. J. Maginn, J. Phys. Chem. B, 2010, 114, 11827–11837 CrossRef CAS PubMed.
- M. E. Perez-Blanco and E. J. Maginn, J. Phys. Chem. B, 2011, 115, 10488–10499 CrossRef CAS PubMed.
- C. P. Fredlake, J. M. Crosthwaite, D. G. Hert, S. N. V. K. Aki and J. F. Brennecke, J. Chem. Eng. Data, 2004, 49, 954–964 CrossRef CAS.
- M. Gonzalez-Miquel, J. Bedia, C. Abrusci, J. Palomar and F. Rodriguez, J. Phys. Chem. B, 2013, 117, 3398–3406 CrossRef CAS PubMed.
- L. del Olmo, R. López and J. M. García de la Vega, Int. J. Quantum Chem., 2013, 113, 852–858 CrossRef CAS.
- L. del Olmo, C. Morera-Boado, R. López and J. M. García de la Vega, J. Mol. Model., 2014, 20, 2175 CrossRef PubMed.
- L. del Olmo, I. Lage-Estebanez, R. López and J. M. García de la Vega, J. Mol. Model., 2014, 20, 2392 CrossRef PubMed.
- Z. Huo, L. Tao, L. Wang, J. Zhu, S. Chen, C. Zhang, S. Dai and B. Zhang, Electrochim. Acta, 2015, 168, 313–319 CrossRef CAS.
- M. Freemantle, Chem. Eng. News, 1998, 76, 32–37 Search PubMed.
- A. Arce, M. J. Earle, H. Rodríguez and K. R. Seddon, J. Phys. Chem. B, 2007, 111, 4732–4736 CrossRef CAS PubMed.
- G. W. Meindersma, A. R. Hansmeier and A. B. de Haan, Ind. Eng. Chem. Res., 2010, 49, 7530–7540 CrossRef CAS.
- G. W. Meindersma and A. B. de Haan, Chem. Eng. Res. Des., 2008, 86, 745–752 CrossRef CAS.
- V. R. Ferro, J. de Riva, D. Sanchez, E. Ruiz and J. Palomar, Chem. Eng. Res. Des., 2015, 94, 632–647 CrossRef CAS.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- J. M. S. S. Esperança, Z. P. Visak, N. V. Plechkova, K. R. Seddon, H. J. R. Guedes and L. P. N. Rebelo, J. Chem. Eng. Data, 2006, 51, 2009–2015 CrossRef.
- M. Tariq, P. A. S. Forte, M. F. Costa Gomes, J. N. Canongia Lopes and L. P. N. Rebelo, J. Chem. Thermodyn., 2009, 41, 790–798 CrossRef CAS.
- M. A. A. Rocha, C. F. R. A. C. Lima, L. R. Gomes, B. Schröder, J. A. P. Coutinho, I. M. Marrucho, J. M. S. S. Esperança, L. P. N. Rebelo, K. Shimizu, J. N. Canongia Lopes and L. M. N. B. F. Santos, J. Phys. Chem. B, 2011, 115, 10919–10926 CrossRef CAS PubMed.
- M. Tariq, P. J. Carvalho, J. A. P. Coutinho, I. M. Marrucho, J. N. Canongia Lopes and L. P. N. Rebelo, Fluid Phase Equilib., 2011, 301, 22–32 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- M. Lashkari and M. Arshadi, Chem. Phys., 2004, 299, 131–137 CrossRef CAS.
- A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085 CrossRef CAS.
- A. Klamt and F. Eckert, Fluid Phase Equilib., 2000, 172, 43–72 CrossRef CAS.
- F. Eckert and A. Klamt, COSMOtherm, Version C3.0, Release 12.01, COSMOlogic GmbH & Co.KG, Leverkusen, Germany, 2012 Search PubMed.
- M. A. A. Rocha, F. M. S. Ribeiro, B. Schröder, J. A. P. Coutinho and L. M. N. B. F. Santos, J. Chem. Thermodyn., 2014, 68, 317–321 CrossRef CAS.
- H. Weingärtner, Z. Phys. Chem., 2006, 220, 1395–1405 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra11425j |
| This journal is © The Royal Society of Chemistry 2015 |

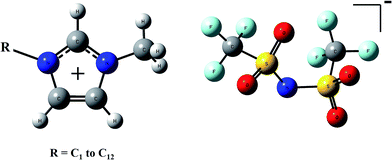

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)