Molecular dynamics simulation of the material removal process and gap phenomenon of nano EDM in deionized water
Xiaoming Yue and
Xiaodong Yang*
Department of Mechanical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China. E-mail: xdyang@hit.edu.cn
First published on 23rd July 2015
Abstract
Nano electrical discharge machining (nano EDM) is a very promising technique to fabricate nanoscale structures on superhard and difficult-to-cut materials, however, the incompleteness and imperfection of the fundamental theory seriously hinders its further application and development. In this paper, a single pulse discharge with nano EDM in deionized water was simulated to study the material ablation process and the bubble dynamic behavior using molecular dynamics. The research results showed that it was not the case that the molten material could not be removed during the discharge duration, instead it was the case that material removal would occur all the time during the whole of the discharge duration, and even after the end of the discharge molten material could still be ablated for a period of time. In addition, it was found that in the early discharge stage, the bubble expansion was impeded by a dielectric liquid, causing an extremely high pressure inside the bubble. It was also found that the expanding bubble and flowing liquid had effects on the removing, carrying, cooling and blocking of the molten and removed material. As a result, the proportion of the removed debris in deionized water was far more than that in gas, while the proportions of spattering material, returning material and bulge material were lower than those in gas, and the range of the volume distribution for the removed debris in deionized water was larger, but the range of the velocity distribution of the removed debris was lower than that in gas. In addition, the bulge generated in gas was much larger and plumper compared to the fragmentary and small bulge generated in deionized water.
1. Introduction
Demands for miniature components are rapidly increasing in the fields of medicine, biotechnology, optics, electronics, and automation, which inspires researchers to explore various kinds of methods and tools to fabricate those nanoscale features using such lithography-based microelectromechanical systems (MEMS) technologies as UV lithography, ion beam lithography (IBL), X-ray lithography, or non-lithography-based technologies such as AFM-based nanometric cutting, nano-imprinting, focused ion beam (FIB), laser based nano-manufacturing technologies and so on. However, when machining nanoscale structures on superhard and difficult-to-cut materials like titanium alloys, the above methods are confronted with the enormous challenges of their restricted choice of machining materials, inability to produce complex geometries, huge capital investment, low machining efficiency or the inevitable cleanroom environment. Nevertheless, it is well known that electrical discharge machining (EDM) is a discharge process in which the thermal energy generated by a pulse discharge between an anode and cathode results in the melting, evaporation and removal of material on electrodes. Thus EDM has exhibited the unique ability to use thermal energy to machine electrically conductive parts, even on nonconductive materials,1,2 regardless of hardness, with high accuracy, and it has become one of the most important methods for manufacturing miniaturized parts.3 But the biggest challenge of this old but novel technique is to develop a fundamental understanding of the material removal process and mechanism. Because EDM occurs in a very short time and randomly within a very narrow space, both theoretical and experimental studies are extremely difficult. Thus, until now, the material removal process and mechanism in EDM has not been fully understood, which has seriously hindered its further application and development.Recent developments in measuring and analyzing instrumentation, such as the high-speed video camera (HSVC), are accelerating new findings and knowledge. For example, A. Kojima et al.4 investigated arc column diameter using a HSVC. M. Kunieda et al.,5 H. P. Schulze et al.6 studied bubble formation with a HSVC. However, those results were influenced by the settings of the HSVC such as exposure time, pixels and aperture, etc. Also, M. Yoshida,7 and J. Wang8 studied the distribution of scattered debris generated in the EDM process. But due to the restriction in the measurement accuracy and the diffuse reflection of light by the bubble, the observation and measurement of the flying debris was limited. Any particles with too small dimensions like nano debris would be inevitably ignored, which would result in incomplete experimental data.
On the other hand, the rapid developments in computer technology and computational mathematics bring new innovation and inspiration to the fundamental research of EDM. In order to find out the evolution process of the bubble and its influence on the material removal mechanism in EDM, many researchers built up simulation models using FEM based on fluid dynamics, and the bubble dynamics behaviors, velocity fields and the pressure distribution in the liquid and bubble were analyzed.9–11 However, in these FEM models, the dynamic behaviors of the bubble and ablating material were not considered simultaneously, which makes it difficult for these models to reveal the influence of the bubble and liquid in essence, such as their effects on the discharge crater and bulge.
Molecular Dynamics (MD) is a useful method to simultaneously analyze the mechanical and thermal behaviors of material at an atomic level by numerically solving the Newton’s equations of motion and has been successfully applied in medical research,12 material research,13 physical and chemical research,14 and even in material machining.15 In recent years, thanks to the technical progresses in EDM, especially that the machining dimension range of EDM can be in the nanometer scale, MD simulations on nano EDM have been made possible in theory and practice. For example, Kunieda et al.16 succeeded in obtaining the submicron crater by using a capacity coupled pulse generator with a discharge duration that was significantly shorter and the diameter of the discharge craters could be as small as 200 nm. Egashira et al.17 successfully achieved holes with a diameter of approximately 500 nm in zinc using silicon electrodes, and they are the smallest diameter holes ever reported for drilling using EDM. Another new technology that can achieve tens of nanometers18–20 has been invented by using equipment like an atomic force microscope (AFM) or a scanning tunneling microscope (STM), with which extremely accurate control of the motion of electrodes can be realized, to give several nanometers between two electrodes. On the basis of the previous pioneering research foundations, Yang21,22 achieved MD simulations of EDM successfully and presented some important results. However, in their models, the discharge gap, assumed as a vacuum for simplicity, differed from that in actual EDM with dielectric liquid, which could not explain the function and influence of the bubble and the dielectric liquid.
Therefore, in this paper, a nano EDM process with a single discharge pulse in deionized water was simulated in order to coincide with reality as far as possible. Based on this simulation model, not only the melting, vaporizing, removing and solidifying processes of the material but also the bubble formation process during a single discharge were visualized and analyzed. Moreover, in order to clarify the influence of the bubble and the dielectric liquid, another MD simulation in which the whole gap was full of gas was also implemented with the same simulation conditions.
2. Simulation model and computational details
2.1 MD model of nano EDM
The simulation was carried out using a large-scale atomic/molecular massively parallel simulator (LAMMPS). Fig. 1 shows the schematic diagram of a nano MD model which consists of an anode, a cathode and a gap. It should be noted that although the gap is full of deionized water during the actual EDM, due to the limitation of computer capacity, the water region was limited to between electrodes, and the other region was simplified as a vacuum, which would be explained in the simulation hypothesis. The gap region was 51 Å thick, 5000 Å wide and long.Fig. 2 shows the sectional view of the simulation model. Both copper electrodes (anode and cathode) were 32a thick, and 60a wide and long (where a is the lattice constant of copper and is equal to 3.61 Å). In order to prevent the electrodes from unexpected movement, boundary atoms were applied on all of the electrode surfaces, except for the working surface where discharge was ignited, and the thickness of the boundary atoms layer was about 2.5a. Also, thermostat atoms were distributed between the boundary atoms and Newtonian atoms to ensure adequate heat conduction in the system, and the thickness of the thermostat atoms layer was about 1.5a. The deionized water area with a density of 0.977 g mL−1 was 51 Å thick, 216.6 Å wide and long and was used as a dielectric liquid. The initial temperatures of the thermostat atom layer, the Newtonian atom layer and the water molecular area were set to be 300 K. The orientations of the monocrystalline copper along the x, y and z axes were [100], [010] and [001], respectively. The discharge was ignited and focused on the Newtonian atom surface near the border with deionized water. In order to analyze the influence of the bubble and the deionized water, another MD simulation in which the electrode model was exactly the same as that in Fig. 2 but that the whole gap was full of gas was also implemented with the same simulation conditions, and because of high computational efficiency, argon gas was used as the gaseous medium in the discharge gap and set to be at 300 K and 0.1 MPa.
2.2 Interaction forces
A three-body Embedded-Atom Method (EAM) potential, which has been extensively used in MD simulations of the interactions between copper atoms, was used in this simulation. For the EAM potential, the total atomic potential energy of system Etot can be expressed using the following equation:
 | (1) |
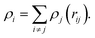 | (2) |
Water molecules were simulated using a rigid SPC water model to describe the inter-molecular interactions like hydrogen bonds and van der Waals interactions. Interactions like the two H–O bonds and the H–O–H angle within a water molecular were held rigidly by the software. Eqn (3) was used to model the hydrogen bond interactions among the water molecules where the charges of the oxygen and hydrogen atoms were −0.820 C and 0.410 C, respectively. The Lennard-Jones potential given in eqn (4) was used to describe the van der Waals interactions among the water molecules. The parameters in the L-J potential were as follows: εO–O = 0.1553 kcal mol−1, σO–O = 3.166 Å.
 | (3) |
 | (4) |
The Lennard-Jones potential given in eqn (4) was also used to govern the non-bonded Cu–H2O interactions, where the hydrogen atoms were not considered due to their negligible role compared to the oxygen atoms. The parameters in the L-J potential were as follows: εCu–O = 0.5983 kcal mol−1, σCu–O = 3.4958 Å.
As for the simulation in argon gas, the Lennard-Jones potential given in eqn (4) was also used to govern the Cu–Ar and Ar–Ar interactions. The parameters in the L-J potential were as follows: εCu–Ar = 1.4979 kcal mol−1, σCu–Ar = 2.872 Å and εAr–Ar = 0.2378 kcal mol−1, σAr–Ar = 3.405 Å.
2.3 Simulation conditions and hypotheses
In the actual EDM process, a series of rapid, repetitive, discrete and randomly distributed sparks are ignited in a short time and in a narrow space, making the simulation model extremely complex and huge. Thus, in order to simplify the analysis process, the following assumptions were adopted without changing the basic characteristics of EDM. Table 1 shows the simulation conditions.| Discharge time (ps) | 4.8 |
| Relaxation time (ps) | 50 |
| Total time (ps) | 124 |
| Discharge power (eV ps−1) | 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 720 720![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
Energy distribution (anode![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cathode cathode![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dielectric liquid) dielectric liquid) |
1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
| Initial radius of discharge column (Å) | 10 |
| Terminative radius of discharge column (Å) | 40 |
| Discharge gap (Å) | 51 |
(1) The discharge column expanded linearly4 and a Gaussian heat source was adopted as the discharge heat source.
(2) It is well known that in actual EDM, a dielectric liquid (like deionized water, kerosene etc.) can dissociate into gases under extremely high temperature, which causes the generation of a bubble, and the gas components and pressure inside this bubble will be different due to the different kinds of dielectric liquid used and the discharge conditions. But the formation process and the influence of the bubble will not change essentially or fundamentally with the variation of the physical properties of the different kinds of gases or the pressure inside the bubble. Thus, in this simulation, the oxygen and hydrogen gases, mainly from the dissociation of water during the actual EDM, were equivalent to the water vapor without hydrogen bonds, due to the fact that up to now MD simulations have been incapable of modelling the dissociation of water molecules on a large scale. Although the physical properties of water vapor are completely different from those of oxygen and hydrogen gases, it is reasonable to analyze the formation process and the influence of the bubble qualitatively. But it should be noted that when the water molecules dissociate into oxygen and hydrogen gas, 2H2O = 2H2 + O2, the molar concentration of gas molecules will increase, and hence the overall gas pressure increases. Thus, when EDM happens in dielectric water, the pressure inside the bubble during the actual EDM can be 1–1.5 times larger than the pressure in this simulation with the same discharge conditions due to the assumption that the dissociation of water is equivalent to the evaporation of water.
(3) During the actual EDM process, the electrode material and the dielectric liquid are evaporated and dissociated in a very short time, resulting in a rapid expansion of the bubble. Since the expansion of the bubble is impeded by the inertia and viscosity of the dielectric liquid, the pressure inside the bubble will be extremely high – i.e. hundreds of megapascals.10 However, limited by the calculation capacity of the computer, the model scale of the dielectric liquid was restricted to between electrodes, and the other regions of the gap were simplified as a vacuum, as shown in Fig. 1. The simulation results in Fig. 4 showed that this simplified model was large enough to simulate the formation and early expansion processes of the bubble and could be used to analyze the early bubble qualitatively. It should be noted that with the expansion of the bubble, the pressure inside the bubble declined accordingly and the simplified model would cause a large deviation when the pressure inside the bubble declined to a certain extent. Thus this simplified model could not be used to analyze the later expansion and contraction processes of the bubble, which needs a much larger scale model of the water in the gap.
(4) Xia et al. performed in depth research on the energy distribution among the anode, cathode and dielectric liquid. The research result23 was about the relationship between the energy distribution ratio and the pulse duration and showed that the energy distribution to the anode and cathode was about 40% and 25%, respectively. Furthermore, when the pulse duration was shorter, the energy distribution approximated to 1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 which was adopted as the energy distribution ratio in this simulation.
1 which was adopted as the energy distribution ratio in this simulation.
(5) In a metal material, it is not only lattice vibration, but also free electrons that make contributions to heat conduction. However, conventional MD theory can only consider the heat conduction caused by lattice vibration, and although many researchers have attempted to modify MD theory to compensate for the influence of free electrons, theoretically acceptable methods have yet to be developed.21 Therefore in this simulation, the influence of the free electrons on heat conduction was neglected and only the lattice vibration was taken into account, which would inevitably bring about some inconsistency with the actual situation. But the simulation results indeed provided some useful explanations for the further understanding of the material removal process and bubble formation process which could be verified experimentally.
3. Material removal and the bubble formation process
After the discharge was ignited, part of the dielectric liquid was evaporated and became a massive gas in a very short time, resulting in the formation of a bubble, which was approximately represented with the dotted lines in Fig. 3. Since the expansion of the bubble was impeded by the inertia and viscosity of the dielectric liquid around the bubble, in the early discharge stage the volume of bubble was very small, as shown at 1.0 ps in Fig. 3, but the pressure inside the bubble would be extremely high, as shown in the ascending stage of the curve in Fig. 4. The liquid around the bubble was gradually speeded up and moved by the expanding bubble. At the same time, the electrode material was also melted and evaporated under the extremely high temperature, which led to the volume expansion of the molten and evaporated electrode material as shown in Fig. 5. Part of the molten and evaporated electrode material was thrown into the gap and mixed together with the gas as shown from 1.4 ps to 4.8 ps in Fig. 5. Thus, during the discharge duration from 0 ps to 4.8 ps, the pressure in the bubble was extremely high, making the mixed gas and removal material expand around, and in this process, part of the removed material from the electrodes was carried away from the gap by the expanding bubble and flowing liquid.After the end of the discharge, the pressure inside the bubble was still large enough, i.e. 242 MPa at 4.8 ps in Fig. 4, making the bubble continue to expand as shown in Fig. 3. The gap would be occupied by the expanding bubble whose diameter could be several tens of times larger than the gap width, as shown at 22.8 ps and 69.6 ps in Fig. 5. But the pressure inside the bubble was gradually decreasing with the expansion of the bubble as shown in the descending stage of the curve in Fig. 4. Although the later expanding and shrinking processes could not be obtained in this study due to the limitations of this simulation model, it could be found from the curve trend in Fig. 4 that the pressure inside the bubble would continue to decrease with the expansion of bubble until the pressure inside the bubble was below the atmospheric pressure, leading to the oscillation of the bubble.24 It could be also found from the direction of the velocity vectors in Fig. 4 that the gas molecules moved away from the discharge channel and expanded outside, and the modulus of the velocity vectors showed that at the beginning of the discharge stage, the gas velocity was much higher in the bubble and then decreased gradually as the discharge time went on, which could reflect the change in the trend of the pressure inside the bubble indirectly. Meanwhile, the picture at 6.0 ps in Fig. 5 showed that after the end of the discharge, there was still much material being removed from the electrodes, and much removed material had no time to be taken away from the gap and flocked together between the anode and cathode.
The overheated theory, which could be traced back to the study of Zolotykh,25 asserted that the material ablation in EDM happened after the end of the discharge and was caused by the collapse of the bubble. For example, Hockenberry et al.26 believed that the molten material was sprayed by a liquid jet which was driven by the shrinking and fragmenting bubble when the expanding bubble began to collapse and shrink due to the pressure inside the bubble being below the atmospheric pressure after the end of the discharge. Also, van Dijck et al.27 thought that the overheated and boiling electrode material was suppressed by the extremely high pressure inside the bubble during the discharge duration and then ablated at the end of the discharge for the boiling ablation as the pressure inside the bubble decreased. But the results in Fig. 5 show that although the pressure inside the bubble during the discharge process was extremely high and could be hundreds of megapascals, as shown in Fig. 4, material was still ablated. In addition, research results by Yang et al. showed that when the pressure gradient overcomes the bonding strength among atoms, the atoms or clusters can be ablated off of the electrode.22 Thus, we can conclude that it was not the case that the molten material could not be removed during the discharge duration as was stated by the overheated theory,25–27 but the case that during the whole of the discharge duration, material ablation would occur all of the time, and even after the end of the discharge, molten material could still be ablated for a period of time.
4. Influence of the bubble and the dielectric liquid
4.1 Influence on the distribution of the crater material
In order to reveal the influence of the bubble and flowing liquid on the material distribution, the material classification was defined, as shown in Fig. 6, and its distribution, as shown in Fig. 7, was analyzed statistically. We take the anode as the example, as the cathode has the same distribution regularity.In Fig. 6(a), the material which was moved out from the crater was called the crater material. The simulation results in Fig. 6(b) showed that the crater material could be classified into four parts: the first part of the crater material that becomes debris in the gap could be called the removal debris, which was symbolized by the hollow circle in Fig. 6(a); the second part settles on the surface of the opposite electrode and could be named the spattering material, which was symbolized by the semi solid circle in Fig. 6(a); the third part returns to the surface of the electrode from which it was ejected and could be called the returning material, this was symbolized with the solid circle in Fig. 6(a); and the last part, forming the main part of bulge, could be known as the bulge material. The simulation results also showed that the bulge was formed for two reasons: the main reason was the shearing flow of the molten material that formed the bulge material and the other was the accumulation of a portion of the returning material and a portion of the spattering material,21 as shown in Fig. 6(a). The bulge material and the returning material in the bulge mixed together and could not be distinguished, while the spattering material in the bulge could easily be picked out by the program. Moreover, in this study, we mainly focus on the influence of the bubble and deionized water on the removal debris and the spattering material. Thus, the returning and bulge material was considered as a whole part in the quantitative statistics of the crater material.
The simulation results in the left part of Fig. 7 showed that in the case of a discharge in deionized water, 64.72% of the crater material from the anode became bulge material or returning material, 18.36% of the crater material from the anode spattered on the surface of the opposite electrode, and 16.92% of the crater material from the anode was removal debris. The above distribution in gas was 70.46%, 21.76% and 7.78%, respectively. Moreover, the simulation results in the right part of Fig. 7 showed that the number of atoms of the crater material in deionized water was lower than that in gas, which will be explained particularly in Section 4.3.
The reason why the proportion of spattering material in the dielectric liquid was much smaller than that in gas can be explained as follows. In the case of a discharge in deionized water, the removed material must firstly enter the bubble and liquid, and then penetrate the high-pressure bubble and flowing liquid, and finally may spatter on the surface of the opposite electrode. In the above process, the removed material would be blocked by the expanding bubble and flowing liquid, making some of the removed material decelerate greatly, and as a result some of the removed material will fail to reach the surface of the opposite electrode. Whereas in the case of gas, the resistance is lower than that in the high-pressured bubble and flowing liquid, allowing much more removal material to reach the surface of the opposite electrode.
In the case of deionized water, the total proportion of the returning material and bulge material was smaller than that in gas mainly for two reasons. On the one hand, the resistance that the returning material suffered in deionized water is much larger than that in gas, causing a reduction in the returning material. On the other hand, the expanding bubble and flowing liquid have a removal effect on the bulge (the removal effect will be explained and discussed in detail in Section 4.3), making the bulge in deionized water smaller than the one in gas. Based on the above two reasons, the total proportion of the returning material and bulge material in deionized water was smaller than that in gas.
Based on the above analysis, we know that compared with a discharge in gas, in the case of a discharge in deionized water, not only the proportion of the bulge and returning material, but also the proportion of the spattering material decreased, leading to an increase in the proportion of removal debris.
In summary, we could draw two important conclusions. First of all, EDM can be carried out without a dielectric liquid. In gas, however, much more removal material spatters on the surface of the opposite electrode and returns to the surface of the original electrode, which causes a much lower material removal rate. Secondly, the dielectric liquid does not play a critical role in material removal, but has the very important function of carrying away the removal material and hindering the removed material from spattering or returning, which causes a much higher material removal rate.
4.2 Influence on the velocity and volume distribution of the removal debris
In order to clarify the influence of the bubble and the flowing liquid on the removal debris, the velocity and volume distribution of the removal debris, as shown in Fig. 8, was analyzed. It should be noted that material debris in the same dotted rectangle has the same volume, which was labeled on the top of the rectangle: 1.176 × 10−2 nm3, 2.352 × 10−2 nm3 and 3.528 × 10−2 nm3. But in order to distinguish between the material debris generated in deionized water or gas easily, the distribution of the material debris generated in deionized water was offset to the right at some distance along the horizontal coordinate, as shown in the dotted rectangles in Fig. 8. It could be found from Fig. 8 that compared with a discharge in deionized water, the range of the velocity distribution of the removal debris in gas was much larger. The largest velocity of removal debris in gas could reach 5.2 km s−1 which was far more than the 1.6 km s−1 in deionized water. Besides this, the average velocity of the removal debris with the same volume in gas was also far more than that in deionized water. Moreover, the average velocity of all of the removal debris in gas was 1.9 km s−1, contrasting with 0.8 km s−1 in deionized water. The above phenomena can be explained as follows. Removal debris in deionized water suffers resistance from not only expanding bubble, but also the flowing liquid, which would slow down the removal debris greatly. Whereas in gas, the gas resistance is much smaller than that of deionized water. | ||
| Fig. 8 Relationship between the velocity and volume of the removal debris after the end of the discharge. A logarithmic scale is adopted for the horizontal coordinates. | ||
In addition, from Fig. 8, we could also find that the range of the volume distribution of the removal debris in deionized water was much larger than that in gas. The largest volume of removal debris in deionized water could reach 94 × 10−2 nm3 which was far more than the 8.4 × 10−2 nm3 in gas. It is because the removal debris in gas, whose velocity is much higher than that in deionized water, could be dissociated into small volume particles more easily due to collisions among the removed material. Thus, the range of volume distribution of the removal debris in deionized water was much larger than that in gas. Besides this, the volume distribution of the removal debris was mainly within 1–10 × 10−2 nm3 and 1–4 × 10−2 nm3 in deionized water and in gas, respectively, indicating that smaller volume particles take a dominant position among the removal debris in nano EDM.
4.3. Influence on the bulge and discharge crater
The influence of the bubble and flowing liquid on the bulge and crater is analyzed in this section using Fig. 7, 9, and 10. It can be found from Fig. 9 that the bulge generated in gas was much bigger and plumper compared with the small and fragmentary bulge generated in deionized water. In addition, the simulation results showed that the volume of the bulge on the anode in gas was 36% more than that in deionized water under the same simulation conditions. The above result can be explained with Fig. 10. In the case of a discharge in deionized water, as shown in Fig. 10(a), the expanding velocity of the bubble can be very large, making the dielectric liquid expand around it at the same high speed. Thus, in deionized water, part of the molten bulge is sheared from the surface of the electrode and carried away by the flowing liquid and expanding bubble, as shown in the circle in Fig. 10(a). While the molten bulge in gas, shown by the circle in Fig. 10(b), suffers few effects from the gas, making the bulge much bigger and plumper than that in deionized water, as shown in Fig. 9. | ||
| Fig. 10 Middle section view of the bulge during the formation process (t = 4.0 ps) in deionized water (a) and gas (b). | ||
Additionally, it can be found from the right part of Fig. 7 that the number of atoms of the crater material generated in gas was much larger than that in deionized water with the same simulation conditions. The reason can be explained as follows. In the case of a discharge in deionized water, the high-pressure bubble and flowing liquid can impose pressure on the molten region, which will block the removal of the molten material to some extent. That is, the hydrostatic pressure inside the molten region22 must not only overcome the chemical bonds among the atoms, but also the pressure outside the electrodes, then the material can be removed from electrodes. Whereas in the case of a discharge in gas the hydrostatic pressure inside the molten region only needs to overcome the chemical bonds among the atoms because of the negligible gas pressure outside the electrodes. Therefore, material removal in gas can happen much more easily. It should be noted that during actual EDM, the expanding velocity of the discharge column in a dielectric liquid is different from that in gas, thus the energy density of the discharge column in a dielectric liquid is also different from that in gas, which can also cause the difference in the volume of the discharge crater. Although the expanding velocity of the discharge column was considered to be the same in both the dielectric liquid and gas in this study, the simulation result indeed demonstrates that the bubble and dielectric liquid have a blocking effect on material removal. The above conclusion cannot be obtained using the FEM method or by experiments.
5. Conclusions
In this paper, a nano EDM process with a single pulse discharge was simulated in deionized water. Moreover, not only the bubble formation and early expanding processes, but also the function of the bubble and the dielectric liquid were analyzed. The following conclusions were obtained.(1) It was not the case that molten material could not be removed during the discharge duration, but the case that material removal would occur all of the time during the whole duration of the discharge, and even after the end of the discharge, the molten material could still be ablated for a period of time.
(2) In the early discharge stage, since the expansion of the bubble was impeded by the inertia and viscosity of the dielectric liquid, the pressure inside bubble would be extremely high. In addition, after the end of the discharge, the bubble would continue to expand and occupy the gap, which would be several tens of times larger than the gap width.
(3) Due to the removal and carrying effect of the bubble and liquid, the proportion of removal debris in deionized water was far more than that in gas, while the proportion of spattering material, returning material and bulge material was lower than that in gas.
(4) The range of the volume distribution of the removal debris in deionized water was larger than that in gas, but the range of the velocity distribution of removal debris was lower than that in gas.
(5) The bulge generated in gas was much larger and plumper compared with the small and fragmentary bulge generated in deionized water.
(6) The high-pressure bubble and flowing liquid have a blocking effect on the material removal process, which will result in the volume difference of the discharge crater generated in deionized water and gas.
Acknowledgements
The authors would like to thank the National Natural Science Foundation of China (General Program, 51175121) for providing financial support for this research and American Sandia National Laboratories for their free and open source software (LAMMPS).References
- R. J. Ji, Y. H. Liu, Y. Z. Zhang, B. P. Cai, H. Li and J. M. Ma, Int. J. Adv. Des. Manuf. Technol., 2010, 51, 195–204 CrossRef.
- R. J. Ji, Y. H. Liu, Y. Z. Zhang, F. Wang, B. P. Cai and H. Li, Chin. Sci. Bull., 2012, 57, 421–434 CrossRef CAS.
- F. Han, Y. Yamada, T. Kawakami and M. Kunieda, Precis. Eng., 2006, 30, 123–131 CrossRef PubMed.
- A. Kojima, W. Natsu and M. Kunieda, CIRP Ann. Manuf. Technol., 2008, 57, 203–207 CrossRef PubMed.
- M. Kunieda, H. Takeuchi and Y. Kusakabe, International Journal of Electrical Machining, 2011, 16, 15–19 Search PubMed.
- H. P. Schulze, G. Wollenberg, S. Matzen and K. Mecke, Proc. 15th CIRP Conf. on Electro Physical and Chemical Machining, Pittsburgh, 2007, pp. 217–220 Search PubMed.
- M. Yoshida and M. Kunieda, International Journal of Electrical Machining, 1998, 3, 39–46 Search PubMed.
- J. Wang, F. Z. Han, G. Cheng and F. L. Zhao, Int. J. Mach. Tool. Manufact., 2012, 58, 11–18 CrossRef PubMed.
- H. Takeuchi and M. Kunieda, Proc. 15th CIRP Conf. on Electro Physical and Chemical Machining, Pittsburgh, 2007, pp. 63–68 Search PubMed.
- Y. Z. Zhang, Y. H. Liu, R. J. Ji, C. Zheng, Y. Shen and X. L. Wang, Int. J. Adv. Manuf. Tech., 2013, 68, 1707–1715 CrossRef.
- A. Okada, Y. Uno, S. Onoda and S. Habib, CIRP Ann. Manuf. Technol., 2009, 58, 209–212 CrossRef PubMed.
- A. M. Naserian-Nik, M. Tahani and M. Karttunen, RSC Adv., 2014, 4, 10751–10760 RSC.
- M. M. Islam, A. Ostadhossein, O. Borodin, A. T. Yeates, W. W. Tipton, R. G. Hennig, N. Kumar and A. C. T. van Duin, Phys. Chem. Chem. Phys., 2015, 17, 3383–3393 RSC.
- J. Azamat, J. J. Sardroodi and A. Rastkar, RSC Adv., 2014, 4, 63712–63718 RSC.
- L. Zhang, H. W. Zhao, L. Dai, Y. H. Yang, X. C. Du, P. Y. Tang and L. Zhang, RSC Adv., 2015, 5, 12678–12685 RSC.
- M. Kunieda, A. Hayasaka, X. D. Yang, S. Sano and I. Araie, CIRP Ann. Manuf. Technol., 2007, 56, 213–216 CrossRef PubMed.
- K. Egashira, Y. Morita and Y. Hattori, Precis. Eng., 2010, 34, 139–144 CrossRef PubMed.
- A. P. Malshe, K. Virwani, K. P. Rajurkar and D. Deshpande, CIRP Ann. Manuf. Technol., 2005, 54, 175–178 CrossRef.
- K. R. Virwani, A. P. Malshe and K. P. Rajurkar, CIRP Ann. Manuf. Technol., 2007, 56, 217–220 CrossRef PubMed.
- K. R. Virwani, A. P. Malshe and K. P. Rajurkar, Phys. Rev. Lett., 2007, 99 Search PubMed.
- X. D. Yang, J. W. Guo, X. F. Chen and M. Kunieda, Precis. Eng., 2011, 35, 51–57 CrossRef PubMed.
- X. Yang, X. Han, F. Zhou and M. Kunieda, Proc. 17th CIRP Conf. on Electro Physical and Chemical Machining, Leuven, 2013, pp. 432–437 Search PubMed.
- X. Heng, K. Masanori and N. Nishiwaki, International Journal of Electrical Machining, 1996, 1, 45–52 Search PubMed.
- M. Kunieda, B. Lauwers, K. P. Rajurkar and B. M. Schumacher, CIRP Ann. Manuf. Technol., 2005, 54, 599–622 Search PubMed.
- B. N. Zolotykh, Sov. Phys. Tech. Phys., 1959, 4, 1370–1373 Search PubMed.
- T. O. Hockenberry and E. M. Williams, IEEE Trans. Ind. Gen. Appl., 1967, 4, 302–309 CrossRef.
- F. van Dijck, Ph. D. Thesis, University of Katholieke Universiteit Leuven, 1973.
| This journal is © The Royal Society of Chemistry 2015 |








