Structural, mechanical, thermodynamic and electronic properties of AgIn2 and Ag3In intermetallic compounds: ab initio investigation
Ching-Feng Yua,
Hsien-Chie Cheng*b and
Wen-Hwa Chen*a
aDepartment of Power Mechanical Engineering, National Tsing Hua University, Hsinchu 30013, Taiwan. E-mail: whchen@pme.nthu.edu.tw; Tel: +886-3-5742913
bDepartment of Aerospace and Systems Engineering, Feng Chia University, Taichung 40724, Taiwan. E-mail: hccheng@fcu.edu.tw; Tel: +886-4-24517250 extn 3979
First published on 7th August 2015
Abstract
The structural, mechanical, thermodynamic and electronic properties of two Ag–In phase crystals, i.e., AgIn2 and Ag3In intermetallic compounds (IMCs), are explored using ab initio calculations within the generalized gradient approximation. The optimized lattice constants of AgIn2 and Ag3In crystals are first investigated in the study. Next, the elastic constants of the two single crystal structures as well as their associated polycrystalline elastic properties, such as bulk modulus, Young's modulus, shear modulus and Poisson's ratio, are predicted through Voigt–Reuss–Hill approximation. The mechanical characteristics of these two crystals, such as ductile–brittle characteristic and elastic anisotropy, are further assessed by way of the calculation of the Cauchy pressures, Zener anisotropy factor and directional Young's modulus. Additionally, the temperature-dependence of Debye temperature and heat capacity are obtained according to a quasi-harmonic Debye model, and their band structures and density of states profiles are evaluated through analysis of electronic characteristics. The calculation results show that these two IMC crystals are not only an elastically anisotropic, low stiff and very ductile material but also a conductor. The elastic anisotropy, mechanical property, Debye temperature and heat capacity of Ag3In all surpass those of AgIn2, and also, Ag3In tends to be much stiffer than AgIn2. Furthermore, the heat capacity of these two crystals strictly follows with the well-known T3-law at temperature below the Debye temperature and would reach the Dulong–Petit limit at temperature above the Debye temperature.
1. Introduction
To meet the trend toward green products in the microelectronic packaging industry,1 numerous studies have been made to develop lead-free solders.2,3 Nowadays, a substantial number of novel multi-component Pb-free alloys have been proposed as potential alternative to Pb–Sn solders,4–6 in which some metal elements such as In, Bi, Sb and Zn, in replacement of Pb, are doped into solders. Among these metal elements, In-based alloy solders, as well as pure indium, may be the most promising candidates due to their outstanding wettability, low melting point, high thermal fatigue durability and high ductility.7–10 Thus, these extraordinary properties make In-based solders attractive for bonding temperature sensitive devices that need low process temperature and high ductility, such as the bond interconnect between central processing unit chips and Cu heat-sinks, light-emitting diodes and thermal inductive sensors.11Unfortunately, there are many important technical challenges needed to be solved before they can be successfully implemented as an interconnect material. For instance, the Cu pads coated with Ag film are used as the under bump metallurgy (UBM) of chip and substrate metallization for solder bonding in the microelectronics industry.12,13 During the solder joint assembly process of solder joints on Ag pad, the Ag surface finish dissolves into the liquid In-based solder, leading to the precipitation of Ag–In phase intermetallic compounds (IMCs), such as AgIn2 and Ag3In, at the interfaces between the solder and UBM. The IMCs can effectively prompt a remarkable influence on the structural stiffness and material strengths of solder joints, which are significant to the reliability performance of the microelectronic packaging.14 In literature, extensive investigations have put their focus on the interfacial formation and evolution of AgIn2 and Ag3In IMCs.11,13–20 It is worth noting that prior to the successful application of the Pb-free solder in the advanced interconnect technology, it is very crucial to thoroughly grasp the physical properties of the IMCs for further comprehension of the solder joint reliability. The main goal of the study attempts to provide a more complete and comparative investigation of the structural, mechanical, thermodynamic and electronic properties of the AgIn2 and Ag3In IMCs through ab initio calculations by density functional theory (DFT)21–23 within the generalized gradient approximation (GGA).22
2. Computational details
In the study, the ab initio DFT calculations are carried out by means of the Cambridge Serial Total Energy Package code.24,25 The interactions between electrons and core ions are treated using the ultrasoft pseudopotential.26 The exchange-correlation energy is described within GGA of the Perdew–Burke–Ernzerhof formalism,22 which is dependent on both the electron density and its gradient at each space point. After performing careful tests of convergence, it is found that a cutoff energy of 350 eV is sufficient to reduce the error in the total energy less than 0.1 meV per atom.27,28 For sampling of the Brillouin zone, the Monkhorst–Pack point meshes29 of 8 × 8 × 10 and 12 × 12 × 12 are employed for AgIn2 and Ag3In. A quasi-Newton (variable-metric) minimization method using the Broyden–Fletcher–Goldfarb–Shanno update scheme30 is applied to search the ground state. The system would attain the ground state via self-consistent calculation as the total energy is stable less than 5 × 10−6 eV per atom, the maximum displacement of atoms is 5 × 10−4 Å, the maximum ionic Hellmann–Feynman force is less than 0.01 eV Å−1 and the maximum stress below 0.02 GPa.3. Results and discussion
3.1. Structural properties
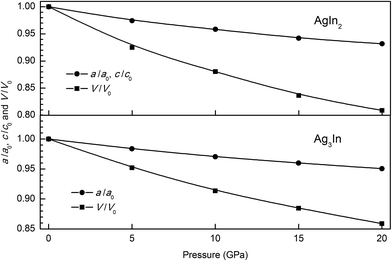
The lattice constants and the atomic positions of AgIn2 and Ag3In crystals are first optimized according to the reported experimental crystal structures31–33 through X-ray diffraction analysis, as shown in Fig. 1. It reveals the AgIn2 and Ag3In crystals belong to the lattice system of tetragonal and cubic, respectively. The optimized lattice constants, lattice constant ratios (c/a) and equilibrium volume in the ground state are given in Table 1, together with the previous experimental results for comparison. A good agreement can be found between present results and the previous experimental values.31–33 However, there is a fair discrepancy in the equilibrium volume between them, which could be mainly due to the well-known overestimation problem using GGA. Fig. 2 shows hydrostatic pressure-induced variation of the relative change of the lattice constants (a/a0 and c/c0) and unit cell volume (V/V0), where a0, c0 and V0 denote the lattice constants and volume at ambient pressure. Apparently, the a/a0, c/c0 and V/V0 considerably decease with the increase of hydrostatic pressure, revealing that the hydrostatic pressure would reduce the size of the unit cell of AgIn2 and Ag3In crystals. | ||
| Fig. 1 Crystal structures of (a) AgIn2 and (b) Ag3In. The big spheres in brown are In atoms and the small spheres in blue are Ag atoms. | ||
| Lattice constants (Å) | Lattice constant ratio | V (Å3) | K (GPa) | G (GPa) | E (GPa) | v | K/G | |
|---|---|---|---|---|---|---|---|---|
| a Ref. 31.b Ref. 32.c Ref. 33. | ||||||||
| AgIn2 | a = b = 6.99, c = 5.75, (a = b = 6.87, c = 5.60)a (a = b = 6.88, c = 5.62)b | c/a = 0.822 (c/a = 0.817)a | 280.95 (266.12)a (264.30)b | 50.09 | 23.93 | 61.93 | 0.294 | 2.09 |
| Ag3In | a = b = c = 4.23 (a = b = c = 4.14)c | — | 75.69 (70.96)c | 83.22 | 31.86 | 84.76 | 0.330 | 2.61 |
3.2. Elastic and mechanical properties
Elastic constants can generally give a link between the mechanical and dynamical behaviors of crystals and give important information concerning the nature of chemical bonding operating in solids. For the tetragonal AgIn2 crystal, there are six independent elastic constants, namely, C11, C33, C44, C66, C12 and C13, in the stiffness matrix. On the other hand, for the stiffness matrix of cubic Ag3In crystal, it comprises three independent elastic constants, including C11, C44 and C12. The independent elastic constants can be obtained by a linear fit to the stress–strain relationship according to the Hooke's law as applying an appropriate infinitesimal strain pattern to generate stresses. It should be noted that the calculated elastic constants for the crystals should satisfy the following mechanical stability criteria.For tetragonal crystal:
| C11 > 0, C33 > 0, C44 > 0, C66 > 0, | (1) |
| C11 − C12 > 0, C11 + C33 − 2C13 > 0 | (2) |
| {2(C11 + C12) + C33 + 4C13} > 0. | (3) |
For cubic crystal:
| C11 + 2C12 > 0, C44 > 0, C11 − C12 > 0. | (4) |
By substituting all these calculated elastic constants into the above equations (i.e., eqn (1)–(4)), it is demonstrated that the present calculations do match all the above criteria, suggesting that these two single crystals are intrinsically stable system. Moreover, the pressure dependence of the elastic constants for AgIn2 and Ag3In is assessed, and the results are presented in Fig. 3. Noticeably, there is a quasi-linear dependence between the elastic constants and hydrostatic pressure for the two crystals as the applied hydrostatic pressure is in the range of 0–20 GPa. It can be mainly attributed to the pressure-dependent lattice constants, which would decrease with pressure, as shown in Fig. 2, thereby leading to a greater stiffness. Further by comparing these elastic constants, it is clearly found that C11, C33, C12 and C13 are susceptible to the hydrostatic pressure, while C44 and C66 vary little under the effect of the hydrostatic pressure.
It is generally noted that the angular character of atomic bonding is related to material characteristics, such as brittleness or ductility. Pettifor34 signified that Cauchy pressure can be adopted to capture the nature of the bonding. The materials with a positive Cauchy pressure possess metallic like bonds, thereby holding ductile characteristics. On the other hand, brittle materials would possess a negative Cauchy pressure. For the tetragonal AgIn2 crystal, the Cauchy pressure can be depicted by two terms, i.e., C12–C66 and C13–C44. On the contrary, there is only one term for the cubic Ag3In crystal to calculate the Cauchy pressure, denting as C12–C44. The calculated Cauchy pressures for AgIn2 and Ag3In single crystals as a function of pressure are shown in Table 2. It is found the Cauchy pressures for AgIn2 and Ag3In single crystals are all positive, suggesting that these two crystals would hold a ductile behavior. In addition, an increasing hydrostatic pressure would enhance the Cauchy pressures, which indicates that the ductility of AgIn2 and Ag3In single crystals increase with the hydrostatic pressure. By comparing the calculated these Cauchy pressures, one can see that the increasing trend of Cauchy pressure, induced by the hydrostatic pressure, of AgIn2 is larger than that of Ag3In.
| Pressure (GPa) | AZ | C12–C44 (GPa) | C12–C66 (GPa) | C13–C44 (GPa) | Hv (GPa) | |
|---|---|---|---|---|---|---|
| 0 | AgIn2 | 1.46 | — | 11.73 | 10.55 | 3.76 |
| Ag3In | 2.01 | 25.68 | — | — | 5.37 | |
| 5 | AgIn2 | 1.59 | — | 33.65 | 28.07 | 3.16 |
| Ag3In | 2.33 | 29.81 | — | — | 5.10 | |
| 10 | AgIn2 | 1.68 | — | 42.07 | 43.74 | 2.92 |
| Ag3In | 2.85 | 41.64 | — | — | 5.02 | |
| 15 | AgIn2 | 1.98 | — | 72.66 | 68.42 | 2.56 |
| Ag3In | 3.80 | 62.69 | — | — | 4.87 | |
| 20 | AgIn2 | 2.64 | — | 104.44 | 89.43 | 2.18 |
| Ag3In | 5.47 | 84.96 | — | — | 3.58 |
The elastic anisotropy of crystals would have a great effect on the physical properties, such as anisotropic plastic deformation, crack behavior and elastic instability. To quantify the degree of anisotropy of a solid, the Zener anisotropy factor (AZ)35–37 is usually applied, as shown below.
For tetragonal crystal:
 | (5) |
For cubic crystal:
 | (6) |
As the Zener anisotropy factors, AZ, is unity, crystals are considered as an isotropic system; otherwise, they are an elastically anisotropic system. A larger deviation from unity signifies a greater elastic anisotropy. The predicted Zener anisotropy factors for AgIn2 and Ag3In single crystals versus pressure are listed in Table 2. It reveals that the Zener anisotropy factor for AgIn2 and Ag3In crystals at zero pressure is around 1.46 and 2.01, respectively, which suggests that Ag3In single crystal is composed of a much higher degree of elastic anisotropy than AgIn2. Table 2 further shows the Zener anisotropy factor for AgIn2 and Ag3In crystals significantly increases with the hydrostatic pressure, implying that the elastic anisotropy of these two single crystals would rapidly rise as the hydrostatic pressure increases from 0 to 20 GPa.
To further evaluate the anisotropic characteristics of AgIn2 and Ag3In crystals, a three-dimensional surface representation of the elastic anisotropy of the two single crystals is attempted. The representation demonstrates the variation of the Young's modulus of the crystals with crystal direction. The direction dependence of the Young's modulus of tetragonal and cubic crystal systems can be expressed as,38.
For tetragonal crystal:
| E = 1/((l14 + l24)s11 + l34s33 + l12l22(2s12 + s66) + l32(1 − l32)(2s13 + s44)). | (7) |
For cubic crystal:
| E = 1/(s11 + 2(s11 − s12 − 0.5s44)(l12l22 + l22l32 + l32l12)). | (8) |
 | ||
| Fig. 4 Direction dependence of Young's modulus and their projections onto the a–b, b–c and a–c planes for (a) AgIn2 and (b) Ag3In crystals (unit: GPa). | ||
Generally speaking, the bulk modulus (K) is the measure of resistance to volume change by applied hydrostatic pressure, and shear modulus (G) is the measure of resistance to reversible deformation upon shear stress. Young's modulus (E) reveals the resistance of materials against uniaxial tensions. The Poisson's ratio (v) is normally used to quantify the stability of the crystal against shear deformation, which is in the range of −0.5–0.5, and the larger the Poisson's ratio, the better the plasticity. These polycrystalline mechanical properties are very important for industrial applications, and they can be determined based on the following Voigt–Reuss scheme39 in terms of independent elastic constants,
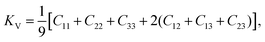 | (9) |
| KR = [S11 + S22 + S33 + 2(S12 + S13 + S23)]−1, | (10) |
 | (11) |
| GR = 15[4(S11 + S22 + S33) − 4(S12 + S13 + S23) + 3(S44 + S55 + S66)]−1. | (12) |
The above formulate yield the upper (Voigt) and lower (Reuss) bounds of the polycrystalline elastic properties. Furthermore, the Voigt–Reuss–Hill approximation40 is utilized to give the effective values of the bulk and shear modulus,
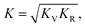 | (13) |
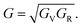 | (14) |
Then, the Young's modulus and the Poisson's ratio of the AgIn2 and Ag3In IMCs can be calculated by using the bulk and shear modulus,
 | (15) |
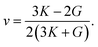 | (16) |
The obtained bulk modulus, shear modulus, Young's modulus and Poisson's ratio for the polycrystalline AgIn2 and Ag3In are shown in Table 1. Evidently, it is found that these four results (i.e., K, G, E and v) of Ag3In are larger than those of AgIn2. In addition, the hydrostatic pressure dependence of the polycrystalline mechanical properties of the AgIn2 and Ag3In IMCs are also examined, as can be seen in Fig. 5. By further comparing the results in the figure, it is found that the pressure has a much larger impact on the bulk modulus, as compared to the shear modulus and Young's modulus. The degree of variation in the bulk modulus with the pressure range of 0–20 GPa can be as much as about 203% and 127% for AgIn2 and Ag3In IMCs, respectively.
 | ||
| Fig. 5 The calculated bulk modulus, shear modulus and Young's modulus as a function of hydrostatic pressure of the polycrystalline AgIn2 and Ag3In IMCs. | ||
To recognize the brittle and ductile behavior of materials, Pugh41 has presented a relationship, which empirically identifies the plastic properties of materials by the ratio of the bulk modulus to shear modulus. The critical value for separating ductile and brittle materials is around 1.75. If K/G ratio is over 1.75, the material behaves in a ductile way; otherwise the material behaves in a brittle way. The calculated K/G ratios for AgIn2 and Ag3In at zero pressure are exhibited in Table 1. It is found that the K/G ratios are larger than 1.75, revealing the AgIn2 and Ag3In IMCs are completely ductile materials. Table 1 further demonstrates that the K/G ratio of Ag3In is larger than that of AgIn2, suggesting that the Ag3In crystal is much more ductile than AgIn2.
The hardness of a material generally plays an essential role in its applications, especially using as an abrasive resistant phase. Teter42 found a linear correlation of Vickers hardness Hv with shear modulus G. Nevertheless, the hardness is not only associated with the shear modulus G, but also the bulk modulus K for many materials. In the quest for a better formula, an amendatory non-linear correlation formula associated with K and G has been proposed by Chen et al.,43
| Hv = 2(k2K)0.585 − 3, k = G/K. | (17) |
However, Tian et al.44 reported that eqn (17) may make the hardness negative for some low hardness materials due to the “−3” term, so they modified it which then can always obtain positive values. In the study, the correction by Tian et al.44 is adopted to calculate the Vickers hardness of the AgIn2 and Ag3In, as described below,
| Hv = 0.92k1.137G0.708, k = G/K. | (18) |
The calculated Vickers hardness Hv associated with these two polycrystalline IMC crystals as a function of hydrostatic pressure are listed in Table 2. It turns out that they are all a low stiff material, and the low Vickers hardness of the two polycrystalline IMC crystals may be attributed to the weak metal bond. The results also reveal that the Vickers hardness of Ag3In at various pressures are all lager than those of AgIn2, suggesting that the Ag3In is much stiffer than AgIn2. Additionally, the hydrostatic pressure would also have a substantial influence on the Vickers hardness, where the Vickers hardness would decrease with the hydrostatic pressure.
3.3. Thermodynamic properties
In order to investigate thermodynamic properties of AgIn2 and Ag3In IMCs, the quasi-harmonic Debye model is applied, in which the phonon effect is considered. This model is described in detail in ref. 45 and 46. In the quasi-harmonic Debye model, the non-equilibrium Gibbs function G*(V;P,T) is taken in the form of,| G*(V;P,T) = E(V) + PV + AVib(θ(V);T), | (19) |
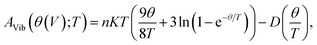 | (20) |
 is the Debye integral given as,
is the Debye integral given as,
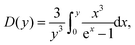 | (21) |
 | (22) |
 | (23) |
The f(v) function is given in48,49 and the Poisson's ratio v is determined through calculated elastic constants. Then, the nonequilibrium Gibbs function G*(V;P,T) can be minimized with respect volume V as follow,
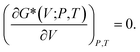 | (24) |
By solving equation, the thermal equation of state V(P,T) can be obtained. The heat capacity is expressed as,50
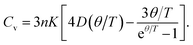 | (25) |
The calculated Debye temperature and heat capacity as function of hydrostatic pressure and temperature of AgIn2 and Ag3In are shown in Fig. 6 and 7. The analysis results show that the Debye temperature is nearly independent of the temperature at the temperature range of 0–1000 K. Moreover, under a fixed temperature, the Debye temperature increases with the hydrostatic pressure. As the pressure increases from 0 to 20 GPa, the Debye temperature for AgIn2 and Ag3In at 300 K would increase by about 47% and 40%, respectively. At zero pressure and 300 K, the calculated Debye temperature for AgIn2 and Ag3In are about 179.8 and 199.9 K. Fig. 7 reveals the temperature dependence of the heat capacity of AgIn2 and Ag3In. It is found that the heat capacity at low temperatures shows high-temperature dependence, i.e., the third power of temperature, which is a consequence of the Debye T3 law.51 However, at temperature above the Debye temperature, the heat capacity tends to reach the well-known Dulong–Petit limit,52 i.e., about 12.3 and 24.4 J mol−1 K for AgIn2 and Ag3In, which is common to all solids at high temperature or a temperature far above the Debye temperature. Additionally, it can be also observed from the figure that the heat capacity increases with temperature at a constant pressure while decreasing with pressure at a constant temperature. By further looking at Fig. 7, it is clear to see that temperature tends to have a greater impact on the heat capacity of the crystal than pressure within the temperature and pressure range studied.
 | ||
| Fig. 6 Variation of Debye temperature as a function of temperature for (a) AgIn2 and (b) Ag3In IMCs. | ||
3.4. Electronic properties
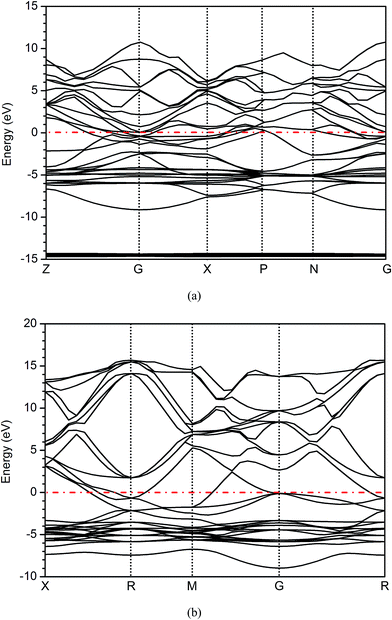
The calculated energy band structures of AgIn2 and Ag3In IMCs along the high symmetry directions in the first Brillouin zone are shown in Fig. 8. It is evident that the valence and conduction bands overlap with each other and there is no band gap at the Fermi level, indicating that AgIn2 and Ag3In IMCs are not insulator or semiconductor. In order to elucidate the major contribution of orbit in the band structure and bonding characteristics, the total density of state (TDOS) and partial density of state (PDOS) of AgIn2 and Ag3In IMCs are investigated, as can be seen in Fig. 9. There is no band gap for AgIn2 and Ag3In IMCs, and TDOS of AgIn2 and Ag3In IMCs at the Fermi level are N(EF) = 2.583 and 1.326 electrons per eV, respectively. Furthermore, TDOS indicates that there is an energy gap from −13.40 eV to −10.00 eV for AgIn2 and −13.70 eV to −9.72 eV for Ag3In. The large peaks in TDOS from −15.62 to −13.40 eV for AgIn2 and −15.66 to −13.70 eV for Ag3In mainly drive from In-4d state. The low-wide peaks in TDOS between −9.99 and 11.12 eV for AgIn2 has contributions substantially from Ag-4d and In-5p states as well as In-5s and Ag-5s states have a little contribution. For Ag3In, the low-wide peaks in TDOS between −9.70 and 16.63 eV is mainly contributed by the Ag-4d and Ag-4p states, and the Ag-5s, In-5s and In-5p states would have scarcely any contribution to the TDOS. In addition, the PDOS of both AgIn2 and Ag3In IMCs indicate that In-5s and In-5p states are in low-lying states, and a strong hybridization can be observed in the energy range between −6 eV to −2 eV due to an overlap with Ag-4d state. | ||
| Fig. 9 Calculated total and partial density of states (TDOS and PDOS) for (a) AgIn2 and (b) Ag3In (the Fermi level is set to zero). | ||
4. Conclusions
In the study, the structural, mechanical, thermodynamics and electronic properties of the AgIn2 and Ag3In crystals are investigated for the first time by the first-principles density functional calculation, quasi-harmonic Debye model and the Voigt–Reuss–Hill approximation. Their dependences on temperature, pressure and also crystal direction are also examined. Some brief essential concluding remarks are drawn below.(1) The calculated lattice constants of both AgIn2 and Ag3In crystals are found to be in good agreement with the experimental data, implying the effectiveness of the proposed theoretical models.
(2) These two single crystals are demonstrated to be mechanically stable. Among the calculated independent elastic constants, C11, C33, C12 and C13 are sensitive to the hydrostatic pressure, while C44 and C66 vary little under the effect of the hydrostatic pressure.
(3) The predicted Cauchy pressures show that the AgIn2 and Ag3In crystals are categorized as the ductile material. Moreover, the Cauchy pressures would increase with the increase of hydrostatic pressure, and the increasing trend of Cauchy pressure of AgIn2 is larger than that of Ag3In.
(4) The Zener anisotropy factor shows that Ag3In single crystal would hold a much higher degree of elastic anisotropy than AgIn2. The result is also confirmed by the direction dependence of the Young's modulus.
(5) The mechanical properties, including bulk modulus, shear modulus and Young's modulus, of the polycrystalline AgIn2 and Ag3In crystals would also increase with the hydrostatic pressure, and the pressure has a much larger influence on the bulk modulus rather than the shear and Young's modulus. Additionally, according to the calculated the K/G ratio, it is found that the Ag3In crystal is much more ductile than AgIn2.
(6) The polycrystalline IMC crystals turn out to be a low stiff material according to the predicted Vickers hardness, mainly due to the weak metal bond. The Vickers hardness would also decrease with an increasing hydrostatic pressure.
(7) The Debye temperature of these two single crystals is independent of the temperature. Under a constant temperature, the Debye temperature would increase almost linearly with hydrostatic pressure. Besides, the Debye temperature of Ag3In is higher than that of AgIn2by as much as about 20 K.
(8) The heat capacity of these two crystals strictly follows with the well-known T3-law at temperature below the Debye temperature, where it at a solid at constant volume and pressure is proportional to the cube of temperature, and at temperature above the Debye temperature, tends to reach the Dulong–Petit limit. By contrast, it would decrease with pressure at a constant temperature. Most importantly, the heat capacity of Ag3In crystal is approximately twice that of AgIn2.
(9) The evaluated energy band structure shows that the AgIn2 and Ag3In are conductors.
(10) The analysis of the PDOS reveals that a strong hybridization can be observed in the energy range between −6 eV to −2 eV due to an overlap with Ag-4d state.
In summary, the investigation can help better explore the material properties of these two IMC crystals, and perhaps even their dependences on the thermal-mechanical reliability of the In-based lead-free solder joints.
Acknowledgements
The work is partially supported by National Science Council, Taiwan, ROC, NSC 101-2221-E-007-009-MY3, MOST 103-2221-E-007-010- and MOST 103-2221-E-035-024-MY3. The authors also thank the National Center for High-Performance Computing (NCHC) for computational resources support.References
- F. Su, W. J. Li, T. B. Lan and W. Shang, J. Mech., 2014, 30, 625–630 CrossRef
.
- D. M. Jacobson and G. Humpston, Gold Bull., 1989, 22, 9–18 CrossRef CAS
.
- J. H. Lau, C. P. Wong, N. C. Lee and S. W. Ricky Lee, Electronics Manufacturing with Lead-Free, Halogen-Free Conductive-Adhesive Materials, McGraw-Hill Handbooks, New York, 2003 Search PubMed
.
- M. N. Islam, Y. C. Chan, M. J. Rizvi and W. Jillek, J. Alloys Compd., 2005, 400, 136–144 CrossRef CAS PubMed
.
- F. Wang, M. O'Keefe and B. Brinkmeyer, J. Alloys Compd., 2009, 477, 267–273 CrossRef CAS PubMed
.
- A. A. El-Daly and A. E. Hammand, J. Alloys Compd., 2011, 509, 8554–8560 CrossRef CAS PubMed
.
- L. S. Goldmann, R. D. Herdzik, N. G. Koopman and V. C. Marcotte, IEEE Trans. Parts, Hybrids, Packag., 1977, 3, 194–198 CrossRef
.
- K. Shimizu, T. Nakanishi, K. Karasawa, K. Hashimoto and K. Niwa, J. Electron. Mater., 1995, 24, 39–45 CrossRef CAS
.
- W. K. Jones, Y. Liu, M. Shah and R. Clarke, Soldering Surf. Mount Technol., 1998, 10, 37–41 CrossRef CAS
.
- S. Wakiyama, H. Ozaki, Y. Nabe, T. Kume, T. Ezaki and T. Ogawa, in: Electronic Components and Technology Conference, Reno, Nevada, USA, 2007, pp. 610–615 Search PubMed
.
- P. J. Wang, J. S. Kim and C. C. Lee, in: Electronic Components and Technology Conference, San Diego, California, USA, 2009, pp. 1317–1321 Search PubMed
.
- C. T. Peng, C. M. Liu, J. C. Lin, H. C. Cheng and K. N. Chiang, IEEE Trans. Compon. Packag. Technol., 2004, 27, 684–693 CrossRef
.
- T. H. Chuang, C. C. Jain and S. S. Wang, J. Mater. Eng. Perform., 2009, 18, 1133–1139 CrossRef CAS
.
- F. Tai and F. Guo, Sci. China, Ser. E: Technol. Sci., 2009, 52, 243–251 CrossRef CAS
.
- R. I. Made, C. L. Gan, L. L. Yan, A. Yu, S. W. Yoon, J. H. Lau and C. K. Lee, J. Electron. Mater., 2009, 38, 365–371 CrossRef CAS
.
- C. Kind, R. Popescu, R. Schneider, E. Müller, D. Gerthsen and C. Feldmann, RSC Adv., 2012, 2, 9473–9487 RSC
.
- M. A. Haque and W. Gierlotka, International Journal of Mining, Metallurgy and Mechanical Engineering, 2013, 1, 173–177 Search PubMed
.
- C. S. Yoo, H. Wei, J. Y. Chen, G. Shen, P. Chow and Y. Xiao, Rev. Sci. Instrum., 2011, 82, 113901 CrossRef PubMed
.
- S. Sarkar, L. Balisetty, P. P. Shanbogh and S. C. Peter, J. Catal., 2014, 318, 143–150 CrossRef CAS PubMed
.
- N. Arora, B. R. Jagirdar and K. J. Klabunde, J. Alloys Compd., 2014, 610, 35–44 CrossRef CAS PubMed
.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871 CrossRef
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS
.
- Y. C. Shih, C. S. Chen and K. C. Wu, J. Mech., 2014, 30, 241–246 CrossRef
.
- R. Hao, X. Zhang, J. Qin, S. Zhang, J. Ning, N. Sun, M. Ma and R. Liu, RSC Adv., 2015, 5, 36779–36786 RSC
.
- R. Yu, X. Chong, Y. Jiang, R. Zhou, W. Yuan, W. Jiang and J. Feng, RSC Adv., 2015, 5, 1620–1627 RSC
.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef
.
- D. W. Boukhvalov and Y. W. Son, Nanoscale, 2012, 4, 417–420 RSC
.
- J. D. Tucker, Ab Initio-Based Modeling of Radiation Effects in the Ni–Fe–Cr System, Ph.D. thesis, University of Wisconsin, Madison, US, 2008
.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef
.
- J. D. Head and M. C. Zerner, Chem. Phys. Lett., 1985, 122, 264–270 CrossRef CAS
.
- E. Hellner, Z. Metallkd., 1951, 42, 17–19 CAS
.
- E. E. Havinga, H. Damsma and P. Hokkeling, J. Less-Common Met., 1972, 27, 169–186 CrossRef CAS
.
- A. N. Campbell, R. Wagemann and R. B. Ferguson, Can. J. Chem., 1970, 48, 1703–1715 CrossRef CAS
.
- D. G. Pettifor, Mater. Sci. Technol., 1992, 8, 345–349 CrossRef CAS PubMed
.
- K. Lau and A. K. McCurdy, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 8980–8984 CrossRef CAS
.
- W. H. Chen, C. F. Yu, K. N. Chiang and H. C. Cheng, Intermetallics, 2015, 62, 60–68 CrossRef CAS PubMed
.
- C. F. Yu, H. C. Cheng and W. H. Chen, J. Alloys Compd., 2015, 619, 576–584 CrossRef CAS PubMed
.
- A. Authier and A. Zarembowitch, International Tables for Crystallography D, New York, Springer Verlag, 2006, pp. 72–98 Search PubMed
.
- J. K. D. Verma and B. D. Nag, J. Phys. Soc. Jpn., 1965, 20, 635–636 CrossRef CAS
.
- R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349–350 CrossRef
.
- S. F. Pugh, Philos. Mag., 1954, 45, 823–843 CrossRef CAS PubMed
.
- D. M. Teter, MRS Bull., 1998, 23, 22–27 CrossRef CAS
.
- X. Q. Chen, H. Niu, D. Li and Y. Li, Intermetallics, 2011, 19, 1275–1281 CrossRef CAS PubMed
.
- Y. J. Tian, B. Xu and Z. S. Zhao, Int. J. Refract. Met. Hard Mater., 2012, 33, 93–106 CrossRef CAS PubMed
.
- M. A. Blanco, E. Francisco and V. Luana, Comput. Phys. Commun., 2004, 158, 57–72 CrossRef CAS PubMed
.
- E. Francisco, J. M. Recio, M. A. Blanco and A. Martin Pendás, J. Phys. Chem. A, 1998, 102, 1595–1601 CrossRef CAS
.
- M. A. Blanco, A. Martin Pendás, E. Francisco, J. M. Recio and R. Franco, J. Mol. Struct.: THEOCHEM, 1996, 368, 245–255 CrossRef CAS
.
- M. Flórez, J. M. Recio, E. Francisco, M. A. Blanco and A. M. Pendás, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 144112 CrossRef
.
- E. Francisco, M. A. Blanco and G. Sanjurjo, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 094107 CrossRef
.
- N. W. Ashcroft and N. D. Mermin, Solid State Physics, Saunders College, Philadelphia, 1976 Search PubMed
.
- P. Debye, Ann. Phys., 1912, 39, 789–839 CrossRef CAS PubMed
.
- A. T. Petit and P. L. Dulong, Ann. Chim. Phys., 1819, 10, 395–413 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2015 |