Correlation between the chromaticity, dielectric properties and structure of the binary metal pyrophosphates, Cu_(2−x)Zn_xP₂O₇

Abstract

The binary metal pyrophosphates, Cu_(2−x)Zn_xP₂O₇; x = 0.50–1.50, were synthesized via solid state reaction in order to obtain information on their solid solution phase formation. Characteristic peaks of the β-phase were detected under UV/Vis light emission in the range of 1200–1250 cm⁻¹. The P₂O₇⁴⁻ ion, analyzed through vibration, carried the O–P–O radical, P–O–P bridge, and approximate M–O bond stretching, and was identified using Raman and Fourier transform infrared (FT-IR) spectra. The corrected dielectric constant (ε_r) of the samples showed a similar value when Cu²⁺ was replaced by Zn²⁺ in the Cu₂P₂O₇ structure. However, a slightly decreasing ε_r could still be seen when the component x increased. The color of the samples with x = 0.00–1.50 exhibit a greenish hue, except for the composition with x = 2.00, which presents a colourless powder. The CIE chromaticity coordinates of Cu_(2−x)Zn_xP₂O₇; x = 0.50 to 1.50, shifted from (0.303, 0.366) to (0.292, 0.388), thus corresponding to a visible wavelength that shifted from about 506 to 512 nm, and 561 nm for x = 0.00. The phenomena of both dielectric and optical properties resulted from the changing crystal structure of the respective P₂O₇⁴⁻ cluster and octahedral M–O₆ site. Investigation of the crystal structure was carried out by using Rietveld refinement analysis, with support from the extended X-ray absorption fine structure (EXAFS) fitting technique. Furthermore, this study revealed the relationships for binary metal pyrophosphates between their structure and dielectric properties, and the correlation between their structure and optical properties, which was confirmed by the reduction in chemical bonding, bond angle, number of clusters, and distortion of the octahedral MO₆.

---

1. Introduction

Generally, divalent metal pyrophosphate salts (M₂P₂O₇; M = metal element), have a polymorphic structure. The crystal structure consists of two main parts, which consist of six oxygen atoms around a metal atom, or octahedral MO₆, and a P₂O₇⁴⁻ cluster that is caused by the polymerization of two [PO₄]³⁻ ions clustering to [P₂O₇]⁴⁻.^1,2 These phosphates have two crystallization conformations. The first is a dichromate type, with an M radius in the structure of greater than 0.97 Å in, for example, Ca₂P₂O₇, Sr₂P₂O₇, Ba₂P₂O₇, Pb₂P₂O₇, and Cd₂P₂O₇.³ The P₂O₇⁴⁻ cluster, in an eclipsed conformation, crystallizes in this group at about the center of the symmetry and P–O–P bridge, which spread towards each other. The second is a thortveitite type, with an M radius of less than 0.97 Å in, for example, Cu₂P₂O₇, Zn₂P₂O₇, Ni₂P₂O₇, Mn₂P₂O₇, Co₂P₂O₇, and Mg₂P₂O₇. This type of P₂O₇⁴⁻ cluster occurs in a staggered conformation. On the other hand, the metal pyrophosphate compounds are separated by a stable phase structure at different temperatures, which includes α-M₂P₂O₇ and β-M₂P₂O₇ phases (low and high temperature, respectively).⁴ Generally, the α-phase is the stable phase of Cu₂P₂O₇ at room temperature. The α-Cu₂P₂O₇ phase exhibits the monoclinic space group, C2/c, with lattice parameters of a = 6.876 Å, b = 8.113 Å, c = 9.162 Å, and β = 109.54°. High temperature analysis shows that the monoclinic C2/c transforms to monoclinic C2/m (β-Cu₂P₂O₇ phase), with lattice parameters of a = 6.827 Å, b = 8.118 Å, c = 4.576 Å, and β = 108.85°. The transition temperature of α → β phase is about 100 °C.⁵ Regarding the Zn₂P₂O₇ structure, α-Zn₂P₂O₇ has the monoclinic space group, I2/c, at room temperature, with unit cell parameters of a = 20.068 Å, b = 8.259 Å, c = 9.099 Å, and β = 106.35°. The transition temperature of α-Zn₂P₂O₇ to β-Zn₂P₂O₇ was found to be about 130 °C. The β-Zn₂P₂O₇ phase displays the monoclinic space group, C2/m, with unit cell parameters of a = 6.61 Å, b = 8.29 Å, c = 4.51 Å, and β = 105.4°.⁶ In addition, the crystal structure of Zn₂P₂O₇ was observed in other phases, such as x and y, which are metastable phases in the form of 2ZnO·P₂O₅.⁷ The δ-Zn₂P₂O₇ phase is poorly crystalline, and the γ-Zn₂P₂O₇ phase is orthorhombic with a unit cell of a = 4.950 Å, b = 13.335 Å, and c = 16.482 Å. It is interesting to note that the β-Zn₂P₂O₇ and β-Cu₂P₂O₇ phases have the same space group in the monoclinic phase, which enables the high possibility of solid solution formation at high temperature.

A group of metal pyrophosphate compounds can be applied widely in, for example, biomedical cements, chelating agents, corrosion-resistant coatings, high-quality fertilizers, glass ceramics, and microwave dielectric materials.^8–10 Most research studies on this group of compounds often focus on synthesis and characterization,^11,12 such as synthesis through wet chemical processing via metal ammonium phosphate hydrates (MNH₄PO₄·nH₂O) or metal hydrogen phosphate hydrates (MHPO₄·nH₂O) with calcination at different temperatures^2,12 as follows:

The kinetics and thermodynamics of phase formation were studied in order to explain the mechanism of the reaction, intermediate reaction, and energy of the reaction (ΔH*, ΔS*, and ΔG*, respectively).^13–15 In order to understand the crystal structure^5,6 and its properties,^16,17 structural refinement of the final product was analyzed. However, the study of the relationship between the crystal structure and properties has not been widely performed. Therefore, this research aimed to study the relationship between the crystal structure and dielectric properties, and that between the crystal structure and optical properties of the binary metal pyrophosphates, Cu_(2−x)Zn_xP₂O₇; x = 0.50–1.50, by using Rietveld refinement analysis and the extended X-ray absorption fine structure (EXAFS) fitting technique. Previously, Kim et al.¹⁸ reported two important factors which caused polarization in the structure of metal pyrophosphate compounds. These factors consisted of shifting O atoms in the collinear P–O–P bridge and movement of M²⁺ ions in the octahedral MO₆, but with relatively few details of the structure. Consequently, the effect of bond length, bond angle, bond strength, number of P–O–P clusters, average bond length, and distortion of the octahedral MO₆ site were considered in order to explain the relationship between the crystal structure, dielectric properties, and optical properties of Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00 metal pyrophosphate compounds, which produced the mechanism of the phase formation.¹⁹

2. Experimental procedure

Powders with the compositions, Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00, were synthesized via solid state reaction using the reagent-grade metal oxides and hydrogen phosphate powders CuO (99.9%), ZnO (99.9%), and (NH₄)₂HPO₄ (99%). All of the raw materials were weighed in stoichiometric proportions and then mixed homogeneously by vibratory ball milling with stabilized zirconia balls for 24 h in anhydrous ethanol. The dried powders were calcined in crucibles at 800 °C for 24 h, then vibratory-milled again for 2 h. After that, each calcined powder was sieved and mixed with 5 wt% polyvinyl alcohol (PVA) solution and uniaxially pressed into green disks of 10 mm diameter. The sintering temperature was varied between 700–900 °C for 24 h in order to obtain optimum sintering conditions. In order to eliminate the extrinsic factors of electrical properties such as grain size and density, ceramics with more than 95% theoretical density and near average grain size of each composition were selected for investigating the electrical properties. The vibration group of the samples was examined at room temperature using Fourier transform infrared (FT-IR) spectroscopy in the range of 3000–400 cm⁻¹, with eight scans on a Perkin-Elmer Spectrum GX spectrometer and a resolution of 4 cm⁻¹. Raman spectra were measured in the wavenumber range of 100−1600 cm⁻¹, with eight scans on a Thermo Scientific DXR Raman microscope, using the 532 nm excitation line of a He–Ne laser in order to support the identification of crystal structured ceramics. The dielectric properties were measured at 1 MHz via the use of an LCR meter (HP4284A; Hewlett-Packard, Palo Alto, CA). An image stacked SONY IMX214 CMOS sensor collected the colors of the samples, and matched them with CIE chromaticity diagrams in order to approximate the tendency of the absorption wavelength. Details of the crystal structure were studied through X-ray diffraction (XRD) of the powders, using a D8 Advanced powder diffractometer (Bruker AXS, Karlsruhe, Germany), with Cu K_α radiation (λ = 0.1546 nm); and X-ray absorption spectroscopy (XAS) was conducted on the beam line (BL8) of the National Synchrotron Research Center (Thailand). A double crystal Ge(220) was used for the EXAFS mono-chromator. X-ray absorption (XAS) spectra were collected in transmission mode at the Cu and Zn K-edge.

3. Results and discussion

Functional group analysis

FT-IR and Raman spectroscopy (Raman) are powerful methods for analyzing the chemical bonding of vibration, rotational, and other low-frequency modes in the phosphate system. M₂P₂O₇ has a monoclinic structure with zone-center (C-point) phonons in the lattice vibration of these metal pyrophosphates, and it can be characterized by irreducible representation of the spectroscopic group, C_2h. Factor group analysis was conducted by using the procedure of Kroumova et al.²⁰ The single metal pyrophosphate, α-Cu₂P₂O₇ (x = 0.00), showed four formula units in the unit cell (Z = 4). Cu and P atoms were attributed to the 8f position, and O atoms to both the 8f and 4e positions (Wyckoff notation). In order to remove the 3 acoustic modes (Γ_acoustic = A_u + 2B_u) from the total number (N_tot = 66) of vibrations, the optical modes of the lattice vibration were represented by

Γ_optic = 16A_g + 15A_u + 17B_g + 15B_u

The odd (un-gerade; A_u and B_u) vibration represents infrared-active modes (Γ_IR), as presented in the following equation:

Γ_IR = 15A_u + 15B_u

In addition, all even (gerade; A_g and B_g) vibrations are in Raman-active modes (Γ_Raman), as exhibited in the following equation:

Γ_Raman = 16A_g + 17B_g

The binary metal pyrophosphates, Cu_(2−x)Zn_xP₂O₇; x = 0.50, 1.00, and 1.50, showed two formula units in the unit cell (Z = 2). The Cu and Zn atoms are distributed in the 4h position, and P atoms are attributed to the 4i position. The O atoms are attributed to three positions that include 2a, 4i, and 8j. IR-active and Raman-active modes, but not acoustic modes, are shown in the following equations:

Γ_IR = 6A_u + 9B_u

Γ_Raman = 8A_g + 7B_g

In addition, the single metal pyrophosphate, α-Zn₂P₂O₇ (x = 2.00), exhibited twelve formula units in the unit cell (Z = 12) that were quite complex in structure. Zn and P atoms were attributed to the 8f position, and O atoms to both the 8f and 4e positions. IR-active and Raman-active modes, but not acoustic modes, are determined by the following equations:

Γ_IR = 48A_u + 48B_u

Γ_Raman = 49A_g + 50B_g

As a result, the number of peaks appeared to be greater in both the FT-IR and Raman spectra of α-Zn₂P₂O₇ than in other compounds. A number of peaks were detected using the Raman and IR techniques that related to the symmetry of the crystal structure in the pyrophosphate form. This resulted in the absorption of different resonant frequencies from the frequency of the absorbed radiation, which matches the transition of the energy in the vibrating bond or group. It can be proposed that bonding in the structure is different, as it appears in many of the peaks. The FT-IR spectra of the samples, which closely resemble those of the M₂P₂O₇ pyrophosphate compounds (M = Cu, Cd, Fe, Mn, Ni), are shown in Fig. 1.^1,21 The strong vibration bands at about 1190 and 1060 cm⁻¹ are attributed to asymmetric (ν_as PO₃). Vibration bands at about 1100 cm⁻¹ are attributed to symmetric stretching (ν_s PO₃) of the PO₃ unit, while asymmetric (δ_as PO₃) and symmetric (δ_s PO₃) bending vibrations are observed at about 584 and 542 cm⁻¹, respectively. The asymmetric (ν_as P–O–P) and symmetric stretch (ν_s P–O–P) bridge vibrations for this sample are observed at about 960 and 740 cm⁻¹, respectively. PO₃ determination, the rocking mode of the P–O–P deformations, and the torsional and external modes are found in the 400 cm⁻¹ region. The number of bands in this spectral region confirms the existence of distinct nonequivalent phosphate units in each structure and loss of degeneracy in the vibration modes, which were confirmed using factor group analysis.^22,23 Additionally, a strong (ν_s P–O–P) band (730 cm⁻¹) was seen in the FT-IR spectrum of the samples, and is known to be the most striking feature of polyphosphate spectra. Most of the FT-IR data showed details of the functional group of the phosphates. Therefore, the support of Raman spectroscopy was used to analyze the metal oxide stretching (M–O) and the phase-characteristics (α-, β-phase) of the pyrophosphate compounds at low frequencies. The Raman spectra of the samples are shown in Fig. 2 and tabulated in Table 1, the result corresponds well with the FT-IR result. Furthermore, the Raman results show a β-phase form in the pyrophosphate groups²⁴ through a detectably weak peak at approximately 1210 cm⁻¹. The single metal pyrophosphates (x = 0.00 and x = 2.00), and three distinct peaks that originate from the ν_as(PO₃) vibrations, are visible at about 1210, 1140 and 1080 cm⁻¹. The peaks remain at 1140 and 1080 cm⁻¹ in the samples with x = 0.50, 1.00, and 1.50, or binary metal pyrophosphates, but the peak at 1210 cm⁻¹ disappears. This indicates that the binary metal phosphates closely resemble the β-Cu₂P₂O phase, with a monoclinic structure and the space group, C2/m. In addition, single metal pyrophosphates exhibited an alpha phase (α-phase). The Cu²⁺ ion is replaced by Zn²⁺ in the Cu_(2−x)Zn_(x)P₂O₇ structure. The M–O stretching band at around 200 cm⁻¹ shifts to a lower wavenumber, and the interatomic distance between the metal and oxygen atom affects the bond strength and absorbs energy also at a lower wavenumber. The single metal pyrophosphates were observed with M–O stretching and peak splitting at 208, 212, and 248 cm⁻¹ for x = 0.00. The spectrum of the sample with x = 2.00 was observed to have five splitting peaks at 171, 182, 201, 211, and 254 cm⁻¹. These results show that the crystal structure of the sample with x = 2.00 has a lower symmetry than that of x = 0.00, due to the number of splitting peaks, which causes a different M–O bond length. Regarding binary metal pyrophosphates, splitting peaks were detected in only two regions in each of three samples: 197 and 208 cm⁻¹ for x = 0.50, 188 and 207 cm⁻¹ for x = 1.00, and 181 and 206 cm⁻¹ for x = 1.50. It should be pointed out that the crystal structure of the binary metal pyrophosphates has higher symmetry than the single metal pyrophosphate compound, which is proven using the structural analysis from Rietveld refinement and EXASF fitting.

Fig. 1 FT-IR spectra of Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00.

Fig. 2 Raman spectra of Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00.

Table 1 Vibrational assignment of the samples^a

Wavenumber (cm^−1)	FT-IR	Raman	Assignment
a vw: very weak, w: weak, m: medium, s: strong, vs: very strong.
1250–1200	—	w	α-Phase characteristic
1200–1100	vs	vs	νas(PO3)
1100–1050	vs	vs	νs(PO3)
1050–1000	vs	vs	νas(PO3)
980–950	s	vw	νas(POP)
760–730	m	w	νs(POP)
650–280	s	s	δ(OPO) + ν(M–O)
160–260	—	w	ν(M–O)
200–100	—	m	Lattice vibration

---

Dielectric and optical properties

The mean static atomic dielectric constants of the Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00 compounds were estimated using the well-known Clausius–Mossotti equation:²⁵
where ε_r is the mean static atomic dielectric constant, α_D is the sum of the dielectric polarizabilities of the individual ions, and V_m is the molar volume. The dielectric constant as a function of the composition x is presented in Fig. 3, which shows the comparison between calculated data (red bars), and measured results (green bars). The single metal pyrophosphates show a dielectric constant (ε_r) of about 13, which is higher than the ε_r of 10 in binary metal pyrophosphates. The Clausius–Mossotti equation focuses on only the dielectric constant from atomic polarization (electron cloud bias in the electric field). Indeed, the samples were measured at a frequency of 1 MHz for the decreasing extrinsic factor, and the polarization caused the cations (Cu²⁺, Zn²⁺, and P⁵⁺) and anions (O²⁻) in the structure to move. The moving ions in the electric field are the cause of the increased dielectric constant compared to the calculated data using the Clausius–Mossotti equation, as considered in this study using the bond angle, bond length, and volume of the octahedral MO₆.

Fig. 3 Dielectric constant plots of Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00.

The coordination complexes have color properties such as green for [CoF₆]³⁻, red for [Co(NH₃)₅H₂O]³⁺, and blue for [Cu(NH₃)₄(H₂O)₂]²⁺. The phenomenon of color is explained by crystal field theory (CFT),^26,27 from which Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00 compounds show a greenish color, except for the composition with x = 2.00, which exhibits a colorless powder. The optical properties and corresponding CIE chromatic coordinates^26,28,29 of these samples are shown in Fig. 4. The results of the composition with x = 0.00, illustrated a yellowish-green color, while the binary metal compounds (x = 0.50–1.50) presented color tones that changed from bluish-green to green. The composition with x = 2.00, was seen as colorless. The CIE chromaticity diagram can approximate roughly a visible and an absorption wavelength (nm). The CIE chromaticity coordinates of Cu_(2−x)Zn_xP₂O₇; x = 0.50–1.50 shift from (0.303, 0.366) to (0.292, 0.388) with increasing x, which corresponds to the visible wavelength and shifts from about 506 to 512 nm. The coordinates of α-Cu₂P₂O₇ are (0.3454, 0.4081), which corresponds to a wavelength of about 561 nm. This leads to an octahedral crystal field splitting energy (Δ_o) that illustrates z-axis expansion of the octahedral site, with its length calculated using Rietveld refinement analysis and the EXAFS fitting technique.

Fig. 4 CIE chromatic coordinates of Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00.

Structural analysis

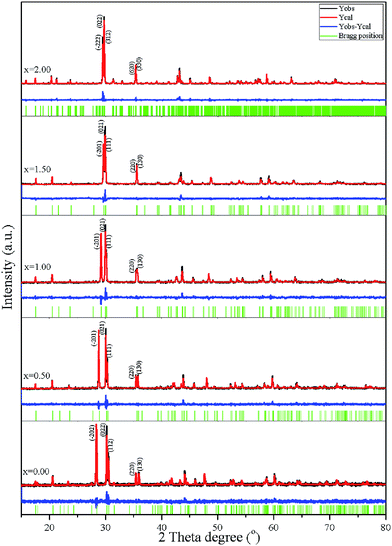
Structural refinement was performed through Rietveld refinement analysis³⁰ using the FULLPROF package.³¹ A pseudo-Voigt shape function was adequate at all times for obtaining good fits for the experimental data. The initial model was taken from parameters in the research of Calvo.³² Factors for the P–O–P bond angle, M–O bond length, and quality of fit (χ²) were obtained from the Rietveld refinement analysis and are summarized in Table 2. Fig. 5 shows the calculated (Y_cal) and observed (Y_obs) diffraction patterns and different (Y_obs − Y_cal) peaks of the samples. The refinement plot gives the evolution of the X-ray diffraction (XRD) patterns in the various Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00 compositions, and their synthesized pyrophosphates show that single-phase compounds constitute solid solutions. Similarity in the XRD patterns (peak positions) is an indication of only small variations in the unit cell parameters, for example, the small difference in size between the Cu²⁺ ion (R = 0.73 Å) and Zn²⁺ ion (R = 0.74 Å).³³ Data collected from the Rietveld refinement analysis and the XRD of the powders confirmed the monoclinic system for the metal pyrophosphate compounds, Cu_(2−x)Zn_(x)P₂O₇; x = 0.00 (space group C2/c (15), Z = 4), x = 0.50–1.00 (space group C2/m (12), Z = 2), and x = 2.00 (space group I2/c (15), Z = 12). The relationship between the reflection planes (hkl) of α-Zn₂P₂O₇, α-Cu₂P₂O₇, and Cu_(2−x)Zn_xP₂O₇; x = 0.50–1.50 in Fig. 5 projects the lattice size. The results show that the crystal structure size of the binary metal pyrophosphates is smaller than that of single metal pyrophosphates. Also, the long range ordering of the binary metal pyrophosphates is wider than that for single metal pyrophosphates, which was considered to be the (111) plane of Cu_(2−x)Zn_xP₂O₇; x = 0.50–1.50, the (112) plane of α-Cu₂P₂O₇, and the (312) plane of α-Zn₂P₂O₇. Furthermore, the refined data showed that the space group of Cu₂P₂O₇ had increased ordering the monoclinic system with C2/c to that with C2/m, when Cu²⁺ was replaced by Zn²⁺ in the pyrophosphate structure. The final refinement demonstrated the P–O–P bridge and asymmetry of the octahedral MO₆. Furthermore, the P–O–P bond angle was expanded from 155° to 180°. The calculated number of P–O–P clusters decreased from 4 to 2 clusters per unit cell, and the number of octahedral MO₆ sites decreased from 8 to 4 sites per unit cell, due to the increased long range ordering and decreased number of unit cells, which had a direct effect on the electrical properties of the matter. The changing M–O bond length in the binary metal pyrophosphates was exhibited through the color of the matter, which resulted from the changing crystal field splitting²⁶ in the 3d⁹-orbital Cu²⁺ ion, and this was observed in Raman spectroscopy. The relationship between the M–O bond length and Raman shift is tabulated in Table 3. The Cu²⁺ ion was replaced by Zn²⁺ in Cu_(2−x)Zn_(x)P₂O₇, which appeared in the M–O stretching band at around 210 cm⁻¹. The stretching band shifted to a lower wavenumber, due to the increased interatomic distance between the metal and oxygen atom, thus affecting the bond strength and energy absorbance. Table 3 shows the band position of the M–O bond stretching compared with Rietveld refinement results and an approximation of the calculated frequencies using a fundamental equation. This analysis focused on the tendency of the Raman band shift; therefore, the factors used in the calculation contained only the atomic mass. The results of the calculations were obtained in k terms. Each M–O bond absorbs energy at a different frequency, which brings about a peak in a different position in the Raman shift. The close M–O bond lengths exhibited close peak positions and this developed into an observation band. Thus, the close M–O bond lengths are grouped in Fig. 6, with the number of groups corresponding to that of the band in the Raman. All of the results are consistent with compositions with increasing x that correspond to a decreasing average M–O bond length and decreasing observation frequencies in both the Raman shift and fundamental frequency calculation. In addition, the crystal structure and bonding character of the materials were considered. The average bond strength (〈S_P–O〉) of P⁵⁺ and O²⁻ in the [O3P–O–PO3]⁴⁻ or [P₂O₇]⁴⁻ cluster and the bond valence sum (〈V_P–O〉) were calculated according to the procedure reported by Brown.³⁴ The average bond strength (Table 3) can be estimated from the average sum of the bond valence divided by the average cation coordination numbers, from which the bond valence can be defined by
where R is the length of a bond between P and O atoms. R₀ and B are parameters determined empirically, by which the B parameter must use a universal value for the empirical parameter B; B = 0.37 Å, which makes a one-parameter model relating to the formal valence V, bond length R, and coordination number N. Therefore, the sum of the bond valence is defined by

Table 2 Bond angle and bond length from Rietveld refinement for the samples

Sample		x = 0.00	x = 0.50	x = 1.00	x = 1.50	x = 2.00
POP angle (°)		154.6 (10)	180.0 (11)	180.0 (11)	180.0 (11)	138.00 (30)	159.00 (30)
M–O bond length (Å)	M–O1	1.980 (5)	2.016 (2)	2.037 (6)	2.047 (7)	3.135 (15)	2.196 (11)	1.976 (11)
	M–O2	1.942 (6)	1.971 (4)	2.012 (5)	1.999 (2)	1.997 (13)	2.017 (11)	2.010 (12)
	M–O3	1.886 (5)	2.540 (2)	2.476 (3)	2.422 (3)	2.052 (13)	2.371 (16)	1.920 (11)
	M–O3	2.920 (9)	2.540 (2)	2.476 (3)	2.422 (3)	2.181 (15)	2.079 (11)	2.102 (14)
Space group		C2/c	C2/m	C2/m	C2/m		I2/c
Z		4	2	2	2		12
χ^2		1.21	1.21	1.33	1.58		1.6
Lattice parameter	a (Å)	6.8811 (4)	6.7904 (3)	6.7257 (3)	6.6672 (4)		20.1098 (6)
	b (Å)	8.1173 (4)	8.1576 (3)	8.1986 (3)	8.2413 (4)		8.2732 (2)
	c (Å)	9.1614 (5)	4.5579 (2)	4.54312 (3)	4.5307 (3)		9.1067 (3)
	β (°)	109.523 (3)	108.429 (2)	107.464 (3)	106.473 (3)		106.326 (2)
	V (Å^3)	482.308 (43)	239.538 (17)	238.971 (24)	238.733 (27)		1454.012 (74)
R-factor (%)	Rp	9.27	10.0	11.50	14.20		15.70
	Rwp	11.70	12.70	14.40	17.90		23.10
	Rexp	10.68	11.57	13.49	14.43		18.27

---

Fig. 5 Rietveld refinement patterns of Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00.

Table 3 The approximate grouping of M–O bonding and bond strength of samples^a,b

Composition	Observed	(1)	(2)	(3)	(4)	(5)
a Ra: Raman shift (cm^−1).b Avg D: average atomic distance (Å).
x = 0.00	Ra (cm^−1)	—	—	208	212	248
	Avg D (Å)	—	—	1.886	1.961	2.92
	Cal.			203.72k
	〈SP–O〉			1.1232
x = 0.50	Ra (cm^−1)	—	197	208	—	—
	Avg D (Å)	—	1.994	2.54	—	—
	Cal.			203.57k
	〈SP–O〉			1.2840
x = 1.00	Ra (cm^−1)	—	188	207	—	—
	Avg D (Å)	—	2.024	2.476	—	—
	Cal.			203.42k
	〈SP–O〉			1.2938
x = 1.50	Ra (cm^−1)	—	181	206	—	—
	Avg D (Å)	—	2.023	2.422	—	—
	Cal.			203.28k
	〈SP–O〉			1.3011
x = 2.00	Ra (cm^−1)	171	182	201	211	254
	Avg D (Å)	1.976	2.033	2.188	2.371	3.135
	Cal.			203.14k
	〈SP–O〉			1.0969

---

Fig. 6 The approximate grouping of the M–O bonding of Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00.

In divergence, the average bond strength of a single metal pyrophosphate is lower than that in binary metal pyrophosphates. Bond energies and force constants decrease with average bond strength. Determination of a quantitative correlation with the same type of bonding is complex.³⁵ The EXAFS fitting technique was used in support of the structural refinement analysis.

The EXAFS spectra of the samples for the Cu K-edge and Zn K-edge are shown in Fig. 7a and b, respectively. In order to study the environment around the Cu atoms, a primitive EXAFS model was taken from parameters obtained from the Rietveld refinement of each sample. The details of the EXAFS spectroscopic fitting are summarized in Table 4. The results exhibited distortion of the octahedral CuO₆. The sample with x = 0.00 showed three main shells, of which the first shell of the spectrum was modeled in consistency with four oxygen atoms that had interatomic distances of 1.9050 Å and 1.9643 Å for Cu–O1 and Cu–O2, respectively. Then, the second shell detected only one oxygen atom; Cu–O3, which had an interatomic distance of 2.3001 Å. The last shell detected the oxygen atom of octahedral CuO₆, which had an interatomic distance of 2.9136 Å that combined scattering from a phosphorus atom, Cu–P bond and copper metal atom, as well as a Cu–M interaction. In the case of the binary metal pyrophosphate samples (x = 0.50–1.50), the Cu–O3 interatomic distances shortened, and were included in the second shell. As a result, the second shell intensity of the binary metal pyrophosphate samples was seen to be higher than that in Cu₂P₂O₇ (x = 0.00). The addition of a fourth shell did not improve the quality of fit, and fitting of the Zn K-edge EXAFS was related to that of the Cu K-edge, with the curve shifting to a high radial distance due to a larger atomic radius. The EXAFS spectrum of Zn–O is shown by a single oscillation from four oxygen atoms surrounding the central Zn atom in the first shell, while Zn consists of two oxygen atoms in the second shell. The next shell described the combination of Cu–M (M = Cu/Zn), and the Cu–P interaction. The difference in radial distances between the Rietveld refinement and EXAFS fitting may be caused by the type of measurement in each technique, in which X-ray diffraction was used to investigate the global structure, and X-ray absorption was used to probe the details of the Cu/Zn local structure.^36,37 The fitting statistic (R-factor) of the Zn K-edge is worse than that of the Cu K-edge because of two factors. Firstly, the crystal structure of α-Zn₂P₂O₇ showed lower symmetry when compared with other samples, and the Zn exhibited three different types of atomic position in the unit cell. Secondly, there was a limitation of the instrument, in which the absorption edge of Zn (9659 eV) approached the maximum energy range (1250–10 000 eV) of the BL8 station.

Fig. 7 EXAFS fitting curves of Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00.

Table 4 Bond length from EXAFS fitting for the samples

Composition (x)	Path	Shell	CN	R (Å)	σ^2 (Å^2)	R-factor
0.00	Cu–O1	1	2	1.90505	0.00508	0.00369
	Cu–O2	1	2	1.96427	0.00499
	Cu–O3	2	1	2.30075	0.03223
	Cu–O3	3	1	2.91358	0.00796
0.50	Cu–O1	1	2	1.93460	0.00775	0.00519
	Cu–O2	1	2	1.97180	0.00996
	Cu–O3	2	2	2.32395	0.02004
	Zn–O1	1	2	1.98304	0.02336	0.01175
	Zn–O2	1	2	2.02117	0.00034
	Zn–O3	2	2	2.38214	0.03426
1.00	Cu–O1	1	2	1.93087	0.00575	0.00514
	Cu–O2	1	2	1.97205	0.00647
	Cu–O3	2	2	2.28269	0.02209
	Zn–O1	1	2	1.98889	0.02117	0.01085
	Zn–O2	1	2	2.03131	0.00406
	Zn–O3	2	2	2.35128	0.07393
1.50	Cu–O1	1	2	1.94951	0.00611	0.00763
	Cu–O2	1	2	1.99453	0.25154
	Cu–O3	2	2	2.26768	0.0392
	Zn–O1	1	2	2.00714	0.01068	0.00393
	Zn–O2	1	2	2.05349	0.01074
	Zn–O3	2	2	2.33473	0.04422
2.00	Zn–O1	1	2	1.96928	0.00176	0.02072
	Zn–O2	1	2	2.05357	0.00823
	Zn–O3	2	1	2.11171	0.00931
	Zn–O3	3	1	2.58544	0.06587

---

The refinement results from P–O–P bond angles can be classified into two groups. The first group includes a P–O–P bond angle of less than 180° such as the compositions with x = 0.00 and x = 2.00, or single metal pyrophosphates. The sample with x = 0.00 had a P–O–P bond angle of 154.6°, and appeared with 4 clusters per unit cell and symmetric P–O bond lengths of 1.574 Å. The composition with x = 2.00 showed two different P–O–P bond angles, including 159.0°, which appeared with 8 clusters per unit cell and asymmetric P–O bond lengths of 1.770 Å and 1.390 Å, and the P–O–P bond angle of 138.0° appeared with 4 clusters per unit cell and a symmetric P–O bond length of 1.640 Å. The second group had a P–O–P bond angle equal to 180°, which contained the compositions with x = 0.50, 1.00, and 1.50, or binary metal pyrophosphates. All of the compositions in this group exhibited a P–O–P bond angle equal to 180.0° and appeared with 4 clusters per unit cell and symmetric P–O bond lengths of 1.524 Å, 1.521 Å, and 1.519 Å for x = 0.50, 1.00, and 1.50, respectively. However, when compared to an equal space volume, the number of P–O–P clusters in each composition was equal. As a result, the number of P–O–P clusters did not affect the polarization of the samples. The single metal pyrophosphates showed outstanding dielectric constants, while all of the binary metal pyrophosphates presented lower and similar dielectric constants. It was highly possible that high polarization caused a narrow P–O–P bond angle, as analyzed through the dielectric constants of the metal pyrophosphate compounds. In addition, the long P–O bond length of x = 2.00 (weak bonding) led to the better polarization of x = 0.00, 0.50, 1.00, and 1.50. The binary metal pyrophosphates (x = 0.50, 1.00, and 1.50) exhibited a similar dielectric constant, due to all of the P–O–P bond angles being equal. However, the dielectric constant tends to decrease slightly when the component x increases. Results from the final refinement showed decreasing average M–O bond lengths in the octahedral MO₆ site, of which short length bonding caused hard polarization. Additionally, the volume of selected octahedral coordinations was calculated using the method reported by Swanson et al.³⁸ for highlighting the relationship between the polarization and metal oxide bonding. Besides, the distortion index (D) was used to describe the distortion of the structure. Baur³⁹ described D based on bond lengths in the distortion index as

where l_av is the average bond length, and l_i is the atomic distance from the central atom to the ith coordinating atom. These results are tabulated in Table 5. All of the data showed decreasing average bond lengths, octahedral volume and distortion index, which exhibited decreasing polarization (dielectric constant, ε_r) when the component x increased. These analyses show that polarization of the Cu_(2−x)Zn_xP₂O₇; x = 0.00–2.00 system occurred due to two factors, with shifting O atoms in the collinear P–O–P bridge probably being the main factor in a narrow bond angle that causes high polarization and a high dielectric constant. The movement of M²⁺ ions in the octahedral MO₆ is a supplementary factor, in which the longer average M–O bond length and larger octahedral volume lead to high polarization and the high dielectric constants of metal pyrophosphate compounds.

Table 5 The evolution of average bond length, octahedral volume, and distortion index of the samples

Composition (x)	Average bond length (Å)	Octahedral volume (Å^3)	Distortion index
0.50	2.1758	12.6629	0.1117
1.00	2.1720	12.5791	0.0935
1.50	2.1659	12.4106	0.0821

---

The distortion of octahedral CuO₆ exhibited decreasing Cu–O3 bond lengths in going from x = 0.00 to 1.50, which corresponded to a decreasing octahedral crystal field splitting energy (Δ_o) (Table 6). As a result, Zn²⁺ increased this value when the Cu²⁺ in the Cu₂P₂O₇ compound was replaced. The color of the compounds illustrated that its hue changes from bluish-green to green. The colorless composition, when x = 2.00 or Zn₂P₂O₇, caused a state of fulfillment in the octet rule of the Zn²⁺ ions ([Ar] 3d¹⁰) in the structure, despite distortion appearing in the octahedral ZnO₆ site. The octahedral splitting diagram of Cu_(2−x)Zn_xP₂O₇; x = 0.00–1.50 is shown and summarized in Fig. 8. Total interpretations showed that a distorted octahedral MO₆ affects both the color of the matter and the polarization of the octahedral unit, as reflected by the dielectric constant.

Fig. 8 Summary of the crystal field splitting in Cu_(2−x)Zn_xP₂O₇; x = 0.00–1.50.

Table 6 Approximate wavelength of the energy absorption

Composition (x)	Wavelength (nm)		Δo (kJ mol^−1)	Cu–O3 (Å) bond length
	Observed	Absorbed		XRD	EXAFS
0.00	561	403	297	2.92	2.91
0.50	506	660	181	2.54	2.32
1.00	508	665	180	2.48	2.28
1.50	512	675	177	2.42	2.27
2.00	—	—	—	—	—

---

4. Conclusion

The single metal pyrophosphates, α-Cu₂P₂O₇ and α-Zn₂P₂O₇, and binary metal pyrophosphates, Cu_(2−x)Zn_xP₂O₇; x = 0.00–1.50, were synthesized successfully via solid state reaction from metal oxides and ammonium hydrogen phosphate. All of the samples exhibited a single-phase monoclinic system with the C2/c space group for α-Cu₂P₂O₇ and α-Zn₂P₂O₇ (I2/c), and the C2/m space group for the binary metal pyrophosphates, which showed that the binary metal pyrophosphates had more structural symmetry than the single metal pyrophosphates. Rietveld refinement and EXAFS fitting data presented the P–O–P bond angle and P–O bond length in the P₂O₇⁴⁻ ions, and also details of the octahedral MO₆ including the average bond length, octahedral volume, and distortion index. The addition of Zn²⁺ ions in the Cu₂P₂O₇ structure caused distortion of the crystal structure, which led to a change in the bond length and bond angle of the P–O–P clusters in the P₂O₇⁴⁻ ions, and changed the octahedral volume and average bond lengths of the octahedral MO₆ site. Shifting O atoms in the collinear P–O–P bridge is probably the main factor in ionic polarization, in which a narrow bond angle caused high polarization and high dielectric constants. The movement of M²⁺ ions in octahedral MO₆ is a supplementary factor, in which the longer average M–O bond length and larger octahedral volume led to the high polarization and high dielectric constants of metal pyrophosphate compounds. The color of the samples changed from bluish-green to green when the Zn component increased because the absorption wavelength increased and corresponded to the decrease in z-axis expansion. The final results showed that the distortion of the octahedral MO₆ caused a direct effect on the color of the metal pyrophosphate compounds, while the change of the P–O–P bridge affected the dielectric properties.

Acknowledgements

This work was supported by the Thailand Research Fund (TRF) under the TRF Senior Research Scholar, Grant no. RTA5680008 and The National Nanotechnology Center (NANOTEC), NSTDA, Ministry of Science and Technology, Thailand, through its program of Center of Excellence Network. The authors also would like to thank the Synchrotron Light Research Institute (Public Organization) for the XAS measurements.

References

1. E. Steger and B. Käßner, Spectrochim. Acta, Part A, 1968, 24, 447–456.
2. B. Boonchom and R. Baitahe, Mater. Lett., 2009, 63, 2218–2220.
3. M. Weil and B. Stöger, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 603–614.
4. A. Durif, Crystal chemistry of condensed phosphates, Plenum Press, New York, 1995.
5. B. E. Robertson and C. Calvo, Acta Crystallogr., 1967, 22, 665–672.
6. C. Calvo, Can. J. Chem., 1965, 43, 1147–1153.
7. M. A. Petrova, V. I. Shitova, G. A. Mikirticheva, V. F. Popova and A. E. Malshikov, J. Solid State Chem., 1995, 119, 219–223.
8. J. I. Bian, D. W. Kim and K. S. Hong, Jpn. J. Appl. Phys., Part 1, 2004, 43, 3521–3525.
9. J. J. Bian, D. Kim and K. S. Hong, J. Mater. Sci., 2005, 40, 1801–1803.
10. W. Wenwei, F. Yanjin, W. Xuehang, L. Sen and L. Shushu, J. Phys. Chem. Solids, 2009, 70, 584–587.
11. Z. W. Xiao, G. R. Hu, Z. D. Peng, K. Du and X. G. Gao, Chin. Chem. Lett., 2007, 18, 1525–1527.
12. A. Bensalem, M. Ahluwalia, T. V. Vijayaraghavan and Y. H. Ko, Mater. Res. Bull., 1997, 32, 1473–1483.
13. D. Brandová, M. Trojan, M. Arnold, F. Paulik and J. Paulik, J. Therm. Anal., 1988, 34, 1449–1454.
14. D. Brandová, M. Trojan, F. Paulik and J. Paulik, J. Therm. Anal., 1987, 32, 1923–1928.
15. B. Boonchom, R. Baitahe, S. Kongtaweelert and N. Vittayakorn, Ind. Eng. Chem. Res., 2010, 49, 3571–3576.
16. A. Jouini, J. C. Gâcon, M. Ferid and M. Trabelsi-Ayadi, Opt. Mater., 2003, 24, 175–180.
17. T. Yang and J. Lin, J. Solid State Chem., 2013, 198, 1–5.
18. C. H. Kim and H. S. Yim, Solid State Commun., 1999, 110, 137–142.
19. R. Baitahe and N. Vittayakorn, Thermochim. Acta, 2014, 596, 21–28.
20. E. Kroumova, M. I. Aroyo, J. M. Perez-Mato, A. Kirov, C. Capillas, S. Ivantchev and H. Wondratschek, Phase Transitions, 2003, 76, 155–170.
21. B. Boonchom and N. Phuvongpha, Mater. Lett., 2009, 63, 1709–1711.
22. O. Pawlig and R. Trettin, Mater. Res. Bull., 1999, 34, 1959–1966.
23. O. Pawlig, V. Schellenschläger, H. D. Lutz and R. Trettin, Spectrochim. Acta, Part A, 2001, 57, 581–590.
24. K. Pogorzelec-Glaser, A. Pietraszko, B. Hilczer and M. Polomska, Phase Transitions, 2006, 79, 535–544.
25. M. T. Sebastian, Dielectric materials for wireless communication, Elsevier, Amsterdam, Boston, 2008.
26. A. El Jazouli, B. Tbib, A. Demourgues and M. Gaudon, Dyes Pigm., 2014, 104, 67–74.
27. L.-T. Chen, C.-S. Hwang, I. L. Sun and I.-G. Chen, J. Lumin., 2006, 118, 12–20.
28. B. Kukliński, D. Wileńska, S. Mahlik, K. Szczodrowski, M. Grinberg and A. M. Kłonkowski, Opt. Mater., 2014, 36, 633–638.
29. B.-K. Kim and R.-H. Park, Image and Vision Computing, 2010, 28, 952–964.
30. H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71.
31. J. Rodríguez-Carvajal, Physica B: Condensed Matter, 1993, 192, 55–69.
32. B. E. Robertson and C. Calvo, Can. J. Chem., 1968, 46, 605–612.
33. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
34. I. Brown, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1977, 33, 1305–1310.
35. I. Brown, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1992, 48, 553–572.
36. V. I. Voronin, I. F. Berger, V. A. Cherepanov, L. Y. Gavrilova, A. N. Petrov, A. I. Ancharov, B. P. Tolochko and S. G. Nikitenko, Nucl. Instrum. Methods Phys. Res., Sect. A, 2001, 470, 202–209.
37. L. Yingjie, B. Huliyageqi, W. Haschaolu, Z. Song, O. Tegus and I. Nakai, J. Electron Spectrosc. Relat. Phenom., 2014, 196, 104–109.
38. D. K. Swanson and R. C. Peterson, Can. Mineral., 1980, 18, 153–156.
39. W. Baur, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 1195–1215.

---