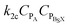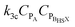Chain growth polymerization mechanism in polyurethane-forming reactions

Abstract

The reaction of polyol and isocyanate monomers to form polyurethanes is commonly presented in reaction chemistry that implies a step-growth mechanism for the polymerization. However, viscosity versus temperature profiles of both experimental studies and gel-forming simulation studies indicate that the degree of polymerization resulting from the reactions varies considerably from reactions with catalysts compared with those without catalysts. An extension of a simulation based solely on step-growth mechanisms to simulations that include chain growth via an active catalytic complex provides viscosity and temperature profiles that are consistent with the range of experimental data. The results indicate that as catalytic mechanisms dominate the kinetics chain growth mechanisms also overwhelm step growth mechanisms. Based on this mechanism, the choice of catalysts can impact both the rate of reaction and degree of polymerization length; both being of high importance in engineering urethane foams.

---

Introduction

Polyurethane polymerization is a complex thermoset process with a formulation utilizing over a dozen degrees of freedom. Formulations may be as simple as consumer spray foam canisters bought at the hardware store, to reaction injection mouldings that make complex automobile parts in a single process.^1,2,3 The kinetic parameters are affected by factors like the composition of the reaction mass, type of catalyst, and possible side reactions.⁴

Urethane is produced through alcohol–isocyanate reactions.⁵ Moieties of alcohol and isocyanate are located on monomers (initially) and polymers which are formed after the reaction has begun. In addition to alcohol isocyanate reactions, catalysts attach to and detach from moieties throughout the reaction, providing reaction sites and increasing the reaction rate.

Polyurethane polymerization and its kinetics have been studied by various researchers through chromatography, viscoelastic studies, intrinsic fluorescence, chemorheology, rheology and numerical fitting of experimental data. Based on these methods, different kinetics^6,7 and mechanisms^5–13 have been introduced for urethane reactions. However, none of them were robust enough to successfully define this complex polymerization mechanism. Generally, two different approaches have been used to describe catalysed polyurethane polymerization. One mechanism includes catalyst forming a complex with isocyanate groups which will then react with an alcohol moiety to produce urethane. This reaction is often assumed to be an intermediate or equilibrium reaction, leading to hyperbolic reaction rate expressions.^5,14 The other mechanism describes polymerization by nth order reaction rate equations for all reactions, providing parameters and good fits to the experimental data. The second approach has been used by Zhao et al. in the developments of a modelling package that is used as the starting point for the work presented in this paper.¹⁵

This paper is on the extension to the work done by Zhao et al. and Ghoreishi et al. to introduce fundamental reactions involved in association, reaction, and disassociation of catalyst complexes. It is hypothesized that the resulting series of fundamental reaction mechanisms will result in a fundamentally-correct simulation package that can span the performances from purely step-growth non-catalytic urethane-forming reactions to the “hyperbolic” catalytic behaviour mechanisms that may be more chain-growth in nature.

In this paper, the catalyst is assumed to attach to both isocyanate and alcohol monomers and then undergo polymerization reactions. The goal is to determine if a series of parallel reaction mechanisms can span the transition from step-growth to chain-growth polymerization, depending upon the formulation being simulated.

The mechanism for uncatalysed reactions is considered to be step growth polymerization with nth order reaction rate expressions.¹⁵ These homogeneous reactions are presented in Table 1. Simulation code is written in a way that it can handle up to three different polyols (monomers), therefore, reactions 4 to 9 and 13 through 19 are the same as reactions 1 to 3 and 10 to 12, respectively; the only difference is that they are written for different polyols. Reactions 21 through 34 are water–isocyanate reactions. These reactions do not affect the simulation as the experimental results are gained from Voranol 490 polyurethane gel system (no water is present gel systems).

Table 1 Homogeneous reactions describing polyurethane polymerization. A, B, P, k and C represent isocyanate, alcohol, polymer, reaction rate coefficient and concentration. Subscripts P, S, and HS stand for primary, secondary and hindered secondary alcohol moieties. k_1c, k_2c and k_3c are homogeneous reaction rate coefficients for primary alcohol with isocyanate, secondary alcohol with isocyanate and hindered-secondary alcohol with isocyanate reactions, respectively

Rxn #	Reaction	Description	Rate expression
1	A + BP → P	Monomer A + monomer B	k1hCBPCA
2	A + BS → P		k2hCBSCA
3	A + BHS → P		k3hCBHSCA
10	PA + BP → P	A on polymer + monomer B	k1hCPCBP
11	PA + BS → P		k2hCPCBS
12	PA + BHS → P		k3hCPCBHS
19	A + PBP → P	Monomer A + B on polymer	k1hCACP
20	A + PBS → P		k2hCACP
21	A + PBHS → P		k3hCACP

---

In the polyurethane polyaddition the catalyst is considered the initiator which forms a complex with isocyanate or alcohol. In the poly-addition, the catalyst forms a complex that is assumed to survive the reaction process with a transfer of location in the molecule. In reactions parallel to the addition reactions, are reactions of addition and disassociation of the catalyst to form and disassociate the complex. Once the complex has disassociated, the rate of association of the catalyst is toward association with any free reaction moiety in the reaction mix.

During polyurethane gel reactions, polymerization takes place within a matrix, inter-molecular reactions take place repeatedly and termination does not occur. However, a few monomers might stay in the solution even when the reaction is over and most of the time an initiator is needed. Also, at the beginning of the reaction, the backbone of the polymer chain increases rapidly in mass and the mass stays at the same value until the end. Based on these characteristics, it could be concluded that polyurethane polymerization does not follow a 100% step growth or a 100% chain growth mechanism. It could be considered that addition polymerization complies the most with polyurethane polymerization. Most of the modelling work reported in literature is based on step-growth polymerization, but both are reported. Bayer Co. reported producing polyurethanes by suspension polyaddition and Radhakrishnan et al. have reviewed the process.¹⁶

An artefact of chain-growth polymerization, versus step-growth, is that at the same conversion (e.g. 10% conversion of moieties) the chain-growth mechanism produces fewer polymer molecules which have higher molecular weight. This translates to chain-growth polymerization systems having higher viscosities at the same conversions.

To a first approximation, in near-adiabatic urethane gel reactions, the conversion is proportional to temperature increase as based on the assumption that the heat of reaction is approximately the same for all reacting moieties. And so, a comparison of experimental data on viscosity versus temperature (or extend of reaction) in the presence of different (or no) catalysts can be used to identify relative kinetic chain lengths of polymerization processes. If a formulation without catalyst and with different catalysts had the same viscosity versus temperature profiles it would be evidence of purely step growth mechanisms. When variations of these profiles exist, larger kinetic chain lengths and degrees of polymerization would manifest as more-rapid increases in viscosity. These trends will apply to systems where the catalysts do not impact viscosity through other mechanisms such as participating in the reactions as cross-linkers.

Modelling basis

Catalysed reactions are categorized into three groups: association to form a complex, disassociation of the complex, and propagation at the complex site. Termination does not happen in this particular system; therefore no reaction is counted as termination. All catalysed reactions used for simulation are listed in Table 2. Reaction rate constants are calculated using the Arrhenius equation. The values of pre-exponential factors and activation energies used for the reaction coefficients are based on the type of alcohol moiety (primary, secondary and hindered secondary) that reacts with an isocyanate moiety. Rate constants are independent of whether the moieties are attached to a monomer, oligomer or polymer molecule.¹⁷

Table 2 Catalysed reactions describing polyurethane polymerization. A, B, P, X and C represent isocyanate, alcohol, polymer, catalyst and concentration and subscripts P, S, and HS stand for primary, secondary and hindered secondary alcohol moieties. k_a, k_d, k_1c, k_2c and k_3c are catalytic reaction rate coefficients for attachment, disassociation, primary alcohol with isocyanate, secondary alcohol with isocyanate and hindered-secondary alcohol with isocyanate reactions, respectively

Rxn #	Category	Reaction	Rate expression
35	Catalyst + monomers association	A + X → AX	kaCACX
36		B1P + X → B1PX	kaCB1PCX
37		B1S + X → B1SX	kaCB1SCX
38		B1HS + X → B1HSX	kaCB1HSCX
39	Monomer A + monomer B propagation	A + BPX → PAX	k1cCBPXCA
40		A + BSX → PAX	k2cCBSCA
41		A + BHSX → PAX	k3cCBHSCA
42		AX + BP → PBPX	k1cCBPCAX
43		AX + BS → PBSX	k2cCBSCAX
44		AX + BHS → PBHSX	k3cCBHSCAX
45	A on polymer + monomer B propagation	PAX + BP → PBPX	k1cCPAXCBP
46		PAX + BS → PBSX	k2cCPAXCBS
47		PAX + BHS → PBHSX	k3cCPAXCBHS
48		PA + BPX → PAX	k1cCPACBPX
49		PA + BSX → PAX	k2cCPACBSX
50		PA + BHSX → PAX	k3cCPACBHSX
51	Monomer A + B on polymer propagation	AX + PBP → PBPX	k1cCAXCPBP
52		AX + PBS → PBSX	k2cCAXCPBS
53		AX + PBHS → PBHSX	k3cCAXCPBHS
54		A + PBPX → PAX
55		A + PBSX → PAX
56		A + PBHSX → PAX
57	A on polymer + B on polymer propagation	PAX + PBP → PBPX	k1cCPAXCPBP
58		PAX + PBS → PBSX	k2cCPAXCPBS
59		PAX + PBHS → PBHSX	k3cCPAXCPBHS
60		PA + PBPX → PAX
61		PA + PBSX → PAX
62		PA + PBHSX → PAX
63		PBP + PAX → PAX + X
64		PBS + PAX → PAX + X
65		PBHS + PAX → PAX + X
66	Catalyst dissociation	PAX → PA + X	kdCPAX
67		PBPX → PBP + X	kdCPAX
68		PBSX → PBS + X	kdCPAX
69		PBHSX → PBHS + X	kdCPAX
70		AX → A + X	kdCAX
71		BPX → BP + X	kdCBPX
72		BSX → BS + X	kdCBSX
73		BHSX → BHS + X	kdCBHSX
74	Catalyst + moieties association	PA + X → PAX	kaCPACX
75		PBP + X → PBPX
76		PBS + X → PBSX

---

For the elementary reactions listed in Table 2, the term “association” is used in place of initiation since the initiator is not actually destroyed. Also, the term “disassociation” is used in place of both termination and transfer since the catalyst is assumed not to terminate and since all transfer processes are assumed to go through the step of first dis-associating to the free catalyst.

Propagation by IUPAC definition is “chemical reactions between a chain carrier and a monomer that results in growth of a polymer chain and regeneration of at least one chain carrier.” In this system, isocyanate and alcohol moieties on polymer molecules react and form larger polymer molecules. The IUPAC definition does not include polymer–polymer reactions, but these reactions could be categorized under the propagation stage, as the IUPAC definition is mainly based on polymerization processes which involve two-functional monomers.

For this system, propagation takes place through reactions 39 to 65, where new chains of polymer are formed and chains that have already been formed grow longer or form branches. During propagation, active sites on the growing molecule stays intact i.e. the catalyst stays attached but may move to the adjacent moiety, instead of going to the solution.

During chain transfer, the active site on an oligomer or macromolecule is disassociated and transferred to the solution, another molecule or another site on the same molecule. Transfer reactions are reactions 66 through 73 where catalyst molecule disassociates from its complex with isocyanate or alcohol moieties and goes to the solvent.

Kinetic chain length is not often considered in the discussion of thermoset systems because the degree of polymerization is ultimately determined by cross-linking, not accounted for in traditional derivations on kinetic chain length. However, at low conversions, and especially when interpreting how different catalysts can lead to faster increases in viscosity at the same conversions, the literature theories and interpretations related to kinetic chain lengths are useful.

For chain polymerization, kinetic chain length is defined as the ratio of the rate of monomer consumption (propagation) divided by the sum of the rates of initiation and transfer.¹⁸ For this system, initiation is the formation of the reacting complex (association). Furthermore, at steady state where a catalyst forms the reacting complex, the complex's rate of association is equal to the rate of disassociation. Eqn 1 expresses this equality, where ν is the kinetic chain length, r is reaction rate, and subscripts p, a, and d stand for propagation, association, and disassociation.

However, within the limit of low polymerization at the beginning of the reaction, transfer reactions take place by the catalyst disassociating and going into the solvent. Hence, rates of disassociation and transfer would become equal and eqn (1) would simplify to eqn (2).

Under the assumptions that association is always with moieties on monomers (as opposed to on polymers) and there is no cross-linking, the kinetic chain length is the degree of polymerization. At low conversions, both cross-linking and re-attachment of catalyst to an existing polymer are low since there are no polymer molecules at the onset of the reaction.

For a simple homo-polymer reaction following the catalyst model of association (r_a = k_a[X][A]), propagation (r_p = k_p[BX][A]), and disassociation (r_d = k_d[BX]), eqn (3) emerges, where “[ ]” indicates concentrations and X, A and BX are catalyst, isocyanate and alcohol complex, respectively.

Of these, the most useful derivation is eqn (4).

The utility of eqn (4) is in evaluating trends of the simulation code, where for simulations at the same initial concentration of monomer(s) and at low conversions (e.g. <70% conversion), higher ratios of k_p/k_d will lead to higher degrees of polymerization. Preferably, the comparisons are where k_p is constant and variations in the ratio occur due to changing k_d; for comparisons under these constraints, the systems will have similar temperature and monomer concentrations as a function of time. This utility in evaluating simulation code applies to the more-complex co-polymer systems such as that described by the Table 2 reactions.

The polymer degree of polymerization, by definition, is related to both the moles of monomer that have reacted and the moles of polymer that have formed as expressed by eqn (5) on the basis of one litre (concentration in moles per litre) and constant density resin.

Eqn (5) is written for the whole urethane system and assumes no polymer present at the start of reaction. However, the simulation results show a degree of polymerization of 2 which keeps increasing incrementally until the time at which temperature profile shows an inflection point. At this point, a rapid rise is seen in the degree of polymerization profile. To overcome this problem, homogeneous and catalytic degrees of polymerization were introduced (eqn (6) and (7)), where mrc, mrh, [P]_c and [P]_h represent monomers reacted via catalytic reactions, monomers reacted via homogeneous reactions, polymer produced (and consumed) by catalytic reactions and polymer produced (and consumed) by homogeneous reactions, respectively.

Compared to homogeneous reactions, polymer formation happens at a much faster rate through catalytic reactions and does not need a relatively high temperature to occur. Furthermore, the heat generated by catalytic reactions increases the temperature of the system and helps carry on the homogeneous reactions.

Degree of polymerization is the only variable that is needed for simulating the viscosity of a urethane system.⁹ In this paper, viscosity is simulated by mixing rule, where the viscosity of the mixture is simulated based on the simulated mass fraction and viscosity of each component. Using group contribution method, Fu et al. simulated viscosity of each component separately.¹⁹ Viscosity of the polymer molecule was also simulated using average molecular weight of the polymer which was a function of the overall degree of polymerization. In this paper, molecular weight of the polymer is separated into homogeneous and catalytic molecular weights, each being simulated using the relevant degree of polymerization.

The following heuristics were used in this paper to facilitate the simulation of polyurethane polymerization.

The value of the reaction rate constant is independent of the catalyst being attached to alcohol or isocyanate moiety; it only varies based on the type of alcohol moieties (primary, secondary and hindered secondary) reacting with isocyanate moieties. For instance, k₁ and k₂ have the same values because they are both reaction rate coefficients for catalysed reaction between isocyanate and primary alcohol moieties.

Reaction rate coefficient for catalyst attachment is 100 times the reaction rate coefficient of secondary alcohol moieties reacting with isocyanate (propagation). Note that from a programming perspective, this translates to the more-basic assumption that catalyst attachment is very fast relative to propagation rates.

Heats of reaction are the same for isocyanate reacting with primary, secondary and hindered secondary alcohols, in both homogeneous and catalysed reactions.

The value of heat of reaction is zero for all catalyst attachment and catalyst detachment reactions, as heat is not generated during catalyst association and disassociation.

After reacting with an alcohol moiety, the catalyst attached to an isocyanate moiety is transferred to an alcohol moiety.

Experimental

Polyurethane gels were produced using RUBINATE M (Standard Polymeric MDI, PMDI) as isocyanate, Voranol 490 (Huntsman Company and Dow Chemical Co.) as alcohols/polyols, N,N-dimethylcyclohexylamine (DMCHA) as catalyst8 and Momentive L6900 as surfactant.

Each gel was prepared using Voranol 490, PMDI, 0.16% (mass) catalyst, and surfactant. Isocyanate index was kept at 1.1–1.2 for all gels. Chemicals were mixed in a plastic cup with a drill press at 2000 rpm. Mixing rate was kept constant for all gels as it may affect the viscosity profiles.²⁰ Then the cup was put into a polyurethane foam box to insulate the gel system and reduce the heat loss. Temperature profiles were obtained by a type-k thermocouple attached through a National Instruments SCB-68 box to a National Instruments PCI 6024E data acquisition card synchronized with LabVIEW software. Also a Cole-Parmer basic viscometer was used to measure viscosity profiles. All experiments were carried out at room temperature, in order to avoid deviations in reaction kinetics and molecular weights of the polymer²¹.

Results and discussions

Fig. 1 shows viscosity vs. temperature profiles for V490 gel reactions. It is shown that at the presence of a catalyst, viscosity increases much faster at lower temperatures. This indicates of different polymerization mechanisms for catalytic and homogeneous systems under the assumption that the temperature increase is closely related to the extent of reaction at these conversions.

Fig. 1 Viscosity vs. temperature profiles for homogeneous (squares) and catalytic (circles) V490 gel reactions.

This could be explained by a mechanism where molecules with catalyst-moiety complexes follow a chain growth polymerization mechanism while molecules without catalyst-moiety complexes follow a step growth polymerization.

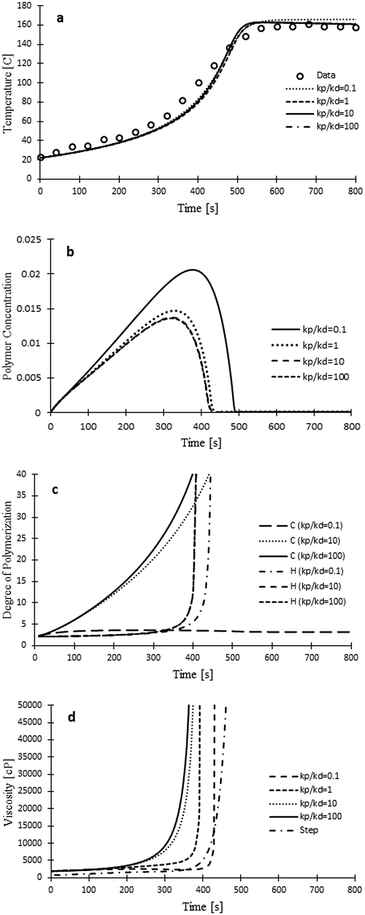
To simulate concentration and temperature profiles, Matlab's ODE45 function simultaneously solves 34 differential equations. Fig. 2 shows the simulation results superimposed with experimental data for the Voranol 490 gel reaction temperature profile. Eqn (8) was used to simulate the temperature profile based on reaction rates.

here, U is the overall heat transfer coefficient from the surroundings, A is the surface area which is the summation of base area and lateral area, ΔH_geli is the heat of gel reaction with respect to polyol i and ∑(n × C_p) is the summation of heat capacities of all the chemicals used.

Fig. 2 Simulation results and experimental data for Voanol 490 gel reaction temperature profile (a), simulation results for number of moles of catalyst versus time (b) and number of moles of isocyanate monomer (monomer A), polymer (P) and isocyanate (A) and alcohol (B) moieties (c).

Reaction rate kinetics for catalyst attachment and detachment reactions are presented in Table 3 where k_a, k_d, K, h_a, h_d and U are catalyst attachment reaction rate coefficient, catalyst disassociation rate coefficient, equilibrium constant, heat of reaction for catalyst attachment reactions, heat of reaction for catalyst disassociation reactions and heat transfer coefficient, respectively. Fig. 2 shows concentration profile for the catalyst based on the kinetics presented in Table 3.

Table 3 Reaction kinetics for catalyst attachment and detachment reactions

ka	kd	K	ha (J mol^−1)	hd (J mol^−1)	U (W m^−2 K^−1)
100 kp	0.001 kca	1000	0	0	1

---

Two methods are used to validate simulation results: (a) parametric trends that follow eqn (4) through (6) at low conversions and (b) the ability of the results to fit experimental data on temperature and viscosity trends. Fig. 3a–d provide these validations.

Fig. 3 Temperature (a), moles of polymer (b), catalytic and homogeneous degrees of polymerization (c) and viscosity (d) profile simulation results demonstrating the impact of k_p/k_d on profiles with k_a = 100 k_p.

Fig. 3a illustrates that fit of the simulation results to the temperature profile are relatively independent of the value of k_d, provided that k_p and k_a Arrhenius constant are maintained as constant. The interpretation of Fig. 3b–d is empowered by the assurance that all simulations follow the experimental data on temperature versus time.

Fig. 3b follows the trends of eqn (4), where decreasing frequency of disassociation (lower k_d) results in fewer new polymer chains forming and an overall lower concentration of polymers (concentration in mole per litre). A consequence of lower polymer concentrations at the same extents of reaction (same temperatures) is shown in Fig. 3c, where increases in degrees of polymerization (at low conversions) occur at lower values of k_d.

Finally, Fig. 3d illustrates the impact of k_p/k_d on simulation of viscosity. As k_p/k_d decreases, viscosity is shifted towards the viscosity simulated by the step growth model. Another important artefact of Fig. 3a–c is that when the value of k_d approaches and exceeds k_p, the chain-growth model asymptotically approaches step-growth performance.

Fig. 3c shows simulation results for catalytic and homogeneous degrees of polymerization for different ratios of k_p/k_d. It is shown that as k_d decreases, catalytic degree of polymerization increases, indicating the formation of more polymer molecules through catalysed reactions. However, an increase or decrease in k_d has a minor impact on homogeneous degree of polymerization, as homogeneous reactions are slightly affected by values of k_d. At high disassociation rate (small k_p/k_d), catalytic polymer concentration does not show a decrease in its profile although it is being consumed by the homogeneous reactions. Hence, the degree of polymerization does not rise as expected. This is due to the way the catalytic polymer is defined; it does not take into account the polymers with catalyst complexes that are consumed via homogeneous reactions. This results in polymer concentrations that are primarily affected by higher k_p/k_d.

Fig. 4 shows simulation results for a viscosity profile of Voranol 490 gel system using the old model (step growth) and the new model (chain growth). The new model seems to be simulating the viscosity more accurately, indicating that compared to the step growth mechanism, chain growth mechanism models the catalytic reactions in a more precise way. From t = 100 s to t = 350 s, there is no useful information on how A side and B side moieties react. As a result of insufficient information on the system, the model shows a gap between the experimental data and simulation results.

Fig. 4 Viscosity as a function of time (a) and temperature (b) of catalytic (circles) and homogeneous (squares) V490 gel systems, simulated by the old and new model. Solid lines represent the new catalytic chain growth model and the dashed lines represent old step growth model.

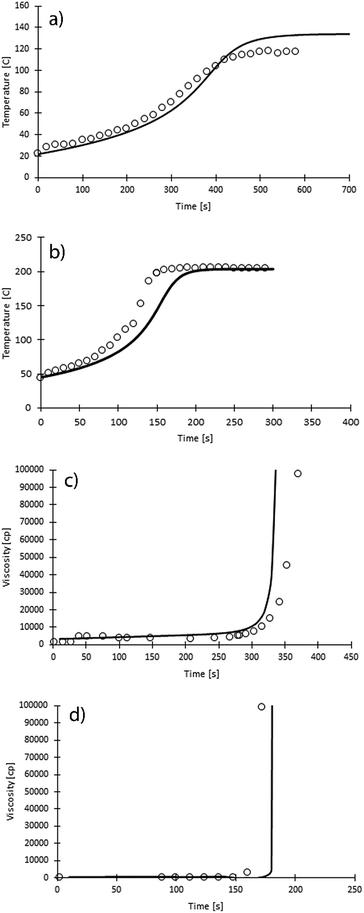
Two gel systems varying in isocyanate and polyol were chosen for testing the new approach on temperature and viscosity profiles. For the first system, Voranol 490 was substituted by Voranol 360 with no change in isocyanate, and for the second system, MDI was used instead of PMDI, with the polyol being Voranol 490. Isocyanate index and the amount of catalyst were identical to the Voranol 490 and PMDI system. Fig. 5 shows temperature and viscosity profiles for the new gel systems. The model lines are purely predictive to the kinetic parameters previously obtained. Simulation results show a reasonable fit to the experimental data, especially for V360 gel system. MDI is a solid substance and needs to be melted prior to mixing. This results in the solution having higher initial temperature, which impacts the kinetics of the reactions. The code has not been previously used for MDI gel systems, and was rarely used in higher initial temperatures. Besides, no modifications were made to improve its performance under the new conditions. However, the simulation results are relatively acceptable. The simulation results of both Voranol 360 and MDI systems validate the new approach and kinetic parameters.

Fig. 5 Temperature profiles for Voranol 360 and PMDI (a) and Voranol 490 and MDI (b) and viscosity profiles for Voranol 360 and PMDI (c) and Voranol 490 and MDI (d). The symbols and the solid lines represent experimental data and simulation results, respectively.

Conclusions

Since viscosity versus temperature profiles change with the addition of catalyst to a formulation, the polymer growth mechanism must also change with addition of catalyst. Matlab based simulations of the urethane-forming reactions were performed using step-growth homogeneous polymerization with chain-growth catalyst polymerization.

In general, simulation results for temperature profiles showed a good fit to the data, indicating reasonable heuristics for reaction rate coefficients, new catalytic reactions and relevant kinetic parameters. Degrees of polymerization resulting from chain-growth catalytic mechanisms were simulated and provide a more-rapid rise in overall degree of polymerization versus extent of reaction as compared to homogeneous step-growth mechanisms. This confirmed that catalysts result in larger k_p/k_d ratios as consistent with chain growth.

Viscosity profiles simulated by chain growth mechanism and homogeneous and catalytic degrees of polymerization show a better fit to experimental data, compared to the profiles simulated by the step growth model and one overall degree of polymerization. Based on the simulation results, it is possible to consider that polyurethane polymerization follows both chain growth and step growth mechanisms simultaneously; catalysed reactions follow a chain growth mechanism while the uncatalysed reactions undergo a step growth mechanism.

Acknowledgements

The authors thank the United Soybean Board for financial support of the experimental studies used to validate the modelling work. The authors thank FSI. Company providing foam formulas and technology support. None of the authors has conflicts of interest with companies producing RUBINATE M isocyanate, PolyCat8, Voranol 490 and Momentive L6900.

References

1. R. Chen, C. Zhang and M. R. Kessler, Anionic waterborne polyurethane dispersion from a bio-based ionic segment, RSC Adv., 2014, 4, 3547–3583.
2. C. Zhang and M. R. Kessler, Bio-based Polyurethane Foam Made from Compatible Blends of Vegetable-Oil-based Polyol and Petroleum-based Polyol, ACS Sustainable Chem. Eng., 2015, 3, 743–749.
3. E. Delebecq, J. Pascault, B. Boutevin and F. Ganachaud, On the Versatility of Urethane/Urea Bonds: Reversibility, Blocked Isocyanate, and Non-isocyanate Polyurethane, Chem. Rev., 2013, 113, 80–118.
4. V. W. A. P. Verhoeven, A. D. Padsalgikar, K. J. Ganzeveld and L. P. B. M Janssen, A Kinetic Investigation of Polyurethane Polymerization for Reactive Extrusion Purposes, Appl. Polym. Sci., 2006, 101, 370–382.
5. C. Zhang, R. Ding and M. R. Kessler, Reduction of Epoxidized Vegetable Oils: A Novel Method to Prepare Bio-Based Polyols for Polyurethanes, Macromo. Rapid Commun., 35, 1068–1074.
6. J. W. Blake, W. P. Yang, R. D. Anderson and C. W. Macosko, Adiabatic reactive viscometry for polyurethane reaction injection molding, Poly. Eng. Sci., 1987, 27, 1236–1242.
7. Y. T. Chen and C. W. Macosko, Kinetics and rheology characterization during curing of dicyanates, Appl. Polym. Sci., 1996, 62, 567–576.
8. E. B. M. Richte and C. W. Macosko, Kinetics of fast (RIM) urethane polymerization, Poly. Eng. Sci., 1978, 18, 1012–1018.
9. P. M. Cassagnau, F. Melis and A. Michel, Correlation of Linear Viscoelastic Behavior and Molecular Weight Evolution in The Bulk Urethane Polymerization, Appl. Polym. Sci., 1997, 65, 2395–2406.
10. T. Nagy, B. Antal, K. Czifrák, I. Papp, J. Karger-Kocsis, M. Zsuga and S. Kéki, New Insight into the Kinetics of Diisocyanate-Alcohol Reactions by High-Performance Liquid Chromatography and Mass Spectrometry, Appl. Polym. Sci., 2015, 123.
11. X. Sun, T. James and L. L. James, Chemorheology of poly(urethane/isocyanurate) formation, Polym. Eng. Sci., 1997, 37, 14–152.
12. A. Bouilloux, C. W. Macosko and T. Kotnour, Urethane polymerization in a counterrotating twin-screw extruder, Ind. Eng. Chem. Prod. Res. Dev., 1991, 30, 2431–2436.
13. G. Lu, D. Kalyon, I. Yilgör and E. Yilgör, Rheology and extrusion of medical-grade thermoplastic polyurethane, Poly. Eng. Sci., 2003, 43, 1863–1877.
14. E. C. Steinle, F. E. Critchfield, J. M. Castro and C. W. Macosko, Kinetics and conversion monitoring in a RIM themoplastic polyurethane system, Appl. Polym. Sci., 1980, 25, 2317–2329.
15. Y. Zhao, M. J. Gordon, A. Tekeei, F. H. Hsieh and G. J. Suppes, Modeling Reaction Kinetics of Rigid Polyurethane Foaming Process, Appl. Polym. Sci., 2013, 130, 1131–1138.
16. B. Radhakrishnan, E. Cloutet and H. Cramail, Synthesis of Uniform Polyurethane Particles by Step-Growth Polymerization in a Dispersed Medium, Colloid Polym. Sci., 2002, 280, 1122–1130.
17. R. Ghoreishi, Y. Zhao and G. J. Suppes, Reaction Modeling of Urethane Polyols Using Fraction Primay, Secondary and Hindered-Secondary Hydroxyl Content, J. Appl. Polym. Sci., 2014 DOI:10.1002/app.40388.
18. P. C. Hiemenz and T. P. Lodge, Polymer Chemistry, CRC Press, Boca Raton, FL, 2nd edn, 2007.
19. Z. Fu and G. J. Suppes, Group Contribution Modeling of Viscosity during Urethane Reaction, J. Polym. Eng., 2014, 35, 11–20.
20. P. Kolodziej, C. W. Macosko and W. E. Ranz, The influence of impingement mixing on striation thickness distribution and properties in fast polyurethane polymerization, Poly. Eng. Sci., 1982, 22, 388–392.
21. T. Ando, Effect of Reaction Temperature on Polyurethane Formation in Bulk, Polym. J., 1993, 25, 1207–1209.

---