Novel architecture for anomalous strengthening of a particulate filled polymer matrix composite†
Siva Kumar Reddya,
Devi Lalb,
Abha Misraa and
Praveen Kumar*b
aDepartment of Instrumentation and Applied Physics, Indian Institute of Science, Bangalore, India
bDepartment of Materials Engineering, Indian Institute of Science, Bangalore, India. E-mail: praveenk@materials.iisc.ernet.in
First published on 10th July 2015
Abstract
We propose an architecture for dramatically enhancing the stress bearing and energy absorption capacities of a polymer based composite. Different weight fractions of iron oxide nano-particles (NPs) are mixed in a poly(dimethylesiloxane) (PDMS) matrix either uniformly or into several vertically aligned cylindrical pillars. These composites are compressed up to a strain of 60% at a strain rate of 0.01 s−1 following which they are fully unloaded at the same rate. Load bearing and energy absorption capacities of the composite with uniform distribution of NPs increase by ∼50% upon addition of 5 wt% of NPs; however, these properties monotonically decrease with further addition of NPs so much so that the load bearing capacity of the composite becomes 1/6th of PDMS upon addition of 20 wt% of NPs. On the contrary, stress at a strain of 60% and energy absorption capacity of the composites with pillar configuration monotonically increase with the weight fraction of NPs in the pillars wherein the load bearing capacity becomes 1.5 times of PDMS when the pillars consisted of 20 wt% of NPs. In situ mechanical testing of composites with pillars reveals outward bending of the pillars wherein the pillars and the PDMS in between two pillars, located along a radius, are significantly compressed. Reasoning based on effects of compressive hydrostatic stress and shape of fillers is developed to explain the observed anomalous strengthening of the composite with pillar architecture.
1. Introduction
Particulate filled polymer matrix composites are widely used materials as they possess excellent combinations of mechanical, electrical, thermal and optical properties along with high flexibility and low density. In particular, dispersing metals and other conducting materials, such as graphene, carbon nanotubes, etc., especially above the percolation limit, dramatically improves the mechanical, electrical, thermal and electromagnetic shielding properties of polymer based composites.1–5 It should be noted that the percolation limit, identified as the concentration of the filler at which value or the slope of a materials property suddenly changes, for electrical conduction and a mechanical property, such as stiffness, can be widely different. Since the minimum volume fraction required for establishing a percolation network reduces with the particle size,6 the study of effects of nano-sized fillers in polymers has recently attracted significant attention.7–9 In addition to the reduction in the percolation limit, these nanometer sized fillers, because of their extremely small sizes, may also interact with the polymeric chains; this provides an extra control for manipulating various physical properties, such as strength, toughness, conductivity, etc.10–13Unlike electrical and thermal conductivities, which often show a monotonically increasing variation with the concentration of the conducting fillers,12,13 the mechanical strength of the polymer often do not vary monotonically with the filler concentration: for example, the strength may decrease with the concentration of fillers from the beginning itself or it may first increase and then decrease at higher concentrations.10,14 Since the mechanical strength of a composite is an important reliability parameter, it is important to not only study the effect of concentration of fillers on the mechanical behavior of the polymer based composites, but also discover techniques, based on microstructural engineering or novel architectures, for dramatically improving the mechanical properties of these composites.
Fabrication of architectured composites, where different micro-constituents are arranged in a well-defined fashion, is often used to enhance a target property, such as strength,15 energy absorption capacity,15 thermal conductivity,16,17 etc. The target properties of such architecture based composites can be superior to the predications of the rule of mixtures. Such an anomalous behavior arises as the architecture induces occurrence of favorable physical phenomena, such as crack deflection and crack arrest at particles (and hence improving fracture toughness),18 additional deformation of the matrix due to coordinated sliding of hard phase (and hence improving the stress bearing and energy absorption capacities),15 etc. Therefore, it is imperative to search for an architecture based solution for improving the mechanical behavior of a polymer based composite consisting of nanometer sized fillers or particulates; this is one of the goals of this study.
Unlike the conventional practices of uniformly distributing the fillers in the composites, the microstructure of architecture based composites is heterogeneous where the concentration of particulates widely varies across the sample.19 Generally, fabricating composites with heterogeneous microstructure or architectured structure with high degree of repeatability is extremely challenging. This work addresses this issue also by proposing a novel two-step processing technique for fabricating architectured composite. Thus, this work focuses on fabrication and evaluation of the mechanical behavior as function of filler concentration of a polymer based architectured composite. It is anticipated that fine-tuning of microstructure of these architectured composites may also give desired electrical, thermal and electromagnetic properties; however, these properties will be explored and reported later. Hence, it is speculated that the optimized composites can be used as joints (e.g., as thermal interface materials and package level interconnects in microelectronics, etc.), flexible conductors, etc., where moderate strength and high thermal and electrical conductivities are prerequisites. In addition, these composites can be used as lightweight dampers and shock absorbers also.
2. Experimental procedure
Poly(dimethylsiloxane) (PDMS) and iron(III) oxide nano-particles (NPs) were chosen as the polymer matrix and the filler, respectively. PDMS was chosen as it is one of most widely used polymers with well-defined mechanical behavior. Furthermore, PDMS is optically transparent, enabling direct observation of the movement of the colored fillers as the sample deforms.15 The details of the fabrication procedure of the two types of composites, with uniform and architectured microstructures, are outlined below.2.1 Composite with uniform microstructure
PDMS monomer and the appropriate linker (Dow Corning Sylgard® 184) were firstly mixed in volumetric ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 to produce the liquid polymer pre-form. Iron oxide NPs (supplied by Alfa Aesar), having mean size ∼40 nm, were then mixed into the pre-form. The concentration of NPs in the mixture was 5, 10, 15 or 20 wt%. The liquid mixture was then manually stirred to ensure uniform distribution of NPs in the polymer pre-form. The thoroughly mixed pre-form-NPs mixture was placed in a vacuum enclosure maintained at 10−2 Torr for 20 minutes for removing residual air bubbles. The air-bubble free mixture was then poured into a cylindrical Al mold of 13.2 mm diameter and 12 mm height followed by curing at 80 °C for 3 hours. As it will be shown later, such processing produced a composite with uniform distribution of the NPs in the PDMS; such a composite sample will henceforth be called as uniform composite. For comparison purposes, a few pure PDMS samples (i.e., without NP fillers) were also prepared following the same procedure.
1 to produce the liquid polymer pre-form. Iron oxide NPs (supplied by Alfa Aesar), having mean size ∼40 nm, were then mixed into the pre-form. The concentration of NPs in the mixture was 5, 10, 15 or 20 wt%. The liquid mixture was then manually stirred to ensure uniform distribution of NPs in the polymer pre-form. The thoroughly mixed pre-form-NPs mixture was placed in a vacuum enclosure maintained at 10−2 Torr for 20 minutes for removing residual air bubbles. The air-bubble free mixture was then poured into a cylindrical Al mold of 13.2 mm diameter and 12 mm height followed by curing at 80 °C for 3 hours. As it will be shown later, such processing produced a composite with uniform distribution of the NPs in the PDMS; such a composite sample will henceforth be called as uniform composite. For comparison purposes, a few pure PDMS samples (i.e., without NP fillers) were also prepared following the same procedure.
2.2 Architectured composite with heterogeneous microstructure
A two-step process comprising of following steps was used for fabricating architectured composite:Therefore, following the as-described two-step fabrication process, a composite with an architecture or heterogeneous microstructure was produced, wherein NPs were confined in disjoint cylindrical columns or pillars only. Such samples will henceforth be called as architectured composite. In these composites, the volume fraction of the pillars was ∼11%. Also, the 5, 10, 15 and 20% weight fractions of NPs in the pillars correspond to weight fractions of 2.9, 5.6, 8.3 and 10.8%, respectively, in the entire composite.
2.3 Mechanical testing of samples
Samples were tested in compression under ambient conditions. Samples were compressed to a nominal strain of 60% at a nominal strain rate of 0.01 s−1 and then fully unloaded using the same cross-head displacement rate. The mechanical tester (Instron-5967) was equipped with a 5 kN load cell, enabling accurate measurement of very small loads. For statistical purpose, at least 4 samples fabricated using the same conditions were tested. Video recording was conducted while performing a few of the mechanical tests for studying the deformation behavior of the samples. Representative samples were observed under scanning electron microscope (SEM) to study the distribution of NPs inside a composite.3. Experimental results
3.1 Microstructural observations
Fig. 2 shows a few representative micrographs revealing the distribution of NPs inside various composites. As shown in Fig. 2a, the distribution of NPs in the uniform composite was fairly uniform. Although the NPs were agglomerated at a few locations, they were generally disjoint. As shown in the inset of Fig. 2a, the shape of the NPs, large or small, remained spherical in the uniform composites. Interestingly, Fig. 2a also shows a few instances of “neck formation” in between spherical NPs. Such neck formation is signature of solid state sintering.20 Since the surface to volume ratio of NPs is very high, solid state sintering is possible even at low curing temperatures used in this study. However, as sintering often produces spherical particles, such a process will have no effect on the shape of the fillers in the uniform composites.Fig. 2b shows a tilted view of a pillar of an architectured composite. As shown in Fig. 2b, the interface between the pillar and a hole of the PDMS with holes sample was smooth. This confirms that the PDMS was fully cured after the first step of processing and no chemical interaction between the already cured PDMS and the newly poured mixture of PDMS pre-form and NPs occurred. Thus, the produced material can be qualified as a composite material with two distinct constituents: (i) the solid PDMS produced after the first step of the fabrication and (ii) the composite pillar which is basically a uniform composite comprising of NPs and PDMS. Interestingly, such two-step processing procedure is not only fairly easy to implement, but also capable of producing samples with highly repeatable microstructures.
Fig. 2c shows a high magnification image of a pillar revealing the shape and distribution of NPs in the pillars of an architectured composite. As shown in Fig. 2c, although, similar to the uniform composite, the distribution of NPs inside the pillars was uniform, the agglomerates of NPs in the pillars of architectured composites were relatively more elongated and generally aligned. Thus, even though the average size of the agglomerates and the disjoint particles in the pillars of the architectured composites were similar to those in the uniform composites, their shapes were drastically different; such differences may have significant effect on mechanical response of these composites.21
The differences in shape of particles and their agglomerates can be attributed to the side effects of the applied magnetic field when the mixture of PDMS pre-form and NPs was poured into the holes. In presence of the directional magnetic field, the iron-oxide particles not only align but also, upon magnetization, tend to attract the adjacent NPs forming elongated agglomerates (see Fig. 2c). Furthermore, as observed in Fig. 2a also, partial or incomplete sintering of powders in such elongated agglomerates or low coordination number arrangement will lead to formation of serrated, non-spherical, elongated particles, as shown in inset of Fig. 2a and indicated by broken arrows in Fig. 2c. These elongated and serrated particles can be thought as precursor of a large spherical particle that may eventually form. It should be noted that due to the large diffusion distances involved, complete sintering of particles in an elongated chain or low coordination number arrangement may require significantly longer periods as compared to the sintering of two isolated particles or large coordination number arrangements.20,22,23 Thus, if the diameter of steel rods used to prepare holes in PDMS was large enough to preclude the use of magnet for filling the PDMS pre-form–NPs mixture, the shape of NPs and their agglomerates in pillars would have been spherical. However, for the same number of pillars, this will lead to significant increase in the overall weight of NPs in the composite.
As shown in Fig. 2d, the distribution of NPs in pillars of an architectured composite was not uniform across the height of the pillar. Due to the downward magnetic force, more NPs were accumulated in the lower segment of the pillar as compared to the top region. However, the overall inhomogeneity reduced with an increase in the concentration of NPs in the pillars. Furthermore, as shown in Fig. 2c, the distribution of NPs was fairly homogeneous in the central segment of the pillar.
3.2 Stress–strain response
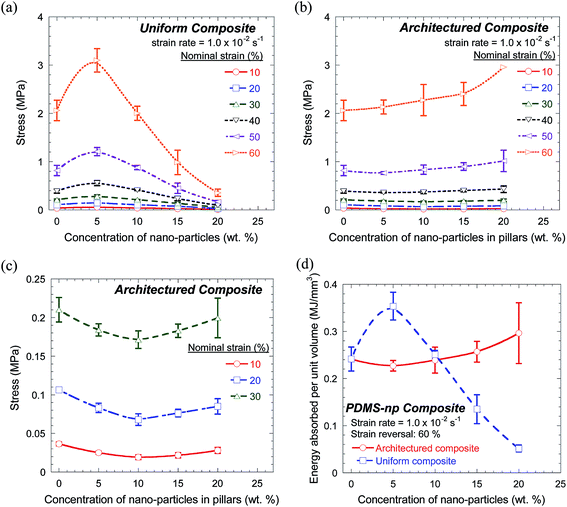
Fig. 3a and b show a few representative stress–strain plots obtained for uniform and architectured composites with different weight fractions of NPs, respectively. Fig. 3 readily reveals that all samples showed a “quasi-linear” (or slightly non-linear) stress–strain response at low strains (<25%) and a highly non-linear stress–strain behavior at higher strains. Furthermore, all samples showed a finite stress–strain hysteresis indicating loss of the strain energy during a cyclic loading; this may be attributed to loss of strain energy in the form of non-recoverable heat generated due to the rotation and sliding of long, coiled polymeric chains and the fictitious movement of NPs relative to the polymeric chains. Interestingly, Fig. 3 also reveals that the residual stress at the end of the cyclic loading was zero indicating negligible viscous effects under the quasistatic loading conditions.Fig. 4 summarizes Fig. 3 by showing stress imposed on a sample at particular strain (Fig. 4a–c) and the total energy absorbed by a composite during one complete loading–unloading cycle (Fig. 4d) as functions of the concentration of NPs. As shown in Fig. 4a, the stress bearing capacity of the uniform composite, irrespective of the strain, firstly increased upon addition of NPs up to a weight fraction of 5%, reaching a value almost ∼50% higher than that of pure PDMS, and subsequently, it monotonically decreased upon further addition of NPs. Eventually, upon addition of 20 wt% of NPs, the load bearing capacity of the uniform composite at strain 60% decreased to 1/6th of the pure PDMS.
The non-monotonous behavior in the load bearing capacity of the polymer–dispersion composites with concentration of fillers, similar to that shown in Fig. 4a, has also been reported by other groups also.14,24 This behavior can be attributed to the fact that the polymeric chains can strongly interact and bond with only limited amount of NPs (∼5 wt% in this case), beyond which the extra fillers segregate away from the polymeric chains. In a such case, these extra fillers act as stress concentrators leading to an overall decrease in the stress bearing capacity of the composite at high filler concentrations.14,24,25
As shown in Fig. 4b and c, the load bearing capacity of the architectured composite was a complex function of the strain as well as the concentration of NPs. As shown in Fig. 4c, at low strains (<30%), where the stress–strain behavior of the composite appears to be quasi-linear (Fig. 3b), the load bearing capacity of the architectured composite, firstly, decreased slightly with the addition of NPs in the pillars and then, increased. On the contrary, at higher strains (>30%) where the stress–strain behavior of composites were highly non-linear (Fig. 3b), the load bearing capacity of these composites monotonically increased with the concentration of NPs. As shown in Fig. 4b, the load bearing capacity of the architectured composites was maximized when the pillars comprised of 20 wt% of NPs and at a strain of 60%. Under such a condition, load bearing capacity of the architectured composite became ∼50% higher than that of pure PDMS. Possible reasons for such effects of strain and NPs concentration will be discussed later.
As shown in Fig. 4d, the energy absorbed by the composites during a loading–unloading cycle up to a compressive strain of 60% showed a similar trend as shown by the respective load bearing capacity of the composites at a strain of 60% (Fig. 4a and b). This is reasonable as the energy lost as heat (which, as explained earlier, is primarily responsible for formation of the stress–strain hysteresis loop) is proportional to the imposed strain energy, which, in turn, is proportional to the stress.
The variation of load bearing and energy absorption capacities of architectured composites with concentration of NPs are in sharp contrast to the trends shown by uniform composite. Interestingly, the latter is one of the constituents of the architectured composite. According to the rule of mixture for the iso-strain configuration, the load bearing capacity (and hence energy absorption capacity) of these architectured composites should show a trend similar to that of the uniform composite with stress values closer to that of pure PDMS (as volume fraction of pillars was only 11%). Possible reasons for the above anomalous behavior will be discussed later.
3.3 In situ observation of deformation behavior
Fig. 5 shows a few time-lapse images showing the important stages of the cyclic deformation of various tested samples (refer to ESI 1–3† for videos showing one full loading–unloading cycle). As shown in Fig. 5a, the uniform composites bulged out with compressive strain; however, it completely recovered its original shape, at least macroscopically, upon completion of the loading–unloading cycle. This suggests that these samples can be repetitively loaded–unloaded and hence can be useful for damping applications. In addition, Fig. 5a also reveals that the deformation along the vertical and the horizontal directions are smooth, resulting in uniform curvature. This suggests that the uniform composite behaved as a single phase material, confirming the efficacy of mixing of NPs in PDMS matrix.As shown in Fig. 5b, the PDMS with holes sample, similar to uniform composites, showed bulging wherein the holes as well as the material bent outwards. However, it is interesting to note that, especially at high compressive strains, the holes nearer to the center sideway flattened extensively whereas the holes further away from the center bent outwards with lesser sideway flattening (third and fourth pictures from left in Fig. 5b). Interestingly, the more flattening occurred in the central region of the holes. Such flattening of the circular holes indicates presence of large compressive stresses in the horizontal direction. It should be noted that the built-up of compressive stresses in the holes during compression test was also confirmed by occurrence of puncturing of a few holes from which the liquid dye oozed out (not shown here). Flattening of the holes and difference in their bending as well as flattening along the radial direction indicate that the deformation and deformation gradient in the PDMS with holes samples were not as gradual as they were in the case of the uniform composites. Furthermore, Fig. 5b also reveals that, as expected, the distance between two adjacent holes situated at same radial distance did not change with the deformation of the sample. A comparison of the left most and the right most images in Fig. 5b reveals that, similar to uniform composite (Fig. 5a), the sample recovered fully, at least macroscopically, at the end of unloading segment.
As shown in Fig. 5c, similar to uniform composites and PDMS with holes samples, the architectured composites also bulged upon compression and it also macroscopically fully recovered its original shape upon completion of the loading–unloading cycle. Furthermore, as shown in the third and the fourth images from the left in Fig. 5c, similar to PDMS with holes sample, the pillars were sideways flattened as the sample was compressed. Hence, additional compressive stress in radial direction, i.e., perpendicular to the direction of the externally applied compression, is also applied onto the pillars. In addition, as shown in Fig. 5c, the pillars in the central region of the sample did not bulge, but fattened. This indicates built-up of large compressive stresses in the pillars and the PDMS in their vicinity. Fig. 5c also reveals that, similar to the PDMS with holes samples and unlike uniform composites, the deformation and deformation gradient fields in the architectured composites were not gradual, resulting in highly inhomogeneous deformation of the composite. These observations will be later used to explain the anomalous strengthening behavior of the architectured composites.
4. Discussions
4.1 Anomalous strengthening of architectured composites
As shown in Fig. 5c and inferred from the geometrical analysis as well as Fig. 5b, although the pillars at a fixed radial distance moved away from each other in the tangential direction during compression, the distance between the two pillars lying along a radius approximately remained the same throughout the deformation. This adds to the complexity of the stress state. However, an implication of the generated stress state can be provided at least in a qualitative manner as follows: During the compression of a uniform composite as well as pure PDMS, the lateral expansion increases the radial as well as the tangential distance between any two points lying in a horizontal plane; however, the same is not true for the radial distance between points lying between two pillars bending in same direction in an architectured composite. Hence, the polymer in between two pillars lying on a radius will come under radial compression. This is consistent with the sideways flattening of the pillars (Fig. 5b and c), which, as mentioned previously, requires application of additional compressive stress in the horizontal direction. Furthermore, as mentioned earlier, similar compressive stress will also be generated in the non-bending fattening pillars and the adjacent PDMS located in the central region of the sample. Existence of this radial or horizontal compressive stress along with the vertical compressive stress leads to an increase in the total compressive hydrostatic stress in the sample. In practice, such an increase in the compressive hydrostatic stress increases the stress bearing capacity of the architectured composites.26 This additional deformation mode is absent in the uniform composites where NPs, being very small in size and not attached to the loading platens, do not act as effective anchoring points.In addition to the effect of the additional compressive stress in the pillars and the adjacent polymer in architectured composites, the drastic difference in the shapes of the NPs and their agglomerates in the uniform composite and the pillars of architectured composites may also aid to the observed anomalous strengthening of the latter. Since the surface area to volume ratio of a spherical inclusion is relatively smaller than that of an elongated inclusion, the elongated fillers can interact with the polymeric chains over larger length, resulting in relatively higher stress-bearing capacity of the polymer based composites.21 Hence, the inherent strength of the pillars of an architectured composite can actually be significantly higher than that of the uniform composite with the same concentration of NPs.
Fig. 6 compares the experimentally observed mechanical response of architectured composites with that of the predictions of rule of mixture for the iso-strain configuration; the latter is given as follows:
| σ = σ1v1 + σ2v2 | (1) |
 | ||
| Fig. 6 Comparison of experimental data with the prediction using eqn (1) at (a) small and (b) large strains. The open symbols represent the experimental data and the dotted lines show the predictions using eqn (1). The dashed arrow in (b) shows the trend where the best match between the experiment and eqn (1) was observed. | ||
As shown in Fig. 6a, the match between the predictions of eqn (1) and the experimental data at low strains was the best for the architectured composites having the highest concentration of the NPs. On the other hand as shown in Fig. 6b, at high strains, the best match between predictions using eqn (1) and the experimental data gradually shifted towards the composites comprising of pillars with lower concentration of NPs (as indicated by dashed arrow). As explained in the context of Fig. 5, the overall compressive hydrostatic stress in the pillars increased with the strain and hence the architectured composites with any weight fraction of NPs will anomalously strengthen with the compressive strain. Hence, with strain the experimental data points shifted upwards relative to the iso-strain model. It should be noted that iso-strain model does not account for the effects of the lateral compressive stresses and the hydrostatic stress on the mechanical response of a material. This explains the effect of strain on the stress bearing capacity of the architectured composites samples as shown in Fig. 6.
However, the variation of stress with the NP concentration, as shown in Fig. 6, is a bit perplexing. It is speculated that the effect of the non-homogeneity in distribution of NPs in the pillars due to the sedimentation of NPs under the applied magnetic field, which results in higher concentration of NPs near the bottom of the sample (Fig. 4d), is more significant in the architectured composites with lesser concentration of NPs. Hence, in the architectured composites with lesser concentration of NPs, a significant volume fraction of the pillar becomes deprived of the fillers, resulting in loss of its strength. Furthermore, the bottom segment of the pillars, where NP concentration becomes very high, will also be weaker because of increase in the local concentration of NPs and formation of large sized agglomerates; both of these result in an increase in stress concentration and hence a decrease in the stress bearing capacity of the particulate filled polymer based composites.27,28 In addition, the chemical inertness between the pillar and the PDMS with holes constituents of architectured composites reduces the effectiveness in the load transfer from one component of the composite to another, making the architectured composites with low NP concentration weaker than the pure PDMS.
4.2 Constitutive relationship
Fig. 7a shows a few representative loading curves up to ∼30% of strain, ε, of various types of samples, including pure PDMS, PDMS with holes, a uniform composite and an architectured composite. Fig. 7a also shows the best fit curves determined using the following form of Mooney–Rivlin equation:29
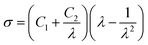 | (2) |
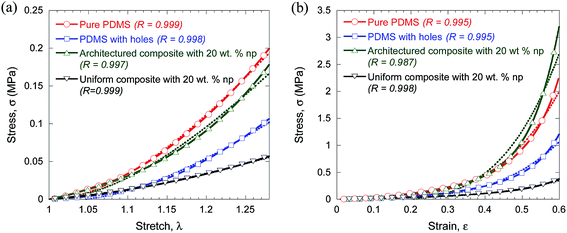 | ||
| Fig. 7 Curve fitting of loading segments using (a) eqn (2) up to a strain of 28% and (b) eqn (3) up to a strain of 60%. The fitted curves are shown by dotted lines whereas the experimental data are shown by solid lines with a few open symbols. The curve fitting parameter, R, is listed in the legend. | ||
Since Mooney–Rivlin model is suitable only at small strains, eqn (2) cannot aptly represent the entire stress–strain data (i.e., up to strain of 60%) imposed on the samples tested in this study. Therefore, as proposed in a previous work,15 the following polynomial relationship was used to capture the entire stress–strain data:
| σ = ε(a + bε3) | (3) |
An important feature of eqn (3) is that it is a polynomial consisting of only two terms, making it computationally inexpensive for both curve-fitting exercise and performing predictions. The versatility of eqn (3) can be attributed to the superposition of a linear term and a high power term: at lower strains, the linear term dominates giving a linear stress–strain behavior whereas at very high strains, the high power term dominates capturing the highly non-linear behavior. In addition, at moderate strains, both terms contribute significantly producing a slightly non-linear or quasi-linear stress–strain response. Since the stress–strain behavior of elastomers transitions from linear to slightly non-linear to highly non-linear shape with strain, eqn (3) can capture the entire stress–strain plot, as shown in Fig. 7.
5. Conclusions
(1) Composites of PDMS and iron(III) oxide NPs were prepared following two schemes. In the first scheme, NPs were distributed uniformly in PDMS (uniform composite) whereas in the second scheme, a square array of pillars, each comprising of uniform mixture of NPs and PDMS, were inserted into PDMS in iso-strain configuration (architectured composite).(2) For fabricating architectured composites, a two-step processing route was adopted, where firstly, the solid PDMS skeleton with several through holes was prepared and subsequently, these holes were filled by the liquid mixture of NPs and PDMS pre-form with aid of a downward magnetic field. The overall distribution of NPs in the pillars can be considered as uniform. Also, the particles in the pillars of architectured composites were more elongated whereas they were spherical in uniform composites.
(3) The load bearing capacity of uniform composites increased upon addition of NPs, reaching a maximum of 1.5 times the pure PDMS upon addition of 5 wt% of NPs, and then gradually decreased to 1/6th of the pure PDMS upon addition of 20 wt% of NPs. On the other hand, the load bearing capacity of architectured composites at high strains (≥40%) monotonically increased with addition of NPs in the pillars. Similar behavior was also shown by the total energy absorbed during one loading–unloading cycle.
(4) All composites tested in this study bulged upon compression and macroscopically recovered their original shape upon unloading. However, the deformation field in the architectured composites was highly inhomogeneous. Under compressive loads, the pillars further away from the central region bent outwards and sideways flattened. On the other hand, the pillars in the central region fattened and did not bulge significantly.
(5) Combined effects of high compressive hydrostatic stress and elongated shaped fillers in the pillars of the architectured composites may explain their anomalous strengthening.
Acknowledgements
The work was partially supported by an IISc-STC grant to PK (ISTC0316).References
- J. C. Grunlan, A. R. Mehrabi, M. Bannon and J. L. Bahr, Adv. Mater., 2004, 16, 150 CrossRef CAS PubMed.
- N. Li, Y. Huang, F. Du, X. B. He, X. Lin, H. J. Gao, Y. Ma, F. Li, Y. Chen and P. C. Eklund, Nano Lett., 2006, 6, 1141 CrossRef CAS PubMed.
- H. Pang, T. Chen, G. Zhang, B. Zeng and Z. Li, Mater. Lett., 2010, 64, 2226 CrossRef CAS PubMed.
- W. L. Song, P. Wang, L. Cao, A. Anderson, M. J. Meziani, A. J. Farr and Y. P. Sun, Angew. Chem., Int. Ed., 2012, 51, 6498 CrossRef CAS PubMed.
- W. Songa, M. Cao, M. Lu, S. Bi, C. Wang, J. Liu, J. Yuan and L. Fan, Carbon, 2014, 66, 67 CrossRef PubMed.
- G. P. Moriarty, J. H. Whittemore, K. A. Sun, J. W. Rawlins and J. C. Grunlan, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 1547 CrossRef CAS PubMed.
- J. Cho, M. S. Joshi and C. T. Sun, Compos. Sci. Technol., 2006, 66, 1941 CrossRef CAS PubMed.
- V. Ganesan and A. Jayaraman, Soft Matter, 2014, 10, 13 RSC.
- I. G. Garcíaa, M. Paggib and V. Mantiča, Eng. Fract. Mech., 2014, 115, 96 CrossRef PubMed.
- R. Kitey and H. V. Tippur, Acta Mater., 2005, 53, 1153 CrossRef CAS PubMed.
- S. Fu, X. Feng, B. Lauke and Y. Mai, Composites, Part B, 2008, 39, 933 CrossRef PubMed.
- A. M. Marconnet, N. Yamamoto, M. A. Panzer, B. L. Wardle and K. E. Goodson, ACS Nano, 2011, 5, 4818 CrossRef CAS PubMed.
- A. Patole and G. Lubineau, Carbon, 2015, 81, 720 CrossRef CAS PubMed.
- D. M. Bigg, Polym. Compos., 1987, 8, 115 CrossRef CAS PubMed.
- A. Misra and P. Kumar, Sci. Rep., 2014, 3, 2056 Search PubMed.
- C. Cao, A. Yu and Q. Qin, International Journal of Architecture, Engineering and Construction, 2012, 1, 14 CrossRef.
- P. Kumar and S. Awasthi, J. Compos. Mater., 2014, 48, 1391 CrossRef CAS PubMed.
- E. Munch, M. E. Launey, D. H. Alsem, E. Saiz, A. P. Tomsia and R. O. Ritchie, Science, 2008, 322, 1516 CrossRef CAS PubMed.
- L. J. Huang, L. Geng and H.-X. Peng, Prog. Mater. Sci., 2015, 71, 93 CrossRef CAS PubMed.
- R. M. German, Sintering Theory and Practices, Wiley-Interscience, John Wiley & Sons, Inc, New York, US, 1996 Search PubMed.
- L. E. Nielsen, J. Compos. Mater., 1967, 1, 100 CAS.
- W. H. Rhodes, J. Am. Ceram. Soc., 1981, 64, 19 CrossRef CAS PubMed.
- F. F. Lange, J. Am. Ceram. Soc., 1984, 67, 83 CrossRef CAS PubMed.
- Y. Zhang, Y. Zhu, G. Lin, R. S. Ruoff, N. Hu, D. W. Schaefer and J. E. Mark, Polymer, 2013, 54, 3605 CrossRef CAS PubMed.
- L. E. Nielsen, J. Appl. Polym. Sci., 1966, 10, 97 CrossRef CAS PubMed.
- W. A. Spitzig and O. Richmond, Polym. Eng. Sci., 1979, 19, 1129 CAS.
- H. H. Kausch and G. H. Michler, J. Appl. Polym. Sci., 2007, 105, 2577 CrossRef CAS PubMed.
- A. Dorigato, Y. Dzenis and A. Pegoretti, Mech. Mater., 2013, 61, 79 CrossRef PubMed.
- A. Rudin, The Elements of Polymer Science and Engineering, Academic Press, Elsevier, San Diego, US, 1999 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra10714h |
| This journal is © The Royal Society of Chemistry 2015 |