Distortion–interaction analysis along the reaction pathway to reveal the reactivity of the Alder-ene reaction of enes

Abstract

The reactivity of hetero-substituted propylene in uncatalyzed Alder-ene type reactions was investigated using CBS-QB3, G3B3, M11, and B3LYP methods, and the results are interpreted by distortion–interaction analysis of both the transition states and the complete reaction pathways. The reactivity trend for third-period element substituted ene reactants (ethylidenesilane, ethylidenephosphine, and ethanethial) is higher than that of the corresponding second-period element substituted ene reactants (propylene, ethanimine, and acetaldehyde). Theoretical calculations also indicate that for the same period element substituted ene reactants, the reactivity trend is ethylidenesilane > ethylidenephosphine > ethanethial, and propylene > ethanimine > acetaldehyde. Application of distortion–interaction analysis only of the transition states does not give a satisfactory explanation for these reactivities. Using distortion–interaction analysis along the reaction pathways, we found that the reactivity is mainly controlled by the interaction energy. A lower interaction energy along the reaction pathway leads to an earlier transition state and a lower activation energy, which also can be attributed to orbital interaction, closed-shell repulsion, and static repulsion. In some cases, the distortion energy also influences the reactivity.

---

Introduction

There are various factors that influence the reactivity of bimolecular reactions, including reactant flexibility, orbital interaction, close-shelled repulsion, and strain repulsion.¹ However, these effects are usually mixed in one reaction, and are difficult to isolate. Therefore, some theoretical methods and models, such as frontier molecular orbital theory,² the Hammond postulate,³ Marcus theory,⁴ and the distortion–interaction model,⁵ have been proposed and used to qualitatively and quantitatively explain these reactivity differences.

During the past three decades, the distortion–interaction model, which was proposed by Morokuma,⁶ Houk,⁷ and Bickelhaupt,⁸ has been widely used to explain the energy difference of the transition states of bimolecular reactions.⁹ As shown in Fig. 1, the distortion–interaction model treats the activation barrier of a transition state as two quantities, distortion energy (ΔE^≠_dist) and interaction energy (ΔE^≠_int), and is directly used for transition states in bimolecular reactions. ΔE^≠_dist is the energy required to distort two fragments into the transition state geometries without allowing interaction between them, and ΔE^≠_int is the energy change upon interaction of the two distorted fragments.¹⁰

Fig. 1 Relationship between activation (ΔE^≠), distortion (ΔE^≠_dist), and interaction energies (ΔE^≠_int).

The activation energy is then defined as ΔE^≠ = ΔE^≠_dist + ΔE^≠_int. In 2007, Houk's group reported a distortion–interaction model to explain the reactivity trends of 1,3-dipolar cycloadditions.¹¹ The activation energies of 1,3-dipolar cycloadditions are well correlated with the distortion energies, in which most of the distortion energy involves the bending of 1,3-dipoles. When we attempted to use this model to study the reactivity of ozone and sulfur dioxide in 1,3-dipolar cycloaddition¹² and Diels–Alder cycloaddition between cumulenes and dienes,¹³ it did give a satisfactory explanation. However, distortion–interaction analysis along the reaction pathways clearly determines the factors that control the reactivity.^12,13 In the present work, distortion–interaction analysis of both transition states and the complete reaction pathways is used to study the reactivity of some hetero-Alder-ene reactions.

The Alder-ene reaction, which was first reported by Alder in 1943,¹⁴ occurs between an alkene and an allylic hydrogen (ene), forming a new σ-bond with migration of the ene double bond and a 1,5-hydrogen shift. Alder-ene reactions have been extensively reviewed¹⁵ because of their wide application in the synthesis of complex molecules and nature products.¹⁶ Including heteroatoms in Alder-ene reactions, which are called hetero-Alder-ene reactions, expands the scope of this type of reaction¹⁷ (Fig. 2).

Fig. 2 Alder-ene and hetero-Alder-ene reactions.

Hetero-Alder-ene reactions with a series of enophile parts have attracted considerable attention, both experimentally and theoretically.¹⁸ However, investigation of the reactions of mutation of ene parts has been rarely reported, even though it is significant for the design of new types of reactions.¹⁹ To the best of our knowledge, the reactivity of heteroatom substituted ene parts in hetero-Alder-ene reactions is still unclear.

Usually, an uncatalyzed Alder-ene or hetero-Alder-ene reaction occurs via a concerted six-membered aromatic transition state.²⁰ When Lewis acids are used, some stepwise mechanisms have also been reported.²¹ In the present work, the reactivities for the mutation of ene parts in hetero-Alder-ene reactions were theoretically investigated, and the difference in the reactivities are explained by distortion–interaction analysis of both transition states and the complete reaction pathways.

Computational methods

All of the calculations were carried out with the Gaussian 09 series of programs.²² The reaction barriers and reaction energies were calculated at the B3LYP/6-311++G(d,p), M11/6-311++G(d,p), G3B3, and CBS-QB3 levels of theory. B3LYP²³ is the most widely used hybrid generalized gradient approximation functional.²⁴ The M11 functional,²⁵ which was recently proposed by the Truhlar group, can give more accurate energetic information.²⁶ Complete basis set (CBS) methods²⁷ strive to eliminate errors that arise from basis set truncation in quantum mechanical calculations by extrapolating to the CBS limit by exploiting the N⁻¹ asymptotic convergence of second-order Møller–Plesset (MP2) pair energies calculated from pair natural orbital expansions. In particular, CBS-QB3 uses B3LYP/6-311G(2d,d,p) geometries and frequencies,²⁸ followed by CCSD(T), MP4(SDQ), and MP2 single-point calculations with a CBS extrapolation.²⁸ While CBS-QB3 is generally reliable, in some cases it has been shown to give anomalous activation energies.²⁹ Consequently, in this work, the geometries and energies were also calculated using the G3B3 method.³⁰ G3B3, which was developed from Gaussian-3 (G3) theory,³¹ is a high-level composite method that combines a series of well-defined ab initio calculations to reach a total energy effectively at the QCISD(T)/(T,full)/G3Large level. The G3Large basis set is an improved version of the large 6-311+G(3df,2p) basis set with additional polarization for the second row (3d2f) and reduction of the first row (2df), and provides a better balance of the polarization functions.³² These four methods, which have been benchmarked for 1,3-dipolar cycloadditions, give more accurate relative energies.³³

In this work, the intrinsic reaction coordinates³⁴ of all Alder-ene and hetero-Alder-ene type transition states were used to calculate the relative energies and geometries of the reaction coordinates. Every geometry of the reaction coordinates (listed in the ESI†) is separated into ene and enophile parts. The distortion energy (ΔE^≠_dist) is the energy difference between the energy of the distorted ene and enophile parts and the energy of the fully optimized ene and enophile parts. The interaction energy (ΔE^≠_int) is the energy difference between the energy of the geometry of the reaction coordinate and the energy of the relative distorted ene and enophile parts. When the distortion, interaction, and total energies are plotted, the forming C–H bond is used to represent the reaction coordinate. Therefore, the reactivity of various enes can be compared with the same reaction coordinate in one plot to avoid the influence of the different atomic radii of C, Si, N, P, O, and S atoms.

Results and discussion

Reactions (1)–(6) in Scheme 1 were studied in present work. The activation energies (relative energies of transition states 2-ts, 5-ts, 8-ts, 11-ts, 14-ts, and 17-ts) and reaction energies (relative energies of complexes 3, 6, 9, 12, 15, and 18) calculated by CBS-QB3, G3B3, M11, and B3LYP methods are listed in Table 1.

Scheme 1 Alder-ene or hetero-Alder-ene reactions of propylene, ethylidenesilane, ethanimine, ethylidenephosphine, acetaldehyde, and ethanethial with ethylene.

Table 1 Activation energies (ΔG^≠) and reaction energies (ΔG^≠_rxn) for Alder-ene and hetero-Alder-ene reactions of propylene, ethylidenesilane, ethanimine, ethylidenephosphine, acetaldehyde, and ethanethial with ethylene

Method	CBS-QB3	G3B3	M11	B3LYP
2-ts	45.1	46.6	43.5	47.0
3	−10.5	−10.2	−11.6	−5.5
5-ts	23.5	24.3	23.4	26.8
6	−37.6	−37.3	−39.9	−32.5
8-ts	49.2	50.5	47.5	49.9
9	−4.2	−3.8	−8.1	−0.8
11-ts	34.8	36.8	33.1	37.0
12	−13.4	−12.7	−15.2	−8.4
14-ts	52.1	52.9	51.2	52.2
15	5.1	5.4	4.0	9.9
17-ts	35.3	37.0	33.9	37.1
18	−9.7	−9.1	−10.7	−4.3

---

Propylene 1 reacts with ethylene to form product 3 via transition state 2-ts. The CBS-QB3 and G3B3 calculated activation free energies are 45.1 and 46.6 kcal mol⁻¹, respectively. M11 gives a similar value of 43.5 kcal mol⁻¹ for the activation free energy, while B3LYP overestimates the activation free energy by about 4 kcal mol⁻¹. CBS-QB3, G3B3, and M11 predict that this reaction is exothermic (−10.5, −10.2, and −11.6 kcal mol⁻¹, respectively), whereas the B3LYP result is about 5 kcal mol⁻¹ less exothermic (−5.5 kcal mol⁻¹). As shown in Scheme 2, in transition state 2-ts, the length of the C1=C2 double bond in the propylene moiety increases by 0.05 Å comparing with that of the propylene reactant. The length of the C2–C3 bond in the propylene moiety decreases by about 0.09 Å compared with the bond distance in 1, and the C1–C2–C3 angle of propylene decreases from 125.3° in 1 to 119.5° in 2-ts. The newly forming C1–C4 bond distance is 2.14 Å. The forming C5–H and breaking C3–H bond distances are 1.45 and 1.34 Å, respectively. In reaction (2), ethylidenesilane 4 reacts with ethylene to form product 6 via transition state 5-ts. Compared with reaction (1), the energy barrier of this reaction is much lower. In transition state 5-ts, the newly forming Si–C4 bond is 0.15 Å longer than that in transition state 2-ts, partially because of the larger radius of the Si atom. The C3–C2–Si angle is 116.1° in 5-ts, which is 3.4° less than the corresponding angle in 2-ts. These differences indicate that transition state 5-ts can be reached slightly earlier than 2-ts.

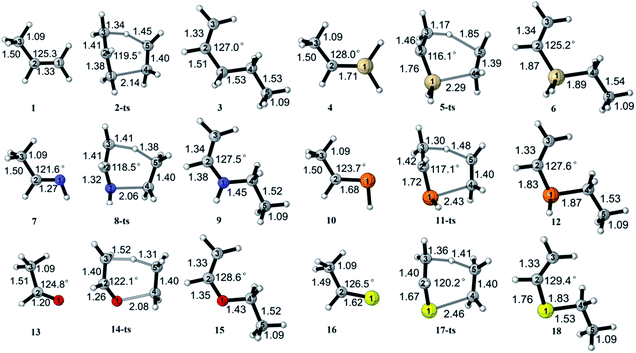Scheme 2 Geometry information of reactants, transition states, and products of hetero-Alder-ene reactions, by the CBS-QB3 method.

The hetero-Alder-ene reaction between ethanimine 7 and ethylene was also investigated. CBS-QB3, G3B3, and B3LYP methods gave similar activation free energies of 49.2, 50.5 and 49.9 kcal mol⁻¹, respectively, while M11 gave a slightly lower activation free energy of 47.5 kcal mol⁻¹. All of these calculated energy barriers are 2–4 kcal mol⁻¹ higher than those for reaction (1) calculated with the same methods. CBS-QB3, G3B3, M11, and B3LYP all predict that this reaction is exothermic (−4.2, −3.8, −8.1, and −0.8 kcal mol⁻¹, respectively). In the geometry of transition state 8-ts (see Scheme 2), the newly forming N–C4 bond distance is 2.06 Å, and the forming C5–H and breaking C3–H bond distances are 1.38 and 1.41 Å, respectively, which indicates that transition state 8-ts comes later than 2-ts in reaction (1). When a phosphorus atom replaces the nitrogen atom in reaction (4), the calculated activation free energy also decreases, and reaction (4) is more exothermic than reaction (3). As shown in Scheme 2, in the geometry of transition state 11-ts, the length of the newly forming P–C4 bond is 0.37 Å longer than the corresponding length in transition state 8-ts, which can partly be attributed to the larger radius of the phosphorus atom. Moreover, the length of the C2=P bond of the ethylidenephosphine moiety in transition state 11-ts is 0.04 Å longer than that in reactant 10, and the C3–C2–P angle decreases by 6.6°, which is 1.4° less than the corresponding angle in 8-ts. These differences in geometry demonstrate that transition state 11-ts can be reached slightly earlier than 8-ts.

In reaction (5) in Scheme 1, acetaldehyde 13 reacts with ethylene to form the product 15 via transition state 14-ts. The CBS-QB3, G3B3, M11 and B3LYP methods give similar activation free energies of 52.1, 52.9, 51.2, and 52.2 kcal mol⁻¹, respectively. The energy barrier of reaction (5) is higher than that of reactions (1) and (3), and the geometry information also indicates that transition state 14-ts comes later than the corresponding transition states for reactions (1) and (3). When ethanethial is used as a reactant in the hetero-Alder-ene reaction, the activation free energy is lower than that for acetaldehyde, which is similar to the comparison between reactions (3) and (4).

The computational results indicate that the reactivity trend for the terminal group in the ene reactant substituted hetero-Alder-ene reactions in Scheme 1 is O < NH < CH₂, and the reactivity of third-period element substituted ene reactants (4, 10, and 16) is higher than that of the corresponding second-period element substituted ene reactants (1, 7, and 13).

Distortion–interaction energy analysis of the transition states was first used to explain the reactivity trends of these Alder-ene reactions, and the results are shown in Table 2. The total activation energy (ΔE^≠) is devolved into the distortion energy (ΔE^≠_dist) and interaction energy (ΔE^≠_int) of the two distorted reactants. CBS-QB3 calculation of the Alder-ene reaction of propylene 1 to ethylene gives a distortion energy of 42.0 kcal mol⁻¹ and an interaction energy of −9.1 kcal mol⁻¹. For the reaction with ethylidenesilane 4, the distortion energy in transition state 5-ts is 19.6 kcal mol⁻¹ lower than that in 2-ts, and the interaction energy of those two reactions are similar. Distortion–interaction energy analysis of the transition states indicates that the reactivity difference of propylene 1 and ethylidenesilane 4 is controlled by distortion energy because of the greater flexibility of the C=Si double bond. For the hetero-Alder-ene reaction of ethanimine 7, the distortion energy is 43.4 kcal mol⁻¹, which is 10.3 kcal mol⁻¹ higher than that for ethylidenephosphine 10. Moreover, the interaction energy for transition state 8-ts is 3.8 kcal mol⁻¹ higher than 11-ts. Therefore, the reactivity of ethanimine 7 and ethylidenephosphine 10 are determined by both of the distortion energies, which mainly come from the ene parts, and interaction energies. Furthermore, the different reactivity of acetaldehyde 13 and ethanethial 16 can also be attributed to the greater flexibility of the C=S double bond. Therefore, the reactivity of third-period element substituted ene reactants (4, 10, and 16) is higher than that of the corresponding second-period element substituted ene reactants (1, 7, and 13) because of the greater flexibility of the C=X double bond (X = SiH₂, PH, or S) based on distortion–interaction analysis of the transition states.

Table 2 Distortion–interaction energy analysis of the transition states of the Alder-ene reactions calculated by the CBS-QB3 method. The values are in kcal mol⁻¹

	ΔEdist(ene)	ΔEdist(enophile)	ΔEdist	ΔEint	ΔE^≠
2-ts	30.3	11.7	42.0	−9.1	32.9
5-ts	13.7	8.7	22.4	−10.9	11.5
8-ts	31.8	11.5	43.4	−6.3	37.1
11-ts	22.5	10.5	33.1	−10.1	22.9
14-ts	42.9	10.1	52.9	−13.0	40.0
17-ts	25.8	9.2	35.1	−11.7	23.4

---

Compared with the Alder-ene reactions of propylene 1, ethanimine 7, and acetaldehyde 13, the lowest distortion energy and lower interaction energy of transition state 2-ts result in the lowest activation energy. The highest distortion energy of transition state 14-ts contributes to the highest activation energy. Distortion–interaction energy analysis of the transition states shows that the reactivity trend of the Alder-ene reactions for propylene 1, ethanimine 7, and acetaldehyde 13 is controlled by both the distortion energy and interaction energy.

Compared with distortion–interaction analysis of the transition state, distortion–interaction analysis along the complete reaction pathway is a more powerful tool to analyze the reactivity trends for similar bimolecular reactions.³⁵ In the present work, we used the high accuracy CBS-QB3 method to calculate the distortion and interaction energies along the complete reaction pathway to explain the reactivity trends for Alder-ene reactions with different ene reactants. The computational results are summarized in Fig. 3–7.

Fig. 3 Distortion, interaction, and total energies along the reaction pathways for ene-reactions (1) (black) and (2) (red) calculated at the CBS-QB3 level of theory. The solid lines are the reaction energies. The dashed lines are the distortion energies. The dotted lines are the interaction energies.

The distortion, interaction, and total energies along the reaction pathways for ene-reactions (1) (black lines) and (2) (red lines) are shown in Fig. 3. For both reaction (1) and (2), when the ene moiety and enophile moiety come close, the distortion energy increases. The distortion energy for reaction (2) is higher than that for reaction (1). In reaction (2), the interaction energy decreases when the two parts of the reactants come together. In reaction (1), however, this energy increases when the forming C–H bond length is longer than 1.85 Ǻ, and then it decreases. The repulsion between propylene 1 and ethylene is also clearly shown in the interaction energy along the complete reaction pathway, which can be attributed to the lower orbital repulsion between ethylidenesilane 4 and ethylene. The lower interaction energy of reaction (2) than reaction (1) leads to the earlier transition state. Therefore, the distortion energy of transition state 5-ts is lower than that of transition state 2-ts, which is also obtained by distortion–interaction analysis of the transition states. The distortion–interaction analysis along the complete reaction pathways indicates that the lower interaction energy for reaction (2) results in the lower activation energy, which is more accurate than distortion–interaction analysis of the transition states.

Reactions (3) (black lines) and (4) (red lines) are compared in Fig. 4. The distortion energies for reactions (3) and (4) are close along the complete reaction pathway. However, the interaction energy for reaction (4) along the complete reaction pathway is significantly lower than that for reaction (3). The lower interaction energy leads to a lower activation energy and an earlier transition state. Therefore, the distortion energy of transition state 8-ts is higher than that of 11-ts.

Fig. 4 Distortion, interaction, and total energies along the reaction pathways for ene-reactions (3) (black) and (4) (red) calculated at the CBS-QB3 level of theory. The solid lines are the reaction energies. The dashed lines are the distortion energies. The dotted lines are the interaction energies.

Reactions (5) (black lines) and (6) (red lines) are compared in Fig. 5. Along the complete reaction pathway, both the distortion and interaction energies for reaction (6) are lower than those for reaction (5). Therefore, the relative energy of transition state 17-ts is lower than that of 14-ts. The lower interaction energy can be attributed to the lower orbital repulsion between ethanethial 16 and ethylene, and the lower distortion energy comes from the greater flexibility of ethanethial 16.

Fig. 5 Distortion, interaction, and total energies along the reaction pathways for ene-reactions (5) (black) and (6) (red) calculated at the CBS-QB3 level of theory. The solid lines are the reaction energies. The dashed lines are the distortion energies. The dotted lines are the interaction energies.

In Fig. 6, the reactivities of propylene 1, ethanimine 7, and acetaldehyde 13 are compared by distortion–interaction analysis along the reaction pathways. The CBS-QB3 calculations indicate that along the complete reaction pathways, the distortion energies for reactions (3) and (5) are essentially the same, while the distortion energy for reaction (1) is a little higher because of the stronger C=C double bond in propylene 1. The tendencies of the interaction energies along the complete reaction pathways for these three reactions are approximately the same: increasing when the forming C–H bond is longer than 1.8 Å, and then decreasing. The relative interaction energies along the reaction pathways for reactions (3) and (5) are higher than reaction (1) because of the closed-shell repulsion by the nitrogen atom in ethanimine 7 or the oxygen atom in acetaldehyde 13.¹³ The lower interaction energy for reaction (1) leads to a lower activation energy and an earlier transition state. Compared with the interaction energy curves of reaction (3) and (5), the faster decreasing rate of ethanimine 7 leads to an earlier transition state, which can also be attributed to the smaller closed-shell repulsion by the nitrogen atom in ethanimine 7 than that by the oxygen atom in acetaldehyde 13. Therefore, the relative energy of transition state 8-ts is higher than that of 14-ts.

Fig. 6 Distortion, interaction, and total energies along the reaction pathways for ene-reactions (1) (black), (3) (blue), and (5) (red) calculated at the CBS-QB3 level of theory. The solid lines are the reaction energies. The dashed lines are the distortion energies. The dotted lines are the interaction energies.

The distortion, interaction, and reaction energies along the complete reaction pathways for ethylidenesilane 4, ethylidenephosphine 10, and ethanethial 16 are shown in Fig. 7. Theoretical calculations indicate that the lowest interaction energy leads to the very early transition state 5-ts. Therefore, the activation free energy for reaction (2) is much lower than that for reactions (4) and (6). The distortion energy for reaction (4) is higher than that for reaction (6), while the interaction energies show the opposite trend. Therefore, the relative free energy of transition state 11-ts is only a little lower than that of transition state 17-ts. The activation energies for reactions (2), (4), and (6) are also mainly controlled by the interaction energies. The lower interaction energy leads to an earlier transition state with a lower energy barrier.

Fig. 7 Distortion, interaction, and total energies along the reaction pathways for ene-reactions (2) (black), (4) (blue), and (6) (red) calculated at CBS-QB3 level of theory. The solid lines are the reaction energies. The dashed lines are the distortion energies. The dotted lines are the interaction energies.

Conclusions

The reactivity of uncatalyzed Alder-ene type reactions of hetero-substituted propylene was investigated using CBS-QB3, G3B3, M11, and B3LYP methods, and the results are interpreted by distortion–interaction analysis of both the transition states and the complete reaction pathways. Theoretical calculations indicate that third-period element substituted ene reactants (4, 10, and 16) are more reactive than the corresponding second-period element substituted ene reactants (1, 7, and 13), which can be attributed to the lower interaction energies along the reaction pathways for reactions (2), (4), and (6). The reactivity of the same period element substituted ene reactants is 1 > 7 > 13, and 4 > 10 > 16. Distortion–interaction analysis along the reaction pathways shows that a lower interaction energy leads to an earlier transition state and a lower reaction barrier. However, the reactivity can only be partly explained by the distortion–interaction model of the transition states.

Acknowledgements

This project was supported by the National Science Foundation of China (Grant 21372266, and 51302327), and the Foundation of Bairenjihua Chongqing University (project 0903005203191). We are also thankful for the project (No. 106112015CDJZR228806) supported by the Fundamental Research Funds for the Central Universities (Chongqing University).

Notes and references

1. (a) R. D. Brown, J. Chem. Soc., 1950, 691–697; (b) D. Biermann and W. Schmidt, J. Am. Chem. Soc., 1980, 102, 3173–3181; (c) P. A. Clark, F. Brogli and E. Heilbronner, Helv. Chim. Acta, 1972, 55, 1415–1428; (d) B. Pullman, A. Pullman and J. W. Cook, Prog. Org. Chem., 1958, 4, 31–71; (e) B. A. Hess, Jr. and L. J. Schaad, J. Am. Chem. Soc., 1971, 93, 305–310; (f) R. H. Wightman, T. M. Cresp and F. Sondheimer, J. Am. Chem. Soc., 1976, 98, 6052–6053.
2. (a) L. Salem, J. Am. Chem. Soc., 1968, 90, 543–552; (b) K. Fukui, Acc. Chem. Res., 1971, 4, 57–64; (c) K. N. Houk, Acc. Chem. Res., 1975, 8, 361–369; (d) K. N. Houk, in Pericyclic Reactions, ed. A. P. Marchand and R. E. Lehr, Academic Press, New York, 1977, vol. 2, pp. 181–271; (e) K. Fukui, Angew. Chem., Int. Ed. Engl., 1982, 21, 801–809.
3. (a) A. Matouschek and A. R. Fersht, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 7814–7818; (b) M. Solà and A. Toro-Labbé, J. Phys. Chem. A, 1999, 103, 8847–8852; (c) D. Fărcasiu, J. Chem. Educ., 1975, 52, 76–79; (d) W. J. le Noble and T. Asano, J. Am. Chem. Soc., 1975, 97, 1778–1782; (e) N. Agmon, J. Chem. Soc., Faraday Trans. 2, 1978, 74, 388–404; (f) G. A. Arteca and P. G. Mezey, J. Phys. Chem., 1989, 93, 4746–4751; (g) R. F. Nalewajski and E. Broniatowska, Chem. Phys. Lett., 2003, 376, 33–39; (h) N. M. Donahue, J. Phys. Chem. A, 2001, 105, 1489–1497; (i) G. A. Petersson, T. G. Tensfeldt and J. A. Montgomery, Jr., J. Am. Chem. Soc., 1992, 114, 6133–6138; (j) J. Cioslowski, J. Am. Chem. Soc., 1991, 113, 6756–6760; (k) G. A. Arteca and P. G. Mezey, J. Comput. Chem., 1988, 9, 728–744; (l) F. A. Bulat and A. Toro-Labbé, J. Phys. Chem. A, 2003, 107, 3987–3994.
4. (a) L. Tender, M. T. Carter and R. W. Murray, Anal. Chem., 1994, 66, 3173–3181; (b) S. J. Klippenstein, J. Chem. Phys., 1992, 96, 367–371; (c) T. M. Nahir, R. A. Clark and E. F. Bowden, Anal. Chem., 1994, 66, 2595–2598; (d) M. Chou, C. Creutz and N. Sutin, J. Am. Chem. Soc., 1977, 99, 5615–5623; (e) I.-S. H. Lee, E. H. Jeoung and M. M. Kreevoy, J. Am. Chem. Soc., 1997, 119, 2722–2728; (f) L. Eberson, Acta Chem. Scand., Ser. B, 1982, 36, 533–543; (g) M. M. Kreevoy and I.-S. H. Lee, J. Am. Chem. Soc., 1984, 106, 2550–2553; (h) L. Eberson, Acta Chem. Scand., Ser. B, 1984, 38, 439–459; (i) J. A. Dodd and J. I. Brauman, J. Phys. Chem., 1986, 90, 3559–3562; (j) J. M. Mayer, Acc. Chem. Res., 2011, 44, 36–46; (k) C. J. Schlesener, C. Amatore and J. K. Kochi, J. Am. Chem. Soc., 1984, 106, 7472–7482.
5. (a) D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198; (b) F. Liu, R. S. Paton, S. Kim, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 15642–15649; (c) R. Rajeev and R. B. Sunoj, J. Org. Chem., 2013, 78, 7023–7029; (d) C. A. Sader and K. N. Houk, ARKIVOC, 2014, 3, 170–183; (e) S. I. Gorelsky, Organometallics, 2012, 31, 794–797; (f) M. García-Melchor, S. I. Gorelsky and T. K. Woo, Chem.–Eur. J., 2011, 17, 13847–13853; (g) C. Y. Legault, Y. Garcia, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 12664–12665; (h) S. Potavathri, K. C. Pereira, S. I. Gorelsky, A. Pike, A. P. LeBris and B. DeBoef, J. Am. Chem. Soc., 2010, 132, 14676–14681; (i) S. I. Gorelsky, D. Lapointe and K. Fagnou, J. Am. Chem. Soc., 2008, 130, 10848–10849; (j) S. I. Gorelsky, D. Lapointe and K. Fagnou, J. Org. Chem., 2012, 77, 658–668; (k) D. H. Ess, W. A. Goddard III and R. A. Periana, Organometallics, 2010, 29, 6459–6472; (l) M. Stępień, J. Org. Chem., 2013, 78, 9512–9516.
6. (a) K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325–340; (b) S. Nagase and K. Morokuma, J. Am. Chem. Soc., 1978, 100, 1666–1672; (c) R. D. J. Froese, J. M. Coxon, S. C. West and K. Morokuma, J. Org. Chem., 1997, 62, 6991–6997; (d) N. Koga, T. Ozawa and K. Morokuma, J. Phys. Org. Chem., 1990, 3, 519–533; (e) J. M. Coxon, S. T. Grice, R. G. A. R. Maclagan and D. Q. McDonald, J. Org. Chem., 1990, 55, 3804–3807; (f) J. M. Coxon, R. D. J. Froese, B. Ganguly, A. P. Marchand and K. Morokuma, Synlett, 1999, 1681–1703; (g) M. Avalos, R. Babiano, J. L. Bravo, P. Cintas, J. L. Jiménez, J. C. Palacios and M. A. Silva, J. Org. Chem., 2000, 65, 6613–6619; (h) K. Geetha, T. C. Dinadayalane and G. N. Sastry, J. Phys. Org. Chem., 2003, 16, 298–305; (i) M. Manoharan and P. Venuvanalingam, J. Chem. Soc., Perkin Trans. 2, 1996, 1423–1427; (j) K. Kavitha, M. Manoharan and P. Venuvanalingam, J. Org. Chem., 2005, 70, 2528–2536; (k) K. Kavitha and P. Venuvanalingam, Int. J. Quantum Chem., 2005, 104, 64–78; (l) P. Blowers, L. Ford and R. Masel, J. Phys. Chem. A, 1998, 102, 9267–9277.
7. K. N. Houk, R. W. Gandour, R. W. Strozier, N. G. Rondan and L. A. Paquette, J. Am. Chem. Soc., 1979, 101, 6797–6802.
8. (a) F. M. Bickelhaupt, J. Comput. Chem., 1999, 20, 114–128; (b) G. T. Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967; (c) A. Diefenbach and F. M. Bickelhaupt, J. Chem. Phys., 2001, 115, 4030–4040; (d) A. Diefenbach and F. M. Bickelhaupt, J. Phys. Chem. A, 2004, 108, 8460–8466; (e) A. Diefenbach and F. M. Bickelhaupt, J. Organomet. Chem., 2005, 690, 2191–2199; (f) A. Diefenbach, G. T. de Jong and F. M. Bickelhaupt, Mol. Phys., 2005, 103, 995–998; (g) A. Diefenbach, G. T. de Jong and F. M. Bickelhaupt, J. Chem. Theory Comput., 2005, 1, 286–298; (h) J. N. P. van Stralen and F. M. Bickelhaupt, Organometallics, 2006, 25, 4260–4268; (i) G. T. de Jong, R. Visser and F. M. Bickelhaupt, J. Organomet. Chem., 2006, 691, 4341–4349; (j) G. T. de Jong and F. M. Bickelhaupt, ChemPhysChem, 2007, 8, 1170–1181; (k) G. T. de Jong and F. M. Bickelhaupt, J. Chem. Theory Comput., 2007, 3, 514–529.
9. (a) P.-O. Norrby, H. C. Kolb and K. B. Sharpless, Organometallics, 1994, 13, 344–347; (b) M. Boronat, P. Viruela and A. Corma, J. Phys. Chem. B, 1999, 103, 7809–7821; (c) E. Kelly, M. Seth and T. Ziegler, J. Phys. Chem. A, 2004, 108, 2167–2180.
10. Ziegler and Rauk have considered distortion energy as part of their extended transition state method: (a) T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10; (b) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558–1565; (c) F. M. Bickelhaupt, T. Ziegler and P. von Ragué Schleyer, Organometallics, 1995, 14, 2288–2296.
11. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646–10647.
12. Y. Lan, S. E. Wheeler and K. N. Houk, J. Chem. Theory Comput., 2011, 7, 2104–2111.
13. S. Liu, Y. Lei, X. Qi and Y. Lan, J. Phys. Chem. A, 2014, 118, 2638–2645.
14. (a) K. Alder, F. Pascher and A. Schmitz, Chem. Ber., 1943, 76B, 27–53; (b) K. Alder and T. Noble, Chem. Ber., 1943, 76B, 54–57; (c) K. Alder and C.-H. Schmidt, Chem. Ber., 1943, 76B, 183–205.
15. (a) H. M. R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 8, 556–577; (b) B. B. Snider, Acc. Chem. Res., 1980, 13, 426–432; (c) J. Dubac and A. Laporterie, Chem. Rev., 1987, 87, 319–334; (d) K. Mikami and M. Shimizu, Chem. Rev., 1992, 92, 1021–1050; (e) B. B. Snider, in Comprehensive Organic Synthesis, ed. B. M. Trost and I. Fleming, Pergamon Press, New York, 1991, vol. 5, pp. 1–27; (f) T. Okachi, K. Fujimoto and M. Onaka, Org. Lett., 2002, 4, 1667–1669; (g) A. Corma and M. Renz, Chem. Commun., 2004, 5, 550–551; (h) Q. Xia and B. Ganem, Org. Lett., 2001, 3, 485–487.
16. (a) A. Lei, J. P. Waldkirch, M. He and X. Zhang, Angew. Chem., Int. Ed., 2002, 41, 4526–4529; (b) J. P. Hartley and S. G. Pyne, Synlett, 2004, 2209–2211; (c) A. L. Lehmann, A. C. Willis and M. G. Banwell, Aust. J. Chem., 2010, 63, 1665–1678; (d) D. Strübing, H. Neumann, S. Hübner, S. Klaus and M. Beller, Tetrahedron, 2005, 61, 11345–11354; (e) R. V. Ashirov, S. A. Appolonova, G. A. Shamov and V. V. Plemenkov, Mendeleev Commun., 2006, 16, 276–278; (f) M. C. Slade and J. S. Johnson, Beilstein J. Org. Chem., 2013, 9, 166–172; (g) A. Giannis, P. Heretsch, V. Sarli and A. StÖßel, Angew. Chem., Int. Ed., 2009, 48, 7911–7914; (h) F. Liu, Q. Liu, M. He, X. Zhang and A. Lei, Org. Biomol. Chem., 2007, 5, 3531–3534; (i) B. M. Trost, A. B. Pinkerton, F. D. Toste and M. Sperrle, J. Am. Chem. Soc., 2001, 123, 12504–12509; (j) E. C. Hansen and D. Lee, J. Am. Chem. Soc., 2006, 128, 8142–8143; (k) K. Närhi, J. Franzén and J.-E. Bäckvall, J. Org. Chem., 2006, 71, 2914–2917; (l) E. O. Onyango and P. A. Jacobi, J. Org. Chem., 2012, 77, 7411–7427; (m) G. Hilt, A. Paul and J. Treutwein, Org. Lett., 2010, 12, 1536–1539; (n) D. M. Hodgson, E. P. A. Talbot and B. P. Clark, Org. Lett., 2011, 13, 2594–2597; (o) K. M. Brummond and B. Mitasev, Org. Lett., 2004, 6, 2245–2248; (p) B. M. Trost and A. Martos-Redruejo, Org. Lett., 2009, 11, 1071–1074.
17. (a) R. Koch, J. J. Finnerty, S. Murali and C. Wentrup, J. Org. Chem., 2012, 77, 1749–1759; (b) X. Lu, Org. Lett., 2004, 6, 2813–2815; (c) K. Chakrabarty, S. Roy and G. K. Das, J. Mol. Struct.: THEOCHEM, 2008, 858, 107–112; (d) A. G. Leach and K. N. Houk, Org. Biomol. Chem., 2003, 1, 1389–1403; (e) A. G. Leach and K. N. Houk, Chem. Commun., 2002, 12, 1243–1255; (f) K. N. Houk, J. C. Williams, Jr., P. A. Mitchell and K. Yamaguchi, J. Am. Chem. Soc., 1981, 103, 949–951; (g) M. L. Clarke and M. B. France, Tetrahedron, 2008, 64, 9003–9031; (h) S. S.-M. Choi, G. W. Kirby and M. P. Mahajan, J. Chem. Soc., Chem. Commun., 1990, 2, 138–140.
18. (a) L. Yuan, Q. Hu, Q. Yang and W. Zhang, Comput. Theor. Chem., 2013, 1019, 71–77; (b) Q. Yang, Y. Liu and W. Zhang, Org. Biomol. Chem., 2011, 9, 6343–6351; (c) W. Adam, H.-G. Brünker, A. S. Kumar, E.-M. Peters, K. Peters, U. Schneider and H. G. von Schnering, J. Am. Chem. Soc., 1996, 118, 1899–1905; (d) Y. Naruse, T. Suzuki and S. Inagaki, Tetrahedron Lett., 2005, 46, 6937–6940; (e) Q. Yang, X. Tong and W. Zhang, J. Mol. Struct.: THEOCHEM, 2010, 957, 84–89.
19. (a) L. M. Stephenson, M. J. Grdina and M. Orfanopoulos, Acc. Chem. Res., 1980, 13, 419–425; (b) W. Adam and O. Krebs, Chem. Rev., 2003, 103, 4131–4146.
20. (a) R. J. Loncharich, T. R. Schwartz and K. N. Houk, J. Am. Chem. Soc., 1987, 109, 14–23; (b) B. E. Thomas IV, R. J. Loncharich and K. N. Houk, J. Org. Chem., 1992, 57, 1354–1362; (c) G. D. Paderes and W. L. Jorgensen, J. Org. Chem., 1992, 57, 1904–1916; (d) O. Achmatowicz and E. Bialecka-Florjańcyzk, Tetrahedron, 1996, 52, 8827–8834; (e) K. N. Houk, B. R. Beno, M. Nendel, K. Black, H. Y. Yoo, S. Wilsey and J. K. Lee, J. Mol. Struct., 1997, 398, 169–179.
21. B. B. Snider and E. Ron, J. Am. Chem. Soc., 1985, 107, 8160–8164.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, GAUSSIAN 09 (Revision D. 01), Gaussian, Wallingford, CT, 2013.
23. (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789; (c) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627; (d) C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
24. (a) B. J. Lynch, P. L. Fast, M. Harris and D. G. Truhlar, J. Phys. Chem. A, 2000, 104, 4811–4815; (b) Y. Zhao, O. Tishchenko and D. G. Truhlar, J. Phys. Chem. B, 2005, 109, 19046–19051; (c) S. Tsuzuki and H. P. Lüthi, J. Chem. Phys., 2001, 114, 3949–3957; (d) J. A. Duncan and M. C. Spong, J. Phys. Org. Chem., 2005, 18, 462–467; (e) M. D. Wodrich, C. Corminboeuf and P. von Ragué Schleyer, Org. Lett., 2006, 8, 3631–3634.
25. R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817.
26. (a) R. Peverati and D. G. Truhlar, Phys. Chem. Chem. Phys., 2012, 14, 16187–16191; (b) H. M. Jonkers, S. de Bruin and H. van Gemerden, Microb. Ecol., 1998, 27, 281–290.
27. J. A. Montgomery, Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 1999, 110, 2822–2827.
28. (a) M. R. Nyden and G. A. Petersson, J. Chem. Phys., 1981, 75, 1843–1862; (b) G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090; (c) G. A. Petersson, D. K. Malick, W. G. Wilson, J. W. Ochterski, J. A. Montgomery, Jr. and M. J. Frisch, J. Chem. Phys., 1998, 109, 10570–10579; (d) J. A. Montgomery, Jr., M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112, 6532–6542.
29. (a) D. H. Ess and K. N. Houk, J. Phys. Chem. A, 2005, 109, 9542–9553; (b) J. W. Ochterski, G. A. Petersson and J. A. Montgomery, Jr., J. Chem. Phys., 1996, 104, 2598–2619.
30. A. G. Baboul, L. A. Curtiss, P. C. Redfern and K. Raghavachari, J. Chem. Phys., 1999, 110, 7650–7657.
31. (a) J. A. Pople, M. Head-Gordon, D. J. Fox, K. Raghavachari and L. A. Curtiss, J. Chem. Phys., 1989, 90, 5622–5629; (b) L. A. Curtiss, C. Jones, G. W. Trucks, K. Raghavachari and J. A. Pople, J. Chem. Phys., 1990, 93, 2537–2545; (c) L. A. Curtiss, K. Raghavachari, G. W. Trucks and J. A. Pople, J. Chem. Phys., 1991, 94, 7221–7230; (d) L. A. Curtiss, K. Raghavachari, P. C. Redfern, V. Rassolov and J. A. Pople, J. Chem. Phys., 1998, 109, 7764–7776.
32. (a) X.-M. Meng, L.-F. Zou, M. Xie and Y. Fu, Chin. J. Chem., 2008, 26, 787–793; (b) Y. Feng, L. Liu, J.-T. Wang, S.-W. Zhao and Q.-X. Guo, J. Org. Chem., 2004, 69, 3129–3138; (c) K. Range, D. Riccardi, Q. Cui, M. Elstner and D. M. York, Phys. Chem. Chem. Phys., 2005, 7, 3070–3079; (d) B. Anantharaman and C. F. Melius, J. Phys. Chem. A, 2005, 109, 1734–1747.
33. (a) M. J. Aurell, L. R. Domingo, P. Pérez and R. Contreras, Tetrahedron, 2004, 60, 11503–11509; (b) F. Méndez, J. Tamariz and P. Geerlings, J. Phys. Chem. A, 1998, 102, 6292–6296; (c) R. Herrera, A. Nagarajan, M. A. Morales, F. Méndez, H. A. Jiménez-Vázquez, L. G. Zepeda and J. Tamariz, J. Org. Chem., 2001, 66, 1252–1263; (d) M. Carda, R. Portolés, J. Murga, S. Uriel, J. A. Marco, L. R. Domingo, R. J. Zaragozá and H. Röper, J. Org. Chem., 2000, 65, 7000–7009; (e) L. R. Domingo, Eur. J. Org. Chem., 2000, 12, 2265–2272; (f) D. H. Ess, G. O. Jones and K. N. Houk, Adv. Synth. Catal., 2006, 348, 2337–2361; (g) L. R. Domingo, J. Org. Chem., 1999, 64, 3922–3929.
34. (a) K. Fukui, J. Chem. Phys., 1970, 74, 4161–4163; (b) K. Ishida, K. Morokuma and A. Komornicki, J. Chem. Phys., 1977, 66, 2153–2156.
35. (a) A. M. Sarotti, Org. Biomol. Chem., 2014, 12, 187–199; (b) Y. Li, X. Qi, Y. Lei and Y. Lan, RSC Adv., 2015, 5, 49802–49808; (c) I. Fernández and F. M. Bickelhaupt, J. Comput. Chem., 2012, 33, 509–516; (d) A. G. Green, P. Liu, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 4575–4583; (e) F. Liu, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 11483–11493; (f) D. H. Ess, J. Org. Chem., 2009, 74, 1498–1508.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra10345b

‡ Rui Jin and Song Liu contributed equally to this work.

---