Orientation dependence of the pseudo-Hall effect in p-type 3C–SiC four-terminal devices under mechanical stress†
Hoang-Phuong Phan‡
*a,
Afzaal Qamar‡a,
Dzung Viet Daoab,
Toan Dinha,
Li Wanga,
Jisheng Hana,
Philip Tannera,
Sima Dimitrijevab and
Nam-Trung Nguyen a
a
aQueensland Micro-Nanotechnology Centre, Griffith University, Queensland, Australia. E-mail: hoangphuong.phan@griffithuni.edu.au
bSchool of Engineering, Griffith University, Queensland, Australia
First published on 22nd June 2015
Abstract
This paper presents for the first time the orientation dependence of the pseudo-Hall effect in p-type 3C–SiC four-terminal devices under mechanical stress. Experimental results indicate that the offset voltage of p-type 3C–SiC four-terminal devices significantly depends on the directions of the applied current and stress. We also calculated the piezoresistive coefficients π61, π62, and π66, showing that π66 with its maximum value of approximately 16.7 × 10−11 Pa−1 plays a more dominant role than π61 and π62. The magnitude of the offset voltage in arbitrary orientation under stress was estimated based on these coefficients. The finding in this study plays an important role in the optimization of Microelectromechanical Systems (MEMS) mechanical sensors utilizing the pseudo-Hall effect in p-type 3C–SiC.
Silicon Carbide (SiC), with its large energy band gap (2.3–3.4 eV) and superior mechanical properties, is an excellent candidate for electrical devices operating in harsh environments.1–5 Recent studies have paid significant attention to the characterization of the strain effect on SiC for sensing applications under hostile conditions.6–8 Many groups have reported the piezoresistive effect in various poly types of SiC such as 3C–SiC, 4H–SiC, and 6H–SiC. Large gauge factors of approximately 30 were reported in both p-type and n-type single crystalline SiC, indicating that SiC has high potential for mechanical sensing applications.9–14 Among more than 200 poly types of crystalline SiC, cubic crystalline silicon carbide (3C–SiC) is preferable for Microelectromechanical systems (MEMS) transducers. The main advantage of 3C–SiC over other poly types is the capability of growth on a silicon (Si) substrate, which reduces the cost of wafers and is more compatible with the conventional MEMS process.2,12–15 Most previous studies on the piezoresistive effect of SiC utilized the conventional two-terminal resistors requiring a Wheatstone bridge for voltage read-out,15,16 which faces several drawbacks. For instance, the four resistors in the bridge must be closely identical to obtain a zero offset.17–19 In addition, the resistors in the Wheatstone bridge must have almost the same temperature coefficient to avoid the offset drift due to the change of temperature.20 Compared to two-terminal resistors, four-terminal devices have proved to be more thermally stable and suitable for the miniaturization of sensors, since they do not require any external Wheatstone bridge.17–21 Under a mechanical shear strain, a voltage is generated across two terminals of four-terminal devices due to the distortion of potential distribution, and this phenomenon has been named as the pseudo-Hall effect.22,23 To date, there have been various studies on the pseudo-Hall effect in silicon material, and in fact this effect in Si has been utilized in commercial strain sensors for more than two decades.23,24 However, the work on the pseudo-Hall effect in SiC has been rarely reported.25 As the pseudo-Hall effect in semiconductors depends on the crystallography orientation, it is important to investigate which orientation offers the most significant effect in 3C–SiC four-terminal devices.
In this paper, we report on the orientation dependence of the pseudo-Hall effect in p-type 3C–SiC thin films. The piezoresistive coefficients, π61, π62, and π66, which define the magnitude of the pseudo-Hall effect were also investigated. The insight gained in this study is vital to the development of MEMS mechanical sensors using the pseudo-Hall effect in 3C–SiC.
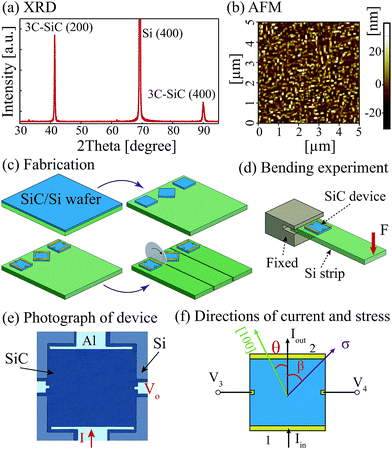
The 3C–SiC thin films were grown on (100) Si substrate using low pressure chemical vapor deposition (LPCVD)26 at a low temperature of 1000 °C. The alternating supply epitaxy approach was used to achieve single crystalline SiC film deposition with silane (SiH4) and propylene (C3H6) as precursors. Aluminum was employed as the dopant in the in situ doping process where trimethylaluminum [(CH3)3Al, TMAl] was the precursor to form p-type 3C–SiC. The properties of the grown single crystalline 3C–SiC films were characterized and reported elsewhere.26,27 The X-ray diffraction (XRD) measurement indicated that the SiC film is epitaxially grown on Si (100) substrate, Fig. 1(a). Based on the X-ray photoelectron spectroscopy data, the atomic concentrations of carbon and silicon were found to be approximately 52.9% and 47.1%, respectively, while that of aluminum was below 1%. The atomic force microscopy (AFM) image of a 380 nm 3C–SiC film shows that the roughness of a 5 μm × 5 μm area was 20 nm, Fig. 1(b). The semiconductor type and carrier concentration of the films were then investigated using the hot probe method.28 The positive voltage at the hot probe indicated the 3C–SiC film was p-type semiconductor, and the carrier concentration was calculated to be in the range of 1018 cm−3. Fig. 1(c) shows the fabrication of the 3C– SiC four-terminal device using a 2-masks-photolithography process. In the first step, SiC pattern was formed using Inductively Coupled Plasma (ICP) etching with an etch-rate of approximately 200 nm min−1.27 Next, aluminum was deposited on the SiC film using sputtering, and aluminum electrodes were then patterned using wet etching. Finally, the SiC/Si wafers were diced into smaller strips with dimensions of 9 mm × 60 mm × 0.6 mm for the subsequent bending experiment, Fig. 1(d). A photograph of the fabricated devices and a schematic sketch of the current and applied stress are shown in Fig. 1(e) and (f).
The linear current–voltage characteristics of the SiC four-terminal devices were measured using ™HP4145B, indicating a good Ohmic contact between the aluminum electrodes and the p-type 3C–SiC films. The current leakage between the 3C–SiC layer and the Si substrate was also investigated to ensure that Si substrate did not contribute to the measured results (see the ESI†). To characterize the pseudo-Hall effect in the four-terminal SiC devices, we applied stress to the SiC films using the bending beam method, while supplying a constant current through terminals 1 and 2 and monitoring the change of the generated voltage across terminal 3 and 4 of the SiC devices, Fig. 1(d) and (f). Since the thickness of the SiC films (∼300 nm) is less than 0.1% of that of the Si substrate (600 μm), we assumed that the strain induced into the SiC films is approximately equal to that of the surface of the Si substrate: ε = Mt/2ESiI, where M is the bending moment; I is the moment of inertia; ESi and t are the Young's modulus and the thickness of the Si layer, respectively. Accordingly, for an applied load varied from 0 to 2 N to the free end of the Si strips, the strain induced into the SiC layer was in a range of 0 to 900 ppm. The stress applied to the SiC layer (σSiC) was then calculated using Hooke's law: σSiC = ESiCε, where ESiC is the Young's modulus of 3C–SiC.29
We investigated the orientation dependence of the pseudo-Hall effect of p-type 3C–SiC thin films by characterizing SiC four-terminal devices aligned in different directions and being stressed in different orientations, as summarized in Table 1. Fig. 2 shows that for sample A (the orientation of the current is [100], and the direction of the stress is [110]), an offset voltage was generated across terminals 3 and 4 when we applied a stress in [110] orientation. It is also clear that, the offset voltage increased when increasing the applied stress to 264 MPa. The offset voltage then decreased with decreasing the stress, and returned to 0 when the load was completely removed. The generated voltage of the SiC four-terminal resistors under stress was measured for several testing cycles, showing a good reproducibility without any significant drift voltage (see ESI†). This indicates the feasibility of using the pseudo-Hall effect in p-type 3C–SiC four-terminal devices for MEMS strain/stress sensors.
| Test samples | Orientation of current | Orientation of uniaxial stress | θ | β |
|---|---|---|---|---|
| a θ is the angle between the direction of the applied current and [100] orientation, and β is the angle between the directions of the applied stress and the current in 3C–SiC (100) plane. | ||||
| A | [100] | [110] | 0° | 45° |
| B | [110] | [110] | 45° | 0° |
| C | [110] | [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] 0] |
45° | 90° |
| D | [110] | [100] | 45° | 45° |
| E | [100] | [100] | 0° | 0° |
| F | [100] | [010] | 0° | 90° |
The same phenomenon was also observed in other samples (B, C, D, E, F), but with different order of magnitude. Fig. 3 shows the ratio of the output voltage to the input voltages of different samples A, B, C, D, E and F, indicating a linear relationship between the output offset voltage (Vout/Vin) and applied stress (σ). These results also show that the magnitude of the generated offset voltage in 3C–SiC four-terminal devices varies with the directions of the current and the applied stress, indicating the orientation dependence of the pseudo-Hall effect in p-type 3C–SiC thin film. As 3C–SiC has the cubic crystalline structure like Si, we qualitatively and quantitatively explained the pseudo-Hall effect and its orientation dependence in p-type 3C–SiC, using the model proposed by Kanda et al. for the case of Si.17,30 Fig. 3 (inset) shows an equivalent circuit of the four-terminal device, which consists of four resistors R13, R14, R23, and R24. In the strain-free state, these four resistors are considered to be identical (R13 = R14 = R23 = R24). Under a uniaxial mechanical strain as shown in Fig. 1(d), these four resistors are stressed, and their resistances change. As R13, R14, R23, and R24 are aligned in different orientations, these resistance changes are different, leading to an unbalance of the bridge circuit, which results in a non-zero voltage across terminals 3 and 4. The ratio of the generated voltage (Vout) across terminals 3 and 4 to the applied voltage across terminals 1 and 2 (Vin) due to stress can be quantified by the coefficients π61, π62, and π66, as expressed in the following equation (see the ESI†) 33,34:
| Vout = Vin (π61σ1 + π62σ2 + π66σ6) | (1) |
 | (2) |
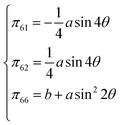 | (3) |
 | ||
| Fig. 3 The ratio of the generated voltage and applied voltage of the SiC four-terminal devices aligned in different orientation. Inset: the equivalent four resistors R13, R14, R23, and R24 of a 3C–SiC four-terminal device.32 | ||
 | ||
| Fig. 4 (a) The coefficients π61, π62, and π66 of SiC four-terminal devices when θ varies from 0 to π; (b) π61 and π62 are plotted in a different scale. | ||
Based on the coefficients, we estimated the magnitude of the output offset voltage of 3C–SiC four-terminal devices under stress for MEMS mechanical sensors. Substituting eqn (2) into eqn (1), and using the calculated piezoresistive coefficients shown in Fig. 4, it is possible to theoretically estimate the magnitude of the pseudo-Hall effect of 3C–SiC four-terminal devices aligned in arbitrary orientations. Fig. 5 shows the ratio of the generated voltage to the applied voltage per unit applied stress ([Vout/Vin]/σ). It is obvious that, the magnitude of the effect in p-type 3C–SiC varies with orientations of current and stress. Accordingly, in (100) plane, the absolute offset voltage (|Vout|) gains its maximum value when (θ, β) = (mπ/2, (2n + 1)π/4), where m and n are integers. Therefore, when designing MEMS mechanical sensors using the pseudo-Hall effect in p-type 3C–SiC four-terminal resistor, these orientations should be chosen to enhance the sensitivity of sensors. On the other hand, for the Hall-devices where a constant offset voltage under external stress is desired, the orientations of (θ, β) = (mπ/4, nπ/2) should be selected to minimize the pseudo-Hall effect (here m and n are integers).
 | ||
| Fig. 5 The ratio of the generated voltage across terminals 3 and 4 to the input voltage across terminals 1 and 2 per unit uniaxial stress σ. | ||
In conclusion, we reported on the pseudo-Hall effect in p-type 3C–SiC four-terminal devices, the orientation dependence, and piezoresistive coefficients π61, π62, and π66. The maximum value of π66 was found to be 16.7 × 10−11 Pa−1, while that of π61 and π62 was 3.7 × 10−11 Pa−1, implying that π66 plays a more dominant role than the other coefficients. Based on these piezoresistive coefficients, it is possible to estimate the magnitude of the pseudo-Hall effect in any arbitrary orientation. Furthermore, the large output voltage at a certain applied current and stress along with a direct/simple signal-readout method indicate that pseudo-Hall effect in p-type 3C–SiC is a good candidate for MEMS applications. These findings in this study play an important role in designing/optimizing MEMS mechanical sensors as well as Hall devices utilizing p-type 3C–SiC material.
This work was performed in part at the Queensland node of the Australian National Fabrication Facility, a company established under the National Collaborative Research Infrastructure Strategy to provide nano and micro-fabrication facilities for Australia's researchers. This work has been partially supported by the Griffith University's New Researcher Grants.
References
- P. M. Sarro, Sens. Actuators, A, 2000, 82(1–3), 210 CrossRef CAS.
- M. Mehregany, C. A. Zorman, N. Rajan and C. H. Wu, Proc. IEEE, 1998, 86(8), 1594 CrossRef CAS.
- X. Zhang, Y. Chen, W. Liu, W. Xue, J. Li and Z. Xie, J. Mater. Chem. C, 2013, 1, 6479–6486 RSC.
- (a) S. Chen, P. Ying, L. Wang, F. Gao, G. Wei, J. Zheng, Z. Xie and W. Yang, RSC Adv., 2014, 4(16), 8376–8382 RSC; (b) S. Chen, P. Ying, L. Wang, G. Wei, J. Zheng, F. Gao, S. Su and W. Yang, J. Mater. Chem. C, 2013, 1(31), 4779–4784 RSC.
- (a) S. Chen, P. Ying, L. Wang, G. Wei, F. Gao, J. Zheng, M. Shang, Z. Yang, W. Yang and T. Wu, NPG Asia Mater., 2015, 7(1), e157 CrossRef CAS PubMed; (b) S. Chen, P. Ying, L. Wang, G. Wei and W. Yang, Appl. Phys. Lett., 2014, 105(13), 133106 CrossRef PubMed.
- A. Qamar, P. Tanner, D. V. Dao, H. P. Phan and T. Dinh, IEEE Electron Device Lett., 2014, 35(12), 1293–1295 CrossRef CAS.
- J. Bi, G. Wei, L. Wang, F. Gao, J. Zheng, B. Tang and W. Yang, J. Mater. Chem. C, 2013, 1, 4514 RSC.
- F. Gao, J. Zheng, M. Wang, G. Wei and W. Yang, Chem. Commun., 2011, 47, 11993 RSC.
- R. Shao, K. Zheng, Y. Zhang, Y. Li, Z. Zhang and X. Han, Appl. Phys. Lett., 2012, 101, 233109 CrossRef PubMed.
- T. Akiyama, D. Briand and N. F. Rooij, J. Micromech. Microeng., 2012, 22, 085034 CrossRef.
- R. S. Okojie, A. A. Ned, A. D. Kurtz and W. N. Carr, IEEE Trans. Electron Devices, 1998, 45(4), 785 CrossRef CAS.
- H. P. Phan, P. Tanner, D. V. Dao, N. T. Nguyen, L. Wang, Y. Zhu and S. Dimitrijev, IEEE Electron Device Lett., 2014, 35(3), 399 CrossRef CAS.
- H. P. Phan, D. V. Dao, P. Tanner, N. T. Nguyen, J. S. Han, S. Dimitrijev, G. Walker, L. Wang and Y. Zhu, J. Matter. Chem. C, 2014, 2, 7176–7179 RSC.
- J. S. Shor, D. Goldstein and A. D. Kurtz, IEEE Trans. Electron Devices, 1993, 40(6), 1093 CrossRef CAS.
- H. P. Phan, D. V. Dao, L. Wang, T. Dinh, N. T. Nguyen, A. Qamar, P. Tanner, S. Dimitrijev and Y. Zhu, J. Mater. Chem. C, 2015, 3, 1172–1176 RSC.
- C. H. Wu, C. A. Zorman and M. Mehregany, IEEE Sensors. J., 2006, 6(2), 316 CrossRef CAS.
- Y. Kanda, Jpn. J. Appl. Phys., 1987, 26(7R), 1031 CrossRef CAS.
- A. V. Gridchin and V. A. Gridchin, Sens. Actuators, A, 1997, 58(3), 219–223 CrossRef CAS.
- A. Mian, J. C. Suhling and R. C. Jaeger, The van der pauw stress sensor, IEEE Sensors. J., 2006, 6(2), 340–356 CrossRef.
- M. Doelle, D. Mager, P. Ruther and O. Paul, Sens. Actuators, A, 2006, 127(2), 261–269 CrossRef CAS PubMed.
- R. C. Jaeger, M. Motalab, S. Hussain and J. C. Suhling, J. Electron. Packag., 2014, 136(4), 041014 CrossRef.
- S. Yue, W. A. Moussa and L. R. Williston, Appl. Phys. A, 2014, 116(2), 409–414 CrossRef CAS.
- J. C. Doll and B. L. Pruitt, Piezoresistor design and applications, Springer, 2013, ISBN 978-1-4614-8516-2 Search PubMed.
- J. J. E. Gragg, Silicon pressure sensor, US Pat., 4,317,126,23, 1982 Search PubMed.
- A. Qamar, H.-P. Phan, D. V. Dao, P. Tanner, T. Dinh, L. Wang and S. Dimitrijev, IEEE Electron Device Lett., 2015 DOI:10.1109/LED.2015.2435153.
- L. Wang, S. Dimitrijev, P. Tanner and J. Zou, Appl. Phys. Lett., 2009, 94, 181909 CrossRef PubMed.
- Y. Wang, S. Li, J. Han, W. Wen, H. Wang, S. Dimitrijev and S. Zhang, RSC Adv., 2014, 4(97), 54441–54446 RSC.
- P. Tanner, L. Wang, S. Dimitrijev, J. Han, A. Iacopi, L. Hold and G. Walker, Sci. Adv. Mater., 2014, 6(7), 1542–1547 CrossRef CAS PubMed.
- F. Iacopi, G. Walker, L. Wang, L. Malesys, S. Ma, B. V. Cunning and A. Iacopi, Appl. Phys. Lett., 2013, 102, 011908 CrossRef PubMed.
- Y. Kanda, IEEE Trans. Electron Devices, 1982, 29(1), 64–70 CrossRef PubMed.
- W. G. Pfann and R. N. Thurston, J. Appl. Phys., 1961, 32(10), 2008–2019 CrossRef PubMed.
- Y. Kanda and M. Migitaka, Phys. Status Solidi A, 1976, 35(2), K115–K118 CrossRef CAS PubMed.
- Y. Kanda and K. Yamamura, Sens. Actuators, A, 1989, 183, 247–257 CrossRef.
- D. V. Dao, T. Toriyama, J. Wells and S. Sugiyama, Sens. Mater., 2002, 15, 113–135 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra10144a |
| ‡ Hoang-Phuong Phan and Afzaal Qamar share equal contribution to this article. |
| This journal is © The Royal Society of Chemistry 2015 |