Crystallographic, optical and dielectric properties of gel grown praseodymium malonate single crystals

Abstract

Single crystals of praseodymium malonate hexahydrate are grown by gel encapsulation technique. Single and powder X-ray diffraction data obtained on these crystals is analysed and the internal structure and molecular configuration are determined. The analysis of the crystallographic data shows that the compound crystallises in a monoclinic crystal system with a space group of P2/m. The compound adopts an extended 3-D framework, stabilized by extensive hydrogen bonding. High resolution X-ray diffraction results suggest that the crystals grown are of good quality. The optical characteristics, as obtained from UV-Vis-NIR spectral data, are described. The direct forbidden energy band gap is calculated to be 5.4 eV. Results of photoluminescence, refractive index and birefringence measurements are described and discussed. It is shown that the material has a low dielectric constant and so can be a promising material for microelectronic device applications. The dependence of the dielectric constant, dielectric loss and conductivity on the frequency of the applied ac field is described and discussed. The results are correlated with those of optical and high resolution X-ray diffraction.

---

1. Introduction

Malonates of rare earth elements are an interesting and fascinating subject of research in materials science. Malonates are salts of malonic acid; the latter being the next higher homologue of oxalic acid. The malonate ligand exhibits a flexible stereochemistry and a variable mode of binding with metal ions in the crystalline state.^1–4 A non-radiative intra-molecular energy transfer process occurs in those materials, which consist of co-ordination compounds of rare earth ions, usually trivalent (Pr³⁺), with organic ligands (malonic acid). Due to antenna effect these materials have potential applications in new technologies, such as efficient phosphors, fluorescence, photosensitive bio-inorganic compounds, and high technology optics, and they are a fundamental step for high emission quantum yields.

To the author’s best knowledge, there is no report to date regarding the crystallinity, optical and dielectric characteristics of praseodymium malonate single crystals. The previous crystallographic data published in the literature^5–7 is different from that reported here, with the reliability index factor R in the data presented here being far more accurate.

2. Experimental

The chemicals used in the present investigation include praseodymium chloride hexahydrate (99.99%) of Chengdu Haoxuan Technology Co. Ltd China, sodium metasilicate (99.50%) from Thomas Baker, Mumbai, India and L-tartratic acid (99.0%) from Loba-Chemie Indoaustranal Co., Mumbai, India. The crystallisation apparatus used for the growth of the single crystals of praseodymium malonate hexahydrate (hereafter called as PMH) by a silica gel method involves the use of a borosilicate glass tube of length 20 cm and inner diameter 2.5 cm as the crystalliser. The gel solution consisting of sodium meta silicate and malonic acid and adjusted to a particular pH value was then transferred to several crystallisers. It takes around 24 hours for the gel to set in summer (35–40 °C) whereas in winter (temperature in the range of around 10–20 °C), it takes a couple of weeks depending upon the pH value and molarity of the sodium meta silicate gel. After the gel became set, an aqueous solution of PrCl₃ of the desired molarity was gently poured along the sides of the crystalliser, so as to avoid any gel breakage. In order to conduct experiments to study the effect of the surrounding temperature on the growth of the crystals, the tubes were placed in a thermostatically controlled water bath, wherein the surrounding temperature was maintained at a constant for each experiment, ranging from 30–60 °C. A temperature > 40 °C led to Liesegang ring formation and poor quality crystals. The diffusion of Pr³⁺ ions through the narrow pores of the silica gel (gel matrix) leads to the reaction between these ions, present in the upper reactant (UR), and the (C₃H₂O₄)²⁻ ions present in the gel, as the lower reactant (LR). The following reaction results in the crystallisation of Pr malonate crystals.

2PrCl₃ + 3CH₂(COOH)₂ → Pr₂(C₃H₂O₄)₃ + 6HCl.

The morphologies of the grown crystals were studied using optical and scanning electron microscopy (SEM, Model JEOL 840). An energy dispersive spectrometer (OXFORD ISIS-300 system) attached to the SEM was used to analyze the stoichiometry of the grown crystals. The carbon and hydrogen content of the grown crystals were determined using a Vario EL III CHNS analyzer. The powder X-ray diffraction pattern was recorded using a Bruker AXS D8 advanced powder diffractometer with Cu Kα radiation (α = 1.5406 Å) at a scanning rate of 2° min⁻¹ with 2θ in the range 10°–50°. The single crystal X-ray diffraction was carried out using a single crystal Oxford X-ray diffractometer. The data so obtained was analyzed with SHEL X. To assess the crystalline perfection of the grown crystals, a PANalytical X’Pert PRO MRD HRXRD using Cu Kα radiation and developed at National Physical Laboratory, New Delhi was used. The rocking curve of the crystal for the (110) diffraction planes was recorded in symmetrical Bragg geometry using the (110) natural faces by performing an ω scan, keeping detector of 2 theta fixed during ω scan. The highly monochromatic X-ray beam (Cu Kα₁) incident on the specimen was obtained using a four-bounce Ge(220) monochromator. The diffracted beam from the specimen was detected using a scintillation detector with a triple-axis three-bounce Ge(220) analyser. A Varian Cary 5000 spectrophotometer was used for the optical characterization in the wavelength range of 25–2485 nm from which the absorption measurements were carried out. Crystals of thickness 1.33 mm were used for the said study. Single crystals of the same thickness were used for the photoluminescence spectroscopy emission spectra using a Perkin Elmer LS-55 luminescence spectrometer in the wavelength range of 400–560 nm at room temperature. The area of the crystal surface exposed to the incident beam was kept constant. A cut-off filter of 390 nm was used to separate out the excitation wavelength from the emission spectra reaching the photomultiplier tube (detector). Refractive index studies were carried out using Brewster’s angle method. The crystals of 1.33 mm thickness were used for these studies using an Abbe refractometer 2WA. Birefringence was conducted by using an Exicor – DUV refractometer. In order to ensure good ohmic contact between the opposite (110) faces of a single crystal for investigation into the dielectric behaviour, the crystal was coated with high grade silver paste, ensuring that the paste did not spread along the sides of the crystal. The capacitance and the dissipation factor of the parallel plate capacitor formed between a pair of electrodes having the sample of PMH as a dielectric medium was measured. The measurements were recorded with the help of a precision LCR meter model Agilient-4284A and further automated by using a computer for the data recording, storage and analysis. Room temperature dielectric behavior of the sample was recorded on application of an ac field (in the frequency range 20 Hz to 1 MHz) using an Agilent 4285A precision LCR meter.

3. Results and discussion

3.1. Single crystal growth and stoichiometric analysis

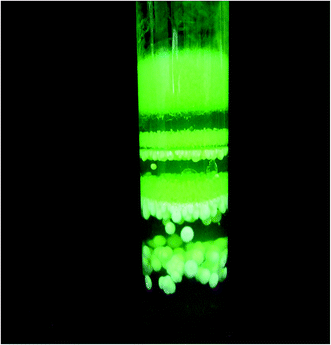
The optimum conditions, determined from a series of experiments, leading to single crystals are established to be gel conc. 0.5 M, LR conc. 0.5 M, UR conc. 0.25, gel age 140 hours, gel pH 6 and a temperature in the range of 35–40 °C; the maximum size of crystals under these optimum conditions being 17 mm × 2.5 mm × 1.5 mm. The mode of growth is dendritic under all the conditions of growth. The tips of these dendrites develop into good quality single crystals of good morphology as they grow deeper into the gel, as shown in Fig. 1. A UR concentration greater than 0.75 M and LR concentration above 0.5 M leads to spherulitic crystal growth. Liesegang ring formation takes place at higher concentrations, >0.75 M of UR, as shown in Fig. 2. In fact, the spherulitic growth seems to become predominant if one moves deeper into the gel column. The Liesegang rings nearer to the gel reactant interface are a combination of crystals with spherulitic morphology along with small single crystals. The crystals of PMH grown under optimum conditions are quite transparent with developed natural faces, as shown in Fig. 3. Fig. 4 is a scanning electron micrograph of a single crystal of PMH illustrating the smooth and flat (110) habit faces of the crystal. The morphological development of the grown crystal is shown in a schematic diagram in Fig. 5.

Fig. 1 Single crystals of PMH developing from the tips of the dendritic formation in the gel.

Fig. 2 Liesegang ring formation in the crystallizer with UR conc. > 0.75 M.

Fig. 3 Single crystals of PMH grown under optimum conditions of growth.

Fig. 4 SEM of PMH as grown under the optimum conditions of growth revealing its morphology.

Fig. 5 Schematic diagram illustrating the morphology of the grown crystal with prominent (110) habit faces.

The experimental and theoretical results of the EDAX and CH analysis are compiled in Table 1(a) and (b), respectively. They suggest the stoichiometric composition to be [Pr₂(C₃H₂O₄)₃(H₂O)₆].

Table 1 (a) EDAX analysis of [Pr₂(C₃H₂O₄)₃(H₂O)₆] single crystals. (b) CH analysis of [Pr₂(C₃H₂O₄)₃(H₂O)₆] single crystals

Element	Experimental (%)	Theoretical (%)
(a)
Pr	39.844	40.489
Oxygen	42.093	41.375
(b)
Carbon	15.384	15.530
Hydrogen	2.643	2.606

---

3.2. X-ray diffraction

The powder X-ray diffraction pattern of PMH is shown in Fig. 6. The diffraction pattern depicts the crystallinity of the grown crystal. CRYSFER and powder-X software were used for analysing the data. The single crystal XRD of the crystal was also recorded. The grown crystals belong to a monoclinic system with space group P2/m. Taking the (hkl) parameters as obtained from the powder XRD, the crystal may be said to fall into a unit pyramid sub-system, which is also analogous with the sub-system of the unit prism of the monoclinic prism system. The lattice parameters for the crystal turn out to be: a = 15.107 Å, b = 11.976 Å and c = 10.343 Å; α = γ = 90° and β = 121.508°. The volume of the unit cell is V = 1871.2704 ų. The cell parameters worked out here turn out to be different from those reported in the literature^5–7 which is because of the absolute difference in the internal bonding of the compound, as confirmed from the crystallographic data obtained from the single crystal XRD. The interplanar spacing (d) values were calculated with the help of lattice parameters which are in good agreement with the experimental (d) values. Various parameters like the (hkl), interplanar spacing (d in Å), full width half maxima of the diffraction peaks (FWHM) and crystallite size (L in Å), micro strain (ε), dislocation density ρ (ρ in 10¹⁵ m m⁻³) and distortion parameter (g) were calculated, using the following well known equations, and are recorded in Table 2(a) and (b). L = K/β cos θ; d = λ/2 sin θ; ε = β cos θ/4; ρ = 1/L² and g = β/tan θ, where λ = 1.54 Å is the wavelength of the Cu Kα X-ray radiation used, β is the full width half maxima (FWHM) of the diffraction peaks, θ is the Braggs angle (degrees) and K is Scherer’s constant (usually taken as 0.89).

Fig. 6 Powder X-ray diffraction pattern of PMH showing the (110) peak as the dominant one.

Table 2 (a) Evaluated parameters from the powder XRD of PMH crystals. (b) Crystallite size (L), micro strain (ε), dislocation density (ρ), and distortion parameter (g) calculated from the 2θ values of powder XRD crystals

(a)
hkl	2 Theta	d (exp) Å	d (cal) Å	Intensity	FWHM
−110	10.710	6.25407	5.953	140.0	0.1219
110	13.029	1.08940	0.0003	1397.3	0.0568
−210	14.331	5.10045	4.445	254.6	0.0614
111	16.534	4.35739	3.875	105.4	0.1066
−102	17.495	4.06495	3.649	82.5	0.1161
021	18.314	4.84025	3.485	136.0	0.0762
−212	18.891	4.69384	3.378	100.3	0.0641
400	27.893	3.19610	2.298	77.4	0.1447
122	28.797	3.09774	2.232	85.0	0.0716
−504	37.204	2.01079	1.736	72.1	0.0850
−541	43.203	2.09205	1.501	67.4	0.0550
−534	43.792	2.06056	1.482	69.4	0.0952

---

(b)
2θ	L (Å)	ε	ρ (10^15 m m^−3)	g
10.710	7.3269	0.0304	18.6	1.446
13.029	15.7244	0.0142	4.0	0.553
14.331	14.5902	0.0153	4.6	0.544
16.534	8.4200	0.0264	14.1	3.394
17.495	7.7391	0.0287	16.7	0.852
18.314	11.8037	0.0188	7.2	0.525
18.891	14.0378	0.0158	5.0	0.429
27.893	6.2986	0.0353	25.2	0.651
28.797	12.7507	0.0175	6.1	0.311
37.204	10.9336	0.0204	8.3	0.284
43.203	17.1814	0.0129	3.4	0.156
43.792	9.9330	0.0224	10.0	0.265

---

Single crystal X-ray diffraction studies were carried out on a single crystal of dimensions 0.35 × 0.30 × 0.25 mm³. Data was collected at 296(2) K using graphite monochromatic Mo Kα radiation using an oscillation method. The data was interpreted and refined by SHEL X to work out the internal structural details. Based on this data, the molecular configuration and molecular packing were worked out. Fig. 7(a) and (b) show the ORTEP diagrams and Fig. 8 depicts the packing diagram of the molecule when viewed along the c-crystallographic direction. An interesting feature of this compound is that two Pr ions are co-ordinated with three ligands and six molecules of water. The bonding behavior of the two Pr ions in the complex is so symmetrical that in the CIF file of the compound it is unable to distinguish one Pr ion with respect to the second one; that is why, in the ORTEP diagram of the compound, Pr is symbolized as Pr₁ at both places. This is also one of the distinguishable factors and has a significant impact on the bonding of the compound, which in other words modifies all the structure sensitive properties of the material accordingly and differentiates this compound from the one reported in the literature.^5–7 The symmetry in the compound leads it towards a sharp melting point.

Fig. 7 (a) ORTEP diagram of the [Pr₂(C₃H₂O₄)₃(H₂O)₆] single crystal. (b) ORTEP diagram of the [Pr₂(C₃H₂O₄)₃(H₂O)₆] single crystal (full structure).

Fig. 8 Packing diagram of the [Pr₂(C₃H₂O₄)₃(H₂O)₆] single crystal.

The crystallographic analysis of [Pr₂(C₃H₂O₄)₃(H₂O)₆] shows that structure consists of a three-dimensional metal–organic framework. The Pr is coordinated to six oxygen atoms of four carboxylate groups from different malonate anions. The Pr is additionally coordinated to three oxygen atoms of water molecules generating a nine-coordinated tricapped trigonal prism constituted by OW(5), OW(6), OW(8), O(1), O(3), O(4), O(7) and O(9). There are two crystallographically independent dicarboxalate malonate anions in the compound [Mal. (1) and Mal. (2)] corresponding to the O(3)O(4)C(3) and O(1)O(2)C(1)C(5), O(8)O(9)C(5) set of atoms, respectively, as shown in Scheme 1.

Scheme 1 Co-ordination modes of Mal. 2⁻ in [Pr₂(C₃H₂O₄)₃(H₂O)₆].

Mal. (1) adopts the μ₄-κ²OO′; κO′; κ²O′′O′′′;κO′′′ coordination mode, bidentate through O(3) and O(4) toward the Pr and monodentate across O(3) towards another Pr, and the atoms symmetry related. Mal. (2) acts in a bidentate manner through O(1) and O(9) towards the Pr and in a bridging monodentate fashion through O(8) μ₂-κO;κO′;κO′′. The molecule adopts extended 3-D framework when viewed along c-crystallographic orientation. The compound is packed in such a fashion that the Pr ions act as nodes alternatively while different malonate anions bridge the adjacent Pr ions. One bridging carboxylate group O(4)C(3)O(3) of the malonate anion crosslinks the linear chains, as indicated in the respective ORTEP and packing diagrams. The distance between the two Pr metal ions is 11.615(8) Å, which is different from the reported values.^5–7 The bond length between the Pr and the oxygen of a water molecule is 2.57 Å. Each Pr ion is coordinated with three water molecules and these water molecules stabilize the extensive three dimensional frameworks through a large amount of hydrogen bonding. The molecule has both intra and intermolecular hydrogen bonds of the type O–H⋯O. In all the hydrogen bonds, O(3)O(4)O(5) and O(6) of the water molecules act as both donors and accepters whereas the carboxylate oxygens O(3)O(4)O(1)O(9)O(2)… act as acceptors.

For the sake of clarity, comparison of the single crystal XRD data pertaining to this compound as reported in the literature^5–7 and the present paper are similar in terms of the stoichiometric composition, the extensive framework of hydrogen bonds which stabilizes the entire structure and the co-ordination number. However, it differs from the reported ones in terms of space group, cell parameters, cell volume, reliability index factor R, internal molecular features like metal ion distances and the symmetrical bonding nature of the metal ion with the ligands.

3.3. High-resolution X-ray diffraction

Fig. 9 shows the HRXRD rocking curve for the (110) diffraction plane of PMH. One finds a single and sharp peak with a FWHM of 19 arcsec, which is indicative of a good crystal quality free from structural grain boundaries. However, it is interesting to note that there is asymmetry in the rocking curve. As we can see for a fixed angular deviation (θ) of the glancing angle with respect to the peak position, the scattering intensity is maximum in the positive direction in comparison to that of the negative direction, indicating that the crystal contains more interstitial type defects than vacancy defects. Due to interstitial defects (impurities or self-interstitials at interstitial sites), the lattice around these defects undergoes compressive stress⁸ resulting in a decrease in the interplanar spacing (d). As a consequence of this, it leads to a greater scattering intensity which is sometimes also known as diffuse X-ray scattering at slightly higher Bragg angles (θ_B) (d and sin θ_B being inversely proportional to each other in the well-known Bragg’s equation). The reverse is true if it were a vacancy defect.⁹ It is worth noting that there are no multiple peaks in the rocking curve which suggests that the density of interstitial defects is low and so does not affect the long range order of the crystal.¹⁰

Fig. 9 HRXRD of the (110) plane of the PMH single crystal.

3.4. Optical characteristics

Fig. 10 is a UV-Vis-NIR spectrum recorded from the crystal. It shows absorption peaks at 272, 443, 475, 595, 1020, 1442, 1552, 1609, 1994 and 2482 nm. In order to determine the nature of the transitions and the value of the optical band gap, the optical absorption coefficient α was calculated using the relation: α = 2.303 × A/t, where t is the thickness (1.33 mm) of the single crystal. According to the Tauc relation,¹¹ the absorption coefficient (α) for a material is given by the relation: (αhν) = A(hν − E_g)^p, where E_g is the optical band gap, h is Planck’s constant, ν is the frequency of incident photons and ‘p’ is the index that characterizes the optical absorption process; p is theoretically equal to 2, 3, 1/2 and 3/2 corresponding to indirect allowed, indirect forbidden, direct allowed and direct forbidden transitions respectively.^12,13 The plot of (αhν)^3/2 versus hν is shown in Fig. 11. The band gap was estimated by taking hν in the high absorption range followed by extrapolation of the linear portion to zero abscissa to give the band gap.¹⁴ The direct forbidden energy band gap estimated to be 5.4 eV is found to be the prominent transition that takes place in the material and the value so obtained is in close proximity of other tartrate and malonate based single crystals.¹⁵

Fig. 10 UV-Vis-NIR spectrum of the PMH single crystals.

Fig. 11 Tauc plot for the calculation of the optical band gap of the PMH single crystals.

It is clear from the spectrum that there are a number of absorption peaks with different areas of cross section throughout the entire spectrum. The absorption peak at 272 nm corresponds to C=O, in which the n → π* transition occurs. The absorption peaks at 443, 475 and 595 nm are very sharp with decimal absorption coefficients and are due to forbidden f → f transitions which may appear because of the point defects (interstitial sites); normally defects in the crystal structure generally act as photon trapping centers and absorb light radiation, which leads to poor transparency (absorbance), and the same is clear from the rocking curve of the HRXRD shown in Fig. 9. From 625–960 nm there is a wide transmittance window (reduced absorbance), which is a good sign for PMH in connection with its use in the multi-electronic industry.^16,17 Absorption bands occurring at 1020, 1442, 1552, 1609, 1994 and 2482 nm are highly diffuse and are due to the vibrational modes of the molecule. It is worth mentioning here that the ordinate axis of Fig. 10 shows the lower absorption coefficient. This reflects that they are highly transparent in nature, as the energy is absorbed by the ligand and the same is transmitted by the metal. This property enhances the applications of lanthanides (Pr³⁺) co-ordinated with organic ligands (malonic acid) which are used as fluorescent materials in industry.

Rare earth materials are not good absorbers due to forbidden 4f–4f inner transitions. However, by ‘antenna effect’, as proposed by Lehn, these materials, when co-ordinated with organic ligands, could be seen as light conversion molecular devices.

Fig. 12 shows the photoluminescence (PL) emission of PMH. It follows the down-conversion process because, in Ln containing materials, the 4f transitions are strictly forbidden due to parity reasons. In case of Pr³⁺, there are as many as 327 levels of 4f configurations. These levels further increase in number due to crystal field splitting and, when these rare earth ions are coordinated with a ligand, more and more splitting takes place. As such they are not directly good absorbers. However, such a behaviour can be developed by co-ordinating rare earth ions (Pr³⁺) with organic ligands (malonic acid). Generally, down-conversion is a phenomenon whereby one or more photons of higher energy are absorbed by a material and re-emitted as a lower energy photon. Materials able to cause this effect are known as down-converters. In the present PL experiment, the material has been tuned (excited) over a wide range of wavelengths, from 200 to 850 nm, so as to get a good absorption peak. A wavelength of 272 nm was found to be feasible for excitation and a corresponding intense peak was found at 445 nm. The crystal shows strong blue emission. Point defects which are present generally act as photon trapping centers¹⁸ and absorb light radiation, which is responsible for the blue emission by the material. The HRXRD results support the presence of point defects.¹⁹ Since in organic ligands, organic chromophores are better absorbers than Ln ions, ligand to metal energy transfer is most probable due to an antenna effect which helps to increase the luminescence efficiency of Pr³⁺ ions.

Fig. 12 Photoluminescence emission spectra of PMH single crystals.

The refractive index studies were conducted using Brewster’s angle method on single crystal of 1.33 mm thickness. The crystal was mounted on a rotating mount at an angle varying from 0 to 90 degrees. Following the principle of polarization, the crystal was rotated until the reflection of the laser beam disappeared. This angle was noted and the Brewster’s angle (θ_p) was measured to be 57.3°. The refractive index was calculated using the relation μ = tan θ_p, which turns out to be 1.56.

Birefringence measurements were also undertaken on PMH single crystals of 1.33 mm thickness. The light from He–Ne laser source was allowed to pass through the optical plane of the crystal when placed in between the polarizer and the analyzer. The transmitted light from the analyzer, which undergoes interference, forms the fringe pattern which appears on the screen. The crystal was rotated to capture the interference pattern which appeared to be distorted. The distorted nature in the fringes could be due to various types of defects present in the crystal, like strain during growth, point defects, color centers or any other.²⁰ The HRXRD studies show that the crystals do contain point defects. Due to the presence of defects, the intensity of the emergent light from the crystal was diminished. To calculate the birefringence (Δμ), the following relation was used²¹

Δμ = λ/πt sin⁻¹(I/I₀)^1/2

where I and I₀ are the intensity of light before and after passing through the crystal and t is the crystal thickness. The position of the sample was continuously varied until a maximum in the intensity of light came out. The value of Δμ was determined to be 0.01593, which is in good agreement with other semi-organic crystals.^21,22 This study helps us to locate exactly the optical axis and the growth orientation along the same axis of the grown crystal.

3.5. Dielectric behaviour

A single crystal with prominent (110) faces was mounted between a pair of electrodes. The dielectric constant ε_r was computed using the relation:

ε_r = 4Ct/0.0885A

where C represents the capacitance of the crystal, t the thickness and A the area of the crystal. Single crystals with a very low dielectric constant value are required by industries dealing with microelectronic technology.²³ L-Arginine oxalate and L-arginine acetate are also reported to be low value dielectric materials.²³ It is worth mentioning that the dielectric characteristics reported here for the PMH single crystal identifies it as a promising material with potential application in microelectronics. The dependence of the dielectric constant (ε_r) and dielectric loss (tan δ) on the frequency of the applied ac field in the case of PMH was studied within the frequency range of 20 Hz to 1 MHz. The dielectric characteristics are supported by the optical properties and HXRD results of the crystal. The variation of ε_r with frequency is shown in Fig. 13. It is clear that there is a resonance peak at a very low frequency and the dielectric constant of the material is quite high in this region. The dielectric constant starts to decrease with a further increase in the frequency of the applied ac field. Such behaviour is a normal trend of dielectric materials. The gradual decrease in the dielectric constant with frequency suggests that the material under consideration has ferroelectric domains of different sizes and hence varying relaxation times.²⁴ In the low frequency range, all types of polarisation mechanisms (electronic, ionic, dipolar and space charge) may be active.^25–27 As the frequency increases, a point will be reached where the space charge cannot be sustained and comply with the external field.²⁸ Space charge polarisation is responsible for a high value of the dielectric constant at lower frequencies, which indicates a lower number of defects in the crystal. Such a situation is more important for optical applications.²⁹ This observation supports the crystalline perfection of the grown crystal, as also revealed from the high resolution XRD rocking curve of the crystal for (110) diffraction planes described earlier.

Fig. 13 Variation of the dielectric constant of [Pr₂(C₃H₂O₄)₃(H₂O)₆] with the frequency of the applied field.

The variation of the dielectric loss (tan δ) with frequency is shown in Fig. 14. The figure reveals that the dielectric loss is high at lower frequency and decreases with increases in frequency. At higher frequencies, all the polarisation mechanisms are not operative and the energy need not be spent on rotating the dipoles. As a result, the dielectric loss is also minimum. The characteristic of a low dielectric loss with a high frequency for the sample suggests that the crystal possesses enhanced optical qualities with fewer defects and this parameter plays a vital role for the construction of devices from nonlinear optical materials.^30,31

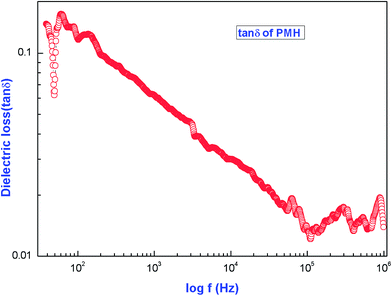Fig. 14 Dependence of dielectric loss on the frequency of the applied ac field for [Pr₂(C₃H₂O₄)₃(H₂O)₆].

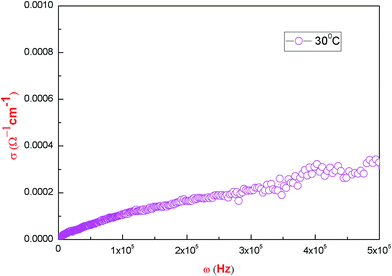
The ac conductivity ln σ_ac is calculated by substituting the value of capacitance (given directly by the instrument) into the formula σ_ac = 2πfε₀ε_r tan δ; where ε₀ stands for the absolute permittivity in free space having a value of 8.854 × 10⁻¹² F m⁻¹ and f is the frequency in hertz. Fig. 15 shows the variation of conductivity with frequency. In order to study the nature of the conductivity as a function of frequency, Jonscher’s power law, as given below, has been used:^32,33

σ(ω) = σ₀ + Aω^s

where ω is angular frequency, σ₀ is frequency independent factor (DC conductivity) and s is a power exponent which is a function of temperature and can be calculated by plotting log σ versus log ω. The value of s lies within the limits 0 ≤ s ≤ 1.³⁴ When s = 0, the electric conduction is frequency independent (dc conduction) which refers to conductivity at very low frequency. When s > 0, the conduction is frequency dependent which means ac conduction.³⁶ In the present study, s was calculated from the plot of log σ versus log ω, as shown in Fig. 16, at ambient temperature, which comes out to be s = 0.011. This value of ‘s’ suggests that the electrical conductivity for this crystal is determined by the hopping conduction of proton transport within the framework of hydrogen bonds due to presence of water molecules. Detailed thermo-analytical studies of the material have been conducted, which confirm the presence of six water molecules in the present material and the details of the same will be communicated elsewhere. In the present case, the conductivity increases smoothly with increases in frequency. As such there is no sharp increase that would be the characteristic of a superprotonic phase transition.²⁵ The pycnometric density and X-ray density of the title compound do not differ, which goes in support of our observation that there exists some fraction of point defects in the crystal. This is in support of the variation of conductivity of the type reported here.³⁵ Here, we can conclude that the increase in conductivity in PMH is due to the presence of hydrogen bonds. It is reported²⁴ that the conduction in tartrates and malonates is due to the rotation of tartrate/malonate ions. There is a finite probability that when the temperature of the tartrate/malonate crystal approaches 300 K, the bonds of the hydrogen gets weakened due to the rotation of tartrate/malonate ions and they give rise to L and D-defects. This results in an enhanced conduction in these materials.²⁴ Another possibility is the presence of point defects, which also play an essential role in the conduction process. The optical and HRXRD results confirm the same.

Fig. 15 Dependence of the conductivity of [Pr₂(C₃H₂O₄)₃(H₂O)₆] on the frequency of the ac field.

Fig. 16 Curve of log σ versus log ω.

4. Conclusion

The gel technique of crystal growth yields single crystals of PMH with prominent (110) habit faces; the stoichiometric composition is established to be [Pr₂(C₃H₂O₄)₃(H₂O)₆]. The optimum conditions of growth are gel conc. 0.5 M, LR conc. 0.5 M3, UR conc. 0.25, gel age 140 hours, gel pH 6 and a temperature in the range of 35–40 °C. HRXRD suggests that the crystals grown under the optimum conditions are of good quality. The crystal falls under the monoclinic system with the lattice having a space group of P2/m and cell parameters of a = 15.107 Å, b = 11.976 Å and c = 10.343 Å; α = γ = 90° and β = 121.508° and V = 1871.2704 ų. Based on the single crystal XRD results, the molecular arrangement within the internal structure is determined. The crystallographic data presented here differentiates it from the one reported in the literature, with respect to the reliability factor, space group, cell parameters and the molecular arrangement. The UV-Vis-NIR spectrum indicates optical absorption peaks at 272, 443, 475, 595, 1120, 1442, 1552, 1609, 1954, and 2482 nm in wavelength. The forbidden energy band gap is estimated at 5.4 eV. Photoluminescence study leads to a down-conversion process taking place in the compound. Refractive index measurements of the crystal lead to a value 1.55. The birefringence Δμ of the crystal is calculated to be 0.01593. A crystal of PMH is shown to have a low dielectric constant and can thus be a promising material for the microelectronic device applications.

Acknowledgements

The author (Nazir Ahmad) is highly thankful to Prof. Rajat Gupta, the Director, NIT Srinagar and Prof. Fayaz Ahmad Mir, Registrar NIT Srinagar, for taking a keen interest and extending the financial support for carrying out this research work. The author is thankful to Dr K. K. Maurya, Scientist at NPL, New Delhi for the HRXRD facilities and Prof. H. N. Sheikh, Department of Chemistry, University of Jammu, for useful discussions. The author is also thankful to Mr P. L. Saproo of NIT, Srinagar for his generous help and understanding.

References

1. K. Matsumoto and H. Kuroya, Bull. Chem. Soc. Jpn., 1972, 45, 1755.
2. N. J. Ray and B. J. Hathaway, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1982, 38, 770.
3. R. Hamalainen and A. Pajumen, Suom. Kemistil. B, 1973, 46, 285.
4. A. Karipides, J. Ault and A. Thomas Reed, Inorg. Chem., 1997, 16, 3299.
5. B. H. Doreswamy, M. Mahendra, M. A. Sridhar, J. S. Prasad, P. A. Varughese, K. V. Saban and G. Varghese, J. Mol. Struct., 2003, 659, 81–88.
6. M. H. Molina, P. A. L. Luis, T. Lopez, C. R. Perez, F. Lloret and M. Julve, CrystEngComm, 2000, 31, 1–5.
7. E. Konstantina Chrysomallidou, P. Spyros Perlepes, A. Terzis and C. P. Raptopoulou, Polyhedron, 2010, 29, 3118–3124.
8. G. Bhagavannarayana, S. Parthiban and S. Meenakshisundaram, Cryst. Growth Des., 2008, 8, 446–451.
9. S. K. Kushwaha, K. K. Maurya, N. Vijayan and G. Bhagavannarayana, CrystEngComm, 2011, 13, 4866–4872.
10. G. Bhagavannarayana, S. K. Kushwaha, M. Shakir and K. K. Maurya, J. Appl. Crystallogr., 2011, 44, 122–128.
11. J. Tauc, Amorphous and Liquid Semiconductors, Plenum, NewYork, 1974, pp. 159–220.
12. V. Krishnakumar, D. K. Awasti, F. Singh, P. K. Kulriya and R. Nagalaskshmi, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 256, 675.
13. S. K. Arora, V. Patel, B. Chudasama and B. Amin, J. Cryst. Growth, 2005, 275, 657.
14. R. P. Khatri, S. M. Vyas, P. J. Patel, D. Shah and M. P. jani, Asian J. Chem., 2000, 21, 135.
15. P. P. Kumar, V. Manivannan, P. Sagayaraj and J. Madhavan, Bull. Mater. Sci., 2009, 32, 431.
16. P. N. S. Kumaria and S. Kalainathan, characterisation of lead(II) Chloride single crystals grown in silica gel, Cryst. Res. Technol., 2008, 43, 413–416.
17. D. Kalaisevi, R. M. Kumar and R. Jayavel, Single crystal growth and properties of semiorganic nonlinear optical L-arginine hydrochloride monohydrate crystals, Cryst. Res. Technol., 2008, 43, 851–856.
18. H. Xu, D. Lee, S. B. Sinnott, V. Gopalan, V. Dierolf and S. R. Phillpot, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 144104.
19. S. J. Xu, G. Li, S. J. Chua, X. C. Wang and W. Wang, Appl. Phys. Lett., 1998, 72, 2451–2453.
20. V. Vasudevan, R. R. Babu, A. R. Nelcy, G. Bhagavannarayana and K. Ramamurthi, Bull. Mater. Sci., 2011, 34, 469–475.
21. A. M. Nasr, International Journal of Material Science, 2007, 2, 103.
22. Y. Zhang, H. Li, B. Xi, Y. Che and J. Zheng, Mater. Chem. Phys., 2008, 108, 192.
23. M. Meena and C. K. Mahadevan, Mater. Lett., 2008, 62, 3742–3744.
24. N. Ahmad, M. M. Ahmad and P. N. Kotru, J. Cryst. Growth, 2014, 412, 72–79.
25. M. Meena and C. K. Mahadevan, Cryst. Res. Technol., 2008, 43, 166–172.
26. S. M. DharmaPrakash and P. M. Rao, J. Mater. Sci. Lett., 1989, 8, 1167.
27. N. Vijayan, G. Bhagavannarayana, G. C. Budakoti, B. Kumar, V. Upadhyaya and S. Das, Mater. Lett., 2008, 62, 1252.
28. S. Kuryan, R. Abraham and J. Isac, Indian J. Pure Appl. Phys., 2008, 46, 30.
29. A. C. Peter, M. Vimalan, P. Sagayaraj and J. Madhavan, Arch. Appl. Sci. Res., 2010, 2, 191.
30. S. A. Martin Britto Dhas and S. Natarajan, Opt. Commun., 2008, 281, 457.
31. D. Kalaiselvi, R. M. Kumar and R. Jayavel, Cryst. Res. Technol., 2008, 43, 851.
32. A. K. Jonscher, The universal dielectric response, Nature, 1977, 267, 673–679.
33. A. K. Jonscher, A new understanding of the dielectric relaxation of solids, J. Mater. Sci., 1981, 16, 2060.
34. M. D. Ingram, Ionic conductivity in glass, Phys. Chem. Glasses, 1987, 28, 215–234.
35. C. C. Desai and A. N. Hanchinal, J. Mater. Sci. Lett., 1985, 4, 419–421.
36. W. Kuang and S. O. Nelson, Low-Frequency Dielectric Properties of Biological Tissues: A Review with Some New Insights, Trans. ASAE, 1998, 41, 173–184.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra09502f

---