Molecular dynamics simulation of the diffusion behavior of water in poly(vinylidene fluoride)/silica hybrid membranes

Abstract

A molecular dynamics (MD) simulation is employed to investigate the effects of the concentration and size of silica particles on the diffusion behavior of water in poly(vinylidene fluoride) (PVDF)/SiO₂ hybrid membranes. The membranes with different concentrations of SiO₂ particles (class I) and with different sizes of SiO₂ particles (class II) are designed and studied. The X-ray diffraction patterns and mean-square displacement (MSD) values of PVDF, the fractional free volume (FFV) characteristics and diffusion coefficients of water are discussed. The results revealed that the incorporation of silica particles into PVDF increased the polymer chain mobility and FFV in PVDF/SiO₂ hybrid membranes. The diffusion coefficient of water presented an increase as the concentration of SiO₂ increased (0–14.6 wt%). With the same concentration of SiO₂, when the sizes of the SiO₂ particles are different, the diffusion coefficient of water presented an increase first and then decreased as the size of the silica increased (radius: 0.794–1.26 nm). When the radius of the silica is nearly 1 nm, the diffusion coefficient of water in the membranes is at its largest (4.50 × 10⁻¹² m² s⁻¹).

---

1 Introduction

Organic–inorganic hybrid membranes are fabricated by blending inorganic particles with organic polymer membranes. They have many interesting properties which are not found in pure polymer membranes,^1–4 such as transport properties, as well as chemical and thermal stability. They can be widely used in the fields of automobiles, aeroplanes, electronics, architecture, new process and highly effective catalysts, environment-protecting materials, and so on. Their versatility is mainly due to the presence of inorganic filler materials, which can alter the mechanical properties of the polymer material significantly.^5–7 Organic–inorganic hybrid membranes have attracted intense interest as potentially “the next generation” of membrane materials.⁸ Thus, it is necessary to understand the relations between the structural characteristics of hybrid membranes and their properties. Much effort has been devoted to experimental investigations. However, little has been reported about the theoretical analysis of the morphology upon the transport properties of small molecules in the hybrid membranes. One possible reason is that it is difficult to obtain accurate information using experimental technologies because of the restriction of the limited volume of the interfacial region.⁸

It has been validated that molecular dynamics (MD) simulations are able to reveal the microstructure of hybrid membranes and provide the dynamics of the permeating compounds at the molecular level. It is possible that the diffusion behavior of small molecules is estimated in the interfacial region at the molecular level via MD simulation techniques. Some researchers have investigated the effects of inorganic particles on the interfacial morphology and the subsequent influence on diffusion properties. Tamai^9–11 studied the diffusion process of methane, water, and ethanol in PDMS and polyethylene using MD simulations. Matthias Heuchel et al.¹² analyzed the diffusion behaviors of oxygen, nitrogen, methane, and carbon dioxide through polyimide membranes using molecular simulations. Sakintuna et al.¹³ measured the diffusion coefficients and modes of transport of methanol, ethanol, n-propanol, 2-propanol and n-butanol through a zeolite. However, there is little literature devoted to the investigation of the diffusion behavior of water in PVDF/SiO₂ hybrid membranes.

PVDF is one of the most extensively applied membrane materials in industry, because of its outstanding antioxidation properties, superior thermal and hydrolytic stabilities, as well as good mechanical and membrane forming properties. However, its hydrophobic nature that often results in severe membrane fouling and decline of permeability, has been a barrier for its application in water treatment.¹⁴ Inorganic materials that could be blended with PVDF include titanium dioxide (TiO₂),¹⁵ zirconium dioxide (ZrO₂),¹⁶ alumina (Al₂O₃)¹⁷ and some small molecule inorganic salts, such as lithium salts.¹⁸ Among the numerous inorganic materials, silica (SiO₂) is the most convenient and widely used because of its mild reactivity and well-known chemical properties.¹⁹ Compared with the pure PVDF membrane, PVDF/SiO₂ hybrid membranes have many outstanding properties, such as high-porosity and high intensity.

In this work, the effects of inorganic SiO₂ particles on the diffusion properties of small penetrant molecules in PVDF/SiO₂ hybrid membranes are investigated using MD simulations. It should be mentioned that silica particles have an α-quartz crystal structure, which is impermeable for the penetrant in order to exclude the influence of connected channels within the inorganic particles. The X-ray diffraction patterns, chain mobility, free volume characteristics and the diffusion coefficient of water in the PVDF control membrane and hybrid membranes were studied using MD simulations.

2 Simulation details

Molecular dynamics (MD) simulations were performed using the Materials Studio (version: 4.2) package, which was developed by Accelrys Software Inc. Energy minimization was conducted using the smart minimizer method which switched from steepest-descent to conjugated gradient and then to the Newton method as the energy derivatives decrease in order to accelerate the computation. The Andersen²³ and Berendsen²⁴ methods were employed to control temperature and pressure, respectively. A non-bond cutoff distance of 9.5 Å was employed to evaluate the non-bond interaction. The spline width and buffer width for the cutoff distance were 1.0 Å and 0.5 Å, respectively. The time step was set as 1.0 fs for all dynamics runs.

The COMPASS^20–22 (condensed phase optimization molecular potentials for atomistic simulation studies) module was applied in this work. The COMPASS force field is the first ab initio force field that has been parameterized and validated using condensed-phase properties in addition to various ab initio and empirical data for the molecules in isolation. The electrostatic potential energy was calculated using the Ewald²⁵ summation technique and the van der Waals potential energy was calculated using the atom based²⁶ technique.

The PVDF polymer chain consists of 100 repeat units. The silica particle with an approximate radius of 0.794 nm was constructed using the α-quartz silica crystal structure imported from the MS package, which was named as SiO₂-1 (Fig. 1a). Two atactic PVDF chains and a number of silica particles were embedded into the cubic cells by using the Amorphous Cells Construction tools, which are filled with 5 water molecules with approximate 1.77 g cm⁻³ density to form all kinds of initial polymer membranes. An initial energy minimization was carried out at the initial stage to eliminate the bad contact. Cell samples were designated as PVDF, PVDF1SiO₂-1, PVDF2SiO₂-1, and PVDF4SiO₂-1 (Fig. 1d–g) respectively according to the number of silica particles in the PVDF unit, marked as class I. In class I, PVDF, PVDF1SiO₂-1, PVDF2SiO₂-1, and PVDF4SiO₂-1 correspond to the different concentrations of 0, 3.7, 7.3 and 14.6 wt%, respectively. In order to research the effect of the size of SiO₂, another two silica particles, SiO₂-2 and SiO₂-4 (Fig. 1b and c), were constructed respectively. SiO₂-2 is twice the volume of SiO₂-1, and SiO₂-4 is four times the volume of SiO₂-1. The three particles possess a radius of 0.794, 1.00 and 1.26 nm respectively. Then another kind of model marked as class II is designed, which includes PVDF, PVDF4SiO₂-1, PVDF2SiO₂-2, and PVDF1SiO₂-4 (Fig. 1d, g–i). In class II, except PVDF, the other three models possess the same concentration of 14.6 wt% and different size of SiO₂ particles.

Fig. 1 (a) Structure of SiO₂-1. (b) Structure of SiO₂-2. The volume of SiO₂-2 is twice that of SiO₂-1. (c) Structure of SiO₂-4. The volume of SiO₂-4 is four times that of SiO₂-1. (d) The membrane of PVDF. (e) The hybrid membrane of PVDF1SiO₂-1. (f) The hybrid membrane of PVDF2SiO₂-1. (g) The hybrid membrane of PVDF4SiO₂-1. (h) The hybrid membrane of PVDF2SiO₂-2. (i) The hybrid membrane of PVDF1SiO₂-4.

At the beginning of the simulation, the discover minimizer was rerun several times to get a more stabilized configuration, the energy vs. iteration curves are shown in Fig. 2. Then a 200 ps NPT²⁸ (T = 298 K, P = 1.01 × 10⁵ Pa) equilibration was adopted to obtain the justified density, followed by 1000 ps NVT²⁷ (T = 298 K) dynamics. The temperature was controlled using the Andersen thermostat method and the pressure was controlled by the Berendsen method. The vdW interactions were calculated by using the atom based method with the cutoff distance set to 9.5 Å, and the coulomb interactions were calculated by using the Ewald method. The trajectories were saved every 1000 steps for further analysis.

Fig. 2 Energy vs. iteration (left: the first run of the discover minimizer; right: the last run of the discover minimizer).

3 Results and discussion

3.1 Class I: different concentrations of SiO₂

In class I, SiO₂-1 was employed to construct models PVDF1SiO₂-1, PVDF2SiO₂-1, and PVDF4SiO₂-1, which correspond to the different concentrations of 0, 3.7, 7.3, 14.6 wt%, respectively. In this part, the influence of different concentrations of silica on interfacial morphology and transport properties were studied.

3.1.1 Simulated X-ray diffraction pattern of the membranes. Simulated X-ray diffraction has been widely used to obtain the interchain distance (d-spacing) of the polymer.^29–32 The discover module was employed to investigate the X-ray diffraction pattern. The interchain distance was calculated from eqn (1):where λ is the wavelength (1.5418 Å for Cu_(Kα) radiation) and θ is the scattering angle corresponding to the maximum of the principle peak in a plot of intensity versus the scattering angle, 2θ.

The simulated diffraction patterns of the hybrid membranes are shown in Fig. 3. It was shown that the PVDF control membrane and PVDF/SiO₂ hybrid membranes generally existed in the amorphous state. It was also noted that the hybrid membranes exhibit a typical peak at about 34.92°, which is quite similar to the PVDF control membrane. It can be found that the peak intensity of the membranes follows the order of PVDF > PVDF1SiO₂-1 > PVDF2SiO₂-1 > PVDF4SiO₂-1 from Fig. 3. This revealed that the intensity of the peak decreases while the mass fraction of SiO₂ increases. It also can be found that the peak intensity of PVDF4SiO₂-1 is apparently weaker than the peak intensity of the other three membranes (PVDF, PVDF1SiO₂-1, PVDF2SiO₂-1). The content of the hybrid membrane of PVDF4SiO₂-1 is four times the nanoparticles of SiO₂-1, and the concentration of SiO₂-1 is 14.6 wt%. First, each of the four silica nanoparticles has a large interaction, which can deduce the apparent peak intensity of the PVDF4SiO₂-1. Secondly, there is an interaction among the four silica nanoparticles, which may be a factor to decrease the peak intensity of PVDF4SiO₂-1. Generally speaking, the PVDF/SiO₂ hybrid membranes possessed less crystalline domains as the silica concentration increased, which is beneficial to the transport of small penetrants. The crystalline regions where the polymer chains are orderly packed are disrupted owing to interaction between the silica particles and polymer chains.

Fig. 3 Simulated X-ray diffraction patterns of the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class I.

3.1.2 Mobility of the PVDF polymer chain. As reported, chain mobility is closely related to the transport properties of the hybrid membranes.³³ The interaction between inorganic particles and polymer chains plays a key role in chain mobility.³⁴ Thus, it is crucial to understanding the effects of incorporated inorganic particles on the mobility of the polymer.

The mobility of the polymer is studied by examining the mean-square displacement (MSD) of the polymer chain.

〈Δr(t)²〉 = 〈(r_i(t) − r_i(0))²〉 (2)

where r_i(t) and r_i(0) are the position of atom i at time t and 0, respectively. The bracket denotes the ensemble average, which is obtained from averaging over all time origins when t = 0.

The MSD of the polymer chain in the PVDF/SiO₂ hybrid membranes is displayed in Fig. 4. The larger the slope of the MSD curve is, the stronger the chain mobility is. From Fig. 4, it is shown that the mobility of the polymer chain in hybrid membranes is stronger than that in the PVDF control membrane. In PVDF4SiO₂-1 hybrid membranes, because of the higher concentration of silica particles and fewer crystalline domains, the polymer chain exhibits stronger mobility.

Fig. 4 MSD (the mean-square displacement) of PVDF in the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class I.

3.1.3 Free volume of the membranes. As we know, there is lots of space in the membrane, which is called the free volume. The size and distribution of the free volume are key issues for the membrane morphology along with its macroscopic separation performances. The free volume characteristics were studied using nanometer molecules as probes using the MD method.

The free volume of the PVDF/SiO₂ and pure PVDF membranes was characterized using a hard spherical probe. The Connolly surface (also called the molecular surface, shown in Fig. 5) is calculated when the probe molecule with the radius R_p rolls over the van der Waals surface, and the free volume is defined as the volume on the side of the Connolly surface without atoms. The FFV is determined by the ratio of the free volume to the total volume of the model. It should be mentioned that the free volume obtained by the probe method excludes the volume which is inaccessible to the probe. The free volume plays a crucial role in the transport behavior of penetrant molecules in membranes. The larger the fractional free volume, the better the free volume connectivity will be, and the faster the diffusion rate of small penetrants will be. The penetrant molecules are modeled by spheres with a radius of 0, 0.5, 1.0, 1.40 and 1.90 Å (collision radius). It should be mentioned that the free volume obtained using the probe method excludes the volume which is inaccessible to the probe.

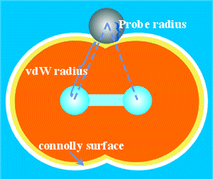Fig. 5 Definition of the Connolly surface. (M. L. Connolly, Science, 1983, 221, 709; M. L. Connolly, J. Appl. Crystal., 1983, 16, 548.)

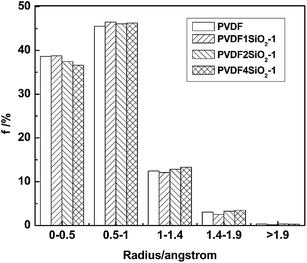
The results of the FFV, which depends on the radius of the probe, are shown in Table 1. The obtained results imply that the FFV drops sharply as the probe size increased. When the radius is 0 Å, the FFV of PVDF/SiO₂ hybrid membranes are larger than that of the pure PVDF membrane and follow the order of PVDF4SiO₂-1 > PVDF2SiO₂-1 > PVDF1SiO₂-1 > PVDF; when the radius is 0.5, 1.0 and 1.4 Å, the FFVs of the PVDF/SiO₂ hybrid membranes are larger than that of the pure PVDF membrane and follow the order of PVDF4SiO₂-1 > PVDF2SiO₂-1 > PVDF1SiO₂-1, but the FFVs of the PVDF/SiO₂ hybrid membranes are not larger than that of the pure PVDF membrane; however, when the radius is 1.9 Å, the changes of the FFV of the PVDF/SiO₂ hybrid membranes don’t show an obvious regulation. The specific reasons for this need be studied further in future work. It can be explained that when the silica particles are embedded in a glassy polymer, a gap appears at the organic–inorganic interface and its width depends greatly on the rigidity of the polymer and particles as well as the interaction between them.³⁵ Thus, there are more free volume voids exhibited in PVDF4SiO₂-1. A large amount of voids in the polymer bulk decreases the interchain interaction of the polymer and therefore enlarges the free volume voids in the polymer.

Table 1 FFV (the fractional free volume) of the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class I

Radius of the probe (Å)	0	0.5	1.0	1.4	1.9
PVDF	24.09	14.79	3.83	0.82	0.08
PVDF1SiO2-1	24.15	14.79	3.57	0.64	0.03
PVDF2SiO2-1	24.26	15.18	4.00	0.88	0.09
PVDF4SiO2-1	24.45	15.49	4.18	0.93	0.07

---

f is defined as the ratio of the FFVs as shown in eqn (3):

where FFV_i, FFV_j, FFV₀ are the FFVs when the probe radius is i, j, and 0 Å, respectively. The ratios of the different radii of the FFVs are shown in Fig. 6. The f_0–0.5 is slightly decreased when the mass fraction of the silica increased, while f_1.0–1.4 is increased. It can be concluded that the size of the free volume voids increased as the mass fraction of silica increased. And it contributes to the larger interchain distance, which is consistent with the observation that PVDF/SiO₂ hybrid membranes possessed fewer crystalline domains with increasing SiO₂ concentration (as studied in 3.1.1). From Fig. 6, it can also be found that there is a significant difference between f_0.5–1 and f_1–1.4. There is a significant effect of the probe radius on the FFV when the radius of the probe is less than 1 Å. When the probe radius is more than 1 Å, the change of FFV is not obvious.

3.1.4 Penetrant diffusion in membranes. The diffusion coefficients (D) of water were analyzed using the Einstein equation:where D is the diffusion coefficient and 〈(r_i(t) − r_i(0))²〉 is the MSD of the penetrants.

In this part, penetrant molecules (five water molecules) were inserted into the models. The diffusion coefficients were an averaged value from all penetrant molecules and were investigated under the NVT (T = 298 K) condition for 2000 ps. The diffusion coefficients of water are listed in Table 2. It was shown that an increase of the diffusion coefficients of water increased the mass fraction of silica particles. The chain mobility and the free volume are two key factors that affect the penetrant diffusivity in the membranes. A higher chain mobility induces a higher frequency of diffusion paths forming and disappearing. Higher FFVs always mean more accessible free volume voids in the membranes for the penetrant diffusion. Therefore, the diffusion coefficient of water in the PVDF4SiO₂-1 membrane is higher than that of the other three membranes.

Table 2 Diffusion coefficients of water in the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class I

Membranes	Diffusion coefficient
PVDF	1.80
PVDF1SiO2-1	2.77
PVDF2SiO2-1	2.67
PVDF4SiO2-1	3.73

---

3.1.5 The relationship between the diffusion coefficient and the other three properties (crystalline domains, mobility of the PVDF chain, and free volume of the membranes). From the figure of the X-ray diffraction patterns of class I (Fig. 3), it can be found that the PVDF2SiO₂-1 and PVDF4SiO₂-1 hybrid membranes possessed fewer crystalline domains than the other two, the order followed PVDF > PVDF1SiO₂-1 > PVDF2SiO₂-1 > PVDF4SiO₂-1. The calculation results of the MSD of the polymer chains (Fig. 4) showed that the chain mobility of the polymer segments followed the order of PVDF4SiO₂-1 > PVDF2SiO₂-1 > PVDF1SiO₂-1 > PVDF. The FFV of the PVDF/SiO₂ hybrid membranes of class I is larger than that of the PVDF control membrane and follow the order of PVDF4SiO₂-1 > PVDF2SiO₂-1 > PVDF1SiO₂-1 > PVDF. Compared with the change of the diffusion coefficients of the water molecules in the membranes, the results showed that the diffusion coefficients of water are positively correlated with the mobility of the PVDF chain, and the free volume of the membranes; the diffusion coefficients of water are negatively correlated with the crystalline domains of the polymer chain.

3.2 Class II: different size of SiO₂

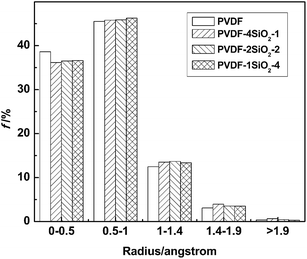
In class II, SiO₂-1, SiO₂-2, and SiO₂-4 were employed to construct PVDF4SiO₂-1, PVDF2SiO₂-2, and PVDF1SiO₂-4. The volume of SiO₂-2 is twice that of SiO₂-1 and SiO₂-4 is four times that of SiO₂-1. The concentration of silica is the same in these three hybrid membranes. In this part, the influences of the different sizes of silica on the interfacial morphology and transport properties of the membranes are studied.

3.2.1 Simulated X-ray diffraction patterns of the membranes. The simulated diffraction patterns of the hybrid membranes of class II are shown in Fig. 7. The peak intensity of the membranes follows the order PVDF > PVDF4SiO₂-1 > PVDF2SiO₂-2 ≈ PVDF1SiO₂-4, which reveals that the PVDF1SiO₂-4 and PVDF2SiO₂-2 hybrid membranes possess fewer crystalline domains than the other two. It indicated that the crystalline region decreased because the SiO₂ particles in the membrane interact with PVDF chains. As the radius of the SiO₂ is larger than 1.00 nm (the radius of SiO₂-2), it has little influence on the crystalline regions of the hybrid membrane because the big particles decreased the contact with the PVDF chain and the destruction of the crystalline regions is decreased correspondingly.

Fig. 6 The f (the ratio of the fractional free volume) of the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class I.

3.2.2 Mobility of the polymer chain. The MSD of the polymer chain in PVDF/SiO₂ hybrid membranes of class II is displayed in Fig. 8. It can be found that the polymer chain mobility of the hybrid membranes of class II is higher than that of the pure PVDF membrane and follows the order PVDF4SiO₂-1 > PVDF2SiO₂-2 > PVDF1SiO₂-4 > PVDF. This indicates that it has less influence on the mobility of the polymer chain when the SiO₂ particle size is bigger.

Fig. 7 Simulated X-ray diffraction patterns of the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class II.

3.2.3 Free volume of the membranes. The FFV of the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class II were also obtained using the probe method as mentioned in 3.1.4 and the results are listed in Table 3. It also shows that the FFV drops sharply as the probe size increased. The FFV of the PVDF/SiO₂ hybrid membranes of class II is larger than that of the PVDF control membrane and follow the order PVDF1SiO₂-4 > PVDF2SiO₂-2 > PVDF4SiO₂-1 > PVDF, which implies that the FFV increases with increasing size of silica.

Table 3 FFVs of the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class II

Radius of the probe (Å)	0	0.5	1.0	1.4	1.9
PVDF	24.09	14.79	3.83	0.82	0.08
PVDF4SiO2-1	24.45	15.49	4.18	0.93	0.07
PVDF2SiO2-2	24.56	15.59	4.33	0.97	0.10
PVDF1SiO2-4	24.56	15.68	4.44	1.12	0.16

---

The ratios of different radii of FFVs are shown in Fig. 9. The fraction of f_0–0.5 of the PVDF control membrane is larger than the hybrid membranes of class II. The fraction of FFV_0.5–1 is increased as the size of the silica is increased. It is easy to find out that PVDF1SiO₂-4 and PVDF2SiO₂-2 have larger size free volume voids. This can explain what we studied in 3.2.1, that PVDF1SiO₂-4 and PVDF2SiO₂-2 hybrid membranes possess fewer crystalline domains than the other two membranes.

Fig. 8 MSD of PVDF in the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class II.

3.2.4 Penetrant diffusion in membranes. In this part, the diffusion coefficients of water were studied by the method as mentioned in 3.1.5 (Table 4). The diffusion coefficients of water follow the order PVDF2SiO₂-2 > PVDF4SiO₂-1 > PVDF1SiO₂-4 > PVDF. The water molecules in the hybrid membranes possess higher mobility. Those in PVDF2SiO₂-2 possess the highest mobility. The chain mobility and the free volume are two key factors that affect the penetrant diffusivity in the membranes. A higher chain mobility induces a higher frequency of diffusion paths forming and disappearing. Higher FFVs always mean more accessible free volume voids in the membranes for penetrant diffusion. For the PVDF2SiO₂-2 model, it possesses a larger FFV and higher polymer chain mobility. Considering these two factors, the diffusion coefficient of water in the PVDF2SiO₂-2 model is higher than that of the other three membranes of class II.

Table 4 Diffusion coefficients of water in the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class II

Membranes	Diffusion coefficient
PVDF	1.80
PVDF4SiO2-1	3.73
PVDF2SiO2-2	4.50
PVDF1SiO2-4	2.23

---

3.2.5 The relationship between the diffusion coefficient and the other three properties (crystalline domains, mobility of the PVDF chain, and free volume of the membranes). There is an effect of the size of the silica particles on the size of the crystalline domain of membrane. The simulated X-ray diffraction data revealed that the PVDF1SiO₂-4 and PVDF2SiO₂-2 hybrid membranes possessed fewer crystalline domains than the other two, and the order followed PVDF > PVDF4SiO₂-1 > PVDF1SiO₂-4 ≈ PVDF2SiO₂-2. The calculation results of the MSD values of the polymer chains showed that the chain mobility of the polymer segments followed the order PVDF4SiO₂-1 > PVDF2SiO₂-2 > PVDF1SiO₂-4 > PVDF. This implies that the polymer chain possessed higher mobility when there were bigger SiO₂ particles in the membranes. The FFVs of the PVDF/SiO₂ hybrid membranes of class II are larger than that of the PVDF control membrane and follow the order PVDF1SiO₂-4 > PVDF2SiO₂-2 > PVDF4SiO₂-1 > PVDF. This indicates that SiO₂ particles with larger size made the hybrid membranes have larger FFVs. Compared with the change of the diffusion coefficients of water molecules in the membranes, on the whole the results also showed that the diffusion coefficients of water are positively correlated with the mobility of the PVDF chain, and the free volume of the membranes; the diffusion coefficients of water are negatively correlated with the crystalline domains.

Fig. 9 The f of the PVDF control membrane and PVDF/SiO₂ hybrid membranes of class II.

4 Conclusion

Two series of models (class I and class II) were constructed to investigate the effects of silica particles on the diffusion properties of water molecules in PVDF/SiO₂ membranes. The X-ray diffraction patterns, MSDs of polymer segments, FFVs of the hybrid membranes, and diffusion coefficients of water in the hybrid membranes were systematically investigated. It was observed that the diffusion coefficients of water in the membranes were larger than those in the control membrane. When the concentration of silica particles is different (class I), on the whole, the diffusion coefficient of water presented an increase as the concentration of silica increased (0–14.6 wt%). When the concentration range is from 3.7 to 7.3 wt%, the change of the diffusion coefficient is not obvious. With the same concentration of SiO₂ particles, when the size of the silica particles is different (class II), the diffusion coefficient of water presented an increase first and then decreases as the increase of the size of silica (radius: 0.8–1.3 nm). When the diameter of the silica is nearly 1 nm, the diffusion coefficient of water in the membranes is the largest (4.50 × 10⁻¹² m² s⁻¹). Furthermore, the results showed that the diffusion coefficients of water are positively correlated with the mobility of the PVDF chain and the free volume of the membranes; the diffusion coefficients of water are negatively correlated with the crystalline domains. Overall, MD simulations are a powerful tool to provide some theoretical details concerning the diffusion behavior of penetrant molecules in hybrid membranes, acting as a useful supplement and guidance to experimental investigation.

References

1. S. Y. Kwak, S. H. Kim and S. S. Kim, Environ. Sci. Technol., 2001, 35, 2388–2394.
2. R. K. Nagarale, G. S. Gohil, V. K. Shahi and R. Rangarajan, Macromolecules, 2004, 37, 10023–10030.
3. F. Peng, L. Lu, H. Sun, F. Pan and Z. Jiang, Ind. Eng. Chem. Res., 2007, 46, 2544–2549.
4. Y. Jia, Y. Zhang, R. Wang, J. Yi, X. Feng and Q. Xu, Ind. Eng. Chem. Res., 2012, 51, 12266–12273.
5. C. Chakraborty, P. K. Sukul, K. Dana and S. Malik, Ind. Eng. Chem. Res., 2013, 52, 6722–6730.
6. A. Walcarius, Chem. Mater., 2001, 13, 3351–3372.
7. K. Das, S. S. Ray, S. Chapple and J. Wesley-Smith, Ind. Eng. Chem. Res., 2013, 52, 6083–6091.
8. F. Pan, F. Peng, L. Lu, J. Wang and Z. Jiang, Chem. Eng. Sci., 2008, 63, 1072–1080.
9. Y. Tamai, H. Tanaka and K. Nakanishi, Macromolecules, 1994, 27, 4498–4508.
10. Y. Tamai, H. Tanaka and K. Nakanishi, Macromolecules, 1995, 28, 2544–2554.
11. Y. Tamai, H. Tanaka and K. Nakanishi, Fluid Phase Equilib., 1995, 104, 363–374.
12. M. Heuchel, D. Hofmann and P. Pullumbi, Macromolecules, 2004, 37, 201–214.
13. B. Sakintuna, E. Fakioglu and Y. Yȕrȕm, Energy Fuels, 2005, 19, 2219–2224.
14. W. Z. Lang, Z. L. Xu and H. Yang, et al., J. Membr. Sci., 2007, 288, 123–131.
15. X. C. Cao, J. Ma and X. H. Shi, et al., Appl. Surf. Sci., 2006, 253, 2003–2010.
16. A. Bottino, G. Capannelli and A. Comite, Desalination, 2002, 146, 35–40.
17. Y. Lu, S. L. Yu and B. X. Chai, Polymer, 2005, 46, 7701–7706.
18. D. J. Lin, C. L. Chang and L. P. Cheng, et al., Polymer, 2003, 44, 413–422.
19. T. Ogoshi and Y. Chujo, J. Polym. Sci. A: Polym. Chem., 2005, 43, 3543–3550.
20. H. Sun, Macromolecules, 1936, 28, 701–712.
21. H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364.
22. S. L. Mayo, B. D. Olafson and W. A. Goddard, J. Phys. Chem., 1990, 94, 8897–8909.
23. H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393.
24. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. Dinola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3960.
25. P. P. Ewald, Ann. Phys., 1921, 64, 253–287.
26. N. Karasawa and W. A. Goddard, Macromolecules, 1992, 25, 7268–7281.
27. H. Wang, L. Yao, B. Ding, J. Luo, G. Zhou and B. Jiang, Chem. J. Chin. Univ., 2013, 34, 1295–1302.
28. L. Yao, P. Chen, B. Ding, J. Luo, B. Jiang and G. Zhou, J. Mol. Model., 2012, 18, 4529–4545.
29. T. T. Moore and W. J. Koros, J. Mol. Struct., 2005, 739, 87–98.
30. R. K. Bharadwaj, R. J. Berry and B. L. Farmer, Polymer, 2000, 41, 7209–7221.
31. J. R. Fried and P. Ren, Comput. Theor. Polym. Sci., 2000, 10, 447–463.
32. J. R. Fried and D. K. Goya, J. Polym. Sci., Part B: Polym. Phys., 1998, 36, 519–536.
33. C. Nagel, E. Schmidtke, K. Günther-Schade, D. Hofmann, D. Fritsch, T. Strunskus and F. Faupel, Macromolecules, 2000, 33, 2242–2248.
34. D. Fragiadakis, P. Pissis and L. Bokobza, Polymer, 2005, 46, 6001–6008.
35. F. Peng, L. Lu, H. Sun, Y. Wang, J. Liu and Z. Jiang, Chem. Mater., 2005, 17, 6790–6796.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra09261b

---