Energetics of proton transfer in alkali carbonates: a first principles calculation

Abstract

Recent development of dual-phase ceramic–carbonate composite electrolytes for intermediate-temperature solid oxide fuel cells (SOFCs) has prompted a pressing question as to whether H⁺ can transfer in molten carbonates and play a role in the enhanced ionic conductivity and improved SOFC performance. In the present study, we use a first principles approach to examine the energetics of H⁺-transfer in CO₃²⁻, Li₂CO₃ crystals and (Li₂CO₃)₈ clusters. The results indicate that H⁺-transfer in solid carbonates is difficult, but very facile in a (Li₂CO₃)₈ cluster, a surrogate of molten carbonates.

---

1. Introduction

A focus of the current effort to commercialize solid oxide fuel cell (SOFC) technology is to lower the operating temperature to below 600 °C where high reliability and low cost can be achieved. The major barrier to the realization of reduced temperature SOFCs is the lack of high-conductivity electrolytes and high-activity catalytic cathodes. A noticeable development of the former in recent years is the use of dual-phase composites comprising a solid ionic conductor and carbonate as the intermediate-temperature (IT) electrolytes.^1–10 Testing of these composite electrolytes in a SOFC has yielded high power density in the IT range.^7–9 To understand the high performance, a number of ionic conduction mechanisms have been proposed. For example, Zhu et al.^3–5 proposed a binary O²⁻/H⁺ conduction mechanism to explain the enhanced conductivity for a ceria–carbonate electrolyte. Similarly, Li et al. proposed a ternary O²⁻/H⁺/CO₃²⁻ conduction mechanism to account for the enhanced conductivity and SOFC performance for a samarium-doped cerium oxide (SDC)/Li–Na–K carbonate composite.^8,9 Recently, we have also formulated several ionic conduction mechanisms to understand the enhanced ionic conductivity in the presence of water vapor in a BaZr_0.8Y_0.2O_3−δ (BZY) and a Li–K carbonate composite electrolyte.¹⁰

A close examination of the aforementioned ionic conduction mechanisms suggests that proton conduction in molten carbonates may play an important role in the enhanced ionic conductivity and subsequently SOFC performance. However, how protons transfer in molten carbonates remains mechanistically ambiguous at this point. To the best of our knowledge, there have been neither theoretical nor experimental investigations on proton transfer in molten carbonates in the open literature other than proton transfer in an aqueous KHCO₃ system.^11,12

In this study, we use first principles approach to calculating the energetics of proton transfer in three entities: CO₃²⁻, Li₂CO₃ crystal and (Li₂CO₃)₈ cluster to provide a theoretical ground for the understanding of enhanced ionic conductivity and improved SOFC performance observed in the experiments. A (Li₂CO₃)₈ cluster was employed to represent the state of an alkali molten carbonate.

2. Computational methods

2.1 Calculations for (CO₃)²⁻ and (CO₃H)⁻ ions, and periodic structures

All calculations for (CO₃)²⁻ and (CO₃H)⁻ ions, and periodic structures were performed using the Vienna Ab Initio Simulation Package (VASP), version 5.3.^13,14 The projector-augmented wave (PAW) method was used for calculating core and valence electron interactions,^15,16 while the Perdew–Burke–Ernzerhof (PBE) form of the generalized gradient approximation (GGA) was used to describe the exchange-correlation interaction.¹⁷ The cut-off energy of the plane wave basis representing valence electrons was set to 500 eV. The self-consistent field cycle convergence tolerance was set to 10⁻⁴ eV and the Hellmann–Feynman force on each atom was minimized to less than 0.02 eV Å⁻¹. The proton transport properties were modeled using a 3 × 2 × 2 k-point grid for a 96-atom supercell. The climbing image-nudged elastic band (CI-NEB) method¹⁸ was employed to find the minimum energy paths and transition states for proton transfer. A vacuum layer of 15 Å has been applied for (CO₃)²⁻ and (CO₃H)⁻ ions.

2.2 Calculations for (Li₂CO₃)₈ and [(Li₂CO₃)₈H]⁺ clusters

For cluster systems, combining SCAN with TS functions in Gaussian suite of quantum program can be easily used to search the transition state, while the IRC function can help judge the reaction direction. To illustrate that Gaussian is a valid method for calculating transition state and reaction direction, we also performed test calculations by VASP 5.3 (ref. 13 and 14) and Gaussian 09,¹⁹ respectively. The structures of (CO₃)²⁻ and (CO₃H)⁻ ions were optimized and the energy barrier of proton transfer in intra-carbonate ion (CO₃)²⁻ were calculated. It was found that the deviation between the two methods were generally small: ∼1% for bond length, 0.1–1.0% for bond angle, 14–16% for energy barrier. It is, therefore, reasonable to believe that Gaussian 09 can produce representative energy barrier of proton transfer in the (Li₂CO₃)₈ cluster.

All calculations for (Li₂CO₃)₈ and [(Li₂CO₃)₈H]⁺ clusters were performed by Gaussian 09 suite of quantum programs, including the geometry optimization, transition state search and intrinsic reaction coordinate (IRC) calculations. The geometries were optimized by using the generalized gradient approximation (GGA) based hybrid functional of B3LYP^20,21 in combination with the full-electron basis set with polarization functions of 6-31G(d)^22–24 to obtain accurate results. B3LYP has been proven to be reliable in treating electronic exchange and correlation over a wide range of molecular systems. The vibrational frequencies of each cluster were calculated at the same computational level as the geometry optimization, ensuring that the structures are located at a true minimum on the potential energy surface and the transition state is a first-order saddle point on the potential energy surface. All resulting energies contained the zero-point energy (ZPE) corrections. In addition, the interactions between proton and carbonate ions are orbital overlap and electrostatic interactions. Therefore, the dispersive interactions can be ignored in our calculations.

3. Results and discussion

3.1. Proton migration in CO₃²⁻ in gas phase

Before examining proton migration in gas-phase (CO₃)²⁻, we first optimized the structures of (CO₃)²⁻ and (CO₃H)⁻ ions. The bond distances and angles are shown in Fig. 1(a) and (b). Both structures feature a planar geometry. In (CO₃)²⁻ of D_3h symmetry, all the calculated C–O bond lengths are 1.295 Å, which reasonably agree well with the literature results of 1.306 Å (ref. 25) and 1.309 Å (ref. 26). All the bond angles of O–C–O are 120°. Addition of proton to the (CO₃)²⁻ forms planar (CO₃H)⁻ of C_s symmetry, where the bond angle of H–O–C is 101.2° and the bond length of O–H is 0.976 Å.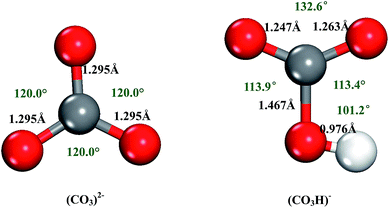

Fig. 1 The optimized structures of (CO₃)²⁻ and (CO₃H)⁻ ions. The grey, red, and white balls represent the carbon, oxygen, and hydrogen atom, respectively.

Fig. 2(a) and (b) shows the H⁺-migration in a gas-phase (CO₃)²⁻. Here, we select two representative motions: planar transfer between two oxygen atoms and rotation along one oxygen atom. The first motion is shown in Fig. 2(a), where H⁺ (in white color) migrates from O1 to O2. During this transfer, the bond between O1 and H⁺ is first broken, followed by H⁺ moving toward the mirror position between O1 and O2, namely the transition state. The bond between O2 and H⁺ is then reformed, completing the H⁺-transfer. We found that the energy barrier for H⁺-transfer between O1 and O2 was 0.89 eV.

Fig. 2 The energy barrier of proton transfer in the (CO₃)²⁻ ionic cluster. (a) H⁺-transfer between O1 and O2, (b) H⁺-transfer via rotation along the O1. The grey, red, and white balls represent the carbon, oxygen, and hydrogen atom, respectively.

Unlike the H⁺-migration through intra-oxygen shown in Fig. 2(a), Fig. 2(b) shows H⁺-transfer through H⁺-rotation along O1 atom. Likewise, a transition state was searched by NEB method. As shown in Fig. 2(b), H⁺ on the left side of O1 rotates along O1, passing through the transition state above the O1 atom, reaching the right side of O1. During this process, the bond between O1 and H⁺ remains, and the transfer only needs to overcome an energy barrier of 0.40 eV. Clearly, the rotation mechanism is energetically more favorable than the intra-oxygen transfer mechanism for H⁺-migration in (CO₃)²⁻. Such a low energy barrier also implies that lower thermal energy (or lower temperature) is needed to drive H⁺-migration in (CO₃)²⁻.

3.2. Proton migration in Li₂CO₃ crystal

We are also interested in H⁺-migration in a crystalline carbonate, the material of which under this study is lithium carbonate (Li₂CO₃) having a monoclinic structure and C2/c space group. The optimized crystal structure of a Li₂CO₃ is shown in Fig. 3. There are four formula units in a primitive cell as shown in Fig. 3(a). The calculated lattice parameters are a = 8.397 Å, b = 5.019 Å, c = 6.311 Å; α = 89.99°, β = 114.63°, γ = 90.00°, which agree reasonably well with the experimental values: a = 8.39 Å, b = 5.00 Å, c = 6.21 Å; α = 90.00°, β = 114.5°, γ = 90.00°.²⁷ To simulate the H⁺-transfer in Li₂CO₃, a supercell containing a 1 × 2 × 2 cell is constructed and shown in Fig. 3(b).

Fig. 3 The optimized triclinic crystal structure of Li₂CO₃; (a) primitive cell; (b) supercell structure in 1 × 2 × 2 array. The purple, red, and grey balls represent the lithium, oxygen, and carbon atom, respectively.

From analysis of the symmetry of the Li₂CO₃ crystal structure, four representative migration pathways of H⁺-transfer along a, b, c, and ca directions are considered, as shown in Fig. 4(a)–(d), respectively. In Fig. 4, [100], [010], [001], and [101] represent the directions of H⁺-transfer along a, b, c, and ca, respectively. On the other hand, [1̄00], [01̄0], [001̄] and [1̄01̄] represent the H⁺-transfer along -a, -b, -c, and -ca directions, respectively. Generally, there are three possible motions of H⁺ in Li₂CO₃: (1) rotation – the proton rotates around one oxygen ion while still remaining bonded to the oxygen ion; (2) intra-carbonate ion transfer – the proton moves from one oxygen ion to another oxygen ion of the same carbonate ion; (3) inter-carbonate ion transfer – the proton moves from one oxygen ion to another oxygen ion of a different carbonate ion. For convenience, we used small case letter a, b, c … to denote the possible proton locations and capital T and R to represent proton transfer between oxygen and rotation along one oxygen. For example, T_ab refers to proton transferring between two O atoms from a to b, and R_bc refers to proton rotation along one O from b to c. The energy barriers for H⁺-migration involved in these pathways are summarized in Tables 1–3.

Fig. 4 Schematic representations of H⁺-transfer along (a) [100], (b) [010], (c) [001] and (d) [101] directions, respectively. The primitive cell is indicated by dashed lines.

Table 1 Energy barriers of proton migration along the pathway [100] and [1̄00] direction

[100]	Tab	Tbc	Rcd	Tda
Barriers (eV)	0.85	0.78	0.58	0.90

---

[1̄00]	Tad	Rdc	Tcb	Tba
Barriers (eV)	0.79	0.58	0.84	0.85

---

Table 2 Energy barriers of proton migration along the pathway [010] and [01̄0] direction

[010]	Tef	Tfg
Barriers (eV)	0.37	1.10

---

[01̄0]	Tgf	Tfe
Barriers (eV)	0.83	0.60

---

Table 3 Energy barriers of proton migration along the pathway [001] and [001̄] direction

[001]	Thi	Rij	Tjh
Barriers (eV)	0.33	0.20	0.34

---

[001̄]	Thj	Rji	Tih
Barriers (eV)	0.21	0.48	0.18

---

Fig. 4(a) shows the H⁺-transfer pathway via T_ab → T_bc → R_cd → T_da along the [100] direction. From Table 1, the T_ab and T_ba pathways involve H⁺-transfer between two O of one (CO₃)²⁻ and present a higher migration energy barrier of 0.85 eV. By contrast, R_cd and R_dc pathways represent H⁺-transfer through rotation along one O of (CO₃)²⁻ and yield a lower migration energy barrier of 0.58 eV. These findings agree well with the results of H⁺-migration in a (CO₃)²⁻ at gas phase (see Section 3.1).

The H⁺-transfer along the [010] direction only includes two steps: inter-carbonate ion transfer (T_ef) and intra-carbonate ion transfer (T_fg). The former needs to overcome the energy barrier of 0.37 eV, and the latter needs to overcome a higher barrier of 1.10 eV. On the contrary, the highest energy barrier along [01̄0] direction is found to be 0.83 eV in the intra-carbonate ion transfer (T_gf) process.

Similarly, the pathway along the [001] direction can undergo by the following sequence: T_hi → R_ij → T_jh. The highest migration barriers are found to be 0.34 and 0.48 eV for [001] and [001̄] directions, respectively.

Furthermore, Fig. 4(d) shows the H⁺-transfer pathway via R_kl → T_lm → R_mn → T_no → R_op → T_pk along [101] direction. From Table 4, we can see that the R_kl yields the highest migration energy barrier of 1.13 eV along [101], followed by R_lk of 0.91 eV along [1̄01̄], T_lm and T_ml of 0.84 eV along [101] and [1̄01̄] direction, respectively.

Table 4 Energy barriers of proton migration along the pathway [101] and [1̄01̄] direction

[101]	Rkl	Tlm	Rmn	Tno	Rop	Tpk
Barriers (eV)	1.13	0.84	0.32	0.11	0.49	0.02

---

[1̄01̄]	Tkp	Rpo	Ton	Rnm	Tml	Rlk
Barriers (eV)	0.12	0.49	0.02	0.54	0.84	0.91

---

Comparison of the above energetics suggests that the H⁺-transfers in a crystalline Li₂CO₃ along [001] and [001̄] directions is more favorable than other directions. The reason for the favorable H⁺-migration stems from the relative crystallographic positions of (CO₃)²⁻ to c-axis. As is shown in Fig. 3, the (CO₃)²⁻ plane is perpendicular to c-axis along the [001] and [001̄], making the rotational H⁺-transfer geometrically easier. On the other hand, when the proton transfers between inter-carbonate ions, the carbonate ions also adjust their position accordingly, decreasing the energy barrier of H⁺-transfer. However, it is almost parallel to a-axis, b-axis and ac direction along the [100], [010], [101], [1̄00], [01̄0], and [1̄01̄] directions, such as T_ab, T_fg and T_lm, which requires H⁺ to transfer between two O in a (CO₃)²⁻. As aforementioned, H⁺-transfer via intra-oxygen mechanism has a higher energy barrier.

3.3. Proton migration in (Li₂CO₃)₈ cluster

Since the experiments that showed an enhanced ionic conductivity and improved SOFC performance involved molten carbonates, we are also interested in H⁺-transfer in the molten state of carbonates. Here we used a cluster of (Li₂CO₃)₈ to represent a disordered molten carbonate. Fig. 5 shows the structure of cluster (Li₂CO₃)₈ and the structural states of beginning, transitioning and ending phases of proton transfer in the (Li₂CO₃)₈ cluster together with the relative energies. The (Li₂CO₃)₈ clusters at the b3lyp/6-31g(d) level were first optimized. As illustrated in Fig. 5(a), each Li⁺ is bonded to three carbonate O²⁻, while each carbonate O²⁻ is connected to two Li⁺. Such a coordination is the same as those in the crystal structures of Li₂CO₃. In addition, the average bond length between Li⁺ and O²⁻ (d_Li-O) in (Li₂CO₃)₈ is calculated to be 1.948 Å, which agrees well with experimental values of 1.960 Å.²⁸ Our recent ab initio molecular dynamics (AIMD) study confirms that the volume expansion of Li₂CO₃ is only 3% at the temperature of 1300 K (calculated melting point ∼1000 K), implying that the Li–O bond length would not change significantly in the molten lithium carbonate. All evidences above suggest that using (Li₂CO₃)₈ to describe the structure of molten carbonates be reasonable.

Fig. 5 The structure of (Li₂CO₃)₈ cluster and the structural states of beginning, transitioning and ending phases of proton transfer in a [(Li₂CO₃)₈H]⁺ cluster together with the relative energies. The purple, grey, red, and white balls represent the lithium, carbon, oxygen, and hydrogen atom, respectively.

Next, the stable structure of [(Li₂CO₃)₈H]⁺ cluster is also obtained at the b3lyp/6-31g(d) level. To examine how the proton migration takes place on the atomic scale, we first locate a transition state (Fig. 5(c)) through the SCAN and TS functions implanted in Gaussian 09 package, followed by IRC calculation. Then, we optimized the two end point structures of IRC to obtain the accurate structures of reaction and product, as shown in Fig. 5(b) and (d). As seen from Fig. 5, the H⁺ bonds with Oa as the reactant and bonds with Ob as the product. The IRC calculations specify that the H⁺ first departs from Oa to the middle point between Oa and Ob, reaching the TS. During this process, the bond between H⁺ and Oa is enlarged from 1.018 Å to 1.237 Å with a very small energy barrier of 0.08 eV. Then the H⁺ separates from Oa and continues to move towards Ob. Meanwhile, the bond length of H⁺-Oa increases from 1.237 Å to 1.399 Å, whereas the bond length of H⁺-Ob reduces from 1.170 Å to 1.069 Å, thus completing a single H⁺-transfer process. In addition, the low TS-to-product energy barrier also suggests that the transition from product to reactant is a reversible process, which further implies that continuous H⁺-transfer in (Li₂CO₃)₈ cluster or molten carbonate is indeed very feasible.

4. Conclusions

In conclusion, the H⁺-transfer in (CO₃)²⁻, Li₂CO₃ and (Li₂CO₃)₈ cluster were investigated by first principles calculation. On the basis of the transition state theory and calculated energetics, we found that H⁺-rotation along one oxygen atom on (CO₃)²⁻ was much easier than H⁺-transfer between two oxygen atoms on (CO₃)²⁻, indicating that a faster H⁺-transfer relies upon the orientation of (CO₃)²⁻. Four plausible H⁺-transfer pathways in a crystalline Li₂CO₃ were also analyzed. The calculated energetics suggested that the [001] and [001̄] directions (c-axis) were the most favorable pathways for H⁺-transfer in Li₂CO₃. The lower energy barrier was originated from the crystallographic orientation of (CO₃)²⁻ perpendicular to c-axis, making H⁺-rotation along O much easier. Furthermore, (Li₂CO₃)₈ cluster was used to simulate H⁺-transfer in disordered molten carbonates. The extremely low H⁺-migration energy barrier indicated that the H⁺-transfer in (Li₂CO₃)₈ cluster and therefore molten carbonate was a very facile process. Overall, the computational results obtained clearly support the experimental observations that fast H⁺-transport in molten carbonate is very feasible for dual-phase ceramic-carbonate electrolytes used in IT-SOFCs.

Acknowledgements

Financial supports from NSF (CBET-1340269, CBET-1264706), U. S. Army Research Office (W911NF-10-R-006 and W911NF-13-1-0158) are greatly appreciated.

References

1. A. Bodén, J. Di, C. Lagergren, G. Lindbergh and C. Y. Wang, J. Power Sources, 2007, 172, 520–529.
2. B. Zhu, X. Liu, P. Zhou, X. Yang, Z. Zhu and W. Zhu, Electrochem. Commun., 2001, 3, 566–571.
3. B. Zhu, J. Power Sources, 2003, 114, 1–9.
4. B. Zhu, X. T. Yang, J. Xu, Z. G. Zhu, S. J. Ji, M. T. Sun and J. C. Sun, J. Power Sources, 2003, 118, 47–53.
5. J. Di, M. Chen, C. Wang, J. Zheng, L. Fan and B. Zhu, J. Power Sources, 2010, 195, 4695–4699.
6. L. Fan, G. Zhang, M. Chen, C. Wang, J. Di and B. Zhu, Int. J. Electrochem. Sci., 2012, 7, 8420–8435.
7. Y. Li, Z. Rui, C. Xia, M. Anderson and Y. S. Lin, Catal. Today, 2009, 148, 303–309.
8. C. Xia, Y. Li, Y. Tian, Q. Liu, Y. Zhao, L. Jia and Y. Li, J. Power Sources, 2009, 188, 156–162.
9. C. Xia, Y. Li, Y. Tian, Q. Liu, Z. Wang, L. Jia, Y. Zhao and Y. Li, J. Power Sources, 2010, 195, 3149–3154.
10. X. Li, N. Xu, L. Zhang and K. Huang, Electrochem. Commun., 2011, 13, 694–697.
11. F. Fillaux, J. Mol. Struct., 2007, 844–845, 308–318.
12. P. D. Dopieralski, Z. Latajka and I. Olovsson, Acta Crystallogr., Sect. B: Struct. Sci., 2010, 66, 222–228.
13. G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558–561.
14. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186.
15. P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979.
16. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775.
17. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
18. G. Henkelman, B. P. Uberuaga and H. Jonsson, J. Chem. Phys., 2000, 113, 9901.
19. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009.
20. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
21. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
22. A. D. McLean and G. S. Chandler, Chem. Phys., 1980, 72, 5639–5648.
23. K. Raghavachari, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
24. T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301.
25. W. R. Carper, P. G. Wahlbeck and T. R. Griffiths, J. Phys. Chem. B, 2012, 116, 5559–5567.
26. C. Y. Qin and A. Gladney, Comput. Theor. Chem., 2012, 999, 179–183.
27. M. H. Brooker and J. B. Bates, J. Chem. Phys., 1971, 54, 4788.
28. A. Grzechnik, P. Bouvier and L. Farina, J. Solid State Chem., 2003, 173, 13–19.

---