Au@ZnO hybrid nanostructures: correlation between morphology and optical response†
Abstract
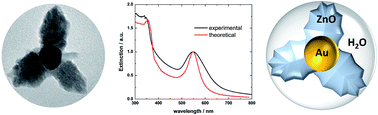
Au@ZnO hybrid nanostructures (HNs) have been synthesized in aqueous media by implementing a simple chemical methodology. These HNs consist of 40 nm mean size almost spherical Au cores, over which the heterogeneous formation of ZnO is observed. By increasing the concentration of ZnO precursors in the system, it is possible to change the morphology of the material formed over the Au core from branched to shell like structures, which, in turn, significantly modifies the extinction properties of the naked Au core nanoparticles. This effect has been rationalized by means of electrodynamics simulations based on two different approaches: the Mie theory for coated spheres and the Discrete Dipole Approximation (DDA). The changes measured in the extinction spectra as the amount of ZnO formed around the Au cores increases are properly described by both methodologies, while the good correlation between experimental and theoretical spectra suggest that the ZnO material includes a significant amount of water. Furthermore, based on the Mie theory results, a graphical method was implemented which allows us to predict the main morphological parameters of the Au@ZnO HNs. In addition, the combination of optical measurements, morphological characterization and DDA modeling allowed us to estimate that the water content of the shell surrounding the metallic core is 65%. The methodology presented in this work provides a useful tool to characterize the structural properties of HNs and can be straightforwardly generalized to other systems.

 Please wait while we load your content...
Please wait while we load your content...