Electronic and charge transport properties of dimers of dithienothiophenes: effect of structural symmetry and linking mode
Abstract
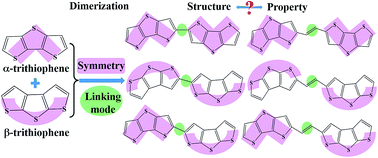
The electronic structures and charge transport properties of a series of dimers of dithienothiophenes are investigated by means of quantum chemical calculations. To gain a better understanding of the effects of the structural symmetry and linking mode on the dimers, the geometrical structures, molecular reorganization energies upon gaining or losing electrons, molecular ionization potentials (IPs) and electron affinities (EAs), molecular aromaticities, frontier molecular orbitals, as well as charge mobilities are analyzed in detail to determine the structure–property relationships for the investigated dimers of dithienothiophenes. The calculated results show that the vinylene-linked dimers have advantages over the directly single-bond linked dimers because of the large extent of π conjugation and thus enhanced π–π stacking interactions in their crystal structures. The molecular symmetry could affect the electron density distributions in the molecules, and further determine the molecular orientations and intermolecular arrangements. High molecular symmetry could facilitate the molecular packing in order, thus enhancing the charge transport. The theoretical characterization of these dimers in combination with experimental results indicate that highly symmetrical vinylene-bridged dimers could be promising candidates for transistor applications, and shed light on the molecular design of high performance materials.

 Please wait while we load your content...
Please wait while we load your content...