Synthesis, structure, characterization and theoretical studies of NLO active furan-2-carbohydrazide monohydrate derivative single crystals

Abstract

Single crystals of (E)-N′-(4-isopropylbenzylidene)furan-2-carbohydrazide monohydrate were grown by the slow evaporation solution growth technique from ethanol at room temperature. The crystals belong to the orthorhombic system with noncentrosymmetric space group P2₁2₁2₁. The crystallinity of the material was confirmed by powder X-ray diffraction analysis. The functional groups present in the molecule are identified by FT-IR analysis and the band gap energy is estimated using diffuse reflectance data by the application of Kubelka–Munk algorithm. Theoretical calculations were performed using a density functional theory (DFT) method to derive the optimized geometry, dipole moment, polarizability, HOMO–LUMO energies at different levels, molecular electrostatic potential, excited state energy, oscillator strength, Mulliken charge population and first-order molecular hyperpolarizability, (β) (>58 times of urea). The intermolecular hydrogen bonding interactions are analyzed by Hirshfeld surface analysis and fingerprint plots. The second harmonic generation efficiency (SHG) is estimated using the Kurtz and Perry powder technique and it reveals NLO (nonlinear optical) character. As-grown crystals were further characterized by NMR, mass spectrometry and elemental analysis.

---

1. Introduction

The hydrazone functional group is ubiquitous in various fields ranging from organic synthesis,^1–4 medicinal chemistry,^5–10 supramolecular chemistry^11–13 and hole-transporting materials¹⁴ to nonlinear optics.¹⁵ Hydrazones are used as photochemically controlled configurational switches, metallo-assemblies and sensors.^16–19 The hydrazone group plays an important role in antimicrobial activity and possesses interesting antibacterial, antifungal^20–22 and anti-tubercular activities^23–28. Aromatic hydrazone molecules dispersed in a binder polymer are used as the main constituent of electrophotographic devices due to their excellent hole-transporting properties and relatively simple synthesis.^29–32 Recently, we have reported the synthesis, growth, characterization and theoretical studies of some hydrazones.^33–35 The synthesis, structure and characterization of (E)-N′-(4-isopropylbenzylidene)furan-2-carbohydrazide monohydrate have not been reported so far to the best of our knowledge. In the present study, we report the synthesis, growth, structure, characterization, dipole moment, first-order molecular hyperpolarizability, and Hirshfeld surface analysis of (E)-N′-(4-isopropylbenzylidene)furan-2-carbohydrazide monohydrate and the experimental data are compared with theoretical studies.

2. Experimental

2.1. Synthesis

(E)-N′-(4-Isopropylbenzylidene)furan-2-carbohydrazide monohydrate (IFC) was synthesized by mixing stoichiometric amounts of p-isopropylbenzaldehyde and furan-2-carbohydrazide in the molar ratio of 1 : 1 (Scheme 1). The reactants were dissolved in ethanolic medium and stirred for 4–5 h to form aryl acid hydrazone. The product formation was identified by thin layer chromatography. The reaction mixture was then poured in ice cold water and the precipitate obtained was filtered and dried. Purity of the compound was improved by recrystallization process using ethanol as a solvent.

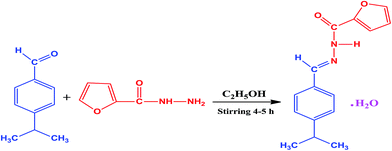Scheme 1

2.2. Crystal growth

IFC single crystals were grown using the slow evaporation solution growth technique at room temperature. A saturated solution of IFC in ethanol was prepared and the solution was stirred for 3–5 h at room temperature to obtain a homogenous solution. A beaker containing solution was tightly covered with a thin polythene sheet to control the evaporation rate of the solvent and kept undisturbed in a dust free environment. Numerous needle like crystals were formed at the bottom of the container due to spontaneous nucleation. Macroscopic defect-free crystals of IFC were harvested after 7–9 d.

2.3. Characterization techniques

The structural analysis was carried out for a selected sample of approximately 0.35 × 0.25 × 0.30 mm³ size using a BRUKER AXS (Kappa APEXII) X-ray diffractometer. Single crystal XRD data were collected on a diffraction system that employs graphite monochromated Mo Kα radiation (λ = 0.71073 Å). The powder XRD analysis was performed using a Philips X'pert Pro Triple axis X-ray diffractometer using a wavelength of 1.540 Å with a step size of 0.008 Å and the samples were examined with Cu Kα radiation in 2θ range of 10−50°. FT-IR spectra were recorded using an AVATAR 330 FT-IR by KBr pellet technique in the spectral range of 400–4000 cm⁻¹. The NMR spectra were recorded on BRUCKER AVIII 500 MHz NMR spectrometer operating at 500.18 MHz for ¹H and 125.78 MHz for ¹³C using standard parameters. The IFC is dissolved in 0.5 mL of CDCl₃ solvent and TMS (tetramethylsilane) was used as an internal standard. Mass spectral analysis of IFC was recorded on a VARIAN SATURN 2000 GC-MS/MS spectrometer using electron impact technique by dissolving about 1 mg of compound in 5 mL of spectral grade methanol. A CARY−5E UV-vis spectrophotometer was used for the UV-vis studies. Elemental data are collected by FLASH EA 1112 series of CHN analysis.

2.4. Computational studies

All the theoretical calculations were performed using the GAUSSIAN 09W³⁶ program package on a personal computer without any constraints on the geometry using density functional group theory (DFT) with B3LYP method 6-31G(d,p) as the basis set.³⁷ By the use of the GAUSSVIEW 5.0 molecular visualization program³⁸ the optimized structure of the molecule has been visualized. The theoretical electronic excitation energies, absorption wavelengths and oscillator strengths were calculated by the ZINDO/TD-SCF/CIS (DFT) method. HOMO and LUMO energies at different levels, molecular electrostatic potential, Mulliken charge population have been computed by B3LYP/DFT method. Polarizability and first-order molecular hyperpolarizability were calculated by using finite field method as default. Hirshfeld surfaces and fingerprint plots were generated from the crystal data using the DFT method with 6-31G(d,p) as basis set. Deformation density is generated from CrystalExplorer (Version 3.1), using DFT method with 6-31G(d,p) as basis set.

3. Results and discussion

3.1. FT-IR

The characteristic vibrational patterns observed in the FT-IR spectrum support the structure of the compound as shown in Fig. 1. The absorption band at 1643 cm⁻¹ is due to C=O stretching vibration. The absorption band around 3424 cm⁻¹ is due to NH stretching vibration. The C=N stretching vibration appeared as sharp intensity band around 1616 cm⁻¹. An absorption band in the region 3112 and 3134 cm⁻¹ are due to C–H stretching vibration of aromatic ring. The band at 1521 and 1473 cm⁻¹ are due to C=C stretching frequency of aromatic region. The absorption band around 1019 cm⁻¹ is due to O=C–N stretching vibrations and the peak at 745 cm⁻¹ is due to aromatic C–H out of plane bending vibrations. The observed FT-IR vibrational bands of IFC are listed in Table S1 (see ESI†).

Fig. 1 FT-IR spectrum of IFC.

3.2. Optical studies

The optical absorption spectrum shows the absorption is minimum in the visible region and cut-off wavelength is ∼397 nm. The Kubelka–Munk theory³⁹ provides a correlation between reflectance and concentration. The concentration of an absorbing species can be determined using the Kubelka–Munk formula,

F(R) = (1 − R)²/2R = α/s = Ac/s (1)

where F(R) is Kubelka–Munk function, R is the reflectance, s is scattering coefficient, A is the absorbance and c is concentration of the absorbing species. The direct and indirect band gap energies obtained from the intercept of the resulting straight lines with the energy axis at [F(R)hv]² = 0 and [F(R)hv]^1/2 = 0 are 3.39 eV (direct) and 3.25 eV (indirect) respectively as shown by Tauc plots in Fig. S1 (see ESI†).

The optical absorbance spectrum of IFC was recorded in the spectral range of 200 to 450 nm as shown in Fig. 2d. It displays the absorption spectrum of IFC at different concentrations 0.1, 0.2 and 0.3 M in ethanol medium. It exhibits a strong absorption maximum at ∼307 and 311 nm in the visible region. Theoretical values of UV-vis spectral analysis, calculated by ZINDO/TD-SCF/CIS method are summarized in Table 1. The theoretical spectra of IFC are shown in Fig. 2a–c and it is observed that TD-SCF method closely resembles with the experimental one.

Fig. 2 Excitation energies of IFC (a) ZINDO (b) TD-SCF (c) CIS and (d) experimental (0.1 M (black color), 0.2 M (red color) and 0.3 M (blue color)).

Table 1 Theoretical electronic absorption spectral values of IFC

DFT Method	Wavelength (λmax, nm)	Excitation energies (eV)	Oscillator strengths (f)
ZINDO	339.43	3.3943	0.9186
TD-SCF	329.85	3.2985	1.0986
CIS	244.62	2.4462	1.4345
Experimental
0.1 M	307.94	3.0794	0.8872
0.2 M	311.24	3.1124	1.3377
0.3 M	311.24	3.1124	1.7604

---

3.3. Thermal analysis

In order to test the thermal stability of IFC the thermogravimetric analysis (TG) and differential thermal analysis (DTA) have been carried out simultaneously. The TG/DTA response curve is shown in Fig. 3. In DTA curve the endothermic peak observed at 88.6 °C is attributed to melting of the IFC crystal. In the TG curve the major weight loss is from 250 to 300 °C indicates the decomposition (297 °C) of the sample. In DTA curve the endothermic peak observed at 112 °C is attributed to removal of water molecule present in IFC crystal. No exothermic or endothermic peak was observed below the melting point endotherm, indicating the absence of any isomorphic phase transition in the sample. The endothermic peak shows good degree of crystallinity of the as-grown material.

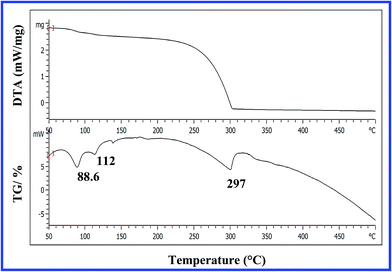Fig. 3 TG-DTA curve of IFC.

3.4. X-ray diffraction analysis

As-grown IFC crystal was finely powdered and subjected to powder XRD analysis. The indexed powder XRD pattern of IFC is shown in Fig. S2 (see ESI†). The well defined Bragg's peaks at specific 2θ angles show high crystallinity of the material. It belongs to the orthorhombic system with noncentrosymmetric space group P2₁2₁2₁. The ORTEP, packing diagram and optimized molecular structure are shown in Fig. 4 and the crystal data are given in Table 2. The optimized molecular structure of IFC (Fig. 4b) closely resembles the displacement ellipsoid diagram (Fig. 4a). It adopts an E configuration about the central C6=N2 double bond. The hydrazine group is twisted slightly with a N1–N2–C6–C7 torsion angle of −174.1 (3)°. In the crystal structure, molecules are linked through intermolecular C–H⋯O, N–H⋯O, O–H⋯O and C–H⋯N hydrogen bonds (Fig. 4d). The hydrogen bond symmetry is listed in Table 3. The Cartesian coordinate axis is shown in Fig. 4c. The agreement between the theoretical and experimental results has been expressed by root mean square (RMSD) deviationwhere n is the number of the experimental or calculated data. The negligible RMSD value suggests close agreement between calculated (theoretical) and experimental (single crystal XRD) values (Table 4). Systematic error is generally caused by neglecting anharmonicity and electron correlation.

Fig. 4 Molecular structure of IFC (a) ORTEP (b) optimized (c) Cartesian coordinate axes and (d) packing diagram.

Table 2 Crystal data and structure refinement for IFC

Empirical formula	C15H18N2O3
Formula weight	273.15
Temperature	566(2) K
Wavelength	0.71073 Å
Crystal system, space group	Orthorhombic, P212121
Unit cell dimensions	a = 4.715(2) Å, α = 90°
	b = 12.331(5) Å, β = 90°
	c = 24.742(11) Å, γ = 90°
Volume	1438.6(11) Å^3
Z, calculated density	4, 1.267 Mg m^−3
Absorption coefficient	0.089 mm^−1
F(000)	584
Crystal size	0.35 × 0.25 × 0.30 mm^3
Theta range for data collection	1.646 to 25.989°
Limiting indices	−5 ≤ h ≤ 5, −15 ≤ k ≤ 15, −30 ≤ l ≤ 30
Reflections collected/unique	14 732/2806 [R(int) = 0.0426]
Completeness to theta = 25.99	99.9%
Refinement method	Full-matrix least-squares on F^2
Data/restraints/parameters	2806/0/253
Goodness-of-fit on F^2	1.089
Final R indices [I > 2sigma(I)]	R1 = 0.0499, wR2 = 0.1057
R Indices (all data)	R1 = 0.0616, wR2 = 0.1108
Largest diff. peak and hole	0.174 and −0.146 e Å^−3

---

Table 3 Hydrogen bonds geometry of IFC (Å, °)^a

D–H⋯A	d(D–H)	d(H⋯A)	D(D⋯A)	<(DHA)
a Symmetry transformations used to generate equivalent atoms: #1 − x, y + 1/2, −z + 3/2 #2 x + 1, y, z.
C(6)–H(6)⋯O(3)#1	1.01(3)	2.49(3)	3.293(4)	136(2)
C(3)–H(3)⋯O(3)	0.92(3)	2.84(3)	3.409(4)	121(2)
N(1)–H(1)⋯O(3)#1	0.91(3)	1.98(3)	2.856(4)	164(3)
O(3)–H(3A)⋯O(2)	0.84(5)	2.04(5)	2.872(4)	170(4)
C(1)–H(1A)⋯N(2)#1	0.90(4)	2.78(4)	3.684(5)	176(4)
C(1)–H(1A)⋯O(2)#1	0.90(4)	2.70(4)	3.280(4)	123(3)
O(3)–H(3B)⋯N(2)#2	0.87(6)	3.14(6)	3.801(4)	134(5)
O(3)–H(3B)⋯O(2)#2	0.87(6)	2.00(6)	2.852(4)	167(5)

---

Table 4 Optimized structural parameters of IFC [bond lengths (Å) and bond angles (°)]

Parameters	single crystal XRD data	Theoretical data
Bond length
O(1)–C(1)	1.363(4)	1.3628
O(1)–C(4)	1.365(3)	1.3653
N(1)–C(5)	1.343(4)	1.3436
N(1)–N(2)	1.383(3)	1.3833
N(1)–H(1)	0.91(3)	0.9108
N(2)–C(6)	1.278(4)	1.2785
O(2)–C(5)	1.236(3)	1.2365
C(5)–C(4)	1.467(4)	1.467
C(7)–C(12)	1.384(5)	1.3829
C(7)–C(8)	1.390(5)	1.3911
C(7)–C(6)	1.464(4)	1.4647
O(3)–H(3A)	0.84(5)	0.8425
O(3)–H(3B)	0.87(6)	0.8732
Bond angle
C(1)–O(1)–C(4)	106.3(3)	106.3158
C(5)–N(1)–N(2)	119.3(3)	119.3252
C(5)–N(1)–H(1)	119(2)	119.025
N(2)–N(1)–H(1)	121(2)	121.5703
C(6)–N(2)–N(1)	114.5(3)	114.4594
O(2)–C(5)–N(1)	123.9(3)	123.9185
O(2)–C(5)–C(4)	120.0(3)	120.0395
N(1)–C(5)–C(4)	116.0(3)	116.0419
C(12)–C(7)–C(8)	117.4(3)	117.4692
C(12)–C(7)–C(6)	122.6(3)	122.6284
C(8)–C(7)–C(6)	119.9(3)	119.8598
H(3A)–O(3)–H(3B)	103(4)	102.8523
C(3)–C(4)–O(1)	109.9(3)	109.9057
C(3)–C(4)–C(5)	131.5(3)	131.5531
O(1)–C(4)–C(5)	118.5(2)	118.5359
N(2)–C(6)–C(7)	121.5(3)	121.4435
N(2)–C(6)–H(6)	122.0(18)	122.0234
C(7)–C(6)–H(6)	116.4(17)	116.4618
C(11)–C(12)–C(7)	121.0(3)	120.9867
C(11)–C(12)–H(12)	122(2)	122.5636
C(9)–C(10)–C(11)	116.8(3)	116.7635
C(9)–C(10)–C(13)	119.9(3)	119.8732
C(11)–C(10)–C(13)	123.3(3)	123.3129

---

3.5. Nonlinear optical property (NLO)

NLO efficiency of IFC at the molecular level is confirmed by the computational studies. The requirement of the noncentrosymmetry is not restricted to the molecular level, but also applies to the macroscopic nonlinear susceptibility. Not all organic materials display second order NLO properties. A common way to design second order NLO activity is to develop noncentrosymmetric π-conjugated systems that display efficient charge transfer from the periphery to the centre of the molecules. Noncentrosymmetric structure facilitates facile charge transfer. Recently, research has been focused on the effect of donor or acceptor substitution and elongation of the conjugation path length to demonstrate the engineering guidelines for enhancing molecular optical nonlinearities.

Recently, several experimental works^40–42 have proved that intermolecular interaction has important effects on electric hyperpolarizabilities which are related to the nonlinear optical (NLO) phenomena.⁴³ Consequently, interaction hyperpolarizability, which is an effect of intermolecular interaction on hyperpolarizability, has attracted increasing interest in recent years. Hydrogen bonding has a clear effect on increasing the hyperpolarizability value, resulting in enhanced NLO activity because of facile charge transfer.

Quantum mechanical calculations are used for predicting the molecular NLO properties of molecules. First hyperpolarizability is a third rank tensor that can be described by 3 × 3 × 3 matrix. The 27 components of the 3D matrix can be reduced to 10 components due to the Kleinman symmetry.^44,45 It can be given in the lower tetrahedral format.

E = E⁰ − μ_αF_α − 1/2α_αβF_αF_β − 1/6β_αβγF_αF_βF_γ + … (3)

where E⁰ – is the energy of the unperturbed molecule, F_α – the field at the orgin of μ_α, α_αβ and β_αβγ are the components of dipole moment, polarizability and first order hyperpolarizabilities respectively. α, β and γ labels are x, y and z components, respectively.

β_(tot) = (β_x² + β_y² + β_z²)^1/2 (4)

β_x = β_xxx + β_xyy + β_xzz (5)

β_y = β_yyy +β_xxy + β_yzz (6)

β_z = β_zzz + β_xxz + β_yyz (7)

The Cartesian coordinate axis is shown in Fig. 6c. It is clearly visible that the blue color vector line oriented through the X-axis. Therefore, the delocalization of the electron cloud is more towards X-axis direction. It is noticed that β_tot has its largest component of β_xxx along X-direction indicating that the delocalization of the electron cloud is more in that direction (Table 5).

Table 5 The calculated dipole moment (in D), β components (a.u.), β_tot value (in esu) and α components (a.u.), α_tot value (in esu) IFC

a βtot (1 a.u. = 8.641 × 10^−33 esu).
First-order molecular hyperpolarizability
βxxx	−1793.969
βxxy	547.339
βxyy	−39.146
βyyy	−99.256
βxxz	−1.177
βxyz	3.409
βyyz	18.579
βxzz	19.298
βyxx	−7.778
βzzz	18.641
βtot (×10^−30)^a	16.358
Polarizability
αxx	371.295
αxy	1.716
αyy	183.767
αxz	−0.398
αyz	1.842
αzz	80.966
αtot (×10^−24)	31.419
Dipole moment
μx	−1.4591
μy	−4.8171
μz	−1.4551
μ	5.2393

---

The calculated polarizability (α), first-order molecular hyperpolarizability (β) and dipole moment (μ) of the specimen are 31.419 × 10⁻²⁴ esu, 16.358 × 10⁻³⁰ esu (β value of urea is 0.382 × 10⁻³⁰ esu obtained by DFT/6-31G (d,p) method) and 5.2393 D respectively and the derived components are listed in Table 5. The β value of IFC is ∼58 times of urea and the maximum value of β is due to the nonzero μ values. High β is associated with high charge transfer.

Experimentally, second harmonic generation (SHG) efficiency was estimated by the Kurtz and Perry⁴⁶ technique. Potassium dihydrogen phosphate (KDP) sample was used as reference material (I_2ω of KDP = 55 mV) and the powder SHG efficiency of IFC was found to be twice that of KDP (I_2ω = 110 mV). High β with high SHG activity clearly evidence that IFC is a promising NLO material. It is interesting to observe that most of the hydrazones we reported previously possess molecular level nonlinearity but it is not sustained at the macro level (Table 6).

Table 6 NLO properties of some hydrazones

Compound	βtot (×10^−30) esu	SHG (I2ω)	Ref.
4-Benzoylpyridine isonicotinyl hydrazone monohydrate	2.799 (∼10 times of urea)	0	33
Benzophenone-2-furoyl hydrazone	0.817 (∼2.5 times of urea)	0	34
(E)-N′-(Diphenylmethylene)isonicotinohydrazide dihydrate	1.673 (∼5 times of urea)	0	35
(E)-N′-(4-Isopropylbenzylidene)furan-2-carbohydrazide monohydrate	16.354 (∼58 times of urea)	2 times of KDP	Present work

---

3.6. Frontier molecular orbital analysis (FMO)

Fig. 5 shows the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of IFC at different energy levels. The frontier orbital gap facilitates in characterizing the chemical reactivity and kinetic stability of the molecule. The HOMO is the orbital that primarily acts as an electron donor and the LUMO is the orbital that mainly acts as an electron acceptor. The total energy, HOMO−4, HOMO−3, HOMO−2, HOMO−1, HOMO and LUMO, LUMO+1, LUMO+2, LUMO+3, LUMO+4 energies, the energy gap, the dipole moment (D) for the IFC are calculated using B3LYP/6-31G(d,p) as basis set and 2D images of orbitals computed in gaseous state are shown in Fig. 5. The red color indicates the positive value and the green color indicates the negative value of wavefunction. It is clear from Fig. 5, the HOMO is localized on benzene, C=N, N–H and furoyl C=C group and LUMO is localized on N–NH, C=O, furoyl ring, while HOMO−1 is localized on furoyl moiety whereas LUMO+1 is localized almost on the whole molecule. The HOMO−2 is localized on the furoyl ring, LUMO+2 is localized almost on the benzene ring. The HOMO−3 is localized on the C=C group in benzene ring, LUMO+3 is localized on the C–H group, central part of C=N–N–H–C=O and furoyl ring. Likewise the HOMO−4 is localized on the furoyl ring containing O=C–NH–N=C– group and LUMO+4 is localized on the whole molecule. Both the HOMOs and the LUMOs are mostly π-anti-bonding type orbitals. All orbitals are plotted at an isosurface value 0.02 a.u. The calculated energy values of HOMO, −1, −2, −3, −4 levels are −0.22130, −0.25271, −0.25636, −0.25944,−0.27333 a.u. respectively and LUMO, +1, +2, +3, +4 levels are −0.06694, −0.03261, −0.00343, 0.03168, 0.04852 a.u., respectively. Also, the value of energy gap between the HOMO and LUMO is 0.1544 in a.u. Small HOMO–LUMO gaps result in more polarizability and hence this hydrazone is a promising NLO material.

Fig. 5 Frontier molecular orbitals HOMO−i and LUMO+i where i = 1,2,3,4 with their orbital energies (eV) and orbital energy gaps (eV).

3.7. Mulliken population analysis

In the application of quantum mechanical calculations to molecular systems, the calculation of effective atomic charge plays an important role. Mulliken atomic charges are calculated by determining the electron population of each atom as defined by the basis function. Fig. 6a and b show the Mulliken atomic charges and plots of IFC. From the atomic charge values the oxygen (O1, O4 and O36), nitrogen (N2 and N3) and carbon (C9, C11–C14 and C16–C19) in IFC had a large negative charge and behaved as electron donors. The remaining atoms (all H atoms and C5–C8, C10 and C15) are acceptors exhibiting positive charge. The negative charges on nitrogen/oxygen, which is a donor atom and net positive charge on hydrogen atom, which is an acceptor atom suggest the presence of intra- and intermolecular hydrogen bonding interactions. The Mulliken charge population values are given in Table 7. Hydrogen bonding interactions are clearly shown by the 3D images of ORTEP and packing diagram of single crystal X-ray diffraction data (Fig. S3 (a and b)) (see ESI†).

Fig. 6 (a) Mulliken atomic charge distribution and (b) Mulliken plot of IFC (c) Cartesian coordinate vector axis (blue color) of IFC.

Table 7 Mulliken charges of IFC

Atoms	Charge/(e)
O1	−0.52583
N2	−0.5436
N3	−0.1206
O4	−0.44154
C5	0.555386
C6	0.099331
C7	0.196743
C8	0.010692
C9	−0.0723
C10	0.137649
C11	−0.06155
C12	−0.1601
C13	−0.11449
C14	−0.12202
C15	0.191961
C16	−0.11435
C17	−0.05175
C18	−0.35081
C19	−0.36792
H20	0.109637
H21	0.128354
H22	0.312974
H23	0.095355
H24	0.092282
H25	0.12835
H26	0.054127
H27	0.069361
H28	0.124311
H29	0.141999
H30	0.130081
H31	0.11118
H32	0.135564
H33	0.00756
H34	0.129428
H35	0.110266
O36	−0.69592
H37	0.349957
H38	0.320227

---

3.8. Molecular electrostatic potential

Molecular electrostatic potential (MEP) at a point in the space around a molecule gives an indication of the net electrostatic effect produced at that point by the total charge distribution of the atom or molecule and correlates with dipole moment, electronegativity, partial charges and chemical reactivity of the molecule. MEP is a well-established powerful tool to elucidate and predict molecular reactive behavior. The different values of the electrostatic potential at the surface are represented by different colors. Potential increases in the order of red < orange < yellow < green < blue. The color code of these maps is in the range between −8.980 × 10⁻² (deepest red) to +8.980 × 10⁻² (deepest blue), more electronegativity appears at the oxygen atoms indicated by yellow color (Fig. 7). The predominance of the light green region over the MEPs surface corresponds to a potential halfway between the two extremes red and dark blue color. Other region appears to be blue color resulting in less electronegativity. The negative regions of were related to electrophilic reactivity and the positive ones to nucleophilic reactivity. As seen from Fig. 7 in IFC, the regions having negative potential are around the oxygen atoms. The electrophiles tend to the negative and the nucleophiles tend to the region of positive MEP. Molecular surfaces obtained by B3LYP level 6-31G(d,p) as the basis set.

Fig. 7 Molecular electrostatic potential of IFC.

3.9. Hirshfeld surfaces

The Hirshfeld surfaces of IFC are displayed in Fig. 8, showing surfaces that have been mapped over a d_norm, shapeindex, curvedness, d_e and d_i. The Hirshfeld surface^47–49 surrounded a molecule is defined by points where the attempt to the electron density from the molecule of interest is equal to the contribution from all the other molecules. For each point on that isosurface two distances are determined: one is d_e represents the distance from the point to the nearest nucleus external to the surface and second one is d_i represents the distance to the nearest nucleus internal to the surface. The normalized contact distance (d_norm) based on both d_e and d_i. The surfaces are shown as transparent to allow visualization of the IFC molecule around which they were calculated. The surface representing the circular depressions (deep red) visible on the Hirshfeld surface indicative of hydrogen bonding contacts and other visible spots are due to O⋯H–C (5.5%), O–H⋯O (10.0%), N–H⋯O (8.4%) and C–H⋯O (7.9%) contacts as shown in Fig. 8a and O⋯H–N (1.3%), O–H⋯O (10.0%) and O⋯H–C (5.5%) contacts are shown in Fig. 8b. The deep red colour spots in d_i (Fig. 8d) are strong interactions such as O–H⋯O (10.0%). The shapeindex (Fig. 8f) surface indicates the electron density surface shape around the molecular interactions. The small range of area and light color on the surface represents a weaker and longer contact other than hydrogen bonds. The curvedness surface (Fig. 8e) indicates the electron density surface curves around the molecular interactions. The two-dimensional fingerprint plots⁵⁰ of IFC exemplify the strong evidence for the intermolecular interactions pattern. In the fingerprint region (Fig. 9), O⋯H (10.0%) interactions are represented by a spike in the bottom area whereas the H⋯O (8.4%) interactions are represented by a spike in the top left region in the fingerprint plot. Hydrogen bonding interactions H⋯H (55.5%) are very high compared to the other bonding interactions. Sharp curved spike at the bottom left area indicates the N⋯H (3.0%) and top left corner with curved spike indicates the H⋯N (1.3%). The finger print at the bottom right area represents C⋯H (7.9%) interactions and top right area represents H⋯C (5.5%) interactions. The finger print at the top right area represents C⋯N and N⋯C (4.7%) interactions. Sharp curved spike at the center area indicates the C⋯C (4.2%) interactions. Relative contributions of various intermolecular interactions in IFC are shown in Fig. S4 (see ESI†). Deformation density is calculated from CrystalExplorer (Version 3.1), using DFT method with 6-31G(d,p) as basis set. The deformation density represents difference between the total electron density of a molecule and the electron density of “neutral spherical unperturbed atoms” superimposed at the same of the molecule. Deformation density clearly explains the surface interaction energy of every atom and bond present in the IFC (Fig. 10). Crystal packing along ‘a’ axis is given in Fig. S5 (see ESI†).

Fig. 8 Hirshfeld surfaces of IFC (a) d_norm (front view) (b) d_norm (back view) (c) d_e (d) d_i (e) curvedness (f) shapeindex.

Fig. 9 Fingerprint plots representing quantity of molecular interactions.

Fig. 10 Deformation density surfaces of IFC.

4. Conclusions

(E)-N′-(4-Isopropylbenzylidene)furan-2-carbohydrazide monohydrate (IFC) single crystals were grown from ethanolic solution and characterized by FT-IR, UV-vis, NMR, GC-mass, elemental, X-ray diffraction and Hirshfeld surface analyses. Optimized geometrical parameters are close to the experimental bond lengths and angles. The TD-SCF calculations lead to a very closer agreement with the experimental absorption spectrum. HOMO and LUMO energies show that charge transfer occurs within the molecule. Electron delocalization is confirmed by MEP, ESP, total density and alpha density maps. The intermolecular charge transfer is evidenced by Mulliken charge population analysis. High first-order molecular hyperpolarizability (β), a superior NLO activity (2.0 times of KDP), high transmittance in the visible region and a small HOMO–LUMO energy gap very much suggest that this hydrazone is a promising NLO material. The analysis of the Hirshfeld surface derived fingerprint plots is shown to be an effective method to identify and quantify various types of intermolecular interactions. Generally, experimental data are well supported by DFT theoretical conclusions.

Acknowledgements

The authors thank the Networking Resource Centre, School of Chemistry, University of Hyderabad, for providing single crystal XRD facility and other characterization studies. One of the authors V. Meenatchi expresses her sincere gratitude to Dr R. Chandrasekar for providing lab facilities in University of Hyderabad. The authors thank the Council of Scientific and Industrial Research (CSIR), New Delhi, for financial support through research grant No. 03(1233)/12/EMR-II, and VM is grateful to CSIR project for the award of SRF (Extended).

References

1. M. Hidai and Y. Mizobe, Chem. Rev., 1995, 95, 1115–1133.
2. D. Enders, L. Wortmann and R. Peters, Acc. Chem. Res., 2000, 33, 157–169.
3. R. Lazny and A. Nodzewska, Chem. Rev., 2010, 110, 1386–1434.
4. S. Kobayashi, Y. Mori, J. S. Fossey and M. M. Salter, Chem. Rev., 2011, 111, 2626–2704.
5. P. Vicini, F. Zani, P. Cozzini and I. Doytchinova, Eur. J. Med. Chem., 2002, 37, 553–564.
6. C. Loncle, J. Brunel, N. Vidal, M. Dherbomez and Y. Letourneux, Eur. J. Med. Chem., 2004, 39, 1067–1071.
7. L. Savini, L. Chiasserini, V. Travagli, C. Pellerano, E. Novellino, S. Cosentino and M. Pisano, Eur. J. Med. Chem., 2004, 39, 113–122.
8. M. Cocco, C. Congiu, V. Lilliu and V. Onnis, Bioorg. Med. Chem., 2006, 14, 366–372.
9. A. Masunari and L. C. Tavares, Bioorg. Med. Chem., 2007, 15, 4229–4236.
10. P. Vicini, M. Incerti, P. La Colla and R. Loddo, Eur. J. Med. Chem., 2009, 44, 1801–1807.
11. J. M. Lehn, Chem. Soc. Rev., 2007, 36, 151–160.
12. J. M. Lehn, in Topics in Current Chemistry, ed. M. Barboiu, Springer, Berlin, 2012, vol. 322, book section Constitutional Dynamic Chemistry: Bridge from Supramolecular Chemistry to Adaptive Chemistry, pp. 1–32.
13. J. M. Lehn, Angew. Chem., Int. Ed., 2013, 52, 2836–2850.
14. R. Lygaitis, V. Getautis and J. V. Grazulevicius, Chem. Soc. Rev., 2008, 37, 770–788.
15. A. Abbotto, L. Beverina, N. Manfredi, G. A. Pagani, G. Archetti, H. G. Kuball, C. Wittenburg, J. Heck and J. Holtmann, Chem.–Eur. J., 2009, 15, 6175–6185.
16. P. Courtot, J. le Saint and R. Pichon, Bull. Soc. Chim. Fr., 1975, 2538–2542.
17. P. Courtot, R. Pichon and J. le Saint, Tetrahedron Lett., 1976, 1181–1184.
18. R. Pichon, J. le Saint and P. Courtot, Tetrahedron, 1981, 37, 1517–1524.
19. X. Su and I. Aprahamian, Chem. Soc. Rev., 2014, 43, 1963–1981.
20. C. Loncle, J. M. Brunel, N. Vidal, M. Dherbomez and Y. Letourneux, Eur. J. Med. Chem., 2004, 39, 1067–1071.
21. S. Papakonstantinou-Garoufalias, N. Pouli, P. Markos and A. Chytyroglou-Ladas, II Farmaco, 2002, 57, 973–977.
22. P. Vicini, F. Zani, P. Cozzini and I. Doytchinova, Eur. J. Med. Chem., 2002, 37, 553–564.
23. B. K. Kaymakcroglu and S. Rollas, II Farmaco, 2002, 57, 595–599.
24. R. Maccari, R. Ottana and M. G. Vigorita, Bioorg. Med. Chem. Lett., 2005, 15, 2509–2513.
25. M. T. Cocco, C. Congiu, V. Onnis, M. C. Pusceddu, M. L. Schivo and A. Logu, Eur. J. Med. Chem., 1999, 34, 1071–1076.
26. D. G. Rando, D. N. Sato, L. Siqueira, A. Malvezzi, C. Q. F. Leite, A. T. Amaral, E. I. Ferreira and L. C. Tavares, Bioorg. Med. Chem., 2002, 10, 557–560.
27. J. Patole, D. Shingnapurkar, S. Padhye and C. Ratledge, Bioorg. Med. Chem. Lett., 2006, 16, 1514–1517.
28. A. Maiti and S. Ghosh, J. Inorg. Biochem., 1989, 36, 131–139.
29. N. Mori, US pat. No. 5, 567, 557, 1996.
30. N. Tatsya and U. Minoru, Japan Patent No. 8, 101, 524, 1996.
31. Y. Suzuki, US Pat. No. 5, 6656, 500, 1997.
32. N. Jurban, Z. Tokarski and T. P. Smith, US Pat. No. 6, 340, 548, 2002.
33. V. Meenatchi, K. Muthu, M. Rajasekar and S. P. Meenakshisundaram, Spectrochim. Acta, Part A, 2014, 124, 423–428.
34. V. Meenatchi, K. Muthu, M. Rajasekar and S. P. Meenakshisundaram, Optik, 2014, 125, 4196–4200.
35. V. Meenatchi, K. Muthu, M. Rajasekar, G. Bhagavannarayana and S. P. Meenakshisundaram, Optik, 2014, 125, 4181–4185.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision C.01, Gaussian, Inc., Wallingford CT, 2009.
37. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218.
38. R. Dennington, T. Keith and J. Millam, GaussView, Version 5, Semichem Inc., Shawnee Mission KS, 2009.
39. P. Kubelka and F. Munk, Zeitschrift für technische Physik., 1931, 12, 593–601.
40. B. Brutschy and P. Hobza, Special issue on van der Waals molecules, Chem. Rev., 2000, 100, 3861–3862.
41. E. A. Donley and D. P. Shelton, Chem. Phys. Lett., 1993, 215, 156–162.
42. S. Yokoyama, T. Nakahama, A. Otomo and S. Mashiko, J. Am. Chem. Soc., 2000, 122, 3174–3181.
43. D. M. Burland, Special issue on Optical Nonlinearities in Chemistry, Chem. Rev., 1994, 94, 1–278.
44. A. Frisch, A. B. Nielson and A. J. Holder, GAUSSVIEW User Manual, Gaussian Inc., Pittsburgh, PA, 2000.
45. D. A. Kleinman, Phys. Rev., 1962, 126, 1977–1979.
46. S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813.
47. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.
48. F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138.
49. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer(Version 3.1), University of Western Australia, 2012.
50. M. A. Spackman and J. J. McKinnon, CrystEngComm, 2002, 4, 378–392.

---

Footnote

† Electronic supplementary information (ESI) available: Supplementary information contains table of FT-IR vibrational modes, NMR, GC-mass and elemental analysis. CCDC 1047261. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c5ra07936e

---