The effect of perpendicular electric field on temperature-induced plasmon excitations for intrinsic silicene

Abstract

We use the tight-binding model and the random-phase approximation to investigate the intrinsic plasmon in silicene. At finite temperatures, an undamped plasmon is generated from the interplay between the intraband and the interband-gap transitions. The extent of the plasmon existence range in terms of momentum and temperature, which is dependent on the size of the single-particle-excitation gap, is further tuned by applying a perpendicular electric field. The plasmon becomes damped in the interband-excitation region. A low damped zone is created by the field-induced spin split. The field-dependent plasmon spectrum shows a strong tunability in the plasmon intensity and spectral bandwidth. This could make silicene a very suitable candidate for plasmonic applications.

---

I. Introduction

A carbon nanosheet, namely graphene, was discovered a few years ago. Its unique low-lying linear energy dispersions have provided researchers with an abundance of new physics, including the Klein paradox for tunneling through a rectangular electrostatic potential barrier,^1–3 the anomalous quantum Hall effect,^4,5 and peculiar optical properties.^6–10 Following the successes achieved with graphene, researchers have intensified their search for other graphene-like two-dimensional materials.^11–13 In recent years, silicene, a nanosheet consisting of silicon atoms, has been synthesized.^14–16 Belonging to the same group as graphene in the periodic table, silicene is predicted to exhibit feature-rich electronic properties. Furthermore, it could be better suited for practical applications than graphene for two main reasons. The first is its compatibility with current Si-based device technologies. The second is its sizable energy gap, owing to the larger magnitude of its atomic spin–orbit interaction (SOI) and its buckled structure. The buckling means that the two sublattices are separated by a vertical distance of 2l (≈0.46 Å), which is a result of the larger ionic size of silicon atoms compared to carbon atoms. Other group-IV elements, e.g., Ge and Sn, are also expected to appear in this form in their 2D structures.^17,18

The out-of-plane buckling suggests that an on-site potential difference between the A and B sublattices is tunable under a perpendicular electric field.^19,20 This allows for the control of the band gap, along with the spin and valley polarized states. Accordingly, many spin and valleytronics, like the quantum spin Hall effect^21–23 and the optically-generated spin-valley-polarized charge carriers,^24–27 may be investigated. Additionally, when the electric potential exceeds the magnitude of the SOI, 2D silicene is predicted to undergo a topological phase transition from a topological insulator to a band insulator, a property that should be important in electronics and optics.

Collective-Coulomb excitations, dominated by electron–electron interactions, are useful for understanding the behavior of electrons in a material, due to the involvement of screening effects. This basic property has been widely studied in various low-dimensional systems, e.g., carbon nanotubes,^28–30 graphene layers,^31–37 and other novel materials.^38–40 In monolayer graphene, plasmons (quantized collective-excitation modes) hardly exist at low frequencies due to the lack of free carriers. This may be improved by doping or insertion of a gate to increase the free-charge density,^41,42 i.e., changing the Fermi level in an extrinsic condition. Alternatively, an intrinsic low-frequency plasmon (with zero Fermi energy) may be induced by increasing the thermally excited electrons and holes in the conduction and valence bands.⁴³ This is based on the strong dependence of the carrier density on the temperature (n ∝ T²). A temperature-induced plasmon is also predicted to exist in monolayer silicene.⁴⁴ The difference is that the temperature-induced plasmon in graphene is always located in the interband region and suffers the Landau damping.⁴³ However, in silicene, the temperature-induced plasmon could be in a single-particle-excitation (SPE) gap arising from the spin–orbit interaction.⁴⁴ The opening of the SPE gap makes the plasmon undamped. In this paper, we investigate the effects of a perpendicular electric field on the T-induced plasmon in silicene. The energy-loss function is used to derive the plasmon spectrum. Three plasmon modes with distinct degrees of Landau damping are found in different momentum, temperature, and field strength ranges. The occurrences of the plasmons and their discontinuous dispersions are associated with special structures in the dielectric functions.

II. Methods

Similar to graphene, silicene consists of a honeycomb lattice of silicon atoms with two sublattices made up of A and B sites. The difference is that silicene has a buckled structure, with the two sublattice planes separated by a distance of 2l with l = 0.23 Å (Fig. 1). In the tight-binding approximation, the Hamiltonian for silicene in the presence of SOI is written as:^18,45where c^†_iα (c_jβ) creates (annihilates) an electron with spin polarization α(β) at site i(j). The sum is taken over all pairs of nearest neighbors 〈i,j〉 or next-nearest-neighbor ⟪i, j⟫ lattice sites. The first term in eqn (1) is the usual nearest-neighbor hopping integral with a transfer energy of t = 1.6 eV. The second term describes the effective SO coupling with λ_SO = 3.9 meV. [small sigma, Greek, vector] = (σ_x,σ_y,σ_z) is the vector of the Pauli matrices. v_ij is determined by the orientation of the two nearest bonds connecting the next-nearest neighbors, i.e., v_ij = +1(−1) if the next-nearest-neighbor hopping is anticlockwise (clockwise) with respect to the positive z axis. The third term is the intrinsic Rashba SO coupling with λ_R2 = 0.7 meV, where with 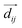connecting two sites i and j in the same sublattice, and u_ij = ±1 represents the A(B) site. The fourth term is the staggered sublattice potential energy produced by the external electric field, where μ_i = ±1 for the A(B) site. The tight-binding Hamiltonian can also be used to describe other group-IV elements, such as germanium with a different set of parameters (t = 1.3 eV, λ_SO = 43 meV, λ_R2 = 10.7 meV, and l = 0.33 Å in the case of Ge¹⁸).

Fig. 1 The lattice geometry of low-buckled silicene. The two sublattices are separated by a perpendicular distance of 2l. The staggered sublattice potential energy is produced by an external electric field E_z.

When the system is perturbed by a time-dependent Coulomb potential, the electron–electron interactions would induce a charge density fluctuation which acts to screen the external perturbation. This dielectric screening determines the normal modes of the charge density oscillations. Electronic excitations are characterized by the transferred momentum q and the excitation frequency ω, which determine the dielectric function. Within the random-phase approximation, the dielectric function can be expressed as:

ε(q,ω) = ε₀ − v_qχ⁰(q,ω), (2)

where v_q = 2πe²/q is the in-plane Fourier transformation of the bare Coulomb potential energy, and ε₀ = 2.4 (taken from graphite⁴⁶) is the background dielectric constant due to deep-energy electronic states. It is noted that changing ε₀ would cause a vertical shift of the real part of the dielectric function (Fig. 3) and thus change the peak intensity and position in the energy loss function (Fig. 4). However, the plasmon behavior is qualitatively the same (Fig. 5). Such a form of the dielectric function is utilized in many researches on two-dimensional systems, theoretically^31,47,48 and experimentally.^49–51 The bare response function χ⁰ is given by:^46,52

Fig. 2 The low-energy bands of monolayer silicene in the presence of spin–orbit coupling about the K point are shown in (a). Those under E_z = 0.5E_c, E_c, and 2E_c are shown in (b), (c), and (d), respectively.

Fig. 3 The dielectric function as a function of ω at q = 1 and T = 0 is shown in (a). Those for T = 50 K and different E_z values are shown in (b)–(e). The purple and orange curves represent the real and the imaginary parts, respectively. The energy broadening width is Γ = 0.1 meV. q is in units of 10⁵ cm⁻¹.

Fig. 4 The energy-loss functions for fixed q = 1, T = 50 K, and different E_z values are plotted in (a)–(d). Those for E_z = 0 and E_z = 0.5E_c at T = 0 are plotted in the insets of (a) and (b), respectively.

Fig. 5 The q-dependent plasmon spectrum at T = 50 K for (a) E_z = 0, (b) E_z = 0.5E_c, (c) E_z = E_c, and (d) E_z = 2E_c. The dashed blue and white curves in each panel indicate the interband and intraband SPE boundaries, respectively. The color scale stands for the values of the energy-loss function.

Each Bloch state is labeled by the Bloch wave vector k and the band index n. Eⁿ is the corresponding eigenvalue. The Fermi-Dirac distribution is f(Eⁿ) = 1/{1 + exp[(Eⁿ − μ)/k_BT], where k_B is the Boltzmann constant and μ is the chemical potential. μ is set to zero over the range of the symmetric conduction (c) and valence (v) bands under investigation. Γ is the energy broadening which results from various de-excitation mechanisms, e.g., the optical transitions between the valence- and conduction-band states. It is usually set low in the low-frequency region. Changing Γ would not alter the peak positions in the energy-loss function (Fig. 4), but the peak intensities and widths would be affected.

The details of the calculation of the Coulomb matrix elements are shown below.

τ₁ and τ₂ define the positions of atoms in a unit cell. u_nsi(k⃑)(u_n′si(k⃑ + q⃑)) are the coefficients for the TB wavefunctions derived from eqn (1). 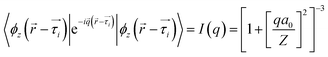was calculated using the hydrogenic wavefunction,⁴⁶ where a₀ is the Bohr radius and Z is the effective core charge.⁵³ For small q values, I(q) is very close to 1. The double integral is performed numerically with respect to the wave vector and band index.

III. Results and discussion

The Hamiltonian of eqn (1) is solved numerically to derive the whole π-band structure and the coefficients for the TB wave functions. The low-energy band structure around the K point in the 1st Brillouin zone is presented in Fig. 2. In this region, the energy dispersion can be described by the Dirac theory.⁵⁴ At zero fields (Fig. 2(a)), all energy bands are spin degenerate. The main effect of the SOI is to produce a small energy gap E_g between the valence and conduction bands. When a perpendicular electric field E_z is applied, each band exhibits spin-split sub-bands due to the breaking of the inversion symmetry (Fig. 2(b)–(d)). Consequently, the system is characterized by two energy gaps, E_1g and E_2g for spin-down (blue curve) and spin-up (red curve) sub-bands, respectively. The former decreases with increasing field strength, while the opposite is true for the latter. The spin-down and spin-up sub-bands are reversed at different valleys. Whenever E_z = E_c (≈λ_SO/l = 17 meV Å⁻¹), the staggered sublattice potential energy exactly compensates for the SOI on the spin-down states and the gap of E_1g is closed (Fig. 2(c)). Meanwhile, the spin-split energy at the K point reaches its maximum, i.e., 2λ_SO. For E_z > E_c (Fig. 2(d)), E_1g is reopened, and the system is transformed into a band insulator. After that, both E_1g and E_2g increase with E_z, while the spin-split energy at the K point remains constant at 2λ_SO.

The unscreened-excitation spectrum is helpful in understanding the single-particle excitation (SPE) channels. At zero temperature (Fig. 3(a)), the interband excitations are the only available excitation channel. The threshold excitation energy is expressed as . The real (ε₁) and imaginary (ε₂) parts of the longitudinal dielectric function, related through the Kramers–Kronig relationship, exhibit a logarithmic-divergent peak and a step-like structure at ω^inter_th, respectively. The interband-gap transitions account for these prominent structures. There are no zero points in ε₁. That is, for T = 0, no self-sustained plasmon excitations can exist in the low-frequency region. The intraband transitions are allowed at finite temperatures; these transitions create additional special structures in ε, i.e., an asymmetric dip and peak in ε₁ and ε₂, respectively, as illustrated in Fig. 3(b) for T = 50 K. At the same time, the interband-transition-related structures become weaker. The highest intraband-excitation energy is ω^intra_ex = v_Fq, which is lower than ω^inter_th. Therefore, a SPE gap is developed in ε₂. The asymmetric dip in ε₁ creates two zero points. One of the zero points is located in the ε₂ gap (only for the condition k_BT < E_g), where an undamped plasmon mode can occur. The temperature range that allows the undamped plasmon depends on the width of the SPE gap; this width is tunable by an external E-field.

The effects of the E-field on ε are displayed in Fig. 3(c)–(e) for fixed temperature of T = 50 K and different E_z values. At E_z = 0.5E_c, shown in Fig. 3(c), the step structure (peak) in ε₂(ε₁) is split into two owing to the lifting of the spin degeneracy, as indicated by the pair of blue arrows. The two steps of the structure develop at ω^inter_1,th and ω^inter_2,th. Between ω^inter_1,th and ω^inter_2,th the density of the e–h pairs is half of that beyond ω^inter_2,th. This means the creation of a low-damped plasmon region. ω^inter_1,th decreases when E_z is increased from zero to E_c, i.e., the SPE gap is reduced. This may hinder the occurrence of an undamped plasmon. The opposite is true for E_z > E_c (Fig. 3(e)). At E_z > E_c (Fig. 3(d)), ω^inter_1,th and ω^intra_ex merge. Therefore, both zero points of ε₁ are located where ε₂ is finite. Under such conditions, only damped plasmons can exist.

The energy-loss function (∝Im[−1/ε]), related to the screened excitation spectrum, is used to understand the collective-excitation mode of the electrons. The quantity can be measured from electron energy loss spectroscopy in transmission^50,51,55,56 and reflection modes,⁵⁷ and inelastic light scattering.⁵⁸ Each prominent structure in Im[−1/ε] may be viewed as a plasmon excitation with different degrees of Landau damping. At T = 0, the low-frequency Im[−1/ε] appears as plateaus without and with an electric field, as shown in the insets of Fig. 4(a) and (b), respectively. The featureless plateau structures correspond to the interband excitations, which exhibit single-particle like behaviors. At finite temperatures, a prominent peak is induced with a frequency lower than the plateaus (Fig. 4(a)–(d) for T = 50 K). The corresponding dielectric functions reveal that this peak could arise from the interplay between the intraband and interband-gap transitions (Fig. 3(b), (c) and (e)) or merely from the sufficiently strong intraband transitions under the condition of a zero SPE gap (Fig. 3(d)). The former leads to a stronger peak intensity and a narrower peak width in the energy-loss function (Fig. 4(a), (b) and (d)), compared with that caused by the latter (Fig. 4(c)).

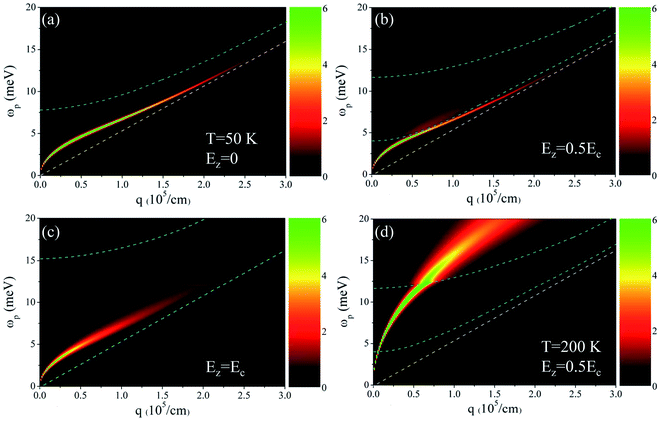
The q-dependent behavior of plasmons is important in understanding their characteristics. Fig. 5(a)–(c) show the results for different E_z values at a fixed temperature of T = 50 K. The color scale stands for the values of the energy-loss function. The dashed curves in each figure represent the highest intraband (white curves) and the lowest interband (blue curves) SPE energies, which obey the relationship ω = v_Fq and 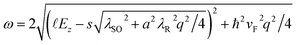with s = ±1, respectively. The expressions are derived from the analytical solution of the single-particle spectrum near the K point.⁵⁴ These boundary curves define the various regions with different degrees of Landau damping. Between the white and the blue boundary curves lies the SPE gap, where an undamped plasmon branch exists. The plasmon frequency ω_p is well fitted by in the long-wavelength limit, a feature of a 2D plasmon. For lower temperatures (Fig. 5(a) and (b)), this plasmon mode is finally damped out in the intraband SPE continuum at larger q values. The existence range of the undamped plasmon in momentum is proportional to the width of the SPE gap, which is reduced in the region of 0 < E_z < E_c (Fig. 5(b) for E_z = 0.5E_c). There are two blue boundary curves in E_z ≠ 0 (Fig. 5(b)–(d)). They are the result of the lifting of the spin degeneracy. Between the two blue curves lies a low damped region. In Fig. 5(b), a broad plasmon branch appears in the region, just above the undamped plasmon mode. The coexistence of the two collective-excitation modes can only be realized at k_BT ≈ E_1g. The SPE gap is closed at E_z = E_c (Fig. 5(c)). Then, the plasmon is damped at arbitrary q values. Until E_z > E_c, the undamped plasmon branch is regained (not shown). Under the above conditions, the plasmon dispersion is confined between two SPE boundary curves. However, when the temperature is sufficiently high, e.g., T = 200 K and E_z = 0.5E_c in Fig. 5(d), the plasmon branch crosses the SPE boundaries and shows abrupt changes in intensity and bandwidth. The discontinuous plasmon dispersion is more evident when the plasmon crosses the upper blue curve. After that, the plasmon enters the strong damped region. It is worth noting that the temperature-induced plasmon differs from the extrinsic plasmon discussed in doped silicene.⁵⁹ The dispersion relationship of the extrinsic plasmon is decided by the Fermi energy. This is in great contrast to the intrinsic plasmon whose dispersion is dominated by the temperature. The different electron distributions result in different plasmon dispersions between the two conditions.

The effect of temperature variation on the plasmon excitation is worth further discussion. Fig. 6(a)–(c) show the T-dependent plasmon spectra at fixed q = 1 and different E_z values. The distribution range of the undamped plasmon mode (between the blue and white dashed curves) with T is reduced in the region of 0 < E_z < E_c (Fig. 6(b) for E_z = 0.5E_c) and diminished to zero at E_z = E_c (Fig. 6(c)), compared to the condition of E_z = 0 (Fig. 6(a)). The undamped plasmon is transformed to a damped one above a critical temperature (T_c ≃ 100 K for E_z = 0). The transformation in the plasmon mode during the change in T is a discontinuous process, a feature that could allow for the identification of the spin–orbit energy gap. The discontinuous dispersions of the plasmons remain when changing the background dielectric constant ε₀ and energy broadening Γ. In Fig. 6(b) for E_z = 0.5E_c, two critical temperatures exist through which the plasmon spectrum is drastically altered. The two T_c values correspond to the two energy gaps opening in the system. This could be used to examine the spin degeneracy and determine E_c. Note that above the highest T_c value (≈175 K for E_z = 0.5E_c), the plasmon intensity grows monotonically with T, similar to the behavior of the intrinsic plasmon in gapless graphene.⁴³ This indicates that at such high temperatures the SOI effect becomes negligible.

Fig. 6 The T-dependent plasmon spectrum at fixed q = 1 and different E_z values: (a) E_z = 0, (b) E_z = 0.5E_c, and (c) E_z = E_c. The blue and white dashed curves in each panel indicate the interband and intraband SPE boundaries, respectively. The color scale stands for the values of the energy-loss function.

For fixed q and T, the plasmon existence and its spectral weight can be effectively controlled by varying E_z, as shown in Fig. 7. At T = 50 K and q = 1 (Fig. 7(a)), the undamped plasmon is stable for E_z < 0.5E_c due to the significantly large SPE gap. When E_z is increased to near E_c, the plasmon is damped by the interband SPEs and fades. The SPE gap is reopened in the region of E_z > E_c. After that the plasmon is intensified first with the increment of E_z, and when E_z exceeds another critical value E′_c (E′_c ≈ 3E_c for T = 50 K and q = 1), the plasmon is gradually damped out in the intraband SPE continuum. At T = 100 K (Fig. 7(b)), the undamped plasmon barely exists in E_z < 2E_c, because the overly strong intraband transitions make the plasmon frequency higher than the threshold interband SPE energy. Until E_z > 2E_c, the energy gap becomes larger than k_BT, and the undamped plasmon emerges. The undamped plasmon at T = 100 K can survive in a larger E_z than that at T = 50 K. The stronger intraband transitions can explain this. At T = 200 K (Fig. 7(c)), the plasmon spectrum displays three distinct degrees of Landau damping in different E_z ranges. In the first region (0 < E_z < 0.7E_c), the plasmon is located beyond the two interband SPE boundaries and suffers strong Landau damping. In the second region (0.7E_c < E_z < 2.5E_c), the plasmon lies between the two interband boundaries and is weakly damped. In the third region (E_z > 2.5E_c), the plasmon lies inside the SPE gap and is undamped. Though the plasmon intensity strongly depends on E_z, the change in the plasmon frequency is insignificant. This illustrates that the appearance of the low-frequency plasmon is mainly dominated by the intraband transitions.

Fig. 7 The E_z-dependent plasmon spectrum at fixed q = 1 and different T values: (a) T = 50 K, (b) T = 100 K, and (c) T = 200 K. The color scale stands for the values of the energy-loss function.

IV. Summary and conclusions

The Coulomb-excitation properties of silicene were studied by the tight-binding model and random-phase approximation. The temperature and E-field effects were considered simultaneously. At finite temperatures, an undamped plasmon is induced by the interplay between the intraband and interband-gap transitions. The plasmon mode only exists in a limited region of T and q, which can be further tuned by varying E_z. Thanks to the opening of two energy gaps from the spin split in E_z, there are three distinct degrees of Landau damping in different q, T, and E_z ranges. Therefore, the plasmon dispersion is discontinuous at certain critical q and T values. The phenomenon could be used to identify the spin degeneracy and to determine relevant theoretical parameters, such as the magnitude of SOI. We further show that, for a given q and T, changing E_z can control the plasmon intensity and its existence at a nearly fixed frequency, a property that should be important in plasmonic applications. Tunable low-frequency plasmons can also potentially be found in other 2D structures with band gaps that can be adjusted by an external E-field, e.g., germanene and stanene.

Acknowledgements

This work was supported by the NSC of Taiwan, under Grant no. NSC 102-2112-M-006-007-MY3.

References

1. M. I. Katsnelson, K. S. Novoselov and A. K. Geim, Nat. Phys., 2006, 2, 620.
2. C. Bai and X. D. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 075430.
3. A. F. Young and P. Kim, Nat. Phys., 2009, 5, 222.
4. Y. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
5. E. McCann and V. I. Fal’ko, Phys. Rev. Lett., 2006, 96, 086805.
6. D. S. L. Abergel and V. I. Falko, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155430.
7. R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres and A. K. Geim, Science, 2008, 320, 1308.
8. F. Bonaccorso, Z. Sun, T. Hasan and A. C. Ferrari, Nat. Photonics, 2010, 4, 611.
9. Y. H. Ho, Y. H. Chiu, D. H. Lin, C. P. Chang and M. F. Lin, ACS Nano, 2010, 4, 1465.
10. Z. Zheng, C. Zhao, S. Lu, Y. Chen, Y. Li, H. Zhang and S. Wen, Opt. Express, 2012, 20, 23201.
11. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699.
12. M. Xu, T. Liang, M. Shi and H. Chen, Chem. Rev., 2013, 113, 3766.
13. S. Z. Butler, et al., ACS Nano, 2013, 7, 2898.
14. P. Vogt, P. D. Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. L. Lay, Phys. Rev. Lett., 2012, 108, 155501.
15. L. Chen, C. C. Liu, B. Feng, X. He, P. Cheng, Z. Ding, S. Meng, Y. Yao and K. Wu, Phys. Rev. Lett., 2012, 109, 056804.
16. Z. L. Liu, M. X. Wang, J. P. Xu, J. F. Ge, G. L. Lay, P. Vogt, D. Qian, C. L. Gao, C. Liu and J. F. Jia, New J. Phys., 2014, 16, 075006.
17. K. Takeda and K. Shiraishi, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 14916.
18. C. C. Liu, H. Jiang and Y. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 195430.
19. Z. Ni, Q. Liu, K. Tang, J. Zheng, J. Zhou, R. Qin, Z. Gao, D. Yu and J. Lu, Nano Lett., 2012, 12, 113.
20. C. Lian and J. Ni, Phys. Chem. Chem. Phys., 2015, 17, 13366.
21. C. J. Tabert and E. J. Nicol, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 235426.
22. C. C. Liu, W. Feng and Y. Yao, Phys. Rev. Lett., 2011, 107, 076802.
23. M. Tahir and U. Schwingenschlögl, Sci. Rep., 2013, 3, 1075.
24. M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 161407(R).
25. L. Stille, C. J. Tabert and E. J. Nicol, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195405.
26. C. J. Tabert and E. J. Nicol, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085434.
27. C. J. Tabert and E. J. Nicol, Phys. Rev. Lett., 2013, 110, 197402.
28. M. F. Lin and K. W.-K. Shung, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17744.
29. M. F. Lin, D. S. Chuu and K. W.-K. Shung, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 1430.
30. S. Dmitrović, T. Vuković, B. Nikolić, M. Damnjanović and I. Milošević, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 245415.
31. J. Y. Wu, S. C. Chen, O. Roslyak, G. Gumbs and M. F. Lin, ACS Nano, 2011, 5, 1026.
32. M. F. Lin, Y. C. Chuang and J. Y. Wu, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125434.
33. Y. C. Chuang, J. Y. Wu and M. F. Lin, Sci. Rep., 2013, 3, 1368.
34. J. Y. Wu, G. Gumbs and M. F. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 165407.
35. X. Luo, T. Qiu, W. Lu and Z. Ni, Mater. Sci. Eng., R, 2013, 74, 351.
36. F. Javier Garcia de Abajo, ACS Photonics, 2014, 1, 135.
37. A. N. Grigorenko, M. Polini and K. S. Novoselov, Nat. Photonics, 2012, 6, 749.
38. A. Scholz, T. Stauber and J. Schliemann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 035135.
39. T. Stauber, J. Phys.: Condens. Matter, 2014, 26, 123201.
40. P. Di Pietro, M. Ortolani, O. Limaj, A. Di Gaspare, V. Giliberti, F. Giorgianni, M. Brahlek, N. Bansal, N. Koirala, S. Oh, P. Calvani and S. Lupi, Nat. Nanotechnol., 2013, 8, 556.
41. B. Wunsch, T. Stauber, F. Sols and F. Guinea, New J. Phys., 2006, 8, 318.
42. C. W. Chiu, S. H. Lee, S. C. Chen and M. F. Lin, J. Appl. Phys., 2009, 106, 113711.
43. M. F. Lin and F. L. Shyu, J. Phys. Soc. Jpn., 2000, 69, 607.
44. J. Y. Wu, S. C. Chen and M. F. Lin, New J. Phys., 2014, 16, 125002.
45. M. Ezawa, Phys. Rev. Lett., 2012, 109, 055502.
46. K. W. K. Shung, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 34, 979.
47. S. Yuan, R. Roldan and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035439.
48. M. Pisarra, A. Sindona, P. Riccardi, V. M. Silkin and J. M. Pitarke, New J. Phys., 2014, 16, 083003.
49. S. Y. Shin, C. G. Hwang, S. J. Sung, N. D. Kim, H. S. Kim and J. W. Chung, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 161403(R).
50. T. Eberlein, U. Bangert, R. R. Nair, R. Jones, M. Gass, A. L. Bleloch, K. S. Novoselov, A. Geim and P. R. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 233406.
51. C. Kramberger, R. Hambach, C. Giorgetti, M. H. Rummeli, M. Knupfer, J. Fink, B. Buchner, L. Reining, E. Einarsson, S. Maruyama, F. Sottile, K. Hannewald, V. Olevano, A. G. Marinopoulos and T. Pichler, Phys. Rev. Lett., 2008, 100, 196803.
52. H. Ehrenreich and M. H. Cohen, Phys. Rev., 1959, 115, 786.
53. C. Zener, Phys. Rev., 1930, 36, 51.
54. M. Ezawa, New J. Phys., 2012, 14, 033003.
55. P. Wachsmuth, R. Hambach, M. K. Kinyanjui, M. Guzzo, G. Benner and U. Kaiser, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 075433.
56. C. T. Pan, R. R. Nair, U. Bangert, Q. Ramasse, R. Jalil, R. Zan, C. R. Seabourne and A. J. Scott, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 045440.
57. T. Langer, H. Pfnur, H. W. Schumacher and C. Tegenkamp, Appl. Phys. Lett., 2009, 94, 112106.
58. D. Richards, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 7517.
59. H. R. Chang, J. Zhou, H. Zhang and Y. Yao, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 201411.

---