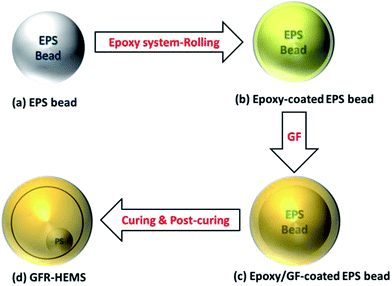
A “rolling ball method” to make glass fiber reinforced hollow epoxy macrospheres used for a three phase epoxy syntactic foam
X. F. Wu*ab,
Y. Wangc,
X. R. Yangc,
J. H. Yuc,
L. C. Wangc,
S. J. Houc and
P. K. Jiangc
aCollege of Ocean Science and Engineering, Shanghai Maritime University, Shanghai, 201306, China. E-mail: coolwu1234@163.com
bState Key Laboratory for Modification of Chemical Fibers and Polymer Materials, Donghua University, Shanghai, 201620, China
cShanghai Key Lab of Electrical Insulation and Thermal Aging, Department of Polymer Science and Engineering, Shanghai Jiao Tong University, Shanghai, 200240, China
First published on 30th June 2015
Abstract
Glass fiber reinforced hollow epoxy macrospheres (GFR-HEMS) and hollow glass microspheres (HGMS) were used to prepare a three phase epoxy syntactic foam (ESF) in this study. An innovative “rolling ball method” was implemented in the preparation of GFR-HEMS where expanded polystyrene (EPS) beads were used as an initiation template. The EPS beads were coated with the epoxy resin and glass fiber using the “rolling ball method”, and these coated EPS beads were later cured and post-cured at high temperature which caused the EPS beads to shrink thus producing a hollow macrosphere structure. The effects of the volume fraction of the GFR-HMES, the wall thickness of the GFR-HEMS and the volume fraction of the HGMS on the compressive properties were discussed to find a comprehensive understanding of the structure–property relationship between the epoxy matrix and sphere fillers. Scanning electron microscopy (SEM) shows that the “rolling ball method” can make glass fibers form a fiber spherical x–y network throughout the macrosphere wall, which can make the GFR-HEMS and three phase ESF have great compressive strength. The ESF (570 kg m−3, 27.3 MPa) can withstand 2730 meters water pressure and provide 430 kg m−3 buoyancy, which can give some advice to the preparation of buoyancy material used in deepwater oil exploration.
1. Introduction
Low density materials with high compressive strength and tolerance are often used as core materials in sandwich composites for aerospace, automotive, civil as well as marine structural applications.1 Especially in the area of marine structural applications, the low density buoyancy materials are used to balance gravity and the buoyancy of the oilfield drilling pipe. In 1000 meters deepwater, the water pressure is about 100 atmospheres, about 100 kgf cm−2. The buoyancy material needs to withstand the enormous pressure of the water while providing sufficient buoyancy. So the higher the hydrostatic pressure resistance and the lower the density of the buoyancy material, the better the performance of the buoyancy material.Buoyancy materials can be classified as a one phase foam, a two phase foam or a three phase foam. A one phase foam is mainly a polymer foam such as PS foam and PU foam, but the foams have limitations because of their low compressive strength,2 so a class of closed cell syntactic foams were introduced by dispersing rigid hollow particles in a matrix.3–5 A two phase foam consists of hollow spheres dispersed in a matrix resin whereas a three phase foam consists of hollow spheres dispersed in a matrix resin containing gaseous voids or other hollow spheres.6–9
Most microspheres are made from rigid shell materials such as polymeric materials, ceramic and glass.10–25 Polymeric microspheres have limitations because of their low compressive strength (<10 MPa). Ceramic microspheres have limitations because of their high density (>0.6 g cm−3). HGMS (Ø 10–150 μm) have the required collapse pressure and density (20–40 MPa, 300–500 kg m−3) and have actually been used in an epoxy/HGMS buoyancy material.26 The density of the foam filled with only HGMS can be calculated by the following formula (1).
| ρfoam =ΦρHGMS + (1 − Φ)ρmatrix | (1) |
Most studies on the mechanical and fracture properties of syntactic foams are based on the maximum filler content of the microspheres as this elicits the lowest possible weight of the composites.30–33 In this study, innovative centimeter-sized GFR-HEMS with low density and high compressive strength were prepared using a “rolling ball method” and used as second reinforcing sphere fillers to prepare a three phase ESF used in deepwater buoyancy products. These materials were combined together using a simple casting technique. Thus it provides a different approach in the production of a syntactic foam compared to previously studied foams.34–36 Centimeter-sized GFR-HEMS could further reduce the density of the syntactic foam on the basis of the epoxy/HGMS composite. The macrosphere preparation method often is the secret of the marine equipment production company. Samsudin37 prepared epoxy hollow spheres using a CaCO3 powder to ensure that the stickiness problem of the uncured epoxy-coated beads was addressed, thus preventing the beads from clumping to each other. The “rolling ball method” in this paper can prepare GFR-HEMS automatically using a rolling ball machine and glass fiber was added into the epoxy hollow sphere to improve the compressive strength of the GFR-HEMS. The “rolling ball method” is improved on the basis of the Samsudin method.37
The study also investigates the influence of different compositions of syntactic foam on its mechanical properties. A comprehensive understanding of the structure–property relationship is lacking. Different compositions will be created by varying the types (GFR-HMES and HGMS) and volume fraction of microspheres or macrospheres. In the three phase ESF, the effects of the volume fraction of the GFR-HMES, the wall thickness of the GFR-HEMS and the volume fraction of the HGMS on the compressive properties were discussed. It is expected that the interfacial adhesion between the spheres (HGMS and GFR-HEMS) and the epoxy matrix could be stronger. It is also expected that the GFR-HEMS and HGMS could coordinate to improve the comprehensive performance of the three phase ESF.
2. Experimental
2.1 Materials
The resin used in this paper was a Huntsman 1564/3486 epoxy resin system. The Huntsman Araldite® LY 1564 was a modified bisphenol-A type epoxy resin and the hardener Aradur® 3486 was a polyamine curing agent. It was manufactured by the Huntsman Products Inc, USA. The epoxy resin 1564 was a clear liquid, and the curing agent 3486 was a clear colourless to a slightly yellow liquid. The mix ratio was 1564![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3486 = 100
3486 = 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 34 by weight. 1564 had the following characteristics: viscosity in the range of 1200–1400 mPa s (ISO 12058-1) and density of 1.1–1.2 g cm−3 at 25 °C (ISO 1675), epoxy index (ISO 3001) was 5.8–6.05 eq. kg−1. 1564 resin was chosen as the polymer matrix for the syntactic foam due to the wide variety of curing agents available to cure the liquid epoxy resin at ambient conditions. The characteristics of 3486 curing agent were: viscosity (ISO 12058-1) in the range of 10–20 mPa s and specific gravity (ISO 1675) of 0.94–0.95 g cm−3 at 25 °C, amine value (ISO 9702) was 8.55–9.30 eq. kg−1. Initial mix viscosity (Hoeppler, ISO 12058-1B) LY 1564/Aradur® 3486 at 25 °C was 200–300 mPa s, Pot life (Tecam, 23 °C, 65% RH) of LY 1564/Aradur® 3486 (100 g) was 560–620 min, gel life (hot plate) of LY 1564/Aradur® 3486 at 60 °C was about 110–130 min. So the LY 1564/Aradur® 3486 system provided a reasonably good curing process at ambient temperature.
34 by weight. 1564 had the following characteristics: viscosity in the range of 1200–1400 mPa s (ISO 12058-1) and density of 1.1–1.2 g cm−3 at 25 °C (ISO 1675), epoxy index (ISO 3001) was 5.8–6.05 eq. kg−1. 1564 resin was chosen as the polymer matrix for the syntactic foam due to the wide variety of curing agents available to cure the liquid epoxy resin at ambient conditions. The characteristics of 3486 curing agent were: viscosity (ISO 12058-1) in the range of 10–20 mPa s and specific gravity (ISO 1675) of 0.94–0.95 g cm−3 at 25 °C, amine value (ISO 9702) was 8.55–9.30 eq. kg−1. Initial mix viscosity (Hoeppler, ISO 12058-1B) LY 1564/Aradur® 3486 at 25 °C was 200–300 mPa s, Pot life (Tecam, 23 °C, 65% RH) of LY 1564/Aradur® 3486 (100 g) was 560–620 min, gel life (hot plate) of LY 1564/Aradur® 3486 at 60 °C was about 110–130 min. So the LY 1564/Aradur® 3486 system provided a reasonably good curing process at ambient temperature.
HGMS (S38HS) was obtained from the 3M company (Minnesota Mining and Manufacturing, USA) with a different range of sizes (about 15–85 μm). The real density and compressive strength were 0.38 g cm−3 and 37.9 MPa, respectively. The EPS beads were supplied by Shanghai Qiyuan Packaging Technology Co., Ltd (Shanghai, China) with a different range of sizes (9–10 mm, 10 kg m−3) and were used as intermediate materials to develop the GFR-HEMS. The glass fiber powder was supplied by Hangzhou High-tech composite company, China. The size of glass fiber powder was about 300 mesh, the diameter was about 9 micrometers, the length was about 30–50 micrometers, the density was about 2.54 g cm−3.
2.2 Preparation of the GFR-HEMS
The GFR-HEMS were prepared by a “rolling ball method”. The preparation process of the GFR-HEMS is described by Fig. 1 and 2. Fig. 1 shows the schematic process of glass fiber reinforcing the epoxy-coated EPS beads. Fig. 2 shows the preparation process of the GFR-HEMS.A resin mixture comprising of the clear epoxy resin (Araldite® LY 1564) and polyamine hardener (Aradur® 3486) with a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio was formulated and mixed using a Planetary Centrifugal Mixer (THINKY Mixer ARE-310, Japan) to produce the epoxy system uniformly without air bubbles. The EPS beads (Fig. 2(a)) were later added into the prepared epoxy system in apportioned quantities and were ensured to be fully coated by the epoxy system. These beads were used as intermediate materials to develop the GFR-HEMS. After that, the epoxy-coated EPS beads (Fig. 2(b)) were transferred into a tumbler (shown in Fig. 1). Then a sufficient amount of glass fiber powder (about 10 times the mass of the epoxy–hardener system) was injected into the tumbler from spout 1 during rotation of the tumbler (shown in Fig. 1). On one hand, his step is to ensure that the stickiness problem of the uncured epoxy-coated beads was addressed, thus preventing the EPS beads from clumping to each other. On the other hand, the addition of glass fiber can also enhance the compressive strength of the epoxy macrospheres after curing. At the same time, the tumbler rotation made the thickness of the epoxy resin on the EPS beads uniform. These EPS beads coated with glass fiber (Fig. 2(c)) were then cured in an oven for 30 minutes at 50 °C and post-cured at 120 °C for 60 minutes (Fig. 2(d)) to shrink all the EPS beads inside the epoxy-coated spheres with the intention of producing hollow structures within the spheres.
1 ratio was formulated and mixed using a Planetary Centrifugal Mixer (THINKY Mixer ARE-310, Japan) to produce the epoxy system uniformly without air bubbles. The EPS beads (Fig. 2(a)) were later added into the prepared epoxy system in apportioned quantities and were ensured to be fully coated by the epoxy system. These beads were used as intermediate materials to develop the GFR-HEMS. After that, the epoxy-coated EPS beads (Fig. 2(b)) were transferred into a tumbler (shown in Fig. 1). Then a sufficient amount of glass fiber powder (about 10 times the mass of the epoxy–hardener system) was injected into the tumbler from spout 1 during rotation of the tumbler (shown in Fig. 1). On one hand, his step is to ensure that the stickiness problem of the uncured epoxy-coated beads was addressed, thus preventing the EPS beads from clumping to each other. On the other hand, the addition of glass fiber can also enhance the compressive strength of the epoxy macrospheres after curing. At the same time, the tumbler rotation made the thickness of the epoxy resin on the EPS beads uniform. These EPS beads coated with glass fiber (Fig. 2(c)) were then cured in an oven for 30 minutes at 50 °C and post-cured at 120 °C for 60 minutes (Fig. 2(d)) to shrink all the EPS beads inside the epoxy-coated spheres with the intention of producing hollow structures within the spheres.
The GFR-HEMS made above can be called 1 layer GFR-HEMS. Increasing the thickness of the GFR-HEMS would affect the mechanical properties of the following three phase ESF. So 2 layer GFR-HEMS and 3 layer GFR-HEMS were also prepared by the above method based on the 1 layer GFR-HEMS, in order to investigate the effect of the GFR-HEMS thickness on the properties of the three phase ESF composite. In the preparation process of the 2 layer GFR-HEMS, the 1 layer GFR-HEMS was used as a template, and the amount of epoxy–hardener–glass fiber was the same as the amount of epoxy–hardener–glass fiber for the 1 layer GFR-HEMS. The 2 layer GFR-HEMS were used as a template in the preparation process of the 3 layer GFR-HEMS.
In the preparation process of the GFR-HEMS, the glass fiber used was sufficient. So the volume fraction of glass fiber almost did not change in the three kinds of GFR-HEMS with different layers. The volume fraction of glass fiber in the GFR-HEMS was about 61.5% ± 2.6% tested by Thermogravimetric Analysis.
2.3 Preparation of the three phase epoxy syntactic foam filled with different stacking volume fractions of the GFR-HEMS
In order to study the influence of the stacking volume fraction of the GFR-HEMS on the compressive strength of the three phase ESF, GFR-HEMS with different stacking volume fractions (100%, 80%, 60%, 40%, 20% and 0%) were added into the two-phase epoxy–HGMS composite to make the three phase ESF. Fig. 3 shows the preparation process of the three phase ESF filled with different stacking volume fractions of the GFR-HEMS.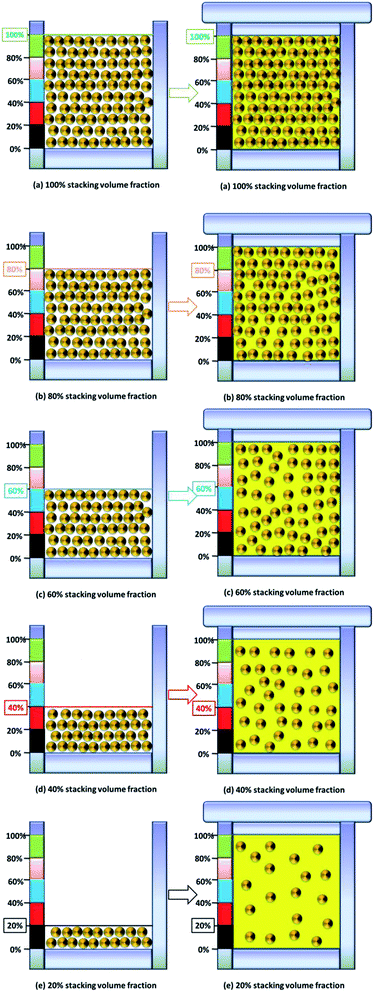 | ||
| Fig. 3 Preparation process of the three phase ESF filled with different stacking volume fractions of the GFR-HEMS. | ||
The preparation involves determining the amount of GFR-HEMS needed in the next experimental procedure by filling a stainless steel mould (Fig. 3(a)) (Ø 65 mm × 60 mm). This pre-determined amount of GFR-HEMS can be thought of as the 100% stacking volume of GFR-HEMS in three phase ESF (Fig. 3(a)). Then the other four stacking volume fractions (80%, 60%, 40%, 20%) were formulated after calculation by weight (or by volume) shown in Fig. 3(b)–(e). Epoxy–hardener, HGMS (S38HS, 3M, USA) and GFR-HEMS (1 layer, 100% stacking volume fraction) with a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio were formulated after calculation. After the preparation steps were implemented, the mixture for the matrix was prepared by mixing the epoxy resin and the hardener continuously together with the hollow glass microspheres for about 10 minutes. The amount of HGMS was fixed at 33.3% by weight (60% volume fraction of the two-phase composite) with respect to the resin mixture in order to increase the viscosity to prevent the macrospheres from floating to the surface during the foam production and further reduce the density of the target ESF. The prepared cured GFR-HEMS were added at regular intervals into the mixture subsequently after the matrix system preparation process was completed within a duration of 10 minutes. Using this procedure, the uncured matrix compound consisting of GFR-HEMS dispersed in the epoxy matrix was achieved. The mixture was poured evenly into the mould and after the mixture was transferred into the mould successfully, a constant load with a standard weight (5.0 kg cm−2) was placed on top of the mould lid to maintain the GFR-HEMS in their well dispersed state. All these preparation procedures are essential in ensuring that the mould will be completely filled and because the amount of GFR-HEMS was obtained in such a way that would restrict the GFR-HEMS from floating to the surface during the foam production. Then the mixture was placed in an oven at 60 °C for 30 minutes and 100 °C for 30 minutes. The composite was taken out of the mould and then left at room temperature to complete the post curing process for 48 hours. The cured composites were cut according to standard dimensions for respective testing after 24 hours.
1 ratio were formulated after calculation. After the preparation steps were implemented, the mixture for the matrix was prepared by mixing the epoxy resin and the hardener continuously together with the hollow glass microspheres for about 10 minutes. The amount of HGMS was fixed at 33.3% by weight (60% volume fraction of the two-phase composite) with respect to the resin mixture in order to increase the viscosity to prevent the macrospheres from floating to the surface during the foam production and further reduce the density of the target ESF. The prepared cured GFR-HEMS were added at regular intervals into the mixture subsequently after the matrix system preparation process was completed within a duration of 10 minutes. Using this procedure, the uncured matrix compound consisting of GFR-HEMS dispersed in the epoxy matrix was achieved. The mixture was poured evenly into the mould and after the mixture was transferred into the mould successfully, a constant load with a standard weight (5.0 kg cm−2) was placed on top of the mould lid to maintain the GFR-HEMS in their well dispersed state. All these preparation procedures are essential in ensuring that the mould will be completely filled and because the amount of GFR-HEMS was obtained in such a way that would restrict the GFR-HEMS from floating to the surface during the foam production. Then the mixture was placed in an oven at 60 °C for 30 minutes and 100 °C for 30 minutes. The composite was taken out of the mould and then left at room temperature to complete the post curing process for 48 hours. The cured composites were cut according to standard dimensions for respective testing after 24 hours.
2.4 Preparation of the three phase epoxy syntactic foam filled with different wall thicknesses of the GFR-HEMS
In order to study the influence of the wall thickness of the GFR-HEMS on the compressive strength of the three phase ESF, GFR-HEMS with different wall thicknesses (1 layer, 2 layers, 3 layers) were added into the two-phase composite to make the three phase ESF. The preparation process was the same as the preparation process shown in Fig. 3. The difference is that the wall thickness is different.2.5 Preparation of the three phase epoxy syntactic foam filled with different volume fractions of the HGMS in the epoxy–hardener system
The volume fraction of the HGMS in the epoxy system also influence the compressive strength of the three phase ESF, HGMS with different volume fractions (40%, 50%, 60%, 70% and 80%) were added into epoxy–hardener system to make the two-phase mixture. Then 80% stacking volume fraction of GFR-HEMS was added into the two-phase mixture to make the three phase ESF. The preparation process was the same as the preparation process shown in Fig. 3.2.6 Characterization
The ESF morphology was captured using a Nikon high definition digital camera. The density of the macrospheres was obtained by the mass divided by volume with 20 macrospheres selected randomly. The glass fiber content used in the GFR-HEMS was tested by Thermogravimetric Analysis (TGA). The density of the ESF was measured in accordance with ASTM D3574. The compression test of the ESF was carried out using a Universal Electromechanical Tester (Instron 4465, Instron Corp., MA) in accordance with ASTM D3575. The SEM morphology of the ESF after compression was measured using a FESEM (JEOL JEM-4701, Japan).3. Results and discussion
3.1 Apparent analysis and density of the GFR-HEMS
Fig. 4 shows a digital image of the GFR-HEMS (2 layers). The diameter of the Petri dish is 10 mm. The surfaces the of GFR-HEMS are all very smooth and the GFR-HEMS are very round, which will be helpful to enhance the mechanical strength of the hollow epoxy macrosphere. The good mechanical strength will be very beneficial to enhance the mechanical strength of the following ESF.Fig. 5 shows the relationship of diameter and density of the GFR-HEMS. The GFR-HEMS diameter and their density distribution can be illustrated in Fig. 5 where 20 reading data (3 types, total 60 data) were taken to ensure a good representation of the overall GFR-HEMS morphology. It can be seen that the diameter distribution of the GFR-HEMS is between 9 mm and 11.2 mm. From Fig. 5, it can be seen that the GFR-HEMS density is mainly distributed in three regions. (a) GFR-HEMS-1 layer, 0.18–0.35 g cm−3 (diameter 9.0–10.2 mm), (b) GFR-HEMS-2 layers 0.41–0.58 g cm−3 (diameter 9.8–11.0 mm), and (c) GFR-HEMS-3 layers 0.51–0.70 g cm−3 (diameter 10.1–11.0 mm), show that the bigger the diameter of the macrosphere, the thicker the wall thickness of the macrosphere, and the higher the density of the macrosphere. The thicker macrospheres are more helpful to improve the compressive strength, but not good for reducing the density of the syntactic foam to a certain extent. So when choosing hollow spheres as a filler, a balance of the strength and the density of the composite is needed in order to achieve the goal of “high strength and low density”. The average density of the GFR-HEMS can be calculated by formula (2).
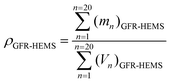 | (2) |
The average density of the GFR-HEMS (ρGFR-HEMS) is the ratio of the mass of all the GFR-HEMS balls 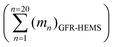 divided by the volume of all the GFR-HEMS balls
divided by the volume of all the GFR-HEMS balls 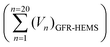 , and the average densities are 0.24 g cm−3 (1 layer), 0.48 g cm−3 (2 layers) and 0.65 g cm−3 (3 layers).
, and the average densities are 0.24 g cm−3 (1 layer), 0.48 g cm−3 (2 layers) and 0.65 g cm−3 (3 layers).
The EPS beads were supplied with a different range of sizes (9–10 mm, 10 kg m−3) and were used as intermediate materials to develop the GFR-HEMS. If the size of the EPS templates are completely consistent, the more layers there are, thus the thicker the sphere wall of the GFR-HEMS is, and the bigger the diameter of the GFR-HEMS, the larger the density of the GFR-HEMS. But the size of the EPS templates are not entirely consistent from 9–10 mm, so Fig. 5 can be used to show the trend of the change in the density with increasing diameter. Also through Fig. 5, the average density can give some guidance to prepare the three phase epoxy syntactic foam, especially in reducing the final foam density.
3.2 Thermogravimetric analysis of the glass fiber content used in the GFR-HEMS
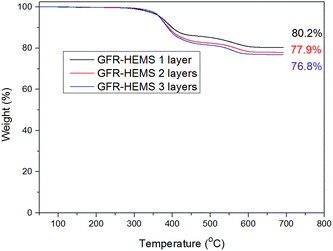
The glass fiber content used in the GFR-HEMS was tested by thermogravimetric analysis (TGA). The TGA data were obtained in an air atmosphere at a heating rate of 50 °C min−1 with a Netzsch TG-209 F3 thermogravimetric analyzer (NETZSCH. Germany). In each case, a GFR-HEMS sample of about 50 mg was examined under a gas flow rate of 20 mL min−1 at temperatures ranging from 50 to 700 °C to evaluate the glass fiber content in the GFR-HEMS. Fig. 6 shows the TG curves of the GFR-HEMS with different layers. The glass fiber volume fraction (ΦGF) can be calculated by formula (3).
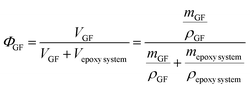 | (3) |
| GFR-HEMS kind | GF content (wt%) | ΦGF (v%) | |
|---|---|---|---|
| 1 | GFR-HEMS 1 layer | 80.2 | 64.1 |
| 2 | GFR-HEMS 2 layers | 77.9 | 60.9 |
| 3 | GFR-HEMS 3 layers | 76.8 | 59.4 |
| Average data | 61.5 ± 2.6 |
In the preparation process of the GFR-HEMS, the glass fiber used is sufficient. So the volume fraction of glass fiber almost does not change in the three kinds of GFR-HEMS with different layers seen from Fig. 6 and Table 1. The volume fraction of glass fiber in the GFR-HEMS is about 61.5% ± 2.6%. The density of the GFR-HEMS sphere wall can be calculated by formula (4).
| ρsphere wall = ΦGFρGF + (1 − ΦGF)ρepoxy system | (4) |
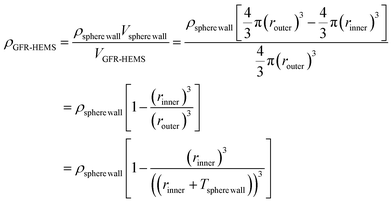 | (5) |
| GFR-HEMS kind | rinner (cm) | ρsphere wall (g cm−3) | ρGFR-HEMS (g cm−3) | Tsphere wall (cm) | |
|---|---|---|---|---|---|
| 1 | GFR-HEMS 1 layer | 0.475 | 1.99 | 0.24 | 0.0208 (208 μm) |
| 2 | GFR-HEMS 2 layers | 0.475 | 1.99 | 0.48 | 0.0458 (458 μm) |
| 3 | GFR-HEMS 3 layers | 0.475 | 1.99 | 0.65 | 0.0669 (669 μm) |
The data shows the prediction thicknesses of the sphere walls of the GFR-HEMS. But these data are not the real data, they need to be carefully validated with real data. SEM images can give us the intuitive visual data.
3.3 Microstructure analysis of the GFR-HEMS and epoxy syntactic foam
SEM experiments were performed to find the trend of the change in the sphere wall thickness of the GFR-HEMS in the foam. In the sample preparation process, the samples were randomly selected and taken out for SEM tests. Fig. 7 shows the SEM images of the three phase ESF with different layer GFR-HEMS. It can been seen that the wall thickness of the different layer GFR-HEMS is different, but the total trend seen from Fig. 7(a1)–(c1) is that the thickness is increasing with the increasing layers. In addition, the thickness of the same layer GFR-HEMS is also different, as seen from Fig. 7(a1)–(a3). So we use the layer number to classify the GFR-HEMS. And the density of the GFR-HEMS is also measured by the average density. The thicknesses of the sphere walls of the GFR-HEMS in the ESF are summarized in Table 3.| Tsphere wall (μm) | GFR-HEMS kind | 1# | 2# | 3# | The average thickness from SEM | Caculated by formula (5) |
|---|---|---|---|---|---|---|
| 1 | 1 layer | 192 | 233 | 233 | 219 ± 27 | 208 |
| 2 | 2 layers | 417 | 457 | 533 | 469 ± 64 | 458 |
| 3 | 3 layers | 647 | 667 | 733 | 682 ± 51 | 669 |
From Table 3, it can be seen that the average thickness calculated by formula (5) almost is the same as the average thickness from SEM. This means that the calculations are correct. The calculation is based on the data from Fig. 5, so Fig. 5 can not only be used to show the trend of the change in the density with increasing diameter, but also can give us some guidance to prepare the three phase epoxy syntactic foam, especially in reducing the final foam density.
Some of the layers (as shown in the SEM images in Fig. 7) seem very homogeneous and indeed are playing an important role in enhancing the compressive strength of the foam. The cellular structure developed in the matrix can give a more lightweight structure in the foam, so the structure is also important in reducing the density of the foam. Therefore it needs to be taken into account as a void/cellular structure and its characterization is important as it has a major impact on the final compressive strength and density of the foam.
In addition, it also can be seen that there is almost no interface between the two phases (sphere wall and epoxy–HGMS system) in all the SEM images in Fig. 7. The combination of the sphere wall phase and epoxy–HGMS system phase is close. In the section of the mechanical enhancement mechanism of the GFR-HEMS in the ESF, Fig. 7(b2) will be carefully discussed as a representative in Section 11.
3.4 Macrostructure analysis of the epoxy syntactic foam
Fig. 8 shows a digital image of the ESF showing the matrix porosity, GFR-HEMS and PS particles. The image shows the typical microstructure of the epoxy syntactic foam prepared in this study. The hollow spheres are dispersed randomly in the foam. The foam is cut into two parts, not all the GFR-HEMS are cut from the middle, so the cellular structure exhibits a very heterogeneous morphology. The inner walls of the hollow epoxy macrospheres are all very neat and smooth because of the role of the EPS bead templates. The regular spherical wall can increase the compressive strength of the macrospheres. Two types of porosity appeared in the foam, which were contributed to by the hollow epoxy macrospheres and matrix (epoxy + HGMS). The hollow epoxy macrosphere porosity can be controlled by selecting the type and size of the hollow epoxy macrosphere. However, the matrix porosity could be attributed to air entrapment, which resulted in the formation of voids within the matrix during the mixing and coating procedure.Although an increase in porosity would undermine the mechanical properties of the foam system, this can also be considered an advantage to adjust the overall density and properties of the system. The epoxy syntactic foam contains GFR-HEMS and HGMS in the epoxy matrix. The HGMS added in the epoxy matrix can increase the viscosity of the matrix to hinder the floating of the GFR-HEMS. So GFR-HEMS can be uniformly dispersed in the matrix resin in the curing process. The ESF can be used as a buoyancy material to offset the gravity of oil pipes and other equipment used in deepwater oil exploration.
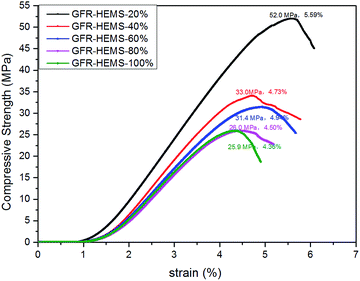
3.5 Influence of the stacking volume fraction of the GFR-HEMS on the compressive properties of the three phase epoxy syntactic foam
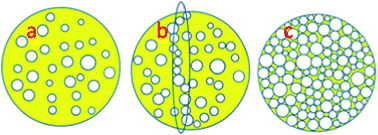
Fig. 9 shows the influence of the stacking volume fraction of the GFR-HEMS on the compressive properties of the three phase ESF. When the volume fraction of the HGMS in the epoxy system is 60%, the compressive strength of the three phase ESF decreases with the increasing GFR-HEMS content from 61.4 MPa (0% GFR-HEMS) to 52.0 MPa (20% GFR-HEMS), 33.0 MPa (40% GFR-HEMS), 31.4 MPa (60% GFR-HEMS), 26.0 MPa (80% GFR-HEMS) and 25.9 MPa (100% GFR-HEMS). Several conclusions can be obtained from analysis of the above data.The compressive strength values of the three phase ESF (Fig. 9) are 52.0 MPa (20%), and 33.0 MPa (40%), about 84.7% (52.0/61.4) and 53.7% (33.0/61.4) of the ESF without the GFR-HEMS (0%, epoxy–HGMS composite), respectively, indicating that the 40% addition of the GFR-HEMS already makes the compressive strength of the three phase ESF reach the percolation point. The rapid reduction of the compressive strength of the three phase ESF is induced by the increasing defects in the composite because of the addition of the GFR-HEMS. The defects are shown in Fig. 8. As seen from Fig. 8, the defects include the GFR-HEMS themselves, the matrix porosity, the HGMS and the contact interface between the GFR-HEMS and the epoxy–hardener–HGMS system. The contact interface between the GFR-HEMS and the epoxy–hardener–HGMS system increases with increasing GFR-HEMS content, and the matrix porosity may also increase with the increasing GFR-HEMS content in the mixing progress because of the air intervention. In addition, the percolation theory can be used to explain the trend of the mechanical strength change. Fig. 10 shows the dispersion model of the GFR-HEMS spherical filler in the epoxy–hardener–HGMS system. Before the percolation point of the GFR-HEMS in the foam (Fig. 10(a)), there is almost no contact between the hollow spheres. There is almost no contact defect. The compressive strength is kept at a high level (52.0 MPa), and only a little lower than that of the foam with the GFR-HEMS (61.4 MPa). Fig. 10(b) shows the 40% GFR-HEMS dispersion state in the epoxy–hardener–HGMS system. The contact rate of the GFR-HEMS in contact with each other increases rapidly after exceeding the percolation point (Fig. 10(b)), the compressive strength will decrease rapidly because of the GFR-HEMS contact. The above defects make the compressive strength of the three phase ESF decrease with the increasing GFR-HEMS. After the percolation point of the GFR-HEMS in the foam (take 100% (Fig. 10(c)) for example), there are many contact defects between the GFR-HEMS. The compressive strength will decrease gradually with the increasing GFR-HEMS contact defects.
 | ||
| Fig. 10 Dispersion model of the GFR-HEMS spherical filler in the epoxy–hardener–HGMS system (a-20%, b-40%, c-100%). | ||
As seen from Fig. 9, it also can be concluded that the deformation rate and compressive strength changes of the three phase ESF have the same trend. The deformation rate almost decreases with the increasing GFR-HEMS content. The deformation rate decreased from 5.59% (20%) to 4.73% (40%), 4.94% (60%), 4.50% (80%) and 4.36% (100%), which can also be explained by the defects induced by GFR-HEMS addition, especially by the defects of the matrix porosity and the contact interface.
The compressive strength values of the three phase ESF are 31.4 MPa (60%), 26.0 MPa (80%) and 25.9 MPa (100%), about 51.1% (31.4/61.4), 42.3% (26.0/61.4) and 42.2% (25.9/61.4) of the ESF without the GFR-HEMS (0%, epoxy–HGMS composite), respectively. The reducing trend of compressive strength becomes flat gradually, and the compressive strength data basically maintain the steady decline curve. Compressive strength (80%) and compressive strength (100%) are almost the same, showing that compressive strength is almost not influenced by GFR-HEMS content. So in order to maintain sufficient compressive strength and at the same time, get large enough buoyancy at low density, we can add GFR-HEMS because the more GFR-HEMS content added in the three phase ESF, the better the buoyancy properties which includes high compressive strength and low density. 100% GFR-HEMS content added in the three phase ESF is the best state to get enough buoyancy at this time.
3.6 Influence of the wall thickness of the GFR-HEMS on the compressive properties of the three phase epoxy syntactic foam
Not only stacking the volume fraction of the GFR-HEMS, the wall thickness of the GFR-HEMS also influences the compressive strength of the three phase ESF. Fig. 11 shows the influence of the wall thickness of the GFR-HEMS on the compressive strength of the three phase ESF. From the above Section (3.3), the compressive strength of the three phase ESF with 2 layers decreases with increasing GFR-HEMS content, and the compressive strength change of the three phase ESFs with 1 layer and 3 layers also have the same trend. In addition, one clear phenomenon can be found that the compressive strength of the three phase ESF with 3 layers is the highest of all three samples with the same stacking volume fraction of GFR-HEMS in the three phase ESF, the compressive strength of the three phase ESF with 2 layers is second, and the compressive strength of the three phase ESF with 1 layer is the lowest. The above phenomenon indicates that the compressive strength of the three phase ESF increases with the increasing wall thickness of the GFR-HEMS (layers) filling the ESF.With the stacking volume fraction of the GFR-HEMS at 20% as an example, the compressive strength of the three phase ESF increases from 41.3 MPa (1 layer), 52.0 MPa (2 layers) and 57.8 MPa (3 layers), about 67.3% (41.3/61.4, 1 layer), 84.7% (52.0/61.4, 2 layers) and 94.1% (57.8/61.4, 3 layers) of the ESF without GFR-HEMS, respectively, showing that GFR-HEMS with higher wall thickness not only can be used to improve the sphere strength itself but also improve the strength of the three phase ESF.
When the stacking volume fraction of the GFR-HEMS is 100%, the compressive strength of the three phase ESF increases from 16.9 MPa (1 layer), 25.9 MPa (2 layers) and 31.0 MPa (3 layers), showing that the wall thickness of the GFR-HEMS influences the compressive strength clearly. So in order to maintain sufficient compressive strength, the wall of the GFR-HEMS can be thickened which means the compressive strength will be better. But at the same time, the density of the three phase ESF which is related to the buoyancy property should also be addressed.
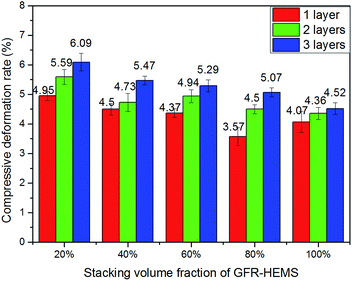
Fig. 12 shows the influence of the wall thickness of the GFR-HEMS on the compressive deformation rate of the three phase ESF. As seen from Fig. 12, it can be concluded that the deformation rate and compressive strength changes of the three phase ESF have the same trend not only at low stacking volume fraction but also at high stacking volume fraction of the GFR-HEMS in the composite, all increase with the increasing GFR-HEMS wall thickness. When the stacking volume fraction of the GFR-HEMS in the composite is at 20%, the deformation rate increases from 4.95% (1 layer) to 5.59% (2 layers) and 6.09% (3 layers). Although the data deformation changing rate is small, it also indicates that the increasing GFR-HEMS wall thickness not only increases the anti-deformation ability of the GFR-HEMS themselves, but also increases the anti-deformation ability of the three phase epoxy syntactic foam.
3.7 Influences of the stacking volume fraction of the GFR-HEMS and the wall thickness of the GFR-HEMS on the density of the three phase epoxy syntactic foam
The main purpose of using centimeter-sized lightweight epoxy hollow sphere GFR-HEMS in the ESF is in order to ensure the strength of the three phase material and at the same time, as far as possible to reduce the density of the three phase ESF, so as to improve the buoyancy compensation ability of the three phase ESF. Fig. 13 shows the influence of the stacking volume fraction of the GFR-HEMS and the wall thickness of the GFR-HEMS on the density of the three phase ESF. As seen from Fig. 13(a), the density of the three phase ESF decreases with the increasing GFR-HEMS (1 layer) volume fraction from 0.676 g cm−3 (0%) to 0.62 g cm−3 (20%), 0.58 g cm−3 (40%), 0.55 g cm−3 (60%), 0.48 g cm−3 (80%) and 0.46 g cm−3 (100%). When the density of the three phase ESF is 0.58 g cm−3 (40%) and 0.48 g cm−3 (80%), the compressive strength is 26.4 MPa (40%) and 17.6 MPa (80%), respectively, showing that the density decreases with increasing GFR-HEMS content, and compressive strength also decreases with increasing GFR-HEMS content.When the lightweight composite is used as a buoyancy material, the lower the density the better the buoyancy properties when the compressive strength is kept constant. On the other hand, the higher the compressive strength the better the buoyancy properties when the density is kept constant. Higher compressive strength and lower density are often contradictory in buoyancy materials, so a balance should be found between them in order to achieve the best combination of “high strength and low density”.
The density change trend with the increasing stacking volume fraction of the GFR-HEMS with 2 layers (Fig. 13(b)) is the same as the density change trend with 1 layer. The density with 2 layers decreases with the increasing GFR-HEMS content from 0.676 g cm−3 (0%) to 0.67 g cm−3 (20%), 0.64 g cm−3 (40%), 0.63 g cm−3 (60%), 0.60 g cm−3 (80%) and 0.58 g cm−3 (100%), which are all higher than the density with 1 layer with the same content, showing that a greater thickness of the GFR-HEMS makes the three phase ESF have a higher density. But only when the GFR-HEMS stacking volume fraction with 2 layers is higher than 80%, the density will be reduced to below 0.6 g cm−3, the corresponding compressive strength values are 26.0 MPa (80%) and 25.9 MPa (100%), which are higher than the compressive strength of the three phase ESF filled with 1 layer GFR-HEMS.
Adding two layers of hollow spheres can improve the compressive strength of the composite, but can also increase the density of the composite, which reduces the buoyancy compensation ability of the composite material. In this case, the maximum content of GFR-HEMS should be added into the composite to reduce the density of the three phase ESF. 100% stacking volume fraction of GFR-HEMS is the best choice.
Because the density of the GFR-HEMS with 3 layers is 0.65 g cm−3, the same as that of the two-phase epoxy–HGMS composite (0.676 g cm−3), the density of the three phase ESF distributes between 0.67 g cm−3 and 0.68 g cm−3, and almost does not change after adding the GFR-HEMS as seen in Fig. 13(c), showing that the addition of GFR-HEMS has no effect on reducing the density of the composite. At the same time, the addition of GFR-HEMS increases the defects of the three phase ESF, which decreases its compressive strength. In addition, the addition of GFR-HEMS also makes the ESF preparation process become complicated and increases the preparation cost. The compressive strength values of the three phase ESF with 3 layers of GFR-HEMS are all higher than those of the three phase ESFs with 2 layers and 1 layer of GFR-HEMS from the above compressive strength data. However the addition of GFR-HEMS with 3 layers has no effect on reducing the density of the three phase ESF, so reducing the density of the three phase ESF is limited through increasing the GFR-HMES layers and obtaining higher compressive strength at the same time.
It can be concluded that increasing the stacking volume fraction of the GFR-HEMS with 1 layer and 2 layers can reduce the density of the three phase ESF. In addition, increasing the wall thickness of the GFR-HEMS can increase the compressive strength of the three phase ESF, but can increase the density of ESF at the same time. Increasing the compressive strength is limited through increasing the wall thickness of the GFR-HEMS and maintaining low density at the same time. The wall thickness of the GFR-HEMS should be less than 3 layers. 100% stacking volume fraction of the GFR-HEMS with 2 layers may be a good choice to make the three phase ESF show good comprehensive performance. The corresponding compressive strength and density are 25.9 MPa and 0.58 g cm−3, respectively. The compressive strength and density of the three phase ESF studied by Samsudin37 are 19.7 MPa and 0.566 g cm−3, respectively. From the data above, one can conclude that the three phase ESF shows better comprehensive performance in this study. 25.9 MPa and 0.58 g cm−3 are the best combination of “high strength and low density” in this study.
3.8 Influence of the HGMS content in the epoxy–hardener system on the compressive strength of the three phase epoxy syntactic foam
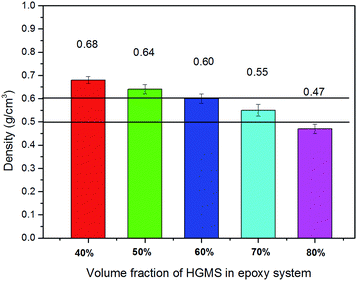
Fig. 14 shows the influence of the volume fraction of the HGMS in the epoxy–hardener system on the compressive properties of the three phase ESF. When the stacking volume fraction of the GFR-HEMS in the mould is 80%, the compressive strength of the three phase ESF increases with the increasing HGMS volume fraction in the epoxy–hardener system from 20.5 MPa (40%) to 23.9 MPa (50%), 26.0 MPa (60%), 27.4 MPa (70%), and then decreases to 15.1 MPa (80%). This phenomenon can be illustrated by the structure characteristics of the digital images in Fig. 15. Fig. 15 shows digital images of the three phase epoxy syntactic foams.Especially when the HGMS content in the epoxy–hardener system is low, a floating phenomenon of the GFR-HEMS is very easy to occur in the curing process of the thermosetting epoxy resin because of the lower density of the GFR-HEMS and the low viscosity of the epoxy system at high temperature, leading to the delamination phenomenon of the three phase ESF. The lower the HGMS content in the epoxy–hardener system, the more obvious the floating phenomenon, and the more obvious the delamination phenomenon of the three phase ESF is. As seen from Fig. 15, there are no GFR-HEMS at the bottom of the 40% and 50% samples and the delamination phenomenon of the three phase ESF is very obvious in the five samples. There almost is no delamination phenomenon in the 60% sample three phase ESF and the GFR-HEMS disperse uniformly in the matrix. A higher viscosity of the epoxy–HGMS system (60%) can prevent the floating phenomenon.
With the increasing HGMS volume fraction in the epoxy system, the compressive strength of the three phase ESF increases to 27.4 MPa (70%), which is the highest compressive strength. But the HGMS filled in epoxy system is limited, Φmax is about 60–70% according to the “parametric theory of the random packing of particles” from the previous analysis in the introduction.27–29 After Φmax, the HGMS are in contact with each other and the HGMS would rupture under the pressure in the preparation process, then the compressive strength of the three phase ESF decreases to 15.1 MPa (80%). So in the three phase ESF, higher HGMS content in the epoxy–hardener system is not better. Proper HGMS content should be considered in the preparation process of the three phase ESF. Here 60 v% of HGMS in the epoxy–hardener system may be the proper choice.
3.9 Influence of the HGMS content in the epoxy–hardener system on the density of the three phase epoxy syntactic foam
Fig. 16 shows the influence of the volume fraction of the HGMS in the epoxy–hardener system on the density of the three phase ESF. From Fig. 16, it can be seen that the density of the three phase ESF decreases with increasing HGMS content from 0.68 g cm−3 (40%) to 0.64 g cm−3 (50%), 0.60 g cm−3 (60%), 0.55 g cm−3 (70%) and 0.47 g cm−3 (80%), showing that adding HGMS is useful to reduce the density of the three phase ESF and provide greater buoyancy. The effect of adding the HGMS and GFR-HEMS are equally important to reduce the density of the three phase ESF. Although great addition of the HGMS greatly reduces the density of the three phase ESF, the other properties such as compressive strength should also be considered. Deciding the optimum added content of the HGMS needs comprehensive consideration of the ESF properties. Here 60% is lower than the maximum volume fraction of HGMS in the epoxy system, and the viscosity of the mixture is also suitable to add GFR-HEMS in the mixture, this is why the 60% volume fraction addition of the HGMS is chosen to add a different content of the GFR-HEMS above.3.10 Mechanical rupture behaviour of the epoxy syntactic foam
In order to know the rupture process of the three phase ESF in the universal testing machine during the compression process, the cured big epoxy syntactic foam (300 mm × 300 mm) was cut into small squares (60 mm × 60 mm × 60 mm) to perform the compression test. The compressive strength–stain curve of the ESF is shown in Fig. 17. The compressive strength of the syntactic foam is about 27.3 MPa, about 2730 meters water pressure, which is almost the same as the compressive strength of the syntactic foam using a cylinder sample as a test specimen above (25.9 MPa). The compressive strength data is in the range of the measurement error. | ||
| Fig. 17 Compressive strength–stain curve of the ESF (volume fraction of the HGMS in the epoxy system is 60%, the stacking volume fraction of the GFR-HEMS (2 layers) in the mould is 100%). | ||
The compressive behaviour displayed by the syntactic foam is comparable to other syntactic foam systems, which utilize other thermoset matrices and glass microspheres as their constituents.2 The compressive strength drop at 4.4% can be related to the occurrence of crack initiation in the matrix as can be seen from the progressive cell collapse image included in Fig. 17.35 At this stage, compression of the material resulted in a filling up of the matrix porosity due to the rupture of the porous feature. Further compression caused the formation of a shear crack in the longitudinal direction (i.e. the direction of compression).2 The longitudinal crack grew quickly in several seconds after the crack beginning. At this stage, further compression of the material resulted in more filling up of the matrix porosity due to the rupture of the porous feature. The fracture mechanism in this region involved the crushing of the GFR-HEMS, and similar observations were also reported by Kim, Ming Yu and so on.38,39 Besides sphere crushing, the failure of the GFR-HEMS can also be attributed to debonding (i.e. interfacial fracture between the matrix and GFR-HEMS) at the surfaces of the GFR-HEMS. However, the presence of voids in the GFR-HEMS limits the occurrence of debonding and promotes a higher failure mechanism through the rupture of the sphere wall because such fracture is faster than debonding. In addition, as seen from Fig. 17, most of the GFR-HEMS were intact, showing the prevention effect of the GFR-HEMS on the cracking of the foam.
The average density of the syntactic foam system is about 570 kg m−3, providing about 430 kg m−3 buoyancy when the ESF is used in deepwater oil exploration. The syntactic foam with the same structure has been used in deepwater oil explorations shown in a United States patent (no. US 7121767 B1, rugged foam buoyancy modules and method of manufacture) and the Buoyancy product of Balmoral Offshore company and other companies. The lower density is due to the utilization of the GFR-HEMS and HGMS, which can effectively reduce the density of the foam and also provide a way of reducing the production cost which is attributed to the low price of the EPS bead templates and glass fiber compared to the other types of hollow spheres available in the market.
3.11 Mechanical enhancement mechanism of the GFR-HEMS in the ESF
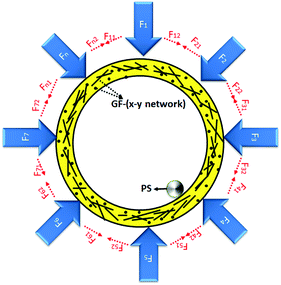
Fig. 18 shows the SEM image of the three phase ESF. As seen from Fig. 18, the matrix resins of the sphere wall and epoxy–HGMS system are all the same kind of epoxy system (Huntsman 1564/3486 epoxy resin system). There is almost no interface between the two phases (sphere wall (b) and epoxy–HGMS system (c)). The combination of the b phase and c phase is close. Interfacial fracture between the epoxy–HGMS system and the GFR-HEMS does not happen so easily. This can be illustrated by the longitudinal crack in Fig. 17. The hollow spheres are destroyed by the longitudinal crack, and there is almost no debonding phenomenon occurrence in Fig. 17, similar observations were also reported by Samsudin.37 The presence of voids in the GFR-HEMS limits the occurrence of debonding and promots a higher failure mechanism through the rupture of the sphere wall because such fracture is faster than debonding.38,39The sphere inner surface (Fig. 18(a)) of GFR-HEMS keeps a good radian because of the effect of the EPS bead, which will make GFR-HEMS transfer force along the sphere surface when GFR-HEMS is pressed by external force. In the sphere wall (Fig. 18(b)), the glass fiber dispersed uniformly in the epoxy matrix and the glass fiber and epoxy resin are closely bonded together, showing that the “rolling ball method” is a very appropriate method to make a glass fiber reinforced epoxy resin in the macrosphere preparation process. The thickness of the macrosphere wall is about 457 μm and the thickness distribution is also very uniform. This is because the centrifugal force and the pressure of the rolling ball machine can make glass fiber uniformly disperse in the epoxy resin and ensure that the sphere wall thickness is uniform.
The forces (the centrifugal force & the pressure) can also make glass fibers form a fiber spherical x–y network throughout the macrosphere epoxy matrix. Almost all of the fiber direction in the network are vertical to the sphere center direction (diameter direction, z-direction) in Fig. 18(b). When GFR-HEMS are used in the three phase ESF, the structure of the fiber spherical x–y network can make the GFR-HEMS and the three phase ESF have great compressive strength.
Fig. 19 shows the mechanical enhancement mechanism of the GFR-HEMS. When the GFR-HEMS are pressed by the forces from different directions in the composite, the forces can be decomposed into forces in different directions by the spherical structure. When the GFR-HEMS are under isostatic pressure, the forces can be considered equal, so F1 = F2 = F3 = F4 = F5 = F6 = F7 = …… = Fn and then F11 = F12 = F21 = F22 = F31 = F32 = F41 = F42 = F51 = F52 = F61 = F62 = F71 = F72 = …… = Fn1 = Fn2 in Fig. 19. The divided forces can transfer through the glass fiber spherical x–y network of the GFR-HEMS, so most of the forces can be offset. Only a very small force transfers along the axial direction (z-direction), so it needs tremendous pressure to destroy the GFR-HEMS. These are reasons why the three phase ESF has such a high compressive strength.
4. Conclusions
The prepared GFR-HEMS using the “rolling ball method” showed great potential in replacing HGMS, due to their simple production method and low cost production strategy because they do not utilize any expensive specialized equipment during their processing procedure which can be implemented at ambient temperature. The preparation of the ESF/GFR-HEMS/HGMS syntactic foams and their compressive properties were investigated in the present study. The main conclusions can be summarized as follows.(a) The “rolling ball method” can make glass fibers form a fiber spherical x–y network throughout the macrosphere to make the GFR-HEMS and the three phase ESF have great compressive strength. The produced ESF has relatively high compressive strength and low density, and thus has the potential to be used in deepwater oil exploration.
(b) The compressive strength of the three phase ESF (HGMS, 60%) decreases with increasing GFR-HEMS stacking volume fraction, which is induced by the increasing defects in the composite. The defects include the GFR-HEMS themselves, the matrix porosity, the HGMS and the contact interface between the GFR-HEMS and the epoxy–hardener–HGMS system. In order to maintain a sufficient compressive strength and, at the same time, get a large enough buoyancy at low density, more GFR-HEMS content can be added in the three phase ESF to obtain the better the buoyancy properties. 100% GFR-HEMS content added in the three phase ESF is the best state to get enough buoyancy at this time.
(c) When the stacking volume fraction of the GFR-HEMS is 100%, the compressive strength of the three phase ESF increases from 16.9 MPa (1 layer), 25.9 MPa (2 layers) and 31.0 MPa (3 layers), showing that the wall thickness of the GFR-HEMS influences the compressive strength clearly. The thicker the wall of the GFR-HEMS, the better the compressive strength. Increasing the compressive strength is limited through increasing the wall thickness of the GFR-HEMS and maintaining a low density at the same time. The wall thickness of the GFR-HEMS should be less than 3 layers. 100% stacking volume fraction of the GFR-HEMS with 2 layers may be a good choice to make the three phase ESF show good comprehensive performances.
(d) With the increasing HGMS volume fraction in the epoxy–hardener system, the compressive strength of the three phase ESF increases to 27.4 MPa (70%), and then decreases to 15.1 MPa (80%). So in the three phase ESF, the higher HGMS content in the epoxy–hardener system is not better. The mixture material viscosity should be considered in the preparation process. Proper HGMS content should be considered in the preparation process of the three phase ESF.
(e) Some of the layers seem very homogeneous and indeed are playing an important role in enhancing the compressive strength of the foam. The cellular structure developed in the matrix can give more lightweight structure in the foam, so the structure is also important in reducing the density of the foam. Therefore it needs to be taken into account as a void/cellular structure and its characterization is important as it has a major impact in the final compressive strength and the density of the foam.
Acknowledgements
The work was supported by the Special Fund of the National Priority Basic Research of China (2014CB239503), the National Natural Science Foundation of China (51403124, 51303034), Project Funded by the China Postdoctoral Science Foundation (2015M571459) and State Key Laboratory for Modification of Chemical Fibers and Polymer Materials, Donghua University (LK1419).Notes and references
- G. Tagliavia, M. Porfiri and N. Gupta, J. Compos. Mater., 2009, 43, 561–582 CrossRef CAS PubMed
.
- N. Gupta, R. Ye and M. Porfiri, Composites, Part B, 2010, 41, 236–245 CrossRef PubMed
.
- L. Zhang and J. Ma, Compos. Sci. Technol., 2010, 70, 1265–1271 CrossRef CAS PubMed
.
- N. Gupta and E. Woldesenbet, Compos. Struct., 2003, 61, 311–320 CrossRef
.
- M. M. Islam and H. S. Kim, J. Sandwich Struct. Mater., 2012, 14, 111–127 CrossRef CAS PubMed
.
- M. Narkis, S. Kenig and M. Puterman, Polym. Compos., 1984, 5, 159–165 CrossRef PubMed
.
- M. Yu, P. Zhu and Y. Ma, Mater. Des., 2013, 47, 80–89 CrossRef CAS PubMed
.
- M. Yu, P. Zhu and Y. Ma, Comput. Mater. Sci., 2012, 61, 89–98 CrossRef PubMed
.
- L. Peroni, M. Scapin, M. Avalle, J. Weise and D. Lehmhus, Mater. Sci. Eng., A, 2012, 552, 364–375 CrossRef CAS PubMed
.
- S. Ji, D. Srivastava, N. J. Parker and I. Lee, Polymer, 2012, 53, 205–212 CrossRef CAS PubMed
.
- P. Yu and M. Qian, Mater. Chem. Phys., 2012, 137, 435–438 CrossRef CAS PubMed
.
- J.-Z. Liang, Composites, Part B, 2014, 56, 431–434 CrossRef CAS PubMed
.
- F. N. Gu, W. G. Lin, J. Y. Yang, F. Wei, Y. Wang and J. H. Zhu, Microporous Mesoporous Mater., 2012, 151, 142–148 CrossRef CAS PubMed
.
- T. A. Vereshchagina, S. N. Vereshchagin, N. N. Shishkina, O. A. Mikhaylova, L. A. Solovyov and A. G. Anshits, Microporous Mesoporous Mater., 2013, 169, 207–211 CrossRef CAS PubMed
.
- C. Yuan, B. Zeng, S. Yu, J. Mao, X. Chen, W. Luo, Y. Xu, F.-C. Chang and L. Dai, RSC Adv., 2014, 4, 4796–4803 RSC
.
- C. Yuan, J. Li, L. Hou, J. Lin, G. Pang, L. Zhang, L. Lian and X. Zhang, RSC Adv., 2013, 3, 18573–18578 RSC
.
- J. Yu, Z. Li, Q. Liu, J. Wang, H. Wei, M. Zhang and L. Liu, RSC Adv., 2013, 3, 6621–6626 RSC
.
- J. Yu, Y. Le and B. Cheng, RSC Adv., 2012, 2, 6784–6791 RSC
.
- A.-X. Wang, D.-Q. Chu, L.-M. Wang, B.-G. Mao, H.-M. Sun and Z.-C. Ma, RSC Adv., 2014, 4, 7545–7548 RSC
.
- Z.-Q. Shi, L.-X. Jiao, J. Sun, Z.-B. Chen, Y.-Z. Chen, X.-H. Zhu, J.-H. Zhou, X.-C. Zhou, X.-Z. Li and R. Li, RSC Adv., 2014, 4, 47–53 RSC
.
- R. Panigrahi and S. K. Srivastava, RSC Adv., 2013, 3, 7808–7815 RSC
.
- W. Cai, W. Wang, Y. Yang, G. Ren and T. Chen, RSC Adv., 2014, 4, 2295–2299 RSC
.
- S. Beesabathuni, J. Stockham, J. Kim, H. Lee, J. Chung and A. Shen, RSC Adv., 2013, 3, 24423–24429 RSC
.
- Q. Xie, H. Guo, X. Zhang, A. Lu, D. Zeng, Y. Chen and D.-L. Peng, RSC Adv., 2013, 3, 24430–24439 RSC
.
- R. Liu, W. Du, Q. Chen, F. Gao, C. Wei, J. Sun and Q. Lu, RSC Adv., 2013, 3, 2893–2896 RSC
.
- T. C. Lin, N. Gupta and A. Talalayev, J. Mater. Sci., 2009, 44, 1520–1527 CrossRef CAS
.
- X. Z. An, S. S. He, H. D. Feng and Q. Qian, Appl. Phys. A: Mater. Sci. Process., 2015, 118, 151–162 CrossRef CAS
.
- P. S. Yerazunis, S. W. Cornellamp and B. Wintner, Nature, 1965, 835–837 CrossRef PubMed
.
- A. B. Yu and N. Standish, Powder Technol., 1988, 55, 171–186 CrossRef CAS
.
- N. Gupta, Kishore, E. Woldesenbet and S. Sankaran, J. Mater. Sci., 2001, 36, 4485–4491 CrossRef CAS
.
- N. Gupta, E. Woldesenbet and Kishore, J. Mater. Sci., 2002, 37, 3199–3209 CrossRef CAS
.
- H. S. Kim and M. A. Khamis, Composites, Part A, 2001, 32, 1311–1317 CrossRef
.
- H. S. Kim and H. H. Oh, J. Appl. Polym. Sci., 2000, 76, 1324–1328 CrossRef CAS
.
- K. Yung, B. Zhu, T. Yue and C. Xie, Compos. Sci. Technol., 2009, 69, 260–264 CrossRef CAS PubMed
.
- R. Caeti, N. Gupta and M. Porfiri, Mater. Lett., 2009, 63, 1964–1967 CrossRef CAS PubMed
.
- C. Karthikeyan and S. Sankaran, Mater. Lett., 2004, 58, 995–999 CrossRef CAS PubMed
.
- S. S. Samsudin, Z. M. Ariff, Z. Zakaria and A. A. Bakar, eXPRESS Polym. Lett., 2011, 5, 653–660 CrossRef CAS
.
- H. S. Kim and P. Plubrai, Composites, Part A, 2004, 35, 1009–1015 CrossRef PubMed
.
- M. Yu, P. Zhu and Y. Ma, Comput. Mater. Sci., 2012, 63, 232–243 CrossRef PubMed
.
| This journal is © The Royal Society of Chemistry 2015 |