High-performance microwave absorption of flexible nanocomposites based on flower-like Co superstructures and polyvinylidene fluoride†
Abstract
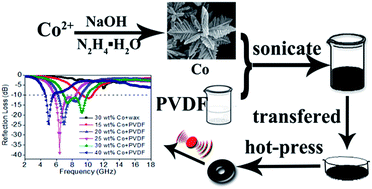
Flower-like Co superstructures were synthesized via a facile hydrothermal process at low temperature; then the flexible Co/PVDF nanocomposites were prepared by combining the Co nanocrystal with a polyvinylidene fluoride (PVDF) matrix. The Co/PVDF hybrids exhibit distinct microwave absorption properties in the range of 2–18 GHz. With filler loading of 25 wt%, the minimum reflection loss reaches −38.9 dB at 6.4 GHz as the thickness is 2.5 mm. The frequency bandwidth less than −10 dB covers from 4.64 to 10.56 GHz by adjusting the weight content from 15 wt% to 40 wt%. The possible microwave absorbing mechanism has been also discussed in detail.

 Please wait while we load your content...
Please wait while we load your content...