Effect of compressive strain on the Hertzian contact of self-mated fluorinated carbon films

Abstract

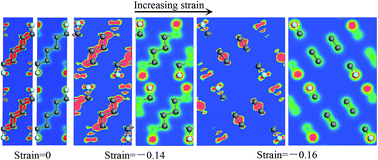
Recent research on carbon films has introduced interesting low friction properties of self-mated fluorinated carbon films. In particular, the low friction mechanism of self-mated fluorinated carbon films was consistently attributed to anti-bonding repulsive forces. However, no experimental data reported to date for the limitations of this low friction mechanism comply with the results obtained using first-principles calculations. In this investigation, we attempt to clarify the limitations of the low friction mechanism of self-mated fluorinated carbon films.

---

1. Introduction

Active research on diamond-like carbon (DLC) films has revealed not only excellent tribological properties,^1–3 but also has prepared the ground for the discovery of several diamond-like carbon based materials. The preparation of foreign atom doped DLC films can improve their tribological behavior.^4,5 In particular, fluorinated DLC films, which exhibit ultralow friction under high vacuum, have been reported.⁶

Due to the difficulties in the direct observation of the friction processes using in situ experiments with atomic resolution, it is not trivial to understand the contribution of each mechanism. However, first-principles and molecular dynamic (MD) simulations are treated as powerful tools to capture atomic details and gain a deeper insight into the low friction mechanism of self-mated fluorinated carbon films at the nanoscale. Most research, which is based on first-principles and MD simulations, reported that the low friction mechanism of self-mated fluorinated carbon films is attributed to anti-bonding repulsive forces.^7–9 However, does such anti-bonding repulsive forces maintain the low friction of self-mated fluorinated carbon films with increase in contact pressure? Therefore, it is necessary to obtain the contact pressure limit of self-mated fluorinated diamond system through the uniaxial compression of the self-mated fluorinated diamond system using first-principles methods. Of course, a detailed tribological investigation should take into account numerous variables such as temperature, sliding velocity or magnitude of the lateral forces.¹⁰ A detailed comprehensive investigation of the dynamic compressive properties of the self-mated diamond system sliding is beyond the scope of this study. In addition, the amorphous carbon film surface was often represented by a diamond surface following the common practice used in the literature by employing diamond as a model to study the amorphous carbon surfaces.^11–14 Moreover, in the our previous study, we successfully predicted the failure mechanism of fluorinated amorphous carbon films using fluorinated diamond surfaces.¹⁵ Here, in this article, we have simply aimed to focus on the uniaxial compressive strength and compressive deformation of the self-mated fluorinated diamond system based on first-principles calculations. The compressive deformations of the self-mated fluorinated diamond system along the 〈111〉 direction were calculated. The atomic compressive strength of the self-mated fluorinated diamond system should have a significant effect on the tribological behavior of self-mated fluorinated amorphous carbon films.

The study is organized as follows. The calculated method is illustrated in Section 2. From Section 3.1 to 3.3, we describe the compressive stress and strain properties, strain energy and band gap, and total and difference charge of the self-mated fluorinated diamond system, respectively. In Section 4, we discuss the results obtained from Section 3. The main conclusions are listed in Section 5.

2. Calculated method

First-principles calculations were carried out with CASTEP code based on density function theory.¹⁶ The exchange–correlation function was selected as the local density approximation (LDA-CAPZ), and the ultrasoft pseudopotential with cutoff energy of 350 eV was used. The self-mated diamond systems were observed from top- and side-views and are presented in Fig. 1. For the 〈111〉 direction, as reported by Luo,¹⁷ there are two different types of C–C bonds under compressive deformation (denoted as type 1). One type is similar to that found in the 〈111〉 direction, and the other type is perpendicular to the direction of compressive stress (denoted as type 2). The 1 × 1 × 1 unit cell was selected for compressive deformations in the 〈111〉 direction. According to the Monkhorst–Pack scheme, k point grids of 5 × 5 × 1 were used. The methods of compressive strength were similar to our previous study.¹⁷ At each compressive step, a fixed compressive stain was applied in the 〈111〉 direction, and then the lattice parameters were relaxed when the stress tensors orthogonal to the applied stress were less than 0.02 GPa. According to this method, the compressive stresses corresponding to the incrementally applied compressive strains could be calculated.

Fig. 1 Self-mated diamond system model used in the first-principles calculations. (a) Side view of the system. (b) Top view of the system.

3. Results

3.1 Compressive stress and strain properties

We have calculated the compressive stress–strain relationship of the self-mated fluorinated diamond system in the 〈111〉 direction, as shown in Fig. 2. Here, we probe the data point in the stress–strain curve corresponding to the first minimum bond length in compression as a characteristic point. For the compressive deformation along the selected direction, an almost linear proportionality up to around 12% compressive strain was observed, as shown in Fig. 2a. According to the fixed slope of the stress–strain curve, the present deformation can be treated as an elastic deformation.¹⁷ The calculated compressive elastic modulus in this regime was 1856.8 GPa, which is higher than that of the calculated Young's modulus of diamond (1063.0 GPa). The limit compressive strength of −284.4 GPa along the 〈111〉 direction could be obtained with a compressive strain of −0.14. Next, the bond lengths versus strain curve are presented in Fig. 2b–d. For the C–F bond length, as shown in Fig. 2b, the C–F bond length initially decreases and then increases under compressive deformation. A local minimum of 1.306 Å, with the corresponding stress of −284.4 GPa and strain of −0.14, could be observed under compressive deformation. For the C–C bond of type 1, as presented in Fig. 2c, the C–C bond length slightly decreases in the range of strains from 0 to −0.12. In addition, a local minimum compressive bond length of 1.515 Å corresponds to the stress of −222.8 GPa and strain of −0.12. It is worth to note that the local minimum of C–C bond length does not correspond to the limit compressive strength of the system. For the C–C bond of type 2, as shown in Fig. 2d, the C–C bond length monotonically decreases in response to compressive strain. Moreover, one particular bond length of 1.439 Å could be observed in Fig. 2d.

Fig. 2 Calculated stress–strain curve and bond length versus strain for the self-mated fluorinated diamond system along the 〈111〉 direction. For an explanation of the different subpanels, dashed lines, and slope, please refer to the text.

3.2 Strain energy and band gap

As shown in Fig. 3a, the strain energy in response to compressive strain was a monotonic curve. The strain energy initially monotonically increases until a strain of −0.14 and then monotonically decreases. In addition, the difference in the derivative of strain energy with strain is also presented in Fig. 3a. Two critical strain values were deduced. The derivative curve achieves a minimum value at the minimum value of ∈_C1, which indicates that the system can be compressed under smaller compression for high values of strain. For the second point, ∈_C2, represents the yielding point. Exceeding this point, plastic deformation occurs in the system.^18,19 Moreover, the system was actually in a metastable state in the range of strain from ∈_C1 to ∈_C2. The plastic deformations are delayed in this region.

Fig. 3 (a) Variation of strain energy and its first derivative with respect to compressive strain. The region marked with a red dashed line indicates the plastic range. Two critical strains in the elastic range are labeled in the figure. (b) Variation of the band gaps with strain.

In general, apart from phonon instability occurring at a high strain value, the band gap was strongly affected under uniform compression.¹⁸ In Fig. 3b, we show the variation of the band gaps under compressive deformation. The gap slightly increases until a strain of −0.06 and then intermittently decreases with increasing strain. Interestingly, more important information could be obtained from Fig. 3b, which showed that the system transfers from a semiconductor to conductor material.

3.3 Total and difference charge

The total charge (ρ_T) and difference charge (Δρ) of the system were investigated in detail, as shown in Fig. 4. The two fluorinated diamond interfaces were stable until a stain of −0.12. That is, the anti-bonding repulsive forces could withstand a maximum compressive strength of −222.8 GPa. When the system was in the metastable and plastic regimes, the two fluorinated diamond interfaces become unstable. Ultimately, the two fluorinated diamond interfaces disappear under the plastic deformation region. The anti-bonding repulsive force loses the capacity to maintain low friction.

Fig. 4 The total charge density (ρ_T) and difference in charge density (Δρ) of the self-mated fluorinated diamond system. The region marked with a red dashed line is the ρ_T and Δρ at the interface of the self-mated fluorinated diamond system.

4. Discussion

The tribological performance of the carbon films can be significantly affected by the bonding patterns, as reported by Sen et al.²⁰ They also pointed out that fluorinated carbon films exhibit a lower friction coefficient than that found for the hydrogenated films. In addition, Bai et al.^7,9 declared that the anti-bonding repulsive forces played an important role in maintaining a low friction coefficient for fluorinated carbon films based on tight-binding quantum chemical molecular dynamics simulations. Moreover, they also investigated the tribological behavior of fluorinated carbon films under variable contact pressure (1, 3 and 7 GPa). These results were in good agreement with our recent investigation based on the first principles method. In addition, the elastic and plastic deformations that significantly affect the tribological behavior should be considered, as declared by most previous work.^15,21,22 In Fig. 2, the C–F bonds soften until a compressive strain of −0.14. The C–C bond lengths (type 1) remain constant until a compressive strain of −0.12, whereas the C–C bond lengths (type 2) decrease with increasing compressive strain. The results show that the C–C bonds have an effect on resisting the compressive stain in the elastic deformation regions, rather in the plastic deformation regions. Subsequently, the analysis of the total charge (ρ_T) and difference charge (Δρ) of the system (Fig. 4) indicates that a stable fluorinated diamond interface exists until a compressive strain of −0.12. The dislocation of these two interfaces occurs at a compressive strain of −0.14. Moreover, the C–C bond networks remain intact until −0.14. Thus, the intact C–C bonding networks are conducive to maintaining the stable fluorinated diamond interfaces under compressive strain. When the compressive strain exceeds a value of −0.12, the anti-bonding forces gradually lose its capacity for maintaining low friction coefficient. In addition, He et al. have shown that a high value of the band gap in the DLC film was conducive for obtaining low friction when compared to a low value band gap.²³ Thus, the change of band gap (Fig. 3b) of the system can affect the tribological properties of the system.

5. Conclusions

The uniaxial compressive deformation of a self-mated diamond system along the 〈111〉 direction has been investigated based on the first-principles methods. The results show that the calculated limit compressive strength is −284.4 GPa. The system transfers from a semiconductor to conductor with increasing compressive strain. The two fluorinated diamond interfaces are stable until a strain of −0.12 corresponding to a maximum compressive strength of −222.8 GPa. When the compressive strength exceeds this value, these interfaces become unstable.

Acknowledgements

The work was supported by the National Nature Science Foundation of China (Grant 51322508 and 11172300) and Nature Science Foundation of Gansu Province of China (Grant 145RJDA329).

Notes and references

1. A. Erdemir, The role of hydrogen in tribological properties of diamond-like carbon films, Surf. Coat. Technol., 2001, 146, 292–297.
2. K. Yamamoto and K. Matsukado, Effect of hydrogenated DLC coating hardness on the tribological properties under water lubrication, Tribol. Int., 2006, 39, 1609–1614.
3. H. I. Kim, J. R. Lince, O. L. Eryilmaz and A. Erdemir, Environmental Effects on the Friction of Hydrogenated DLC Films, Tribol. Lett., 2006, 21, 51–56.
4. S. Gayathri, N. Kumar, R. Krishnan, T. R. Ravindran, S. Dash, A. K. Tyagi, B. Raj and M. Sridharan, Tribological properties of pulsed laser deposited DLC/TM (TM = Cr, Ag, Ti and Ni) multilayers, Tribol. Int., 2012, 53, 87–97.
5. J. Choi, S. Nakao, S. Miyagawa, M. Ikeyama and Y. Miyagawa, The effects of Si incorporation on the thermal and tribological properties of DLC films deposited by PBII&D with bipolar pulses, Surf. Coat. Technol., 2007, 201, 8357–8361.
6. J. Fontaine, J. L. Loubet, T. Mogne Le and A. Grill, Superlow friction of diamond-like carbon films: A relation to viscoplastic properties, Tribol. Lett., 2004, 17, 709–714.
7. S. Bai, T. Onodera, R. Nagumo, R. Miura, A. Suzuki, H. Tsuboi, N. Hatakeyama, H. Takaba, M. Kubo and A. Miyamoto, Friction reduction mechanism of hydrogen- and fluorine-terminated diamond-like carbon films investigated by molecular dynamics and quantum chemical calculation, J. Phys. Chem. C, 2012, 116, 12559–12565.
8. F. G. Sen, Y. Qi and A. T. Alpas, Surface stability and electronic structure of hydrogen- and fluorine-terminated diamond surfaces: A first-principles investigation, J. Mater. Res., 2009, 24, 2461–2470.
9. S. Bai, H. Murabayashi, Y. Kobayashi, Y. Higuchi, N. Ozawa, K. Adachi, J. M. Martin and M. Kubo, Tight-binding quantum chemical molecular dynamics simulations of the low friction mechanism of fluorine-terminated diamond-like carbon films, RSC Adv., 2014, 4, 33739–33748.
10. G. Levita, A. Cavaleiro, E. Molinari, T. Polcar and M. C. Righi, Sliding properties of MoS₂ layers: load and interlayer orientation effects, J. Phys. Chem. C, 2014, 118, 13809.
11. Y. Qi, E. Konca and A. T. Alpas, Atmospheric effects on the adhesion and friction between non-hydrogenated diamond-like carbon (DLC) coating and aluminum—A first principles investigation, Surf. Sci., 2006, 600, 2955–2965.
12. Y. Qi and L. G. Hector, Adhesion and adhesive transfer at aluminum/diamond interfaces: A first-principles study, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 235401.
13. S. Dag and S. Ciraci, Atomic scale of superlow friction between hydrogenated diamond surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 241401.
14. G. Zilibotti and M. C. Righi, Ab intio calculation of the adhesion and ideal shear strength of planar diamond interfaces with different atomic structure and hydrogen coverage, Langmuir, 2011, 27, 6862–6867.
15. R. H. Zhang, L. P. Wang and Z. B. Lu, Probing the intrinsic failure mechanism of fluorinated amorphous carbon film based on the first-principles calculations, Sci. Rep., 2015, 5, 9419.
16. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, First-principles simulation: ideas, illustrations and the CASTEP code, J. Phys.: Condens. Matter, 2002, 14, 2717.
17. X. G. Luo, Z. Y. Liu, B. Xu, D. L. Yu, Y. J. Tian, H. T. Wang and J. L. He, Compressive strength of diamond from first-principles calculation, J. Phys. Chem. C, 2010, 114, 17851–17853.
18. H. Sahin, M. Topsakal and S. Ciraci, Structure of fluorinated graphenes and their signatures, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 115432.
19. M. Topsakal, S. Cahangirov and S. Ciraci, The response of mechanical and electronic properties of graphane to the elastic strain, Appl. Phys. Lett., 2010, 96, 091912.
20. F. G. Sen, Y. Qi and A. T. Alpas, Material transfer mechanisms between aluminum and fluorinated carbon interfaces, Acta Mater., 2011, 59, 2601–2614.
21. J. Zhang, P. Yan, H. M. Liu and Y. F. Liu, Influence of normal load, sliding speed and ambient temperature on wear resistance of ZG₄₂CrMo, J. Iron Steel Res. Int., 2012, 19, 69–74.
22. I. L. Singer, R. N. Bolster, J. Wegand and S. Fayeulle, Hertzian stress contribution to low friction behavior of thin MoS₂ coatings, Appl. Phys. Lett., 1990, 57, 995–997.
23. X. M. He, K. C. Walter, M. Nastasi, S. T. Lee and X. S. Sun, Optical and tribological properties of diamond-like carbon films synthesized by plasma immersion ion processing, Thin Solid Films, 1999, 355–356, 167–173.

---