Evolution of boron clusters in iron tetraborides under high pressure: semiconducting and ferromagnetic superhard materials

Abstract

We investigated the high-pressure structures and properties of iron tetraborides (FeB₄) using a combination of an ab initio high-throughput search and a particle-swarm optimization algorithm for crystal structure prediction. We found that, under compression, the boron sublattice in FeB₄ from the buckled boron layer first polymerizes into B₄ tetrahedral clusters and then forms cubo-octahedral B₁₂ clusters. At 55 GPa, the orthorhombic crystal structure with a Pnnm space group (58-FeB₄) transforms into a tetragonal I4₁/acd structure (142-FeB₄), which is stable within a wide pressure range up to 695 GPa. Then, a cubic Im3̄m phase (229-FeB₄) emerges at higher pressures up to at least 1 TPa. The computed Vicker's hardnesses of 58-, 142-, and 229-FeB₄ are 61.58, 47.44, and 50.87 GPa, respectively. All of them can be considered as superhard materials. Compared to the previously reported 58-FeB₄ as a superhard superconductor, the B₄ tetrahedral cluster-based 142-FeB₄ is a superhard semiconductor with an indirect band gap of 1.34 eV. The pressure-induced metal-to-semiconductor transition can be related to a unique Fe–B–B three-center covalent bond. Moreover, 229-FeB₄, which is composed of cubo-octahedral B₁₂ clusters, is ferromagnetic with a magnetic moment of 0.929μ_B per Fe atom at ambient pressure. The magnetic moment will decrease rapidly with increasing pressure and be completely quenched as pressure exceeds 40 GPa. The pressure-induced evolution of boron cluster units not only adds new features to boron chemistry, but also gives rise to novel superhard semiconductors or ferromagnetic materials. Moreover, our results may inspire further experimental and theoretical interest in designing new materials using clusters as pseudo-atoms with expected properties.

---

I. Introduction

Boron is an intriguing element due to its exotic bonding nature (e.g., three-center bond and electron deficiency), which leads to the formation of various clusters in elementary boron and in many boron-rich compounds.^1–5 For example, the B₁₂-based icosahedron as the most common structural unit exists in all 16 bulk allotropes of boron and also dominates the structural chemistry of the borides and boride carbides of the main group elements (e.g. BeB₃, LiB₁₂C₁₂, LiB₁₃C₂, and Li₂B₁₂Si₂).¹ Octahedral clusters are present in the tetraborides of several transition metals, including lanthanides, actinides and magnesium as well as CaB_4−xC_x.² Pentagonal, bipyramidal clusters accompanied with octahedral clusters have been identified in Na₃B₂₀.³ Dodecahedral and double-capped square antiprismatic clusters are found in the three-dimensional boron framework of Li₃B₁₄.⁴ In addition, SiB₆, CaB₆, and Li₂B₆ have also been proposed to contain cubo-octahedral clusters.^1,5 The experimental or theoretical discoveries of icosahedral, pentagonal bipyramidal, dodecahedral, double capped square antiprismatic, and octahedral clusters not only enrich the structural chemistry, but also provide new building blocks as pseudo-atoms to design novel materials.⁶

Among many classes of boron solid compounds formed by boron clusters, metal borides have been intensely studied owing to their rich structural characteristics and attractive physical properties. For example, MgB₂ with a simple hexagonal crystal structure, containing graphite-type boron layers separated by hexagonal close-packed layers of Mg atoms, is a premier phonon-coupled superconductor with a high superconducting transition temperature (39 K).⁷ Another interesting class is the hexaborides, MB₆ (M = Ca, Sr, Ba, Na, and K), formed by vertex-linked B₆ octahedra that enclose the metal ion in the cubic interstitial site. Such a bonding state of metal borides always brings about very peculiar properties, e.g., unusual magnetic ordering, heavy fermion formation, good thermionic emission and superconductivity.^8–11 About a decade ago, CaB₄ was synthesized,¹² which contains a three-dimensional network built up from B₆ octahedra and B₂ dumbbells. Band structure calculations indicated that CaB₄ is a stable semiconductor with a narrow band gap, while measurement of its magnetic susceptibility revealed temperature-independent paramagnetism down to 20 K. In addition, the electronic structures of YbB₆, based on B₆ octahedral clusters, and YbB₁₂, based on B₁₂ cubo-octahedral clusters, have been studied by Weng et al.¹³ Their results verified that YbB₆ is a non-trivial Z2 topological insulator and YbB₁₂ is a trivial Kondo insulator. The basic structural unit of metal borides with higher boron concentrations (such as AlB₁₂, AlMgB₁₄, TbB₅₀, and YB₆₆)^14–18 is the B₁₂ icosahedron, which is also present in elementary boron solids.^19,20 Originating from the B₁₂ icosahedra, these crystals usually possess low density, high hardness and high thermal stability, making them promising refractory and superhard materials for use in cutting tools and wear-resistant coatings. More recently, theoretically predicted orthorhombic iron tetraborides FeB₄ (ref. 21) have been successfully synthesized by Gou et al.²² under high pressures (above 8 GPa) and high temperatures (1523–2023 K); these are isostructural to CrB₄ and contain unique corrugated B₆ rings. They found that FeB₄ is highly incompressible with a nanoindentation hardness of 65 GPa and has potential for phonon-mediated superconductivity with T_c = 2.9 K.

The rich physical properties displayed by these metal borides suggest a sensitivity to the detailed geometries of boron clusters as well as their electronic states and bonding nature. In order to elucidate the diversity of boron clusters and their roles in determining the physical properties of metal borides, particularly the mechanical, electronic and magnetic properties, we perform a systematical first-principles investigation of the FeB₄ solid as a prototype and use high pressure as a tool to tune its bonding nature and atomic structure. With increasing pressure, the major building block of the FeB₄ compound transforms from a corrugated B₆ ring to an unusual B₄ tetrahedron and finally to a cubo-octahedral B₁₂ cluster. The latter two boron clusters have never been observed in metal tetraborides and thus add new features to boron chemistry. These novel cluster-based iron tetraborides are distinguished by their unique bonding state and electronic structures and are predicted to be superhard semiconductors or superhard magnetic materials. Our theoretical results indicate that high pressure is a powerful tool to trigger the structural evolution of boron clusters in metal borides and open a new pathway to design material with desirable properties using clusters as pseudo-atoms.

II. Methods

A high-throughput structural search method coupled with a variable-cell particle-swarm optimization algorithm (CALYPSO code²³) was applied to identify the stable structures of FeB₄. Several known polymorphous metal tetraborides from previous studies were reexamined in the FeB₄ system, including orthorhombic oP10-FeB₄ (no. 58, Pnnm, Z = 2),²¹ hexagonal hP20-WB₄ type (no. 194, P6₃/mmc, Z = 4),²⁴ orthorhombic oI10-CrB₄ type (no. 71, Immm, Z = 2),²⁵ orthorhombic OsB₄ (no. 59, Pmmn, Z = 2),²⁶ and hexagonal RuB₄ (no. 194, P6₃/mmc, Z = 2),²⁷ which are denoted hereinafter as 58-, hp20-, 71-, 59-, 194-FeB₄, respectively. Particle-swarm optimization algorithm searches were done in the range of 0–1 TPa with 1, 2, 3, and 4 formula units per simulation cell.

The equilibrium structures of all considered FeB₄ compounds were optimized using spin-polarized density functional theory (DFT), which was implemented in the VASP code.²⁸ The exchange–correlation interaction was treated by the generalized gradient approximation with the Perdew–Burke–Ernzerhof (PBE) functional.²⁹ We employed the projected augmented wave (PAW) method³⁰ by treating 3p⁶3d⁷4s¹ and 2s²2p¹ as valence electrons for Fe and B atoms, respectively. A cutoff energy of 700 eV for the planewave expansion and a k-point grid of uniform spacing of 2π × 0.025 Å⁻¹ were adopted. For all equilibrium crystal structure, phonon dispersion curves were computed using the direct supercell method as implemented in the Phonopy program.³¹ Elastic constants were calculated by the strain–stress method, and bulk modulus and shear modulus were thus derived from the elastic constants using the Voigt–Reuss–Hill averaging scheme.³² The hardness of the crystals was evaluated with Šimůnek's formula using bond strength and atomic density as inputs.³³

III. Results and discussion

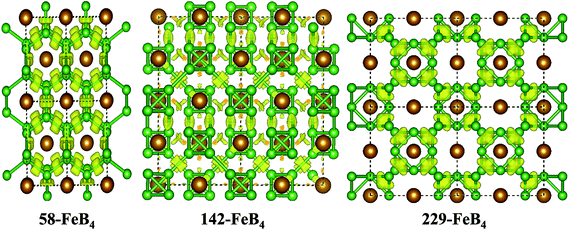
From the particle-swarm searches, we find several new energetically favorable crystalline phases of FeB₄, including two cubic, Im3̄m (no. 229) and F4̄3m (no. 216), one orthorhombic Pbca (no. 64), one hexagonal P6̄m2 (no. 187), and two tetragonal, P4₂/nmc (no. 137) and I4₁/acd (no. 142). Their crystal structures are displayed in Fig. 1. The FeB₄ phases with P4₂/nmc and I4₁/acd space groups have also recently been found by Wang et al.³⁴ and Kotmool et al.,³⁵ respectively. Previous experimental and theoretical results obtained metal tetraborides for 58-, hp20-, 71-, 59-, and 194-FeB₄; these are also shown in Fig. 1 for comparison.^{21,25–27,36} The lattice parameters, cell volumes and total energies per formula unit for all the structures considered, i.e., 58-, 229-, 59-, 187-, 142-, 137-, 64-, 216-, hp20- and 194-FeB₄, are listed in Table 1. At ambient pressure, the experimentally synthesized 58-FeB₄ is still energetically more favorable than the other FeB₄ phases. Moreover, the present lattice parameters and cell volumes for the 58-FeB₄ phases are in excellent agreement with previous experimental²² and theoretical values,^21,37 validating our methodology of DFT calculations.

Fig. 1 The top view and side view of phases 58-, 142-, 229-FeB₄, and some new metastable phases (59-, 187-, 64-, 216-, hp20-, 137-, and 194-FeB₄) are considered here. The blue and pink balls represent Fe and B atoms, respectively.

Table 1 The calculated equilibrium lattice, atomic position, equilibrium volume per molecular chemical formula, total energy per molecular chemical formula, EOS fitted bulk modulus B, and its pressure derivation B′ for phases 58-, 137-, 229-FeB₄, and some new metastable phases (59-, 187-, 64-, 216-, hp20- and 194-FeB₄) are considered here

	Lattice parameters (Å)	Atomic position	V0 (Å^3 per unit)	Etot (eV per unit)	B (GPa)	B′	Hv (GPa)
194	2.876, 2.876, 9.984	B 4f (1/3, 2/3, 0.5436)	35.91	−35.93	263.56	3.79	61.38
		B 4f (1/3, 2/3, 0.1262)
		Fe 2d (2/3, 1/3, 0.25)
58	4.355, 5.211, 2.913	B 4g (0.251, 0.31, 0.5)	36.138	−36.044	259.95	3.77	64.09
		B 4g (0.3393, 0.1232, 1)
		Fe 2b (0, 0, 0.5)
58-expt.^22	4.579, 5.298, 2.999	B 4g (0.249, 0.312, 0.5)	36.376	—	252	3.5	65(5)
		B 4g (0.3411, 0.1263, 1)
		Fe 2b (0, 0, 0.5)
58-theo.^21	4.521, 5.284, 3.006	B 4g (0.2121, 0.341, 0.5)	35.905	—	—	—	—
		B 4g (0.3212, 0.1267, 1)
		Fe 2b (0, 0, 0.5)
229	5.73, 5.73, 5.73	B 24h (0, 0.7831, 0.7831)	34.439	−34.432	270.507	3.92	50.87
		Fe 6b (0 0 0)
59	6.671, 2.794, 3.816	B 4f (0.2045, 0, 0.3313)	35.588	−35.807	275.92	3.79	68.36
		B 4f (0.3577, 0, 0.9835)
		Fe 2b (0, 0.5, 0.5)
hp20	5.128, 5.128, 6.579	B 12i (1/3, 0, 0)	36.74	−33.88	215.84	3.96	34.65
		B 4f (1/3, 2/3, 0.6215)
		Fe 2b (0, 0, 0.25)
		Fe 2c (1/3, 2/3, 0.25)
216	5.048, 5.048, 5.048	B 16e (0.1231, 0.6231, 0.8769)	35.193	−35.563	293.52	3.80	38.80
		Fe 4a (0, 0, 0)
187	3.689, 3.689, 8.828	B 6n (0.4981, 0.9962, 0.1613)	34.885	−34.855	289.74	3.81	31.28
		B 3k (0.1568, 0.3135, 0.5)
		B 2h (0.3333, 0.6667, 0.3328)
		B 1e (0.6667, 0.3333, 0)
		Fe 2i (0.667, 0.3333, 0.6395)
		Fe 1a (0, 0, 0)
137	3.63, 3.63, 5.13	B 8g (0.5, 0.7496, 0.6275)	33.955	−35.518	311.695	3.81	66.74
		Fe 2b (0.5, 0.5, 0)
142	5.136, 5.136, 10.242	B 32g (0.876, 0.37, 0.688)	33.769	−35.524	310.515	3.83	47.44
		Fe 8b (0, 0, 0.25)
64	5.301, 5.264, 5.216	B 16g (0.8415, 0.3595, −0.3939)	36.39	−35.568	255.76	3.89	45.96
		Fe 4b (0.5, 0.5, 0)

---

We further assess the dynamic and mechanical stabilities of these FeB₄ phases in terms of the phonon dispersion and elastic constants. As shown in Fig. 2 and Table 2, there are no negative frequencies throughout the entire Brillouin zone except for 71-FeB₄, and all independent elastic constants satisfy the well-known Born stability criteria.³⁸ These results confirm that the previously reported 58-, hp20-, 59-, and 194-FeB₄ phases and the newly-found 229-, 216-, 64-, 142-, 137-, and 187-FeB₄ phases are dynamically and mechanically stable at ambient conditions.

Fig. 2 Phonon spectra of phases 58-, 142-, 229-FeB₄, and some new metastable phases (59-, 187-, 64-, 216-, hp20-, 137-, and 194-FeB₄) are considered here.

Table 2 Independent elastic constants, bulk, shear, and Young's moduli (all in GPa) and Poisson's ratios of stable phases of 58-, 137-, 229-FeB₄, and some new metastable phases (59-, 187-, 64-, 216-, hp20- and 194-FeB₄) are considered here

No. of space groups	P	C11	C22	C33	C44	C55	C66	C12	C13	C23	B	G	E	υ
58	0	399	719	451	228	226	150	185	172	166	283	184	453	0.23
Expt.^22	0	—	—	—	—	—	—	—	—	—	253	177	431	0.22
Theo.^42	0	408	754	448	229	219	141	165	160	154	277	186	456	0.23
Theo.^43	0	379	761	466	233	226	152	144	143	136	263	194	467	0.20
216	0	696	—	—	246	—	—	102	—	—	300	265	615	0.16
187	0	554	—	633	173	—	188	178	138	—	295	191	471	0.23
137	0	667	—	771	130	—	385	246	47	—	309	248	588	0.18
229	0	559	—	—	84	—	112	—	—	—	261	126	325	0.29
59	0	673	508	596	203	162	347	112	193	82	279	227	536	0.18
64	0	969	578	498	119	151	129	59	102	73	270	183	449	0.22
194	0	452	—	829	209	—	144	164	127	—	278	193	470	0.22
hp20	0	491	—	173	57	—	155	181	107	—	187	92	238	0.29
142	0	637	—	614	313	—	255	188	122	—	305	278	639	0.15
142	400	2412	—	2370	446	—	570	363	440	—	1152	473	1248	0.32
229	1000	2214	—	—	1195	—	—	2140	—	—	1534	1213	2881	0.41

---

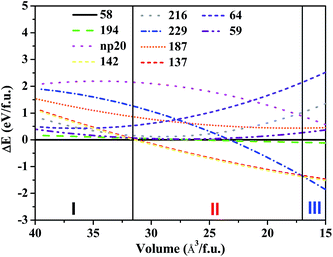
We now compare the total energy of the above candidate structures of FeB₄ per molecular chemical formula under high pressures up to 1 TPa, which can determine the thermodynamically stable high-pressure phase at zero temperature. Fig. 3 shows the energy differences of the static lattices of hp20-, 59-, 194-, 229-, 216-, 64-, 187-, 137-, and 142-FeB₄, relative to the 58-FeB₄ phase as reference. Under compression, the orthorhombic 58-FeB₄ structure (I) remains the most stable phase up to 55 GPa. Then, a tetragonal 142-FeB₄ phase (II) takes over in the pressure range from 55 to 695 GPa, followed by a cubic 229-FeB₄ phase (III) at higher pressures above 695 GPa. Our energy vs. volume curves rule out the other competitive low-enthalpy phases considered here, including hp20-, 59-, 194-, 216-, 64-, 137-, and 187-FeB₄. The transformation pressure between the 58-FeB₄ and the 142-FeB₄ phases is in good agreement with the experiment reported by Gou et al.²² That is, no phase transition of FeB₄ was observed under compression at ambient temperature in a diamond anvil cell up to about 40 GPa.²² Our results are also comparable to a previous theoretical result published by Kotmool et al.,³⁵ who found that the transition between FeB₄ with Pnnm and I4₁/acd phases occurs at 53.7 GPa.

Fig. 3 The relative energy per molecular chemical formula as a function of volume for the competing FeB₄ structures is considered here. Both curves showed that the phase transition sequence is from the Pnnm structure (58-FeB₄) to the tetragonal I4₁/acd structure (142-FeB₄) to the cubic Im3̄m phase (229-FeB₄).

In addition, we have observed two metastable phases in E–V curves, namely, 194-FeB₄ and 59-FeB₄, both of which have comparable enthalpies with the 58-FeB₄ structure, within a broad pressure range. Moreover, note that the 137-FeB₄ phase is slightly less stable than 142-FeB₄ by only 0.03 eV/f.u. within the entire pressure range. Under pressure, it becomes more favorable than 58-FeB₄ beyond 60.5 GPa, which is higher than the transition pressure of 55 GPa for 137-FeB₄. Therefore, the 137-FeB₄ can be considered as a competing metastable phase resulting from compression of 58-FeB₄.³⁴ It is worthy to mention that 58-FeB₄, 194-FeB₄ and 59-FeB₄ have similar layered structures. In addition, 137-FeB₄ and 142-FeB₄ also have similar B₄ tetrahedron-based configurations. These results clearly suggest the correlation between boron frameworks and stability, as well as physical properties, which we will discuss later.

The structural parameters, atomic position and detailed configurations of the 58-FeB₄, 142-FeB₄ and 229-FeB₄ phases in their stable pressure ranges are now carefully examined and shown in Table 1 and Fig. 4. For 58-FeB₄, the equilibrium lattice constants at zero GPa are: a = 4.355 Å, b = 5.211 Å, and c = 2.913 Å. In this structure, two iron atoms sit in the Wyckoff 2b site (0, 0, 0.5) and eight boron atoms occupy two inequivalent 4g sites [(0.25, 0.31, 0.5) and (0.34, 0.13, 0)]; hence, the boron atoms constitute a buckled layer with a graphene-like honeycomb network, centered by Fe atoms along the z direction. The equilibrium lattice constants of the 142-FeB₄ phase at 400 GPa are as follows: a = 4.354 Å and c = 8.702 Å. The structure is a combination of two interpenetrating tetragonal sublattices, displaced along the body diagonal of the tetragonal cell by a 1/2 length. Thus, the eight Fe atoms hold the Wyckoff 8b sites (0, 0, 1/4) and thirty-two B atoms occupy the 32g site (0.88, 037, 0.69). More interestingly, the 32 boron atoms are polymerized into eight B₄ tetrahedral clusters (Fig. 1). All the boron tetrahedral clusters are covalently linked by B–B bonds, while each Fe atom is surrounded by six B₄ clusters. For the 229-FeB₄ phase, high-symmetry cubic structures with 6 formulas per unit cell are found. Its equilibrium lattice parameter at 1000 GPa is a = 4.542 Å. Six Fe atoms exist in the 6b sites (0, 0, 0) and 24 boron atoms lie in the 24h sites (0, 0.78, 0.78). Structurally, this phase can be regarded as a cubo-octahedral B₁₂-based binary metal compound, in which two cubo-octahedral B₁₂ clusters form a body-centered cubic (BCC) sublattice with six Fe atoms centered on the face and edge. In brief, our theoretical simulations show the evolution of a boron framework in FeB₄ solids, along with a pressure-induced phase transition, that is, the buckled layer of boron atoms in iron tetraborides is first polymerized into a square array of B₄ tetrahedral clusters and then condensed into cubo-octahedral B₁₂ clusters spatially arranged in a BCC lattice.

Fig. 4 The electronic localization function (ELF) of 58-FeB₄, 142-FeB₄, and 229-FeB₄ under 0 GPa. The big and small balls represent iron and boron atoms, respectively. The buckled layer boron structure, the B₄ tetrahedral cluster, and the cubooctahedral B₁₂ cluster are observed for 58-, 142-, and 229-FeB₄ structures, respectively.

The low enthalpy structures of CaB₆ under pressure revealed the rebonding pathways of its covalent network.³⁹ The known ground state of CaB₆ under zero pressure is cP7, which is constructed from boron octahedra. The competing high-pressure structures of CaB₆ include oP28, oS28, oS56, and tI56. oP28 is one of possible distorted cP7, which is made out of boron octahedral. oS28 is constructed from twinned pentagonal bipyramids. In oS56, half of the boron octahedra are opened up to form a zigzag strip, while four boron octahedra are fused into interconnected 24-atom units to form tI56. In addition, carbon, the neighbor of boron in the periodic table, has exhibited similar pressure-induced cluster evolution phenomena. Li et al.⁴⁰ found that the polymeric anions of metal carbides (Li₂C₂ and Ca₂C₂) at high pressure showed significant evolution from C₂ dumbbells to chains to layers and then to strands, and part of them are predicted to be pressure-induced superconductors. It is also noteworthy that both the tetrahedral B₄ and cubooctahedral B₁₂ clusters are not typical building units for metal borides. To date, cubooctahedral structures for B₁₂ clusters have only been found in a few compounds with high boron concentrations, such as YbB₁₂,¹³ ZrB₁₂,⁴¹ and ScB₁₂,⁴¹ which have considerably higher boron contents than FeB₄. Moreover, the B₄ tetrahedral clusters in the metal borides differ distinctly from the rhomboidal and rectangular B₄ units in 58-FeB₄ (ref. 21 and 22) and 71-FeB₄.²⁵ The evolution of boron clusters under pressure shown here not only adds a new feature to boron chemistry, but also suggests that the compressed FeB₄ solids might present some novel physical properties.

To explore the potential applications of these iron tetraborides with novel cluster-based structures, we first investigate the mechanical properties of 58-, 142-, and 229-FeB₄ as well as the other stable metastable FeB₄ phases considered here. As shown in Table 2, our calculated elastic constants for 58-FeB₄ are comparable to previous theoretical values^21,42,43 and experimental values.²² At zero pressure, all the abovementioned crystal structures of FeB₄ have large values of C₁₁, C₂₂, and C₃₃, indicating that they are extremely difficult to compress along the a, b, and c axes. From the calculated elastic constants, the bulk modulus, the shear modulus, and the Young's modulus are thus evaluated and given in Table 2. One can observe that 58- and 142-FeB₄ have comparable bulk modulus (about 300 GPa), close to the experimental value for WB₄ (304 GPa).⁴⁴ Moreover, the shear modulus and the Young's modulus of 142-FeB₄ are 278 and 639 GPa, respectively, and both are higher than those of 58-FeB₄ (184 GPa and 453 GPa). For 229-FeB₄, its bulk modulus, shear modulus, and Young's modulus are 261, 126, and 375 GPa, respectively, which are slightly lower than those of the 58-FeB₄ and 229-FeB₄ phases. Using Šimůnek's method,³³ we further predict the Vicker's hardnesses of these FeB₄ systems. The hardness of 58-FeB₄ from our calculation is 64.09 GPa, which is consistent with experimental value of 65(5) GPa.²² At ambient pressure, the predicted hardnesses are 47.44 GPa for 142-FeB₄ and 50.87 GPa for 229-FeB₄. In short, our theoretical results for both elastic modulus and hardness⁴⁵ suggest that 142-FeB₄ and 229-FeB₄ are potential superhard materials like 58-FeB₄. We have to mention that there is a big controversy on the hardness of the 58-FeB₄. The experimental results have recently been challenged in a theoretical study.^37,42,46

The elastic constants and elastic modulus of 142-FeB₄ under 400 GPa and of 229-FeB₄ under 1000 GPa are also shown in Table 2. One can see that both these values increase monotonically with increasing pressure. For example, for 142-FeB₄, the bulk modulus, shear modulus, and Young's modulus are 1152, 473, and 1248 GPa at a high pressure of 400 GPa, and at zero pressure the corresponding values are 305, 278, and 639 GPa. Moreover, the hardnesses of 142-FeB₄ and 229-FeB₄ also increase to 76.64 GPa and 86.39 GPa under 400 GPa and 1000 GPa, respectively. Thus, we conclude that 142-FeB₄ and 229-FeB₄ are expected to be superhard materials, not only under ambient pressure, but also in their stable pressure ranges.

To explain the origin of high hardness and to gain more insight into the bonding character and charge transfer between metal ions and boron clusters, we calculate the electron localization function (ELF) and the Mulliken charge. Generally speaking, the ELF helps us to understand the localized bonding in real space of the crystal and can be used to distinguish between metallic, covalent and ionic bonding. By definition, ELF = 1 means perfect electron localization. The bonding characters of 58-FeB₄, 142-FeB₄ and 229-FeB₄ are well supported by the ELF picture. The strong localization between B atoms in buckled layers of boron atoms corresponds to the 2-center 2-electron (2c2e) bond for 58-FeB₄. In addition, cubo-octahedral B₁₂ clusters of 229-FeB₄ exhibit 3-center 2-electron (3c2e) bonding, which is found in the B₁₂ icosahedra because of the electron deficient nature of the B atoms.⁴⁷ More interestingly, we found that the valence electrons of 142-FeB₄ mainly locate at the B–B bond and the Fe–B–B triangle, forming the conventional two-center and the novel three-center bonds. To further explain such three-center Fe–B–B polar covalent bonds, we count the electrons in 142-FeB₄. According to Wade's rule,⁴⁸ a tetrahedral cluster with four vertices needs 2 × 4 + 2 = 10 electrons to stabilize the polycentric bonding system. Moreover, each tetrahedron forms four 2e2c B–B bonds with the neighboring B₄ tetrahedrons; thus, four electrons are required for each B₄ unit. Altogether, to stabilize such a tetrahedral B₄ cluster, 10 + 4 = 14 electrons per formula unit are required. However, four boron atoms only have 12 valence electrons in total. These missing two electrons are expected to be supplied by Fe atoms. However, according to our Mulliken population analysis, the number of electrons transferred from Fe to B atoms is 1.03e. This suggests that Fe–B bonds are half ionic and half covalent.

The ELF isosurfaces and the 2D profiles of 58-, 142-, and 229-FeB₄ at ambient pressure are displayed in Fig. 5 and 6. Note that again a higher value of the ELF corresponds to higher electron localization. Strong covalent B–B bonds can be inferred because the maximal ELF values between two neighboring boron atoms are 0.72, 0.66, and 0.65 for 58-, 142-, and 229-FeB₄, respectively. The ELF backgrounds between two bonded iron and boron atoms are 0.41, 0.57, and 0.43, which also manifest the partial covalent interaction between Fe and B atoms that is considerably weaker than B–B bonds. Moreover, the region around the B atom has an overall higher ELF value than the region of the Fe atom, reflecting the partial iconicity of Fe–B bonding with charge being transferred from Fe to B. According to the Mulliken population analysis, the on-site charges of the B atom are −0.4e, −0.33e, and −0.27e for 58-, 142-, and 229-FeB₄, respectively, under ambient pressure. That is to say, every buckled boron layer of 58-FeB₄ gains 1.6 electrons, each B₄ tetrahedral cluster of 142-FeB₄ gains 1.32e, and each cubo-octahedral B₁₂ cluster of 229-FeB₄ gains 3.24e. The abovementioned analysis of charge transfer and ELF clearly indicates that B–B bonds and Fe–B bonds are driving forces for the high hardness of FeB₄ compounds.

Fig. 5 The ELF profiles from a B atom to the nearest B atom and from a Fe atom to the nearest B atom for the 58-, 137-, and 229-FeB₄ phases at ambient pressure.

Fig. 6 Partial density of states of 142-FeB₄ phases at ambient pressure. The black vertical dotted line indicates the Fermi level.

The unique bonding states revealed above motivate us to investigate their corresponding electronic properties. Generally speaking, metal borides usually possess good electrical conductivity. For example, 58-FeB₄ was predicted to be metallic with a high density of state (DOS) at the Fermi level.^21,22 Indeed, the 229-FeB₄ phase is also metallic with a DOS at the Fermi level that is ten times higher than 58-FeB₄. To our surprise, we find that the B₄ tetrahedron-based 142-FeB₄ crystal opens an indirect gap of 1.34 eV (at the PBE level), which is shown in Fig. 6 and 7. This is really rare for metal borides. Such results mean that a metal to semiconductor transformation will occur in the FeB₄ system under compression. In the DOS of 142-FeB₄ (Fig. 6), the B p and Fe d orbitals show strong hybridization near the Fermi level. Again, this corresponds to the Fe–B covalent bonds, which has already been demonstrated by our ELF isosurface of 142-FeB₄ (Fig. 9). A large portion of electrons are distributed on the Fe–B–B plane. In other words, the Fe and B atoms of 142-FeB₄ share electrons like boron atoms and behave as three-center polar covalent bonds, which are responsible for its semiconductor characteristics.

Fig. 7 Band structures of 142-FeB₄ phases under 0 GPa, 100 GPa, 400 GPa, and 800 GPa. The red vertical dotted line indicates the Fermi level. The corresponding band gaps are 1.34 eV, 1.50 eV, 1.36 eV and 1.07 eV.

Fig. 8 The band gap and the Fe charge of 142-FeB₄ phases with respect to pressure up to 1000 GPa.

Fig. 9 The electronic localization function (ELF) of 142-FeB₄ under 0 GPa, 100 GPa, 400 GPa, and 800 GPa. The big and small balls represent iron and boron atoms, respectively. The electrons of 142-FeB₄ under 0 GPa and 100 GPa are mainly located at the B–B bond or the Fe–B–B triangle, forming the common two-center or unique three-center bonds. The electrons of 142-FeB₄ under 400 GPa and 800 GPa are located at the center of the B–B bond or the tetrahedron, forming the common two-center or unique four center bonds.

Under high pressure, the variation of band structures can be divided into two parts (Fig. 8). Below 100 GPa, the band gap initially increases. After that, the band gap reduces. Up to 1000 GPa, the band gap declines to ∼0.9 eV, indicating a trend towards metallization. We display the band structures of the 142-FeB₄ phase under 0 GPa, 100 GPa, 400 GPa, and 800 GPa in Fig. 7. Although they are all indirect band gap semiconductors, an amazing transition tendency from indirect to direct band gap is found, driven by the pressure induced increasing valence band offset.

To further explore the pressure effect on band gap, we plot the ELF isosurface of 142-FeB₄ under 0 GPa, 100 GPa, 400 GPa and 800 GPa, as shown in Fig. 9. As stated above, the electrons are mainly located in the center of the B–B bonds and the Fe–B–B plane at 0 GPa. With increasing pressure, the electron localization around the Fe–B–B triangle is significantly diminished. As the pressure approaches 400 GPa or higher (800 GPa), the ELF at the Fe sites is nearly negligible, whereas it reaches local maximum values at the center of the B₄ tetrahedral cluster. Therefore, we conclude that one effect of pressure is to drive the electron distribution from the Fe atoms toward to the B atoms gradually, which in turn has a significant influence on the bonding states of the FeB₄ phases. That is, two-center B–B bonds and three-center Fe–B–B polar covalent bonds of 142-FeB₄ at ambient pressure will transform into B–B bonds, four-center B₄ tetrahedral covalent bonds, and Fe–B metallic bonds. Mulliken population analysis also reveals the pressure-induced charge transfer of 142-FeB₄ phases. The average number of electrons transferred from Fe to B atoms are 1.32e, 1.81e, and 2.56e under 0 GPa, 100 GPa and 400 GPa, respectively.

The shortening of interatomic distances is another effect of pressure, which leads to band gap variation in 142-FeB₄. When the pressure is less than 100 GPa, pressure induced bonding states are dominant and thus the band gaps are widened. Above 100 GPa, the pressure-induced shrinking of bond lengths is more pronounced. Mulliken population analysis (Fig. 8) shows that the electron transfer from Fe to B atoms under compression first increases significantly and then starts to decrease. For example, the amplitude of electron transfer is 2.4e under 800 GPa, which is rather close to that of 2.56e under 400 GPa. Moreover, the average bond length of B–B (Fe–B) is shortened from 1.82 Å (1.90 Å) to 1.44 Å (1.608 Å) over the entire pressure range with a compression rate of 0.0038 Å GPa⁻¹ (0.0029 Å GPa⁻¹). This will lead to an increasing overlap of valence and conduction bands owing to the Fe–B and B–B interaction. As a consequence, the band gap will decrease.

Due to the partial filling of narrow 3d bands and the high DOS near the Fermi level of the pure Fe solid, it would be interesting to investigate the magnetic properties of Fe-based compounds to understand the nature of their ferromagnetism. From our spin-polarized calculations, we find a ferromagnetic 229-FeB₄; every Fe atom possesses a magnetic moment of 0.929μ_B under 0 GPa, which is substantially lower than that of the pure Fe solid (2.2μ_B). In contrast, the 58-FeB₄ and 142-FeB₄ phases are nonmagnetic. Fig. 10 shows the dependence of the magnetic moment of 229-FeB₄ on pressure, illustrating that the magnetic moment decreases rapidly with increasing pressure. Up to 40 GPa, the magnetic ordering is almost completely quenched. Previous studies have also revealed that the spin state of metallic iron exhibits remarkable pressure dependence. Based on X-ray magnetic circular dichroism measurements, Iota et al.⁴⁹ have shown that the net magnetic moment in Fe vanishes above 18 GPa. Such interesting pressure-induced change of spin state within 229-FeB₄ can be understood by the peculiar interaction between Fe and B atoms. For 229-FeB₄, the magnetic moment is determined by the relation between ionic and covalent bonding, both of which are sensitive to pressure simply related to the shortening of interatomic distance under compression. For example, the B–B and the Fe–B bonds exhibit lengths of 1.794 Å and 1.90 Å at 0 GPa. Up to 1000 GPa, the bond lengths decrease to 1.448 Å and 1.613 Å. Accordingly, the relative reduction of the ionic contribution to Fe–B bonding leads to a slight decrease in the number of unpaired electrons accumulated on the Fe atoms, thus giving rise to variations in the magnetic moment of FeB₄ under pressure. Geest et al.⁵⁰ have also found the magnetic moment per atom of metal borides as a function of the metal–metal distance and composition, which further supports our present results.

Fig. 10 The magnetic moment per iron atom as a function of pressure for 229-FeB₄.

IV. Conclusion

The structures and the dynamic, mechanical, electronic and magnetic properties of FeB₄ solids under high pressure up to 1 TPa were systematically explored using first-principles calculations. The pressure-induced transformations from 58-FeB₄ to 142-FeB₄ and to 229-FeB₄ were predicted and a large number of metastable phases were identified using the particle-swarm optimization algorithm. The phonon dispersion and elastic constants calculations have demonstrated their dynamic and mechanical stability. Under high pressure, the boron atoms from the buckled layer of boron atoms in iron tetraborides initially polymerize into square arrays of B₄ tetrahedral clusters and then further transform into cubo-octahedral B₁₂ clusters. To the best of our knowledge, neither of these boron cluster units are typical structural motifs for metal borides.

Originating from their unique boron cluster-based structures, the FeB₄ solids at ambient and high pressures present some novel mechanical, electronic and magnetic properties. First, 58-, 142-, and 229-FeB₄ are superhard materials with considerable Vickers hardnesses of 64.09 GPa, 47.44 GPa and 50.87 GPa, respectively. According to charge transfer and ELF analysis, the B–B and Fe–B bonds are the driving forces for such high hardnesses. The geometric and electronic characteristics of buckled layers of boron atoms, B₄ tetrahedral clusters and B₁₂ cubo-octahedral clusters in 58-, 142-, and 229-FeB₄ mainly account for the excellent material strength. Second, unlike typical metallic borides, the B₄ tetrahedral cluster-based 142-FeB₄ is a semiconductor. Fe–B–B three-center polar covalent bonds and B–B two center covalent bonds are responsible for this unusual electronic behavior. The pressure-induced band gap variation of 142-FeB₄ is simultaneously determined by the charge transfer and the reduction of interatomic distance. Third, we have demonstrated that only the cubo-octahedral B₁₂ cluster-based 229-FeB₄ exhibits magnetic ordering within three stable high pressure FeB₄ phases. The competition between ionic bonding and covalent bonding interactions under pressure is thought to be the main reason behind this fascinating phenomenon.

The formation of B₄ tetrahedral and cubo-octahedral B₁₂ clusters in Fe–B solids from our theoretical simulations demonstrate that pressure is a powerful tool to trigger different novel boron clusters, which certainly enrich the boron chemistry. The pressure-induced metal-to-semiconductor and ferromagnetic-to-paramagnetic phase transitions might be observed in other materials as well, providing a new idea for designing novel materials using clusters as pseudo-atoms with desirable properties.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (11134005 and 11404050), China Postdoctoral Science Foundation (no. 2014M551065) and the Fundamental Research Funds for the Central Universities of China (no. DUT14RC(3)041).

References

1. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
2. R. Schmitt, B. Blaschkowski, K. Eichele and H. J. Meyer, Inorg. Chem., 2006, 45, 3067–3073.
3. B. Albert, Angew. Chem., Int. Ed., 1998, 37, 1117–1118.
4. G. Mair, R. Nesper and H. G. von Schnering, J. Solid State Chem., 1988, 75, 30–40.
5. J. Hoard, R. Hughes and E. Muetterties, The chemistry of boron and its compounds, Wiley, New York, 1967, p. 59.
6. M. Okamoto, K. Hashimoto and K. Takayanagi, Appl. Phys. Lett., 1997, 70, 978–980.
7. J. Nagamatsu, N. Nakagawa, T. Muranaka, Y. Zenitani and J. Akimitsu, Nature, 2001, 410, 63–64.
8. D. Hall, D. Young, Z. Fisk, T. Murphy, E. Palm, A. Teklu and R. Goodrich, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 233105.
9. R. Monnier and B. Delley, Phys. Rev. Lett., 2001, 87, 157204.
10. K. Schmitt, C. Stückl, H. Ripplinger and B. Albert, Solid State Sci., 2001, 3, 321–327.
11. H. Tromp, P. Van Gelderen, P. Kelly, G. Brocks and P. Bobbert, Phys. Rev. Lett., 2001, 87, 016401.
12. R. Schmitt, B. Blaschkowski, K. Eichele and H.-J. Meyer, Inorg. Chem., 2006, 45, 3067–3073.
13. H. Weng, J. Zhao, Z. Wang, Z. Fang and X. Dai, Phys. Rev. Lett., 2014, 112, 016403.
14. B. A. Cook, J. L. Harringa, T. L. Lewis and A. M. Russell, Scr. Mater., 2000, 42, 597–602.
15. T. Mori, J. Appl. Phys., 2004, 95, 7204–7206.
16. S. M. Richards and J. Kaspar, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1969, 25, 237–251.
17. I. Higashi, J. Solid State Chem., 2000, 154, 168–176.
18. X. Jiang, J. Zhao, A. Wu, Y. Bai and X. Jiang, J. Phys.: Condens. Matter, 2010, 22, 315503.
19. J. Donohue, Structures of the Elements, 1974.
20. J. Zhao and J. P. Lu, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 092101.
21. A. Kolmogorov, S. Shah, E. Margine, A. Bialon, T. Hammerschmidt and R. Drautz, Phys. Rev. Lett., 2010, 105, 217003.
22. H. Gou, N. Dubrovinskaia, E. Bykova, A. A. Tsirlin, D. Kasinathan, W. Schnelle, A. Richter, M. Merlini, M. Hanfland and A. M. Abakumov, Phys. Rev. Lett., 2013, 111, 157002.
23. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
24. P. Romans and M. Krug, Acta Crystallogr., 1966, 20, 313–315.
25. H. Niu, J. Wang, X.-Q. Chen, D. Li, Y. Li, P. Lazar, R. Podloucky and A. N. Kolmogorov, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 144116.
26. M. Zhang, H. Yan, G. Zhang and H. Wang, J. Phys. Chem. C, 2012, 116, 4293–4297.
27. Y. Wang, T. Yao, L.-M. Wang, J. Yao, H. Li, J. Zhang and H. Gou, Dalton Trans., 2013, 7041–7050.
28. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
29. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
30. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
31. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
32. R. Hill, Proc. Phys. Soc., London, Sect. A, 1952, 65, 349.
33. A. Šimůnek and J. Vackář, Phys. Rev. Lett., 2006, 96, 085501.
34. Q. Wang, Q. Zhang, M. Hu, M. Ma, B. Xu and J. He, Phys. Chem. Chem. Phys., 2014, 16, 22008–22013.
35. K. Kotmool, T. Kaewmaraya, S. Chakraborty, J. Anversa, T. Bovornratanaraks, W. Luo, H. Gou, P. C. Piquini, T. W. Kang and H.-K. Mao, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17050–17053.
36. B. Wang, D. Y. Wang and Y. X. Wang, J. Alloys Compd., 2013, 573, 20–26.
37. M. Zhang, M. Lu, Y. Du, L. Gao, C. Lu and H. Liu, J. Chem. Phys., 2014, 140, 174505.
38. Z.-J. Wu, E.-J. Zhao, H.-P. Xiang, X.-F. Hao, X.-J. Liu and J. Meng, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054115.
39. A. N. Kolmogorov, S. Shah, E. R. Margine, A. K. Kleppe and A. P. Jephcoat, Phys. Rev. Lett., 2012, 109, 075501.
40. D. Benson, Y. Li, W. Luo, R. Ahuja, G. Svensson and U. Häussermann, Inorg. Chem., 2013, 52, 6402–6406.
41. K. Hamada, M. Wakata, N. Sugii, K. Matsuura, K. Kubo and H. Yamauchi, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 6892.
42. X. Zhang, J. Qin, J. Ning, X. Sun, X. Li, M. Ma and R. Liu, J. Appl. Phys., 2013, 114, 183517.
43. L.-P. Ding, X.-Y. Kuang, P. Shao and X.-F. Huang, Inorg. Chem., 2014, 53, 3471–3479.
44. Q. Gu, G. Krauss and W. Steurer, Adv. Mater., 2008, 20, 3620–3626.
45. C.-M. Sung and M. Sung, Mater. Chem. Phys., 1996, 43, 1–18.
46. B. Li, H. Sun and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 014106.
47. B. Decker and J. Kasper, Acta Crystallogr., 1959, 12, 503–506.
48. K. Wade, Inorg. Nucl. Chem. Lett., 1972, 8, 559–562.
49. V. Iota, J.-H. P. Klepeis, C.-S. Yoo, J. Lang, D. Haskel and G. Srajer, Appl. Phys. Lett., 2007, 90, 042505.
50. A. Van Der Geest and A. Kolmogorov, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2014, 46, 184–204.

---