Structural and dielectric anomalies near the MPB region of Na_0.5Bi_0.5TiO₃–SrTiO₃ solid solution

Abstract

In the present attempt, (1 − x)NBT(Na_0.5Bi_0.5TiO₃)–xST(SrTiO₃) (x = 0.24–0.28) solid solutions are studied near the MPB region to investigate short-range structural and dielectric anomalies. X-ray diffraction study confirms the presence of MPB by the co-existence of rhombohedral (202), (122) and pseudocubic (002), (112) peaks at x = 0.25–0.26. For x = 0.24, the absence of pseudocubic peaks indicate the complete diffusion of cubic ST phase into the rhombohedral phase of pure NBT. RAMAN spectra exhibit the appearance of new vibrational modes at A and B sites by the splitting of bands in the NBT–ST at the MPB (x = 0.25–0.26), which are not detected for x < 0.25 and x > 0.26. This can be assigned to local ordering at the A-site cations (Bi/Na/Sr) and B-site TiO₆ octahedral distortion, respectively. The high-temperature RAMAN spectra confirm the structural stability at up to 550 °C of all NBT–ST samples near the MPB. Dielectric transition temperature is shifted from 360 °C to 160 °C with ST and shows a single broad anomaly. The broadening of the dielectric peak with deviation from Curie–Weiss law proves the dielectric dispersion near the MPB region of NBT–ST. The MPB origin is the outcome of local imbalance due to chemical inhomogeneity at the A site and short-range disordering at the B site. This induces strain-charge disparity, which influences dielectric behavior.

---

I. Introduction

Na_0.5Bi_0.5TiO₃ (NBT) is a perovskite-based complex ferroelectric material that exhibits morphotropic phase boundary (MPB) with the other perovskites such as BaTiO₃ (BT), SrTiO₃ (ST), etc. Currently, NBT-based perovskites have been intensively focused on as a next-generation, environmentally friendly, lead-free piezoelectric material. Despite five decades of discovery of NBT and its derivatives, there is a lack of clarity on certain crucial issues, such as structural complexity, various aspects of atomic displacements, and respective lattice distortions and their role in MPB. Basically, NBT has a rhombohedral perovskite structure with R3c symmetry by polar cation displacements and antiphase rotations of the oxygen octahedral.¹ The fundamental interest on the NBT-based solid solution is the mixed-valency ions of very different electronic structures (e.g. Bi³⁺, Na⁺, Sr²⁺, Ba²⁺) sharing the A site in perovskite. The local interactions among them during accommodation at the A sites give rise to a series of concentration- and temperature-driven phase transitions.² NBT has been found to exhibit different temperature-driven phases, such as rhombohedral, tetragonal and cubic with an intermediate mixed phase between rhombohedral–tetragonal.³ Concentration-dependent structural transition of NBT-based solid solutions is also very interesting. The room temperature phase diagram of (1 − x)Na_0.5Bi_0.5TiO₃–xBaTiO₃ [NBT–BT] shows structural phase transition from rhombohedral to tetragonal with the existence of rhombohedral–tetragonal MPB at x = 0.06.⁴ In comparison, (1 − x)Na_0.5Bi_0.5TiO₃–xSrTiO₃ [NBT–ST] rhombohedral-to-cubic phase transition has been observed with increasing Sr concentration with rhombohedral–cubic MPB.^5–8 The exact concentration of ST in NBT is not clear. The role of BT or ST, specially A-site ions in the formation of MPB in NBT, needs to be closely monitored to understand the origin. The exact location of MPB, the role of different ions at the A and B sites, local disorder and lattice displacement in most of the solid solution are inconclusive.^5–8

There are many recent attempts to probe structural anomalies in NBT-based materials near the MPB. Gorfman et al. have studied the low symmetry phase in the NaBiTiO₃ crystal by using optical birefringence microscopy and predicted that below 573 K, NaBiTiO₃ sustains a monoclinic structure instead of rhombohedral.⁹ Trujillo et al. have observed pressure-induced phase transition in the NBT-based system (Na_0.5Bi_0.5)_0.89Ba_0.11TiO₃ by using RAMAN spectroscopy and found phase transition in the sequence tetragonal → rhombohedral → cubic with increasing pressure.¹⁰ Rout et al. have detected MPB in Ba-doped Na_0.5Bi_0.5TiO₃ by using high-temperature RAMAN and X-ray techniques.¹¹

The dielectric behaviour of NBT-based systems has been found very sensitive to temperature and dopant level. The first dielectric anomaly was reported at ∼220 °C, named ‘T_d’ to represent the ferroelectric-to-antiferroelectric phase transition. A second dielectric anomaly has been observed at ∼320 °C, abbreviated as ‘T_m’ corresponding with rhombohedral-to-tetragonal structural transition.^12–14 Many research efforts tried to correlate structural transition and dielectric anomaly.^15–18 In order to understand the phase transition anomalies in this system, solid solutions such as 0.94Na_0.5Bi_0.5TiO₃–0.06BaTiO₃,¹⁹ Na_0.5Bi_0.5TiO₃–Bi_0.5Li_0.5TiO₃, Na_0.5Bi_0.5TiO₃–Bi_0.5K_0.5TiO₃,²⁰ Na_0.5Bi_0.5TiO₃–CaTiO₃,²¹ (NaK)_0.5Bi_0.5TiO₃,²² Na_0.5Bi_0.5TiO₃–K_0.5Na_0.5NbO₃,²³ Na_0.5Bi_0.5TiO₃–BaTiO₃–K_0.5Na_0.5NbO₃,²⁴ Na_0.5Bi_0.5TiO₃–SrTiO₃,²⁵ etc. have been developed. Formation of the MPB in NBT-based solid solutions is found responsible for tuning the phase transition and enhanced electromechanical properties.

To understand the origin of the MPB, chemical homogeneity and respective short-range structural changes near the MPB needs to be monitored closely. RAMAN spectroscopy is widely used to probe the short-range structural changes.^24,26,27 Despite many studies, several important questions, such as (i) A-site atomic ordering for different cations and their influences on association with B and O ions and (ii) the effect of the local interaction on symmetry and structural changes, still need to be enlightened.

In the present attempt, nanosized NBT–ST solid solutions at composition x = 0–0.30 were synthesized by using a novel hydrothermal combustion route. The compositions of ST(x) were finely varied by 0.01 intervals to exactly locate ST content at the MPB. To our knowledge, this is the first attempt to prepare fine-scale NBT–ST by this synthesis route. X-ray diffraction (XRD) data were used to confirm the pure crystalline phase structure of the NBT–ST solid solution. The composition and temperature-dependent, short-range structural transition and dielectric behavior were closely monitored near the MPB. Local structural disorderings were studied by Raman spectroscopy. The existence of MPBs was confirmed by the development of new shoulders in XRD peaks, which outset at x = 0.25 and disappear at 0.27 onwards. This clearly indicates that below this composition, the material well exhibits rhombohedral symmetry and above it transforms to pseudocubic structure. RAMAN spectra show additional vibrational modes: (i) at the A site by splitting of the broad band around 100 cm⁻¹, associated to Bi–O, Sr–O, and Na–O respectively; (ii) at the B site by splitting of the band around ∼276 cm⁻¹ related to TiO₆ octahedral distortion at the MPB region (x = 0.25–0.26) in the NBT–ST solid solution. A small shoulder is observed around 670 cm⁻¹ corresponding with the Ti–O stretching mode, which is found to disappear at x = 0.27 onwards; and (iii) high-temperature Raman spectroscopy exhibits anomalous vibrational modes at the B-site around 140 °C. These can be associated to dielectric transition, which is around ∼160 °C and related to antiferroelectric-to-paraelectric phase transition. The dielectric transition temperature was reduced from 320 °C to 160 °C.

II. Experimental procedure

In the present work, we have synthesized the (1 − x) NBT–xST (x = 0, 0.24, 0.25, 0.26, 0.27, 0.28) solid solutions by using a novel hydrothermal combustion method. The precursors were taken in the form of nitrate. Bismuth nitrate (BiNO₃·5H₂O, Sigma-Aldrich), sodium nitrate (NaNO₃, Merck), strontium nitrate (SrNO₃, Sigma-Aldrich), and titanium isopropoxide (Ti(OC₃H₇)₄, Across) were used as starting precursors. Nitric acid (HNO₃) was used as solvent, and liquor ammonia (NH₄OH) was used to adjust the pH of the solution. Citric acid was used as a chelating agent as well as fuel for the combustion method. The synthesis was carried out in two steps. First, a separate solution of titanium isopropoxide was prepared in citric acid with 1 : 2 molar ratio of metal cation to citric acid. The pH of the solution was adjusted to ∼6 by adding liquor ammonia dropwise. Then, the stoichiometric amount of titanium isopropoxide was added and stirred at 80 °C for 2 hours. Secondly, all the metal nitrates were dissolved in nitric acid. Then, citric acid was added to make a 1 : 2 molar ratio of metal to citric acid. Liquor ammonia was added to maintain the pH of the solution at ∼6. After that, the titanium solution was added, and the total solution was stirred for 20 minutes at room temperature. The solution was then transferred to a Teflon-lined steel autoclave with 300 ml capacity. The autoclave was placed in a hot air oven at 120 °C for 30 hours. Then, the autoclave was allowed to cool naturally. The resulting solution was transferred to a glass beaker and heated at 220 °C in an open muffle furnace. This process led to evaporation followed by exothermic chemical reactions that resulted in the production of flames. The resulting powder was calcined at 700 °C for 3 hours in a programmable closed muffle furnace with a heating rate of 5 °C minute⁻¹ to obtain a well crystallized NBT–ST powder. The resulting powder was ground in an agate mortar, with the addition of 2% polyvinyl alcohol as a binder. The powder was poured in a 9 mm steel die punch to form a pellet under 7 MPa pressure for 15 minutes in a hydraulic press. The pellets were sintered in a programmable muffle furnace at different temperatures (800 to 950 °C) for 4 hours to optimize the sinterability. The relative density of all pellets was obtained between 92 to 94%.

The crystal structures of the resulting calcined powder were characterized by X-ray powder diffraction using a D8 Advance Bruker Germany 2.2 KW Cu anode and a ceramic X-ray tube. The data were recorded with a step size of 0.197 and step time of 46.5 ms. Electronic microscope images and EDX of the samples were performed by using JEOL/EO JSM-6380 electron microscope. RAMAN spectra were recorded in the temperature range of 50 °C to 550 °C within the wavenumber range 50 cm⁻¹ to 1000 cm⁻¹ using a Horiba Jobin LABRAM-HR spectrometer in the visible range. The samples were excited by the laser source He–Ne at 632.8 nm and argon at 488 nm. For electrical properties, silver paint was applied on the surface of the pellet. To form a good electrical contact, the pellet was dried at 500 °C for half an hour in a closed muffle furnace. Dielectric measurement in the temperature range 30–500 °C was done on a LCR meter (Waynekerr model 4100) equipped with a programmable box furnace at a heating rate of 2 °C min⁻¹.

III. Result and discussion

A. X-ray diffraction

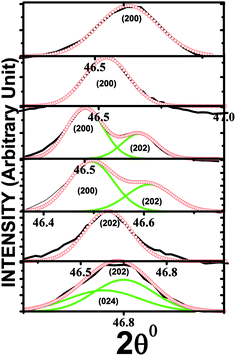
X-ray diffraction patterns of the (1 − x)NBT–xST (x = 0, 0.24–0.28) are shown in Fig. 1(a–c). The XRD data for x = 0.24 are well fitted (see Fig. 2) by Rietveld refinement done by using R3c space group, and with pseudo-Voigt function, confirm the single-phase pure rhombohedral perovskite structure. However, for x = 0.25, an additional shoulder is detected near the peaks 2θ = 46.8 (202) and 2θ = 58.2 (122) and found to be related with the (002) and (112) of cubic phase of NBT. The presence of (202), (002), (122) and (112) peaks represent the co-existence of rhombohedral and pseudocubic phase (Fig. 1b and c). To clarify this observation, the XRD peak at (202) is fitted by Gaussian function (see Fig. 3). It confirms the origin of the shoulder with shifting of the (202) peak towards the higher angular side at x = 0.25. The shoulder peak is related to the (002) pseudocubic phase of NBT–ST. It gives clear evidence for formation of the morphotropic phase boundary, which begins at x = 0.25 and continues to be more prominent for x = 0.26. In comparison, for the composition x = 0.27, the (202) and (122) peaks suddenly disappear, and the structures are found to match the pseudocubic structure. Thus, variations of composition concentration from 0.24 to 0.28 in NBT–ST are found to induce structural transformation from rhombohedral to pseudocubic, mediated by the rhombohedral–pseudocubic MPB. The accompanying lattice parameter shift as a function of ST content was calculated from the diffraction peaks based on the rhombohedral (R3c) space group (shown in the inset of Fig. 1a). The c/a ratio → ∼1 with (x > 0.26) composition is clear evidence for the decrease in rhombohedral phase and emergence of pseudocubic structural transition.

Fig. 1 (a) XRD of NBT–ST at different compositions of ST, (b and c) magnified view of additional peaks.

Fig. 2 Rietveld refinement of the NBT system.

Fig. 3 Gaussian fitting of (202) peak.

Tolerance factor plays a more essential role in the phase transition of the system. Goldsmith tolerance factor^28–30 given by the equation 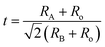where R_A, R_B and R_o are the radii of the A, B and oxygen ions, respectively, is used to explain the structural transformation in perovskite materials. The addition of ST into the NBT slightly increases the tolerance factor of the NBT–ST solid solution because of the larger tolerance factor of ST (1.013) than that of the pure NBT (0.977), which indicates that the rhombohedral structure of the NBT deviates to a more symmetric ideal cubic perovskite at higher ST concentration.

B. Electron microscopy image and EDX result

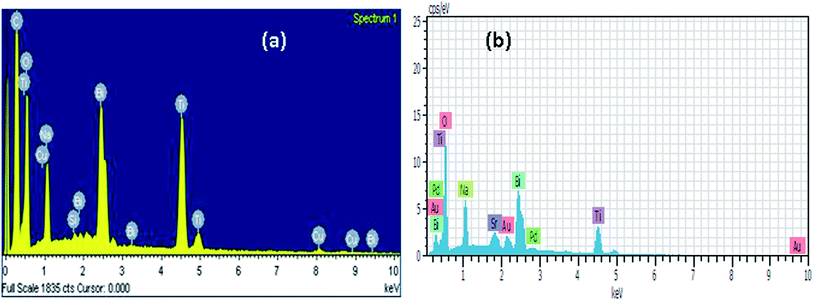
Fig. 4a and b show the electron microscopy image and EDX result of the calcined powders of Bi_0.5Na_0.5TiO₃ and 0.74(Bi_0.5Na_0.5TiO₃)–0.26(SrTiO₃) ceramics, respectively. Both SEM images reveal highly agglomerated, irregularly shaped particles with size below 100 nm. This is always expected in combustion-synthesized samples. The element distributions in NBT and NBT–ST are checked by EDX; see Fig. 5a and b, respectively. EDX results exhibit the existence of all elements with appropriate concentration, except for a slight change in Bi and Na proportion as compared to the expected 1 : 1 stoichiometry. This can be attributed to loss of Bi due to a highly volatile nature. EDX data for both samples are listed in Table 1. The additional elements Cu, Au, Pd are due to coating, Si due to glass substrate, and C due to atmosphere.

Fig. 4 SEM images of (a) pure NBT and (b) 0.74NBT–0.26ST solid solution.

Fig. 5 EDX of (a) pure NBT and (b) 0.74NBT–0.26ST solid solution at room temperature.

Table 1 Elemental distribution of the NBT-based system by EDX

Sr. no.	Bi0.5Na0.5TiO3		0.74(Bi0.5Na0.5TiO3)–0.26(SrTiO3)
	Element	Atomic%	Element	Atomic%
1	Bi	2.38	Bi	6.54
2	Na	3.77	Na	11.11
3	Ti	7.67	Ti	24.63
4	O	34.27	O	54.31
5	Si	0.18	Sr	2.05
6	Cu	2.09	Au	1
7	C	51.02	Pd	0.36

---

C. Raman spectroscopy

Room-temperature RAMAN spectra of the unpoled (1 − x)NBT–xST (x = 0.24–0.28) are studied and displayed in Fig. 6. All the peaks are fitted by Lorentzian function. The outset areas in Fig. 6 show the Lorentzian fitted data for 0.76NBT–0.24ST (sample system). The room-temperature crystal structure of the end members of the NBT–ST solid solution has been reported as rhombohedral R3c for NBT and cubic Pm3̄m for ST. For the composition in the neighborhood of the MPB, generally the presence of both phases has been reported. According to the group theory given by Kreisel et al.,³¹ there are 13 IR and RAMAN (7A1 + 6E) active modes for the BNT R3c structure. The simultaneous IR and RAMAN activity splits each A1 and E mode into their longitudinal and transverse optic modes, so that in principle, 24 modes should be visible in the RAMAN spectra of R3c structure. However, the intensity of some modes is very weak, and in pure NBT, it causes broadening of the neighboring band. Hence, in the RAMAN spectra of pure NBT, 4 broad peaks have been reported by Parija et al.³² These are assigned as: (i) band centered at 146 cm⁻¹ A₁(TO₁) related to the distorted octahedral BiO₆ and NaO₆ cluster, (ii) broad band near 281 cm⁻¹ E(TO₂) due to stretching of short-range TiO₆ octahedral, (iii) band at 542 cm⁻¹ (LO₂) attributed to O–Ti–O stretching symmetric vibration of the TiO₆ cluster, and (iv) broad band centered at 812 cm⁻¹ (LO₃) mode assigned to longitudinal (LO) and transverse (TO) components, which are due to the presence of sites containing octahedral distorted [TiO₆] clusters in the rhombohedral lattice. However, for ST cubic structure, no first-order RAMAN active modes are generally obtained. It shows second-order RAMAN scattering peaks in the room-temperature RAMAN spectrum. Moreover, two peaks in the range 200–500 cm⁻¹ and in between 550–750 cm⁻¹ have been detected in the room-temperature RAMAN spectra of bulk cubic ST.³³

Fig. 6 RAMAN spectra of NBT–ST with different compositions. Outset shows magnified view of RAMAN anomaly.

Our results show the red-shifting in the Raman peaks of NBT–ST, which according to literature can be assigned to the particle size effect. The dominant features of the RAMAN spectra are as follows: (i) peaks are observed near ∼70 cm⁻¹, 110 cm⁻¹, ∼134 cm⁻¹, ∼274 cm⁻¹, and ∼540 cm⁻¹, with a broad and weak band at ∼810 cm⁻¹; (ii) weakening of the mode near 134 cm⁻¹, which completely disappears x = 0.27; (iii) splitting of the mode near 274 cm⁻¹ for x = 0.25 and 0.26; (iv) hardening of the mode near 540 and anomalous at x = 0.25 onwards; (v) weak peak at 620 cm⁻¹, which disappears at x = 0.27 onwards; and (vi) splitting of the mode near 840 cm⁻¹ for x = 0.26. These changes can be seen more clearly in the outset of Fig. 6, determined by fitting the spectra by Lorentzian lines. The splitting of modes and discontinuity in frequency changes at x = 0.25 and 0.26 are evidences of local structural rearrangement.

The vibrational mode near 70 cm⁻¹, 110 cm⁻¹ and 138 cm⁻¹ can be assigned to A-site cation vibrations of the BiO₆, SrO₁₂, and NaO₆ clusters, respectively, in accordance with mass frequency relation. The magnified view of composition-dependent A-site cation vibrations of NBT–ST (Fig. 6) shows that: (i) for x = 0 and x = 0.24, weak A-site modes associated with vibration of BiO₆ and NaO₆ clusters are detected; (ii) for x = 0.25 and 0.26, clear and distinct features of all three A-site vibrational modes are clearly observable and attributed to local ordering of Bi, Na and Sr ions at the A-site; (iii) for x = 0.27 onwards, mode related to the vibration of NaO₆ cluster suddenly disappears, indicating that Na disordering at the A-site may be due to more probable local interaction between Na and Sr, due to close similarity of Na and Sr as Na–O and Sr–O bonds have ionic nature, while Bi–O is highly covalent and Bi is volatile. All these lead to the disordering of Sr/Na at the A site during rearrangement. For x < 0.25, the material shows the rhombohedral phase of NBT. However, for x = 0.25 and 0.26, all local cation ordering leads to the co-existence of rhombohedral–pseudocubic phases. For x = 0.27 onwards, Na disordering at the A site comes up with pseudocubic phase.

A close look at the B site vibrational mode shows that the broad band near 274 cm⁻¹ corresponding with Ti–O vibration in TiO₆ octahedra is split into sharp peaks at the MPB region. However, for x < 0.27, the bands resolved into a single broad peak. The splitting can be assigned to asymmetric vibrations of Ti–O bonds, and thus TiO₆ octahedral distortion induces non-uniform Ti-cation displacements, which are prominent at the MPB region in NBT–ST. Similarly, the mode near 542 cm⁻¹ (Fig. 4) associated with O–Ti–O stretching symmetric vibration of the TiO₆ cluster hardens with rising ST concentration and becomes anomalous at the MPB. A shoulder is detected near 680 cm⁻¹ for x = 0.24 to 0.26, which disappears at x = 0.27 onwards. The broad and weak band centered at the 812 cm⁻¹ (LO₃) mode is commonly associated with distorted sites arising from the presence of the octahedral distorted [TiO₆] clusters in the rhombohedral lattice. The polar character of the lattice classifies this mode into longitudinal (LO) and transverse (TO) components. An anomalous split in the mode is detected at x = 0.26.

All these spectral changes reveal that for ST concentrations x = 0.25 and x = 0.26, ordering of Bi, Na, and ST at the A site is clearly viewed with the sharp splitting of the B-site peak, attributed to structure and symmetry shift at x = 0.25 and x = 0.26. The cation (Bi³⁺/Na⁺/Sr²⁺) ordering at the A site and Ti displacement by TiO₆ octahedral distortion at the B site outset at x = 0.25 are responsible for the co-existence of the rhombohedral–pseudocubic phase at the MPB. The disordering of Na⁺ at the A site and symmetric Ti–O vibration in TiO₆ octahedra at the B site observed at x = 0.27 is due to structural transition from MPB to pseudocubic as replicated by the XRD profile (Fig. 1).

According to symmetry and selection rules of NBT and ST, a gradual change from rhombohedral to cubic can be expected with increasing Sr concentration, which can lead to a decrease in Raman active mode. The existence of almost all Raman modes associated with the rhombohedral phase and XRD peaks matched with the cubic phase for x ≥ 0.27, indicating gradual transition of rhombohedral to pseudocubic through intermediate short-range, non-cubic phases.

The temperature-dependent Raman vibration and respective short-range structural changes of the NBT–ST system near MPB are monitored by high-temperature RAMAN spectroscopy (see Fig. 7). The irreversibility of the local changes is also investigated by studying the spectra during cooling (see Fig. 7). The five different compositions (x = 0.24, 0.25, 0.26, 0.27, 0.28) of the unpoled (1 − x) NBT–xST solid solution very close to the MPB regions are probed in the temperature range 30 °C to 550 °C during the heating and cooling cycle. The temperature-driven spectral anomalies, which are commonly observed in all compositions, include: (i) broadening of mode with reduction of FWHM, (ii) decreased intensity of peaks with rising temperature, and (iii) asymmetric peaks. The trend is reproduced during cooling (see Fig. 7). All these are attributed to temperature-induced local structural disordering and excitation of additional vibrational modes near the local structural heterogeneity, respectively. No prominent vibrational modes are detected in the given temperature range (30–550 °C). However, some new modes at A site and B site are noticed for x = 0.26 and 0.27. These were not reproduced during cooling. The temperature-sensitive Raman vibrations have not shown any bulk structural transition up to 550 °C; this indicates that the MPB region is also sustained up to 550 °C.

Fig. 7 Temperature-dependent RAMAN spectra of the NBT–ST system during heating and cooling cycles.

The origin of MPB lies in the disorder of the Bi³⁺ and Na⁺ due to the insertion of Sr²⁺ ions at the A-site and resultant Ti displacement at the B site in ABO₃ perovskite. The divergent nature Sr–O, Na–O and Bi–O bonds are responsible for inducing A-site local disordering. The Na–O and Sr–O are ionic, and the Bi–O is highly covalent, according to the Pauli scale. The divergence of the bonds is anticipated because of the introduction of positional disorder on the oxygen sublattice. The rise in Sr–O concentration is responsible for the increase in disorder, as O cloud is distributed to form A–O and B–O bonds in ABO₃ perovskite. The A site induces positional distortion in the oxygen sublattice, leading to Ti–O bond deformation, which is accompanied by TiO₆ octahedral distortion and Ti displacement.

D. Dielectric study

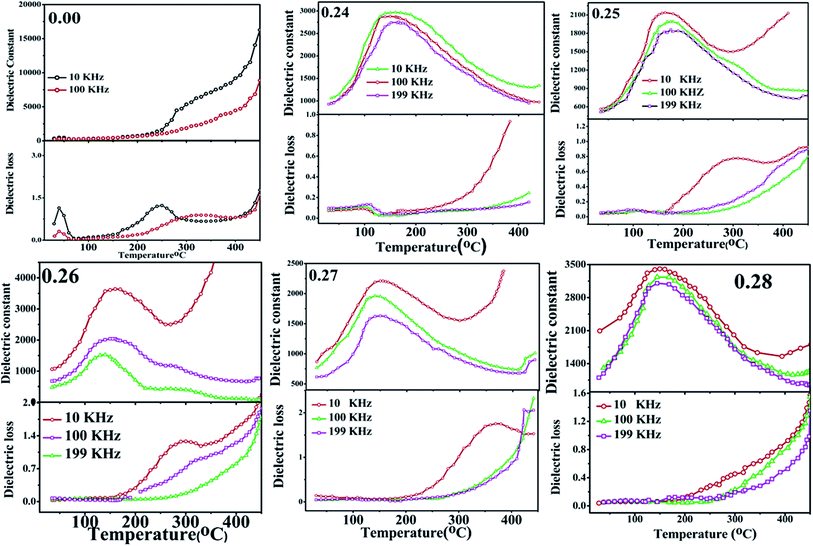
The temperature and frequency dependence of the dielectric behaviour of unpoled (1 − x NBT–xST) sample at 10 kHz, 100 kHz and 199 kHz in the temperature range 30 °C to 400 °C were investigated (see Fig. 8). The dielectric permittivity as a function of temperature (έ–T curve) of pure NBT exhibits anomaly around 320 °C, which can be associated to structural transition from room temperature rhombohedral to tetragonal phase. However, the T_d (depolarization temperature) corresponding to the polar ferroelectric-to-antiferroelectric transition is not detected; it may be suppressed due to the unpoled nature of the sample. Dielectric constant is found to continuously rise with temperature to 550 °C, which is related to tetragonal-to-cubic transition in the case of pure NBT.

Fig. 8 έ–T and tan δ–T curve of the NBT–ST system.

In NBT–ST solid solution near the MPB region, the έ–T curve displays dielectric anomaly at around 160 °C (see Fig. 8). The central broad peak observed for each composition correlates to antiferroelectric (non-centrosymmetric space group: R3c)-to-paraelectric phase transition (non-centrosymmetric space group: P4mm). It is evident that doping induces two major changes in the NBT system: (i) shifting the peak temperature (T_m) to a lower temperature, and (ii) broadening in the dielectric spectra. The lowering of transition temperature with rising ST concentration can be attributed to the increase in isovalency of the NBT–ST solid solution at the A site by partial replacement of (Bi³⁺Na⁺) by Sr²⁺ and the covalency of the A–O bond with fractional replacement of Na–O by Sr–O,²⁵ because the Na–O and Sr–O bonds are ionic in nature, while the Bi–O bond is covalent in nature, as discussed earlier. Thus, the shift in valence state of the A site and covalency of A–O bonds induce polarization anomaly in the structure, which leads to lowering of the transition temperature. Also, it has been observed that ferroelectricity in NBT originating from the lone pair effect of Bi³⁺ and the partial replacement of Sr ²⁺ at the A site could affect the decrease in T_m value.³³

Broadening of the έ–T curve is a consequence of strain and disorder-induced relaxation polarization near the transition temperature. The dispersions in the dielectric can also be explained by the strong heterogeneity induced at the A site due to the partial replacement of Bi³⁺ and Na⁺ by Sr²⁺, which perturbs the coulomb interaction at long range and shows the formation of polar nanodomains. The heterogeneity in the random field lattice may decrease the degree of coupling between permanent dipoles.³⁴ Therefore, the ferroelectric domains are destroyed, and the short-range cation ordering is formed, resulting in a polar nanodomain, which includes the relaxor ferroelectric behavior.³⁵ Frequency dispersion is also detected in the range 10–200 kHz. For three different frequencies (10 kHz, 100 kHz and 199 kHz), έ–T curves are distinguishable and demonstrate a compositionally disordered system, as do relaxors. However, the sample with composition x = 0.24 shows weak frequency dispersion and relaxation before phase transition, as well as lower dielectric loss. For the composition x = 0.26 and 0.27, sudden rise in dielectric loss is observed at around 300 °C. This is attributed to conductance due to mobile charge carriers.

The fall of the dielectric constant after the transition temperature in a typical ferroelectric material generally follows the Curie–Weiss law. This behavior is demonstrated by plotting 1/έ as a function of temperature at constant frequency 100 kHz for different compositions (Fig. 9). The high frequency is chosen to eliminate the effect of interfacial capacitance on the dielectric constant. Deviation from Curie–Weiss law is observed for almost all the samples. The data in the reciprocal dielectric constant graph (1/έ–T) was fitted with a straight line for T > T_m, and the Curie–Weiss temperature (T_CW) was extrapolated from the fitted line. Burn's temperature, T_B, is determined from the 1/έ–T curve. It refers to the temperature below which 1/έ is a non-linear function of T. T_B signifies the cross-line between soft mode and order–disorder dynamics. When the temperature decreases below T_B, polar nanoregions appear, and the displacive-type soft mode is overdamped. The Curie–Weiss law becomes invalid within the temperature range of T_m–T_B. The difference ΔT_m = T_m − T_B is used to estimate deviation of the system from classic Curie–Weiss behavior as has been discussed by K. Datta et al.³⁶ In general, T_B rises with doping concentration. However, in the present attempt, T_B is found to decrease with increasing doping level, suggesting the rise of structural ambiguity near phase transition due to the MPB. Non-zero values of ΔT_m suggest relaxation near phase transition, and it gives rise to the broadening of έ–T. The extent of deviation decreases near the MPB, and it further increases for x ≥ 0.27. For quantitative measurement of diffuseness, the diffusive coefficient (γ) is determined by fitting the data to the modified Curie–Weiss law (given by the equation 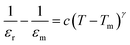). The diffusive coefficient decreases at the MPB region from 1.8 to 1.2 and suddenly rises to 2.01 at x = 0.28 (Fig. 10). Both results clearly indicate that the extent of both relaxation and diffuseness were reduced at the MPB.

Fig. 9 Reciprocal dielectric 1/έ versus temperature curve.

Fig. 10 Modified Currie–Weiss law.

The dielectric constant shows a little independence from frequency at low temperature. But at high temperature, frequency dependence behaviors are observed, with the dielectric constant rapidly decreasing with increasing frequency. The increase in dielectric constant at low frequency and high temperature is attributed to the oxygen vacancy effect, which arises from the pronounced composition fluctuation due to A-site ions (Bi³⁺, Na⁺, Sr²⁺) at high temperature.³⁷

Anomalies in dielectric loss are found near the MPB region; the sample with composition x = 0.24 shows weak frequency dispersion and relaxation before phase transition. However, for x = 0.25 onwards, relaxation is observed around 300 °C. The relaxation anomaly is prominent at 10 kHz frequency, while it disappears with rise in frequency. It is not observed for x = 0.28. This is attributed to conductance due to mobile charge carriers at low frequency and high temperature.

IV. Conclusion

(1 − x)NBT–xST (x = 0–0.30) solid solutions are synthesized by a novel hydrothermal-combustion route. X-ray diffraction study confirms the existence of the MPB (rhombohedral–pseudocubic) by the co-existence of (202), (002), (122) and (112) peaks at x = 0.25–0.26. To investigate dielectric and local structural distortion near MPB in detail, (1 − x)NBT–xST (SrTiO₃) (x = 0.24–0.28) composition studies are performed by dielectric permittivity and RAMAN spectroscopy. XRD confirms the complete diffusion of the cubic phase of ST in NBT with formation of the solid solution. RAMAN spectra exhibit the appearance of new vibration modes at A and B sites by splitting of peaks in NBT–ST at the MPB (x = 0.25–0.26), which was obtained for x < 0.25 and disappeared at x > 0.26 onwards. This indicates short-range ordering of A-site cations (Bi/Na/Sr) and B-site TiO₆ octahedral distortion. Dielectric data as a function of temperature show a lowered dielectric transition temperature from 360 °C to 160 °C near the MPB. The broadening of the dielectric peak with deviation from Curie–Weiss law proves the dielectric dispersion near the MPB region of NBT–ST. The origin of the MPB is the local imbalance due to chemical inhomogeneity and short-range disordering. The induced strain-charge disparity influences dielectric behaviour.

Acknowledgements

S.S. acknowledges UGC New Delhi for providing financial assistance through MANF Fellowship. S.A.A. and P.K. acknowledge the financial support from DST New Delhi, India under project of SR/FTP/PS-106/2009 (G) and UGC under MRP F.N. 41-871/2012.

References

1. I. Levin, I. M. Reaney, E.-M. Anton, W. Jo, J. Rodel, J. Pokorny, L. A. Schmitt, H.-J. Kleebe, M. Hinterstein and J. L. Jones, Local structure, pseudosymmetry, and phase transition in Na_1/2Bi_1/2TiO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 024113,  DOI:10.1103/physrevb.87.024113.
2. D. Xiao, D. Lin, J. Zhu and P. Yu, Investigation on the design and synthesis of new system of BNT-based lead free piezoelectric ceramics, J. Electroceram., 2006, 16, 271,  DOI:10.1007/s10832-006-9863-7.
3. V. Shuvaeva, D. Zekira and A. Glazer, Local structure of the lead free relaxor ferroelectric K_xNa_(1−x)Bi_0.5TiO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 174114,  DOI:10.1103/physrevb.71.174114.
4. T. Takenaka, K. I. Maruyama and K. Sakata, (Bi_1/2Na_1/2)TiO₃–BaTiO₃ System for Lead-Free Piezoelectric Ceramics, J. Jpn. Appl. Phys., 1991, 30, 2236,  DOI:10.1143/jjap.30.2236.
5. Y. Hiruma, Y. Imai, Y. Watanabe, H. Nagata and T. Takenaka, Large electrostrain near the phase transition temperature of (Bi_0.5Na_0.5)TiO₃–SrTiO₃ ferroelectric ceramics, Appl. Phys. Lett., 2008, 92, 262904,  DOI:10.1063/1.2955533.
6. S. Park and K. Hong, Variation of structure and dielectric properties on substituting A-site cations for Sr²⁺ in (Na_1/2Bi_1/2)TiO₃, J. Mater. Res., 1997, 12, 2152,  DOI:10.1557/jmr.1997.0288.
7. T. Wang, H. Du and X. Shi, Dielectric and ferroelectric properties of (1 − x)Na_0.5Bi_0.5TiO₃–xSrTiO₃ lead-free piezoceramic system, J. Phys.: Conf. Ser., 2009, 152, 012065,  DOI:10.1088/1742-6596/152/1/012065.
8. W. Krauss, D. Schutz, F. Mautner, A. Feteira and K. Reichmann, Piezoelectric properties and phase transition temperatures of the solid solution of (1 − x)(Bi_0.5Na_0.5)TiO₃–xSrTiO₃, J. Eur. Ceram. Soc., 2010, 30, 1827,  DOI:10.1016/j.jeurceramsoc.2010.02.001.
9. S. Gorfman, A. Glazer, Y. Noguchi, M. Miyayama, H. Luo and P. Thomas, Observation of a low symmetry phase in Na_0.5 Bi_0.5TiO₃ crystal by optical birefringence microscopy, J. Appl. Crystallogr., 2012, 45, 444,  DOI:10.1107/S0021889812008217.
10. S. Trujillo, J. Kreisel, Q. Jiang, J. Smith, P. Thomas, P. Bouvier and F. Weiss, The high pressure behaviour of Ba-doped investigated by RAMAN spectroscopy, J. Phys.: Condens. Matter, 2005, 17, 6587,  DOI:10.1088/0953-8984/17/41/027.
11. D. Rout, K. Moon, J. Park and S. Kang, High temperature X-ray diffraction and Raman scattering studies, of Ba-doped (Na_0.5Bi_0.5)TiO₃, Curr. Appl. Phys., 2013, 13, 1988,  DOI:10.1016/j.cap.2013.08.016.
12. Y. Li, W. Chen, J. Zhou, Q. Xu, H. Sun and R. Xu, Dielectric and piezoelectric properties of lead-free (Na_0.5Bi_0.5)TiO₃–NaNbO₃ceramics, Mater. Sci. Eng., B, 2004, 112, 5,  DOI:10.1016/j.mseb.2004.04.019.
13. B. N. Rao, R. Dutta, S. S. Chandrashekaran, D. K. Mishra, V. Sathe, A. Senyshen and R. Ranjan, Local structural disorder and its influence on the average global structure and polar properties in Na_0.5Bi_0.5TiO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 224103–224114,  DOI:10.1103/physrevb.88.224103.
14. X. Wang, H. Chan and C. Choy, (Bi_1/2Na_1/2)TiO₃–Ba(Cu_1/2W_1/2)O₃ lead-free piezoelectric ceramics, J. Am. Ceram. Soc., 2003, 86, 1809,  DOI:10.1111/j.1151-2916.2003.tb03562.x.
15. V. Dorcet, G. Trolliard and P. Boullay, The structural origin of the antiferroelectric properties and relaxor behavior of Na_0.5Bi_0.5TiO₃, J. Magn. Magn. Mater., 2009, 321, 1758,  DOI:10.1016/j.jmmm.2009.02.013.
16. E. Aksel, J. Forrester, B. Kowalski, J. Jones and P. Thomes, Phase transition sequence in sodium bismuth titanate observed using high-resolution X-ray diffraction, Appl. Phys. Lett., 2011, 99, 222901,  DOI:10.1063/1.3664393.
17. S. Zhang, A. Kounga, E. Aulbach and Y. Deng, Temperature-Dependent Electrical Properties of 0.94Bi_0.5Na_0.5TiO₃–0.06BaTiO₃ Ceramics, J. Am. Ceram. Soc., 2008, 91, 3950,  DOI:10.1111/j.1551-2916.2008.02778.x.
18. Y. Hiruma, K. Yoshii, H. Nagata and T. Takenaka, Phase transition temperature and electrical properties of Bi_1/2Na_1/2TiO₃–(Bi_1/2A_1/2)TiO₃ (A = Li and K) lead-free ferroelectric ceramics, J. Appl. Phys., 2008, 103, 084121,  DOI:10.1063/1.2903498.
19. R. Ranjan, R. Garg, V. kothai, A. Agrawal, A. Senyshyn and H. Boysen, Phases in the (1 − x)Na_0.5Bi_0.5TiO₃–(x)CaTiO₃ system, J. Phys.: Condens. Matter, 2010, 22, 075901,  DOI:10.1088/0953-8984/22/7/075901.
20. J. Kreisel, A. Glazer, G. Jones, P. Thomas, L. Abello and G. Lucazeau, An X-ray diffraction and Raman spectroscopy investigation of A-site substituted perovskite compounds: the (Na_1−xK_x)_0.5Bi_0.5TiO₃ (0 ≤ x ≤ 1) solid solution, J. Phys.: Condens. Matter, 2000, 12, 3267,  DOI:10.1088/0953-8984/12/14/305.
21. J. Hao, W. Bai, W. Li, B. Shen and J. Zhai, Phase transitions, relaxor behavior, and electrical properties in (1 − x)(Bi_0.5Na_0.5)TiO₃–x(K_0.5Na_0.5)NbO₃ lead-free piezoceramics, J. Mater. Res., 2012, 27, 2943,  DOI:10.1557/jmr.2012.328.
22. F. Gao, X. Dong, C. Mao, H. Zhang, F. Cao and G. Wang, Poling temperature tuned electric-field-induced ferroelectric to antiferroelectric phase transition in 0.89Bi_0.5Na_0.5TiO₃–0.06BaTiO₃–0.05K_0.5Na_0.5NbO₃ ceramics, J. Appl. Phys., 2011, 110, 094109,  DOI:10.1063/1.3660283.
23. K. Sakata and Y. Masuda, Ferroelectric and antiferroelectric properties of (Na_0.5Bi_0.5)TiO₃–SrTiO₃, solid solution ceramics, Ferroelectrics, 1974, 7, 347,  DOI:10.1080/00150197408238042.
24. D. Rout, K. Moon, S. Kang and I. Kim, Dielectric and Raman scattering studies of phase transitions in the (100 − x)Na_0.5Bi_0.5TiO₃–xSrTiO₃ system, J. Appl. Phys., 2010, 108, 84102,  DOI:10.1063/1.349078.
25. P. Jaita, A. Watcharapasorn and S. Jiansirisomboon, Investigation of a new lead-free Bi_0.5(Na_0.40K_0.10)TiO₃–(Ba_0.7Sr_0.3)TiO₃ piezoelectric ceramic, Nanoscale Res. Lett., 2012, 17, 24.
26. X. Wang, S. Choy, X. Tang and H. Chan, Dielectric behavior and microstructure of Bi_1/2Na_1/2TiO₃–Bi_1/2K_1/2TiO₃–BaTiO₃ lead-free piezoelectric ceramics, J. Appl. Phys., 2005, 97, 104101,  DOI:10.1063/1.1890453.
27. M. Yoon, Y. Lee and S. Ur, Effects of co-doped CaO/MnO on the piezoelectric/dielectric properties and phase transition of lead-free (Bi_0.5Na_0.5)_0.94Ba_0.06TiO₃ piezoelectric ceramics, J. Electroceram., 2009, 23, 564,  DOI:10.1007/s10832-008-9548-5.
28. O. Muller and R. Roy, The Major Ternary Structural Families, Springer, New York, 1974, p. 221.
29. F. S. Galasso, Perovskites and High Tc Superconductors, Gordon and Breach, New York, 1990.
30. S. Shanmuga Sundari, B. Kumar and R. Dhanasekaran, Structural, Dielectric, Piezoelectric and Ferroelectric Characterization of NBT–BT Lead-Free Piezoelectric Ceramics, IOP Conf. Ser.: Mater. Sci. Eng., 2013, 43, 012010.
31. J. Kreisel, A. Glazer, G. Jones, P. A. Thomas, L. Abello and G. Lucazeau, An X-ray diffraction and Raman spectroscopy investigation of A-site substituted perovskite compounds the (Na_1−xK_x)_0.5Bi_0.5TiO₃ (0 ≤ x ≤1) solid solution, J. Phys.: Condens. Matter, 2000, 12, 3267,  DOI:10.1088/0953-8984/12/14/305.
32. B. Parija, S. Rout, L. Cavalcante, A. Simoes, S. Panigrahi, E. Longo and N. Batista, Structure, microstructure and dielectric properties of 100 − x(Bi_0.5Na_0.5)TiO₃–x[SrTiO₃] composites ceramics, Appl. Phys. A: Mater. Sci. Process., 2012, 109, 715,  DOI:10.1007/s00339-012-7105-1.
33. S. Tripathy, K. Mishra, S. Sen and D. Pradhan, Dielectric and Raman Spectroscopic Studies of Na_0.5Bi_0.5TiO₃–BaSnO₃ Ferroelectric System, J. Am. Ceram. Soc., 2014, 97(6), 1846.
34. J. B. Babu, M. He, D. F. Zhang and J. Hao, Enhancement of ferroelectric properties of Na_1/2Bi_1/2TiO₃–BaTiO₃ single crystals by Ce dopings, Appl. Phys. Lett., 2007, 31, 102901,  DOI:10.1063/1.2709917.
35. C. S. Devi, G. S. Kumar and G. Prasad, Control of ferroelectric phase transition in nano particulate NBT–BT based ceramics, Mater. Sci. Eng., B, 2013, 178, 283,  DOI:10.1016/j.mseb.2012.12.001.
36. K. Datta, P. Thomas and K. Roleder, Anomalous phase transitions of lead-free piezoelectric xNa_0.5Bi_0.5TiO₃–(1 − x)BaTiO₃ solid solutions with enhanced phase transition temperatures, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 224105,  DOI:10.1103/PhysRevB.82.224105.
37. S. Bhandari, N. Sinha, G. Ray and B. Kumar, Flux growth of lead free (Na_0.5Bi_0.5)TiO₃–(K_0.5Bi_0.5)TiO₃ ferroelectric single crystals and their characterization, CrystEngComm, 2014, 16, 4459,  10.1039/c4ce00249k.

---