Combined experimental and computational insights into the key features of l-alanine l-alaninium picrate monohydrate: growth, structural, electronic and nonlinear optical properties†
Abstract
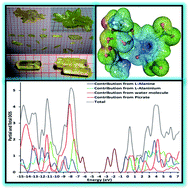
In the current work, we spotlight the novel key features of L-alanine L-alaninium picrate monohydrate (LALAPM) using a dual approach comprised of experimental and computational techniques. Single crystals of LALAPM have been grown indigenously in three different ratios (1 : 1, 1 : 5, 2 : 1) through a slow cooling technique. The formations of different types of crystals were recorded during the growth process and found to vary significantly from each other. The grown crystals were subjected to single crystal powder X-ray diffraction analysis to confirm their respective crystal structures. Additionally, ultraviolet-visible-near infrared, diffuse reflectance measurements and optical parameter analysis were performed. The state-of-art computational techniques were used to get the ground state molecular geometry of LALAPM at the B3LYP/6-31G* level of theory. Different important electro-optical parameters (complementary to the experimental results) including IR, Raman, and UV-visible spectra have been calculated at the same level of theory. The polarizability and first hyperpolarizability (both static and dynamic) were calculated to see the potential applications of LALAPM in nonlinear optics. Furthermore, several novel molecular level insights have been obtained in the form of the total and partial density of states, the HOMO–LUMO gap and electrostatic potential maps etc. The obtained quantum chemical findings were compared with experimental results. The static and frequency dependent dynamic first hyperpolarizability values of the LALAPM molecule are found to be 8.06 × 10−30 and 10.24 × 10−30 esu that are about 37 times and 59 times larger than those of the prototype urea molecule, respectively, at the same B3LYP/6-31G* level of theory. The obtained results indicate that the titled compound contains good nonlinear optical properties and can be treated as a good contender for optoelectronic device fabrications.

 Please wait while we load your content...
Please wait while we load your content...