Molecular growth of PAH-like systems induced by oxygen species: experimental and theoretical study of the reaction of naphthalene with HO (²Π_3/2), O (³P), and O₂ (³Σ⁻_g)

Abstract

To assess if reactions with oxygen species can induce a mass increase of polycyclic aromatic hydrocarbons, we exposed naphthalene molecules to an oxidative gas flow containing the radicals H and HO (²Π_3/2) and the diradicals O (³P) and O₂ (³Σ⁻_g). We observed the formation of 1- and 2-naphtol, 1,4-naphthoquinone, naphthalene-derived cyclic ethers, an ester from ring opening, and ether adducts containing two naphthalene units. We investigated the possible reaction pathways as a function of temperature by density functional calculations. We found that the reactivity is characterized by HO, O and H addition to naphthalene, or by H abstraction from it, with roles depending on temperature. In conclusion, oxygen species can promote, under the experimental conditions, mainly naphthalene oxidation and, to a lesser extent, substantial molecular growth, with an efficiency that the calculations indicate to depend on the system temperature. Future experiments should try to quantify key species to allow defining the relative importance of the various reaction mechanisms uncovered by ab initio calculations.

---

Introduction

Understanding the formation, growth, and possible oxidation of polycyclic aromatic hydrocarbons (PAHs, of which naphthalene is the lightest representative) is of interest in different fields, such as combustion,^1–6 environment⁷ and health, and even astrochemistry.^8–11 Chemical transformations of the hydrocarbon skeleton can see the intervention of small oxidants, among which are ground state O and O₂. Oxidation can accompany growth,^12–15 extending over the entire course of PAH and soot formation, but can also consume and destroy carbonaceous particles, depending on the combustion conditions, in particular at higher temperatures.^16–22 We feel that the role of oxidation processes in the growth of PAHs needs further clarification.^23–25

A practical way to study PAH oxidation and growth is by plasma techniques. For instance, treating benzene in an air plasma produces phenol, together with biphenyl (C₁₂H₁₀) and products with elemental formula C₆H₆O₂, C₁₂H₁₀O, and C₁₂H₁₀O₂.²⁶ The plasma conversion of naphthalene gives several byproducts, including benzaldehyde, acetophenone, benzoic acid, salicylic acid, phenylethyne, benzoic acid phenyl ester, and 1-hydroxycyclohexyl phenyl ketone (methanone).²⁷

To get some insights on the role of oxidative reactions in the growth of polycyclic aromatic hydrocarbons, we chose naphthalene as a model system, mainly because of its high vapor pressure.^5b Thus, we exposed naphthalene molecules to the outflow of a He/O₂ discharge and detected the reaction products. We observed both oxidation and molecular growth, the latter to a lesser extent. To rationalize the experimental results, we carried out DFT calculations to explore the possible reaction pathways to the observed products.²⁸ The focus of this investigation is “growth induced by oxygen species”. Therefore other interesting aspects, such as the formation of methyl substituent groups, are not examined in the present study.

Experimental method

To investigate the reactivity of oxygen species with naphthalene we have developed an experimental setup (sketched in Fig. 1) composed of an atmospheric pressure RF plasma jet to produce atomic oxygen,^29,30 an evaporator to produce gas-phase naphthalene, and a reactor where the reactants mix together.

Fig. 1 Scheme of experimental setup. RF PWS: RF power supply; M. BOX: matching box; HVP: high voltage probe; FC1, FC2, FC3, FC4: mass flow controllers; A: tungsten electrode; B: quartz tube; C: metallic reactor.

Naphthalene (99.9% purity) was melted in a bubbler at the temperature of 87 ± 1 °C, and transported into a heated pipe (115 °C) by a gentle flow of argon (500 sccm – FC3). The pipe contains a carrier flow of argon (1000 sccm – FC4) that transports naphthalene into the reactor C, where the pressure is around the atmospheric value. On the basis of our LIF measurements on OH in similar discharges and the known temperature of the reactor wall, we estimate the gas temperature to be about 400 K. Here the final concentration of naphthalene is estimated to be around 4 × 10¹⁶ molecules per cm³. In the reactor the naphthalene flow intercepts the discharge flow at different distances from the counter electrode (P1, 3 mm, and P2, 13 mm). The discharge feed gases, helium and oxygen, are controlled by two mass flow controllers (FC2, FC1). The total flow is set at 2000 sccm, the oxygen concentration can vary between 0 and 4.0%.

In nominal “pure” helium plasma, O₂ (less than 2 ppm) and humidity (less than 10 ppm) were still present in traces, and are responsible for the residual production of oxygen oxidants. In fact, in a similar set up we detected about 10¹² molecules per cm³ of HO by LIF measurements.

The discharge is sustained by a power supply (RF5S-RFPP) at 13.56 MHz via a matching box (AM5-RFPP), and occurs between the HV tungsten electrode (A, 1 mm of diameter, 170 mm of length) and the grounded mesh. To measure the power, voltage and current probes (Tektronix-P6015A and Magnelab CT-C1.0-BNC, respectively) were connected between the matching box and the tungsten electrode. V/I signals were recorded by a digital oscilloscope (WaveSurfer 104MXs-A, LeCroy, 1 GHz). The dissipated power was calculated by integrating the voltage times the current, by taking into account the time delay introduced by the probes. The actual power dissipated into the plasma was calculated as the difference between the power values measured with and without gas (discharge on and off, respectively).³¹ The plasma power turns out to depend on both the applied voltage and the gas composition. In particular by increasing the O₂ percentage, the plasma power decreases.

At the exit of the reactor, chemicals were condensed in a cold trap, T = −16 ± 1 °C. Uncondensed gases were collect in a canister and analyzed by FT-IR spectrometry (Bruker Equinox 55), with qualitative detection of CO₂ and CO in traces.

Condensed products were dissolved in 5 mL of acetonitrile and semi-quantitatively analyzed by chromatographic techniques, by using a Finningam Trace GC Ultra with both MS and FID detector. A DB-5 column (30 m length × 0.25 mm od × 0.25 µm width) was used. The flow rate of the carrier gas (He) in the capillary column was 1.5 mL min⁻¹. The column temperature was initially held at 60 °C for 1 minute, then ramped at 10 °C min⁻¹ up to 100 °C, at 4 °C min⁻¹ up to 190 °C and finally at 6 °C min⁻¹ up to 310 °C. The product structures were assigned by MS spectra, while the relative concentrations were quantified by the ratio of the area of the respective FID (Flame Ionized Detector) peaks with respect to the total area. Emission spectra were collected at position P1 (Fig. 1) by using a spectrograph Shamrock 303i (1200 lines per mm grating, 300 nm blaze), and an intensified CCD (Andor DH334T-18U-03). These spectra highlight the presence of O, OH, and H (see the ESI, Section 8†).

Theoretical method

Stable and transition structures (TS), corresponding to minima and first order saddle points on the energy hypersurface, were determined by Density Functional Theory (DFT),³² using the M06-2X functional³³ and gradient procedures.³⁴ The polarized split valence shell 6-311G(d,p)³⁵ was used in the DFT optimizations, and the nature of the critical points was checked by vibrational analysis. The energies were then refined by single-point energy computations with Dunning’s (polarized, valence-3ζ) cc-pVTZ basis set.³⁶ Hence the overall theory level is DFT(M06-2X)/cc-pVTZ//DFT(M06-2X)/6-311G(d,p). On the basis of previous studies^37,38 it is expected to perform acceptably. It also allows, in principle, the possible stacking of PAH-like parts of our growing systems, though stacking is expected to be of limited importance, due to the modest system size and flexibility.³⁹ Its performance in reactions involving radicals is also illustrated in the ESI, Section 1.†

For singlet diradicaloid structures, the wavefunction stability was checked, and obtained by relaxing it in the orbital rotations space. In any case, the desired spin densities, as expected for diradical structures, were obtained together with the wavefunction stability. The “automatic” closed shell singlet solution obviously yields, instead, zero spin densities. Since the resultant spin-mixing gives a better description of the electron distribution but alters the energy, the energy values were refined by Yamaguchi’s formula.⁴⁰

The 6-311G(d,p) thermochemical corrections gave estimates of the zero point vibrational energy (ZPE), by which the cc-pVTZ relative energies were corrected [ΔE_ZPE = Δ(E + ZPE)]. Also the relative Gibbs free energies (ΔG) were estimated (within the usual approximations)⁴¹ within a range of temperatures appropriate to encompass the sharply different conditions of the processes hinted at in the Introduction. Since the theoretical study focuses of course mainly on the experiment, ΔG values at T = 400 K are reported in the schemes. Given the experimental conditions, we can consider all species in thermal equilibrium with the surrounding gas. For this reason, we discuss in the text each ΔG^‡ barrier at 400 K with respect to the preceding minimum. When no TS on the E hypersurface is present, as in some radical couplings, and an all-downhill path to the intermediate product was found, the G surface was then probed, looking for a possible maximum. This was done by drawing G profiles along a path defined by series of constrained optimizations on the E surface, carried out at fixed values of a chosen distance R between the two moieties (see subsection B3). To define a G value, the vibrational frequency corresponding to the reaction coordinate was projected out.⁴² The rate constants were estimated by the Eyring equation within the Transition State Theory approximation, by exploiting the Thermo program of the MultiWell suite of programs.⁴³ Quantum mechanical calculations were carried out by using the GAUSSIAN09 system of programs.⁴⁴ Some kinetic tests were carried out by the numerical methods implemented in the program DYNAFIT.⁴⁵

Results and discussion

A. Experimental results

The concentration values reported below refer to compounds that condensed in the cold trap. The main naphthalene impurities (measured without plasma) are: methylnaphthalene isomers (C₁₁H₁₀), 410 ppm; dihydronaphthalene isomers C₁₀H₁₀ + tetrahydronaphthalene C₁₀H₁₂, 180 ppm; naphthol isomers C₁₀H₈O, 130 ppm. This is consistent with the assay (99.9%) of the used naphthalene.

Beside the unreacted naphthalene, the main detected compounds, after the interaction of naphthalene with the discharge flow at position P1, are:

(a) Initial O₂ = 0%, plasma power 14 W: dihydronaphthalene isomers C₁₀H₁₀ + tetrahydronaphthalene C₁₀H₁₂, 2700 ppm; naphthol isomers C₁₀H₈O, 1100 ppm; methylnaphthalene isomers C₁₁H₁₀, 280 ppm; binaphthalene isomers C₂₀H₁₄, 144 ppm.

(b) Initial O₂ = 0.5%, plasma power 11 W: naphthol isomers C₁₀H₈O, 6430 ppm; dihydronaphthalene isomers C₁₀H₁₀ + tetrahydronaphthalene C₁₀H_12, 730 ppm; naphthoquinone C₁₀H₆O₂, 670 ppm; dihydroepoxynaphthalene isomers C₁₀H₈O, 590 ppm; methylnaphthalene isomers C₁₁H₁₀, 360 ppm.

(c) Initial O₂ = 4%, plasma power 1.4 W: naphthol isomers C₁₀H₈O, 4330 ppm; dihydroepoxynaphthalene isomers C₁₀H₈O, 600 ppm; naphthoquinone C₁₀H₆O₂, 470 ppm; methylnaphthalene isomers C₁₁H₁₀, 560 ppm.

In addition we detected non quantifiable traces of C₂₀H₁₄O, C₁₀H₁₀O, C₁₀H₁₂O, hydroxybenzaldehyde C₇H₆O₂, 2-formylbenzaldehyde C₈H₆O₂, and C₂₀H₁₄O₂.

Experimental results indicate that reactions of naphthalene with reactive oxygen species, at least within our experimental conditions, generate mainly oxygenated products (of slightly higher molecular weight), and give only a small contribution to a more substantial molecular growth.

B. Reaction pathways

The focus of the theoretical modelling part of this study is on the possible routes to oxygenated products. Among them, we explored possible reaction pathways not only to the most important characterized products (naphthol, naphtho-1,4-quinone), but also to a minor but interesting product, which corresponds to a substantial mass increase. In fact, growth takes place via addition of a second naphthalene unit, and can consequently hint at the very early nucleation stages of oxidized carbon nanoparticles. Since the focus of our study is “growth induced by oxygen species”, the pathways for formation of tetrahydronaphthalene or formation of methyl substituent groups, though certainly interesting (and possible subject of further study), are not present in this section.

Scheme 1 (pathways which originate from the reactants, labeled 0, to 1-naphthol 2) and Scheme 2 (pathways to di-1-naphthylether 9) describe the evolution of a reacting system composed by one or two naphthalene molecules, plus O (³P), HO (²Π_3/2), O₂ (³Σ⁻_g), and H. The reactions involving these species are considered in different sequences. Then, Scheme 3 shows how naphtho-1,4-quinone can form. The reactants’ level, defined by the mentioned reactant species together, is the reference for the energetics reported in the schemes as ΔG at T = 400 K (the experimental temperature). A few exceptions regarding the reference for ΔG differences have been introduced for the sake of clarity, and explained in the legend of Scheme 2. Since an efficient thermalization can be safely assumed on the basis of the experimental conditions, we report instead in the text ΔG^‡ values with respect to each preceding minimum (barrier heights). Both the hydroxyl and ground state oxygen atom are considered as very reactive species, capable of triggering some reaction sequence towards oxygenated stable products. In the ESI, the purpose of Scheme S1† is to briefly comment on possible actions by ozone and the lowest singlet dioxygen state. Scheme S2† reports some side steps departing from Scheme 1.

Scheme 1 Formation pathways for 1-naphthol (C₁₀H₈O). ΔG values at DFT(M06-2X)/cc-pVTZ//DFT(M06-2X)/6-311G(d,p), taken with respect to the reactants level. Values originating from simple unimolecular homolytic H losses in green (taken as a reference); from bimolecular H abstractions operated by O₂ (³Σ⁻_g) in magenta, by O (³P) in blue, and by HO (²Π_3/2) in red.

Scheme 2 Reactions of 1 and 3 with naphthalene which could cause a mass increase. ΔG values at the DFT(M06-2X)/cc-pVTZ//DFT(M06-2X)/6-311G(d,p), taken with respect to the reactant level, unless otherwise indicated. Values originating from unimolecular homolytic H losses in green; from H abstraction operated by O (³P) in blue, by O₂ (³Σ⁻_g) in magenta, and by HO (²Π_3/2) in red. Radical couplings are emphasized by the purple color. Boxed values are taken with respect to 8, to avoid reporting too many figures, which inevitably originate from “mixed steps” 7–8 and 8–9. They allow a straightforward combination of values as desired.

Scheme 3 Possible pathway to 1,4-naphthoquinone. Boxed values make reference to 10.

B1. Pathways to 1-naphthol at T = 400 K. HO and O can give radical addition to the aromatic π system. They can in principle also abstract a hydrogen from naphthalene (see point b below). Position 1 is chosen here to study both steps.
a. O and HO additions to naphthalene. Scheme 1 shows that from the reactants (0), O atom π-addition to naphthalene entails overcoming a barrier of 10.2 kcal mol⁻¹ (all barriers discussed throughout the text are ΔG^‡ at 400 K with respect to the preceding minimum, but in the schemes the ΔG^‡ values are shown with respect to the reactants). By this addition, a first triplet adduct is obtained (1), which lies 12.7 kcal mol⁻¹ below the reactants’ reference level. This C₁₀H₈O species can undergo isomerization via 1,2 H shift to triplet naphthol (³2). Though ³2 is located at −29.2 kcal mol⁻¹, the relevant barrier (ΔG^‡ = 26.1 kcal mol⁻¹) is quite high. Therefore, this first pathway does not seem to be promising for naphthol formation. An alternative step is H loss from 1, to give the 1-naphthoxyl radical 3. When dealing with H losses, we report in Scheme 1 the energetics for the unimolecular homolytic H loss as green ΔG data. These provide a reference for H abstraction steps conducted instead by: O₂ (³Σ⁻_g), magenta figures; O (³P), blue figures; or HO (²Π_3/2), red figures (but possibly acquire also some importance in themselves at the highest T values). For the 1–3 step, the data for O-mediated H abstraction are not present in Scheme 1, because O operates in this case differently: it adds to the oxyl oxygen and gives a peroxyl diradical (as discussed in the ESI, Section 4†). The most favorable pathway to obtain the intermediate 3 (irreversibly) is via H abstraction by HO, by overcoming a barrier of 6.3 kcal mol⁻¹. The intermediate 3 is a resonant species, with spin densities mainly on oxygen and on the two “allylic” positions of the substituted ring (compare sketch). The spin density distribution obtained for 3 should actually favor those radical spin couplings with a H atom that involve its 2 and 4 positions.⁴⁶ A significant uncertainty about the assignment of the peak either to naphthol 2 or to its isomeric ketones prevents experimental assessment of which channel (between those going through 3) is more important. On the other hand, the relevant computed barriers for the steps departing from 3 are almost identical.

The HO radical addition to the π system of naphthalene (bottom of Scheme 1) presents a barrier close to that of the O atom addition (ΔG^‡ = 10.3 kcal mol⁻¹), and also the radical 4 so obtained is located close to 1, at 12.4 kcal mol⁻¹ below the reactants. So, 1 and 4 are expected to form with the same intrinsic rate and irreversibly. A theoretical estimate of their relative amounts would depend in the end upon hypothesized initial densities of O and HO. As before, different H loss modes can take place, of which H abstraction by O this time takes place (compare step 1–3). Moreover, it is the easiest, since it presents a barrier of only 0.4 kcal mol⁻¹. HO comes next and requires overcoming a barrier of 4.5 kcal mol⁻¹. The final product, singlet 1-naphthol 2, is again unavoidably associated with a multiplicity of ΔG values, depending on the nature of the preceding H loss.

Among the π-addition promoted pathways to ¹2, that by HO, followed by H abstraction by the O atom in 4, which presents a very small barrier, would seem the most promising, on the basis of the free energy barriers only. On the same basis, however, 1 and 4 are formed as easily, and the two relevant backwards steps are not easy. Therefore, the computed kinetic constants describe 4–2 as a potentially more prompt naphthol production channel, while 1–3–2 is expected to proceed more slowly – though inexorably – towards 3, and then, with a barrier of 7.3 kcal mol⁻¹, irreversibly to the products. Therefore, a first point is that the relative intrinsic importance of the two pathways will be time-dependent. A second important point is that their ability to produce naphthol will in the end depend on the concentrations of O and HO. Since an estimate of HO density is available from our measurements, while a large uncertainty on O atom density subsists in our study, we have carried out kinetic simulations,⁴⁴ within this simple scheme, hypothesizing three increasing O concentrations: 10¹², 10¹⁴, and 10¹⁶ atoms per cm³ (the last one is that reported in ref. 29 and 30). Following this density sequence, the amount of naphthol produced via pathway 1–3–2 varies from 35 to 65 and again 65% (where step 1–3 proceeds via H abstraction by O₂, due to its higher concentration with respect to OH), and from 18 to 34 and 35% (step 1–3: sheer H loss). Naphthol obtained through 4 has a role only at the lowest O density, since it drops from 47 to 1 and then to 0% (step 4–2: H abstraction by O). More details are available in the ESI, Section 6.†

Coming back to the initial O atom adduct, a possible intersystem crossing (ISC) in ³1 → “¹1” would give a barrierless ring closure to the corresponding (closed shell) epoxide isomer. An epoxide product, and also another ether, a benzo-substituted 7-oxabicyclo[2.2.1]heptadiene, are in fact detected (see points b and c of Subsection A).

b. Role of H abstraction from naphthalene. On the other hand, H abstraction from naphthalene (position 1 of naphthalene is involved), if occurring, would imply the existence of an expectedly easy way to singlet 1-naphthol ¹2, via spin coupling between the hydroxyl and naphthyl radicals. (Naphthyl radical 5 will be further discussed below by making reference to Scheme 2, because it will be needed to interpret the formation of a minor product containing two naphthalene units.) The possible H abstraction from naphthalene operated by O or HO to give 5 has barriers at T = 400 K of 16.9 and 12.8 kcal mol⁻¹, respectively. Thus, addition at 400 K presents lower barriers than H abstraction, though this difference is only 2.5 kcal mol⁻¹ in the case of HO intervention. These barriers translate to a kinetic datum, the branching ratio, for each species and for the two reaction types. The branching ratios are defined, for each process conducted by each reactive species X (O₂, O, HO), as where k_X is either the H loss rate constant from naphthalene, or an “effective” addition rate constant (k_add,eff) to naphthalene, for each X (the summation runs on all X_i’s). The latter is defined by taking into account the two rate constants relevant to the addition step, k₁ and k₋₁; then the role of the latter is lessened by taking into account some possible exit channels from the adduct. See the ESI, Section 2,† for further details on the definition of the “effective” addition rate constant k_add,eff, and its behavior against the experimental data of Lorenz and Zellner for the reaction of hydroxyl and naphthalene.⁴⁷ Since we forcedly take into account only some of the exit channels, this lessening provides only an upper limit of the influence of k₋₁, which could actually be smaller if other exit channels were taken into account. From another point of view, it provides a lower limit for the rate at which the reactant naphthalene disappears. In ∑k_X, the summation runs over three “effective” additions and three H abstractions operated by X (see also the next subsection for more details). The most prominent values at T = 400 K are, for the additions sketched in Scheme 1, α_O = 0.80 and α_HO = 0.18. The next values appear as minor contributions, which add up approximately to 2% of the total at the experimental temperature, and H-abstraction by HO does not seem capable of competing efficiently with the additions of the O atom or HO itself. In Scheme 1, to describe the most probable pathways towards 1-naphthol, contributing to the major isomer products, we have accordingly reported only the data for the most probable contributions.

The naphthyl radical 5 can form in principle in different ways: H abstraction by O₂, O, HO, and H.⁴⁸ We find that their relative importance can vary drastically with temperature, and this aspect will be discussed in subsection B2. But another possibility for naphthyl formation could come from the exposure of naphthalene to UV radiation from de-excitation of the present excited species, such as HO, N₂, O, or He. We are however inclined to rule out this channel since their emission spectra have been recorded in the range 240–1000 nm, and the most energetic radiation available is one HO band at 280 nm. Since the threshold value for C–H homolysis is estimated to be 258 nm (from its D_e = 111 kcal mol⁻¹) we deem that discarding the contribution of a photolytic pathway is safe. A further point is that the presence of dioxygen is observed to quench these emission bands significantly.

B2. H-abstraction vs. addition: T dependence. In the preceding subsection, when comparing the experimental results with the computational G barrier estimates at T = 400 K, H abstraction from naphthalene has been put aside as a potential minor contribution for naphthol formation. However, given the variety of situations envisaged in the Introduction, computational results for a range of temperatures up to 1300 K are also presented. In fact, an interesting point is inspecting if and how addition to the π-system of naphthalene can compete with hydrogen abstraction from it, when T is raised to combustion temperatures.

Fig. 2 illustrates how the rate constants k_add,eff (“effective”, for addition; continuous lines) and k_abs (H-abstraction from position 1; dashed lines) change with T. Two comparisons can be drawn. The first one is for each single species, HO or O (lines of the same color), comparing addition with H-abstraction. The second one between different species: the slopes of their lines will put their competition at each T on a ground that varies with T.

Fig. 2 Rate constants k_X as a function of T. Red lines: X = HO; blue lines: X = O. k_X “effective” (see text) for X addition to naphthalene (continuous lines) vs. H-abstraction from its position 1 (broken lines). For both species, addition is easier at lower temperatures; then, a crossing occurs for HO just around 850 K, and a similar crossing for O at ca. 1600 K (not represented here, see the ESI file, Section 5†).

For X = HO (red lines) not only the slopes but also the behavior of the k_add,eff and k_abs lines are different. A crossing is present at ca. 850 K. For the oxygen atom, the two blue lines start, at low T, more far apart; then they hint at a crossing at a higher T than HO, to be encountered at ca. 1600 K, as shown in the ESI, Section 5.† There, a more detailed comment on the changing slope of the HO addition line compared with the monotonic slope of its H abstraction counterpart can also be found.

Therefore, when both HO and O are present, addition dominates in the whole range 300–1300 K. It will be operated faster by HO up to ca. 750 K, then, beyond that temperature, the oxygen atom will add faster. On the other hand, H-abstractions by O and HO will tend to become as easy as HO addition around 850 K, where it declines, but are still slower than O addition at the highest T values reported in Fig. 2. Only at higher T values than represented (beyond 1600 K, approximately), the individual H abstractions will become faster.⁴⁹ HO is more inclined towards H abstraction than the oxygen atom up to ca. 1250 K, beyond that temperature the reverse is true.

A further piece of information is provided by the branching ratios 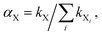(X = HO, O), whose values have already been briefly discussed in connection with the experimental temperature, 400 K. Since their variations with T reflect the behavior of a single kinetic constant k_X with respect to the sum of all five constants considered,⁵⁰ their growth and decline are very diverse, as can be seen in Fig. 3. These are the data which, in conjunction with hopefully sensible guesses for the concentrations of the species discussed, at the various T values, might help us to interpret the outcome of the experiment in terms of product yields. Some density values are available in the literature for specific experiments, and extending over some temperature ranges.^17,21

Fig. 3 Branching ratios, defined for each reactive species X (X = HO, O) as (see main text). Addition to naphthalene: continuous lines. H-abstraction from its position 1: broken lines. Red lines: X = HO. Blue lines: X = O. Black continuous line: sum of the two additions. Black dashed line: sum of the two H abstractions. At the lowest temperatures HO addition dominates, while O addition prevails beyond 800 K. Beyond 1300 K, H abstractions prevails.

Generally, we see in Fig. 3 that, at lower T values, additions (expressed as ∑α_X, black continuous line) prevail, but decline constantly as T increases. By contrast, the ∑α_X for H abstractions (black dashed line) gradually becomes more important as T rises, with a crossing just beyond 1300 K (at lower T than suggested by the individual rate constants). Addition lines present conspicuous changes upon T variation. By contrast, H abstractions exhibit more moderate and monotonic changes, though slope variations are evident. Inspecting each line in more detail, α_HO (addition) prevails completely at the lowest temperatures, but declines continuously in a steep way up to 900 K. By contrast, α_O (addition) rises abruptly from 300 K up to 900 K. Around 750 K it passes α_HO. Then, after a maximum at ca. 900 K, α_O keeps prevailing among additions up to ca. 1000 K, but it exhibits a regularly declining behavior.

The importance of H-abstraction from naphthalene (dashed lines) rises with T in a steeper way for the O atom (blue). These trends indicate qualitatively that the preferred pathways and the final outcome will depend significantly on temperature.

B3. Mass increase pathways. Other bimolecular transformations of 1 or 3 involving again naphthalene might bring about an interesting growth of the initial reacting system through formation of oxygen-containing adducts (Scheme 2).

It must be stressed that higher-mass products are detected at 400 K only in low concentrations. Radical addition of 1 to another naphthalene by engaging one of its “allylic” carbon (here explored only for position 4) is not promising since ΔG^‡ = 31.9 kcal mol⁻¹. It would produce the adduct 6 (C₂₀H₁₆O). A better situation is encountered if the attack onto naphthalene is conducted by the oxyl terminal of 1: it entails a barrier of 20.3 kcal mol⁻¹, to give the adduct 7, located 10.4 kcal mol⁻¹ below the reactants. Though the barrier is below the previous one, its height is not negligible. If 7 could be attained, then different H losses, from the position geminal to the oxyl oxygen, could follow to get 8 (C₂₀H₁₅O). The simple loss by homolytic bond cleavage, from which two fragments positioned 5.7 kcal mol⁻¹ above the reactants are obtained, requires overcoming a high barrier (ΔG^‡ = 31.8 kcal mol⁻¹) and is discarded again. If this step is instead mediated by O₂, the abstraction barrier is only 11.1 kcal mol⁻¹ above 7. For the O₂-mediated pathway, the products, 8 + HOO˙, are placed 32.9 kcal mol⁻¹ below the reactants. For the HO-mediated abstraction, the barrier is lower, 8.9 kcal mol⁻¹ high with respect to 7, and the attained well is even deeper: −100.6 kcal mol⁻¹, for 8 + H₂O. When the oxygen atom operates the H_gem abstraction from 7, the resulting well is 86.7 kcal mol⁻¹ deep, in correspondence of 8 + HO˙. The step is apparently barrierless on the E hypersurface, but a G profile has not been defined because an alternative pathway, similarly ending to 8 formation, departs from 1 in a way significantly easier than the step 1–7. Therefore, it is not worthwhile to insist in the laborious task of defining the G barrier for the O-mediated step 7–8.

From 1, the 1-naphthoxyl radical intermediate 3 forms via H loss. H loss can occur again by following steps of different nature (as already seen), with the exception of H abstraction by O (Scheme 3 illustrates the reaction of O with 3). Then 3 can add to a naphthalene molecule and form 8. The 3–8 addition step entails however a large barrier, because the intermediate 3 lies in more or less deep G wells: −20.5, −59.1, or −126.8 kcal mol⁻¹, respectively (HOO˙ or HO˙ or H₂O free energies taken into account). This trait makes the barrier for the step 3–8 36.3 kcal mol⁻¹ high, obviously in all three cases. The energetics reported for the intermediate 8 is the same, either if defined for the steps 1–7–8, or from 1–3–8, since in all cases the chemical events are the same, though taking place in a different order. In conclusion, since thermalization is assumed, both pathways examined so far, 1–7–8 and 1–3–8, do not seem promising.

However, the intermediate 8 could also be obtained from the radical addition of 1 with the naphthyl radical 5 (see end of Section B1 and note 50). In 1, the spin density on C4 is 0.65 (0.56 on C2), while in 5 the unpaired electron is localized (spin density 1.03). This simple radical coupling does not present a barrier on the energy surface. Therefore, a maximum was defined along a free energy profile, by choosing, as intermoiety distance R, the C4(1)–C1(5) distance. The G maximum occurs early, in a geometrical sense, at R = 3.5 Å. The corresponding barrier is 11.5 kcal mol⁻¹ high.

From 8, however formed, and if formed, a further and final H loss would lead to 9 (C₂₀H₁₄O), which is detected experimentally in small amounts. Boxed free energy difference values are taken in this case with respect to 8, departing from the choice of making mostly reference, in the schemes, to the reactants’ level. This is to avoid reporting a plethora of values, which unavoidably originate from the possibility of having “mixed” steps 7–8 and 8–9 (for instance, if O₂ operates first, then HO), plus from the radical coupling step. The boxed values allow a straightforward combination of values, as desired. The relevant ΔG^‡ barriers are: 29.8 kcal mol⁻¹ for pure homolysis, but only 15.4 if the H abstraction is O₂-mediated, 12.4 if O-mediated, and even 2.1 kcal mol⁻¹ below 8 if the abstraction is HO-mediated, due to the presence of a complex which precedes the TS.

Still another possibility is offered by the spin coupling between the radical 3 and naphthyl 5. It stems from 3, which forms in the easiest way, compared to 1–7 and 1–8. Then the 3 + 5 addition requires overcoming a barrier of 9.6 kcal mol⁻¹. As seen before, the spin density on position 4 of 3 is 0.51, thus lower than the corresponding value in 1, 0.65. This difference could explain why this radical coupling presents a barrier. To qualify these last channels, 1–8 and 1–3–8, as more promising, we need first to pose the question of how much naphthyl 5 will be actually present. From the 1,1-binaphtyl detected, one could surmise that the naphthyl radical is present also at low temperatures, as that of the experiment.

B4. A possible pathway to 1,4-naphthoquinone. Following initial O addition to naphthalene, a second barrierless O atom addition to intermediate 3 can take place. The intermediate 10 thus generated is taken as a reference for the boxed free energy difference values of Scheme 3. When 10 undergoes H loss, 11 (1,4-naphthoquinone) is produced either by sheer homolysis (more demanding), or via H abstractions. The blue value (H abstraction conducted by an O atom) is again missing, as in Scheme 1 for the step 1–3. It is not reported because, in 10, the incoming O atom prefers again to add to the oxyl radical oxygen, rather than abstract its gem hydrogen.

B5. Products not containing oxygen. Products which do not incorporate oxygen have been detected. Since they can be thought of as forming also upon the action of oxygen species (such as dihydro- and tetrahydro-naphthalene, binaphthyl), we have explored to some extent this possibility. For instance, an H transfer from the initial adducts 1 or 4 to naphthalene (0) could explain the formation of dihydro- and tetrahydronaphthalene. To investigate this possibility we have studied the reaction steps shown in Scheme 4. The intermediate 12 can be seen as a relatively direct precursor of dihydronaphthalene, via further H addition (which can take place subsequently in more than one way). While the former addition seems feasible, the latter requires overcoming a rather large barrier.

Scheme 4 Possible formation pathway for a direct precursor of 1,1′-dinaphthyl. ΔG values at the DFT(M06-2X)/cc-pVTZ//DFT(M06-2X)/6-311G(d,p) computational level.

On the other hand, the formation of the naphthyl radical 5 (possibly formed via H abstraction from 0 operated by an oxygen species)⁵⁰ could open the way, upon addition to naphthalene (with a barrier of almost 18 kcal mol⁻¹), to the formation of binaphthyl (Scheme 5). Here, free energy differences are taken with respect to 0 + 5, in order to avoid an excess of values, and so deviating from the more general choice, made in the schemes, of making reference to the reactants level.

Scheme 5 Possible pathway to 1,1′-binaphthyl. The free energy level of naphthalene + naphthyl radical (which can form in several ways) has been set arbitrarily to zero (see end of Section B1 and note 50).

Dihydronaphthalene and binaphthyl share a common trait. We recall that, when [O₂ ] = 0%, dihydronaphthalene isomers plus tetrahydronaphthalene were detected at a concentration of 2700 ppm; binaphthyl isomers at 144 ppm. When [O₂ ] = 0.5%, the collective hydrogenated product concentration dropped to 730 ppm, to disappear altogether when [O₂] = 4%. Binaphthyl is conversely already absent at [O₂ ] = 0.5%. These results suggest that the formation of the three products is better achieved through reaction pathways not involving oxygen species. When oxygen species are present the fate of radical species as 5 could be different (a possible alternative involvement of the naphthyl radical was shown in Scheme 2).

Conclusions

The reactions of naphthalene with oxygen species (O, OH, O₂) at 400 K produce mainly 1- and 2-naphtol, followed by 1,4-naphthoquinone, whose yield is one order of magnitude lower. Interestingly, also ether adducts with two naphthalene units form in smaller amounts. Thus oxidation reactions can promote the molecular growth of PAHs, in addition to producing oxygenated products.

Density functional calculations carried out to clarify the formation mechanisms outline the critical role of HO, O and H additions to naphthalene, and H abstractions from it. At the experiment temperature (T = 400 K) addition reactions to naphthalene prevail, and explain the formation of naphthol. The dependence on temperature of these additions and of H abstraction processes suggests however that, upon temperature increase, the addition-initiated mechanism, described as dominant in the experiment, could be flanked by an abstraction-initiated one. Regarding the possible system growth by addition of a second naphthalene molecule, the most viable mechanism found relies on the presence of the naphthyl radical, and could consequently depend significantly on temperature. This suggests in turn a reason why at T = 400 K its yield is quite low: the H abstraction from naphthalene is difficult. It is legitimate to surmise that, at a higher T, its yield might be larger.

Our results suggest that different oxidation/growth mechanisms prevail at different temperatures. Thus there is no single pattern for PAH growth, which depends instead on the specific environment.

Acknowledgements

We thank one referee for constructive criticism. We acknowledge financial support from Provincia Autonoma di Trento and CNR-IMCB by the ENAM project. We also thank the staff of Laboratori Didattici, Department of Physics UNITN, who made available their instrumentation.

References and notes

1. A. D’Anna, Proc. Combust. Inst., 2009, 32, 593–613.
2. U. Pöschl, T. Letzel, C. Schauer and R. Niessner, J. Phys. Chem. A, 2001, 105, 4029–4041.
3. R. M. Kamens, J. Guo, Z. Guo and S. R. McDow, Atmos. Environ., Part A, 1990, 24, 1161–1173.
4. K.-H. Homann, Angew. Chem., Int. Ed., 1998, 37, 2434–2451.
5. (a) B. J. Finlayson-Pitts and J. N. Pitts Jr, Chemistry of the Upper and Lower Atmosphere, Academic Press, New York, 2000, ch. 10; (b) See, in particular, Table 10.6.
6. See for instance: H. Böhm and H. Jander, Phys. Chem. Chem. Phys., 1999, 1, 3775–3781; E. B. Ledesma, M. A. Kalish, P. F. Nelson, M. J. Wornat and J. C. Mackie, Fuel, 2000, 79, 1801–1814; I. Naydenova, P. A. Vlasov and J. Warnatz, Proc. Eur. Comb. Meeting, 2005; C. Jäger, F. Huisken, H. Mutschke, I. Llamas-Jansa and T. Henning, Astrophys. J., 2009, 696, 706–712; C. Jäger, H. Mutschke, F. Huisken, S. Krasnokutski, A. Staicu, Th. Henning, W. Poppitz and I. Voicu, Astrophys. J., Suppl. Ser., 2006, 166, 557–566.
7. L. A. Sgro, A. Simonelli, l. Pascarella, P. Minutolo, D. Guarnieri, N. Sannolo, P. Netti and A. D’Anna, Environ. Sci. Technol., 2009, 43, 2608–2613.
8. Two recent reviews: A. G. G. M. Tielens, Rev. Mod. Phys., 2013, 85, 1021–1081; M. Agúndez and V. Wakelam, Chem. Rev., 2013, 113, 8710–8737.
9. S. E. Malek, J. Cami and J. Bernard-Salas, Astrophys. J., 2012, 744, 16–24; C. Boersma, C. W. Bauschlicher Jr, A. Ricca, A. L. Mattioda, E. Peeters, A. G. G. M. Tielens and L. J. Allamandola, Astrophys. J., 2011, 729, 64–78; J. M. Bakker, B. Redlich, A. F. G. van der Meer and J. Oomens, Astrophys. J., 2011, 741, 74–83; A. G. G. M. Tielens, Annu. Rev. Astron. Astrophys., 2008, 46, 289–337; P. M. Woods and K. Willacy, Astrophys. J., 2007, 655, L49–L52; E. F. van Dishoeck, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 12249–12256; E. H. Wilson and S. K. Atreya, Planet. Space Sci., 2003, 51, 1017–1033; I. Cherchneff, J. R. Barker and A. G. G. M. Tielens, Astrophys. J., 1991, 377, 541–552; L. J. Allamandola, A. G. G. M. Tielens and J. R. Barker, Astrophys. J., Suppl. Ser., 1989, 71, 733–775.
10. A. Occhiogrosso, S. Viti and N. Balucani, Mon. Not. R. Astron. Soc., 2013, 432, 3423–3430.
11. P. F. Goldsmith, R. Liseau, T. A. Bell, J. H. Black, J.-H. Chen, D. Hollenbach, M. J. Kaufman, D. Li, D. C. Lis, G. Melnick, D. Neufeld, L. Pagani, R. Snell, A. O. Benz, E. Bergin, S. Bruderer, P. Caselli, E. Caux, P. Encrenaz, E. Falgarone, M. Gerin, J. R. Goicoechea, Å. Hjalmarson, B. Larsson, J. Le Bourlot, F. Le Petit, M. De Luca, Z. Nagy, E. Roueff, A. Sandqvist, F. van der Tak, E. F. van Dishoeck, C. Vastel, S. Viti and U. Yıldız, Astrophys. J., 2011, 737, 96–113; U. A. Yıldız, K. Acharyya, P. F. Goldsmith, E. F. van Dishoeck, G. Melnick, R. Snell, R. Liseau, J.-H. Chen, L. Pagani, E. Bergin, P. Caselli, E. Herbst, L. E. Kristensen, R. Visser, D. C. Lis and M. Gerin, Astron. Astrophys., 2013, 558, A58.
12. J. F. Griffiths and J. A. Barnard, Flame and Combustion, Blackie Academic and Professional, 1995, § 6.8; in particular: pp. 117 and 118. The crossings in Fig. 6.7 are related to the bell-shaped soot yield curves, as a function of T, which are observed oftentimes (see ref. 20 ch. 18, in particular pp. 294 and 295).
13. H. S. Homan, Combust. Sci. Technol., 1983, 33, 1–15.
14. N. E. Sánchez, A. Callejas, Á. Millera, R. Bilbao and M. U. Alzueta, Energy Fuels, 2013, 27, 7081–7088.
15. J. Xi and B.-J. Zhong, Chem. Eng. Technol., 2006, 29, 665–763.
16. B. R. Stanmore, J. F. Brilhac and P. Gilot, Carbon, 2001, 39, 2247–2268.
17. F. Xu, A. M. El-Leathy, C. H. Kim and G. M. Faeth, Combust. Flame, 2003, 132, 43–57.
18. On soot gasification by O₃ and NO₂: S. Kamm, H. Saathoff, K.-H. Naumann, O. Möhler and U. Schurath, Combust. Flame, 2004, 138, 353–361.
19. Two DFT studies modeling gasification: A. Montoya, F. Mondragòn and T. N. Truong, Fuel Process. Technol., 2002, 77–78, 125–130; J. F. Espinal, A. Montoya, F. Mondragòn and T. N. Truong, J. Phys. Chem. B, 2004, 108, 1003–1008.
20. J. Warnatz, U. Maas and R. W. Dibble, Combustion, Springer, Verlag, 4th edn, 2006, ch. 18, pp. 282–296.
21. C. H. Kim, F. Xu and G. M. Faeth, Combust. Flame, 2008, 152, 301–316.
22. I. Glassman and R. A. Yetter, Combustion, Elsevier, 4th edn, 2008, ch. 8.E, in particular §3.
23. S. Thomas, E. B. Ledesma and M. J. Wornat, Fuel, 2007, 86, 2581–2595.
24. S. Thomas and M. J. Wornat, Fuel, 2008, 87, 768–781.
25. A. Fuentes, R. Henríquez, F. Nmira, F. Liu and J.-L. Consalvi, Combust. Flame, 2013, 160, 786–795.
26. D. Ascenzi, P. Franceschi, G. Guella and P. Tosi, J. Phys. Chem. A, 2006, 110, 7841–7847.
27. A. A. Abdelaziz, T. Seto, M. Abdel-Salam and Y. Otani, J. Hazard. Mater., 2013, 246, 26–33.
28. The similar “benzene plus O atom” reacting system has been the subject of theoretical (a–c), or joint experimental/theoretical (d), studies appeared in recent years (a) J. F. Orrego, T. N. Truong and F. Mondragòn, J. Phys. Chem. A, 2008, 112, 8205–8207; (b) T. L. Nguyen, J. Peeters and L. Vereecken, J. Phys. Chem. A, 2007, 111, 3836–3849; (c) G. Vourliotakis, G. Skevis and M. A. Founti, Energy Fuels, 2011, 25, 1950–1963; (d) C. A. Taatjes, D. L. Osborn, T. M. Selby, G. Meloni, A. J. Trevitt, E. Epifanovsky, A. Krylov, B. Sirjean, E. Dames and H. Wang, J. Phys. Chem. A, 2010, 114, 3355–3370; (e) S. J. Sibener, R. J. Buss, P. Casavecchia, T. Hirooka and Y. T. Lee, J. Chem. Phys., 1980, 72, 4341–4349; (f) H.-F. Chen, C.-W. Liang, J. J. Lin, Y.-P. Lee, J. F. Ogilvie, Z. F. Xu and M. C. Lin, J. Chem. Phys., 2008, 129, 174303.
29. J. Y. Jeong, J. Park, I. Henins, S. E. Babayan, V. J. Tu, G. S. Selwyn, G. Ding and R. F. Hicks, J. Phys. Chem. A, 2000, 104, 8027–8032.
30. S. Reuter, K. Niemi, V. Schulz-von der Gathen and H. F. Döbele, Plasma Sources Sci. Technol., 2009, 18, 015006.
31. S. Hofmann, A. F. H. van Gessel, T. Verreycken and P. Bruggeman, Plasma Sources Sci. Technol., 2011, 20, 065010.
32. R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989, ch. 3.
33. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
34. J. A. Pople, P. M. W. Gill and B. G. Johnson, Chem. Phys. Lett., 1992, 199, 557–560; H. B. Schlegel, Computational Theoretical Organic Chemistry, ed. I. G. Csizsmadia and R. Daudel, Reidel Publishing Co., Dordrecht, The Netherlands, 1981, pp. 129–159; H. B. Schlegel, J. Chem. Phys., 1982, 77, 3676–3681; H. B. Schlegel, J. S. Binkley and J. A. Pople, J. Chem. Phys., 1984, 80, 1976–1981; H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218.
35. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654.
36. R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
37. D. Trogolo, A. Maranzana, G. Ghigo and G. Tonachini, J. Phys. Chem. A, 2014, 118, 427–440.
38. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
39. A. Maranzana, A. Indarto, A. Giordana, G. Tonachini, V. Barone, M. Causà and M. Pavone, J. Chem. Phys., 2013, 139, 244306.
40. S. Yamanaka, T. Kawakami, K. Nagao and K. Yamaguchi, Chem. Phys. Lett., 1994, 231, 25–33; K. Yamaguchi, F. Jensen, A. Dorigo and K. N. Houk, Chem. Phys. Lett., 1988, 149, 537–542 See also: J. Baker, A. Scheiner and J. Andzelm, Chem. Phys. Lett., 1993, 216, 380–388 For discussions concerning the effect of spin projection on the performances of DFT methods, see: J. M. Wittbrodt and H. B. Schlegel, J. Chem. Phys., 1996, 105, 6574–6577; E. Goldstein, B. Beno and K. N. Houk, J. Am. Chem. Soc., 1996, 118, 6036–6043.
41. See for instance: W. J. Hehre, L. Radom, P. v. R. Schleyer and J. A. Pople, Ab Initio Molecular Orbital Theory, J. Wiley & Sons, 1985, ch. 6.3. And, from the Gaussian site: http://www.gaussian.com/g_whitepap/vib.htm (on how vibrational frequencies are computed) and http://www.gaussian.com/g_whitepap/thermo.htm (on the computation of partition functions and Gibbs free energy).
42. A. G. Baboul and H. B. Schlegel, J. Chem. Phys., 1997, 107, 9413–9417.
43. MultiWell-2012.2 Software, July 2012, designed and maintained by J. R. Barker with contributors N. F. Ortiz, J. M. Preses, L. L. Lohr, A. Maranzana, P. J. Stimac, T. L. Nguyen and T. J. Dhilip Kumar, University of Michigan, Ann Arbor, MI, http://aoss.engin.umich.edu/multiwell/.
44. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009.
45. P. Kuzmič, Anal. Biochem., 1996, 237, 260–273 http://www.biokin.com/dynafit/index.html See also: P. Kuzmič, DynaFit, Version 4.0, May 2014.
46. A side result is that the H addition to position 4 is described computationally as giving a ketone which is located 9.7 kcal mol⁻¹ higher in energy than ¹2.
47. (a) R. Atkinson, J. Phys. Chem. Ref. Data, Monogr., 1989, 1; in particular, for naphthalene, see page 237. (b) K. Lorenz and L. Zellner, Ber. Bunsenges. Phys. Chem., 1983, 87, 629–636.
48. H abstraction barriers (at T = 400 K): ΔG^‡ = 66.6 (O₂); 12.8 (HO); O: 16.9 (O); 22.3 (H) kcal mol⁻¹.
49. This is a behavior experimentally known also for other systems, as in the reaction of HO with alkylated benzenes. For toluene and 1,2,3-trimethylbenzene, an Arrhenius plot presents two distinct regions, with opposite slope, pertaining to addition and H-abstraction, and a transition zone, a discontinuity, located roughly around 340 K. See: R. A. Perry, R. Atkinson and J. N. Pitts Jr, J. Phys. Chem., 1977, 81, 296–303 See also ref. 47a, in particular pages 204–241. However, in our case, and for every abstracting species X, H-abstraction occurs at a higher temperature than in the alkylated benzenes case. This feature originates from the fact that aromatic hydrogens are much less inclined toward homolytic cleavage than those of alkyl groups bound to an aromatic ring. This trait is illustrated for instance by D₀ values: e.g. 111 kcal mol⁻¹ to get the phenyl radical Ph˙ from benzene, vs. only 88 to get the resonance stabilized benzyl, PhCH₂˙ from toluene. See: M. B. Smith and J. March, March’s Advanced Organic Chemistry, Wiley-Interscience, 6th edn, 2007, ch. 5, Table 5.4; R. H. Chen, S. A. Kafafi and S. E. Stein, J. Am. Chem. Soc., 1989, 111, 1418–1423.
50. H abstractions by HO, O, and H are taken into account. Concerning addition, only for HO and O addition are instead considered, because H addition to naphthalene, followed by H abstraction (from the saturated carbon) gives again naphthalene.

---

Footnote

† Electronic supplementary information (ESI) available: Validation of the computational level, schemes with possible roles of O (¹Δ_g), O₃, hydroperoxide, comparison with experimental data, kinetic simulations, table of energies, and optimized geometries. See DOI: 10.1039/c5ra05129k

---