“Armed and disarmed” theory in the addition of an azide radical to glucals

Abstract

In this report, “armed and disarmed” theory was used to explain the selectivity of azide radical addition to glucals. We discovered that “armed” glucals were prone to undergo a kinetic process. The torsional strains govern the selectivity. Meanwhile, “disarmed” glucals preferred thermodynamic radical addition. We also applied our method to synthesize a sialic acid containing trisaccharide.

---

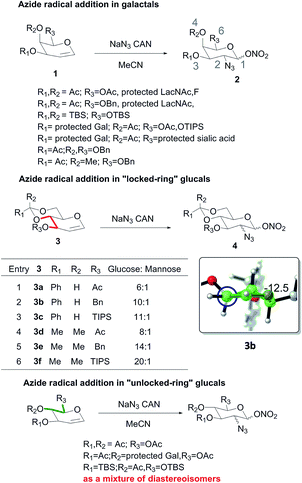
An azide radical is a powerful tool in organic chemistry to introduce C–N bonds. The addition of an azide radical to 1,5-anhydro-2-deoxy-hex-1-enitols called “glycal” conveniently converts them into hexosamines, which have widespread applications in carbohydrate chemistry. Previous reports are summarized in Scheme 1. Galactal derivatives 1 were diastereoselectively converted to the corresponding 2-deoxy-2-azide galactoses 2.¹ Similarly, 2-deoxy-2-azide glucose derivatives 4 can be obtained from “locked-ring” glucals 3 with satisfactory selectivity.² Based on the high reactivity of radical and antiparallel addition products, empirical analysis suggested that allylic 1,2-strain may lead to the kinetic addition. However, other “unlocked-ring” glucals only provided equatorial addition products with poor selectivity.³ These results are contrary to the previous hypothesis. Until now, due to the poor selectivity, axial addition products (ManNAc derivatives) haven't been obtained by this method. In this report, we intend to explain the selectivity of azide radical addition in these cases with “armed and disarmed” theory.

Scheme 1 The synthesis of hexosamines from glycals.

The addition of azide radical to glucals 3 showed that bulky substituents on C3 of “lock-ring” glucal enhance the equatorial addition. The result of molecular modelling of glucal 3b shows that the substitution group on C3 adopts a parallel position with the olefin plane. Furthermore, it has been reported that interactions between substituents on oxygen atoms could dramatically impact the low energy conformations of glucals.⁴ Hence, it is reasonable to surmise that torsional strain may play a decisive role on the selectivity instead of allylic 1,2-strain. Specifically, the above results sustained that the torsional strain contributed by dihedral angel assigned in red (Scheme 1) facilitated the equatorial addition. This observation propelled us to envisage that substrates bearing bulky substituents on the C4 and C6 (highlighted with green) would be prone to undergo the axial addition. Unsurprisingly, as showned in Table 1, the desired axial addition products were obtained in the initial attempts (entries 1 and 2) with moderate selectivity. A significant raise in selectivity was realized in entry 3. As can be seen, the glucal 5c with a TBDPS group on C6 and a benzyl group on C4 provided the axial face addition product 6c in 15 : 1 dr. In entry 4, glucal 5d, which had more bulk on C4 than glucal 5c provided the axial face addition product 6d exclusively. The high selectivity of above results sustained the dramatic effect of torsional strain on the selectivity. The axial selective addition was also obtained in entry 5. In this case, a hydrogen bond between the hydroxyl group and acetyl group on C4 of the glucal 5e was supported to result in the highly selective axial addition product 6e. The poor selectivity of entry 6 further supported this assumption.

Table 1 The synthesis of ManNAc derivatives with glucals^a

Entry	Substrates 5	Products (dr)^b (6, 7)	Time (h)	Yield^b
a The reaction was typically performed by addition of 3 equiv. of CAN portion-wise to a solution of 1.5 equiv. of NaN3 and 1 equiv. of glycal at −25 °C.b The ratio of two diastereoisomers is determined by ^1H NMR.
1		6a, 7a (2 : 1)	1.5	75%
2		6a, 7b (4 : 1)	4	82%
3		6c, 7c (15 : 1)	1.5	72%
4		6d	2	75%
5		6e	6	80%
6		6f, 7f (1 : 2)	6	40%

---

To further illustrate the mechanism, the relative energy of substrates, transition states, intermediates were studied by Gaussian 09.⁵ Exhausted conformational search was performed to locate the most stable geometries of compounds 5c, 5e, 3b and relative species (see ESI† for details). Then, gas-phase geometry optimization was computed using the B3LYP/6-31G(d) method, and further solvation free energy correction in acetonitrile (SMD single point calculation) was computed using the X3LYP/6-311+G(d,p) method.⁶ These methods were verified to be reliable to work on radical species.

As shown in the Fig. 1, the axial addition of glucal 5c need lower activation energy than the equatorial addition (10.9 kcal mol⁻¹ vs. 9.8 kcal mol⁻¹), and the intermediate of equatorial addition is slightly more stable than the axial one. Therefore, the axial addition should be preferred kinetically. We also stimulated the energy profile of glucal 3b. The predominant equatorial addition product 4b was proved to be preferred in kinetic process (10.3 kcal mol⁻¹ vs. 7.0 kcal mol⁻¹). Furthermore, our theoretical ratio was consistent with the experimental result (see ESI† for details). These data thus verified our previous postulate.

Fig. 1 Free energy profile of glucal 5c, 3b and relative species.

For glucal 5e and relative species, the conformation with the hydrogen bond (shown in Fig. 2) was found to be more stable than any other conformations. Free energy pathways based on this conformation are shown in Fig. 1. Surprisingly, compared with the equatorial addition, the axial addition required nearly the same activation energy but offer the more thermodynamically stable intermediate (9.2 kcal mol⁻¹ vs. 6.7 kcal mol⁻¹). Hence, alcohol 6e is the thermodynamic favored product. To confirm the reversibility of azide radical addition intermediates, an intermediate was obtained with bromide glycoside and hexa-n-butylditin by thermolysis (Scheme 2). The proposed glucal produced by reverse reaction was isolated from the mixture with 25% yield.

Fig. 2 Free energy profile of glucal 5e and relative species.

Scheme 2 The reversibility of azide radical addition.

In order to reveal the relationship between electronic property with reactivity, average local ionization energy was calculated to estimate the oxidizability of radical atom C1 in radical intermediates of 5c, 5e and 3b. As shown in the Fig. 3, the average local ionization energy of intermediates of 5e is larger than intermediates of 5c and 3b, meaning that the intermediates of 5e is more stable than its counterparts. “Armed and disarmed” theory, which was first established by Fraser-Reid and coworkers in 1988,⁷ usually used to interpret the reactivity of glycosyl donors. In glycosylation reactions, “armed” donors bearing electron-donating groups on C4 and C6 was more reactive than “disarmed” ones. In this report, the evidence suggested this theory was also instructive to the reactivity of radical on the C1. The acetyl group and hydrogen bond of glucal 5e decreased the electron density on the C1 and make the radical relatively inert to further oxidize. And also, the glucals are more stable than their intermediates. These properties made the reverse reaction possible.

Fig. 3 The average local ionization of intermediates.

Herein, we also provided a convergent route to C9 modified neuraminic acids based on our discovery (Scheme 3). The strategy was initiated by the synthesis of ManNAc derivative 10 with alcohol 6e via substitution, catalytic hydrogenation, acetylation and deprotection. The trisaccharide 12 was synthesized using E. coli K-12 sialic acid aldolase, N. meningitides CMP-sialic acid synthetase (NmCSS) and Photobacterium damsela α-2,6-sialyltransferase (Pd2,6ST) from sodium pyruvate, CTP, disaccharide 11 and compound 10 in 80% yield, according to Chen's one pot three enzymes procedure.⁸ This kind of neuraminic acids have proved to be ligands of CD22 (Siglec-2) and have potential therapeutic utilities in B cells correlated diseases.⁹

Scheme 3 The synthesis of C9 modification neuraminic acid derivative 12 from 6e.

Conclusions

In conclusion, to the best of our knowledge, this is the first report about stereoselectively synthesis of ManNAc derivatives with glucals. And we showed a potential application of our method in the chemo-enzymatic synthesis of neuraminic acid derivatives. Experimental results and systematic high accuracy computational studies revealed that “armed” glucals, as “armed” donors in glycosylation, are more reactivity in the radical addition and prone to offer kinetic-controlled products. In the kinetic process, torsional strain plays a decisive role in the selectivity by influencing the relative energies of diastereomeric transition state. And “disarmed” glucals are relatively inertia in the reaction. Due to this property thermodynamic stable diastereoisomer could be accessed as predominant product. We hope our discovery has positive impacts in the understanding the property of radical in the ring system.

Acknowledgements

We thank the Natural Science Foundation of China (21332006, 21372130, 31170768) and Natural Science Foundation of Tianjin (12JCYBJC18600, 13ZCZDSY00600) for financial support.

Notes and references

1. (a) S. Wagner, C. Mersch and A. Hoffmann-Roder, Chem.–Eur. J., 2010, 16, 7319–7330; (b) S. A. Svarovsky and J. J. Barchi, Carbohydr. Res., 2003, 338, 1925–1935; (c) O. Srinivas, B. Muktha, S. Radhika, T. N. G. Row and N. Jayaraman, Carbohydr. Res., 2004, 339, 1447–1451; (d) L. K. Shi-Shun, J. M. Mallet, M. Moreau and P. Sinay, Tetrahedron, 1999, 55, 14043–14068; (e) N. Shao and Z. W. Guo, Org. Lett., 2005, 7, 3589–3592; (f) O. Renaudet and P. Dumy, Tetrahedron Lett., 2004, 45, 65–68; (g) R. Pragani, P. Stallforth and P. H. Seeberger, Org. Lett., 2010, 12, 1624–1627; (h) S. A. Mitchell, M. R. Pratt, V. J. Hruby and R. Polt, J. Org. Chem., 2001, 66, 2327–2342; (i) R. U. Lemieux and R. M. Ratcliffe, Can. J. Chem., 1979, 57, 1244–1251; (j) D. J. Lee, P. W. R. Harris, R. Kowalczyk, P. R. Dunbar and M. A. Brimble, Synthesis-Stuttgart, 2010, 763–769; (k) S. Danishefsky and M. Barbachyn, J. Am. Chem. Soc., 1985, 107, 7761–7762.
2. P. H. Seeberger, S. Roehrig, P. Schell, Y. Wang and W. J. Christ, Carbohydr. Res., 2000, 328, 61–69.
3. (a) E. Saxon, S. J. Luchansky, H. C. Hang, C. Yu, S. C. Lee and C. R. Bertozzi, J. Am. Chem. Soc., 2002, 124, 14893–14902; (b) G. C. Look, Y. Ichikawa, G. J. Shen, P. W. Cheng and C. H. Wong, J. Org. Chem., 1993, 58, 4326–4330; (c) S. Lee and J. P. N. Rosazza, Org. Lett., 2004, 6, 365–368; (d) M. Forsgren and T. Norberg, Carbohydr. Res., 1983, 116, 39–47.
4. (a) M. Rico and J. Santoro, Org. Magn. Reson., 1976, 8, 49–55; (b) D. Horton, W. Priebe and O. Varela, XII Int. Carbohydrate Symposium, Utrecht, 1984; (c) A. A. Chalmers and R. H. Hall, J. Chem. Soc., Perkin Trans. 2, 1974, 6, 728–732.
5. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, M. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, D. J. Fox and I. Gaussian, R. D. Gaussian 09, Wallingford CT, 2009.
6. (a) X. Xu and W. A. Goddard, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2673–2677; (b) M. Bittererova, H. Ostmark and T. Brinck, J. Chem. Phys., 2002, 116, 9740–9748.
7. (a) L. K. Mydock and A. V. Demchenko, Org. Lett., 2008, 10, 2103–2106; (b) X. Y. Liang, H. C. Bin and J. S. Yang, Org. Lett., 2013, 15, 2834–2837; (c) B. Fraser-Reid, K. N. Jayaprakash, J. C. Lopez, A. M. Gomez and C. Uriel, ACS Symp. Ser., 2007, 960, 91–117.
8. H. Yu, S. S. Huang, H. Chokhawala, M. C. Sun, H. J. Zheng and X. Chen, Angew. Chem., Int. Ed., 2006, 45, 3938–3944.
9. (a) C. D. Rillahan, E. Schwartz, R. McBride, V. V. Fokin and J. C. Paulson, Angew. Chem., 2012, 51, 11014–11018; (b) C. M. Nycholat, C. Rademacher, N. Kawasaki and J. C. Paulson, J. Am. Chem. Soc., 2012, 134, 15696–15699; (c) W. C. Chen, G. C. Completo, D. S. Sigal, P. R. Crocker, A. Saven and J. C. Paulson, Blood, 2010, 115, 4778–4786.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra00296f

‡ These authors contributed equally to the work.

---