Enhanced thermoelectric performance of BiSbTe-based composites incorporated with amorphous Si3N4 nanoparticles
Y. C. Dou,
X. Y. Qin*,
D. Li,
Y. Y. Li,
H. X. Xin,
J. Zhang,
Y. F. Liu,
C. J. Song and
L. Wang
and
L. Wang
Key Laboratory of Materials Physics, Institute of Solid State Physics Chinese Academy of Sciences, 230031 Hefei, P. R. China. E-mail: xyqin@issp.ac.cn; Fax: +86 0551 65591434; Tel: +86 0551 65592750
First published on 8th April 2015
Abstract
Thermoelectric properties of BiSbTe-based composites dispersed with a small amount (<1 vol%) of amorphous Si3N4 (a-Si3N4) nanoparticles (∼25 nm) were investigated in the temperature range from 303 K to 483 K. The results indicate that with a-Si3N4 content increasing, the thermopower (S) of the a-Si3N4/BiSbTe composites increases substantially at T < ∼370 K, due to the decreased carrier concentrations and the enhanced energy-dependent scattering of the carrier at the heterojunction potential. Simultaneously, a-Si3N4 nanodispersion causes ∼20–30% reduction in thermal conductivity (κ) owing to phonon scattering of nanoparticles as well as phase boundaries. As a result, high dimensionless figure of merit (ZT) values of up to 1.20 (∼303 K) and 1.38 (∼383 K) are obtained in Bi0.4Sb1.6Te3 incorporated with only 0.44 vol% a-Si3N4 nanoparticles, demonstrating that the thermoelectric performance of the BiSbTe alloy can be improved effectively through incorporation of a-Si3N4 nanoparticles.
Introduction
Thermoelectric (TE) materials have attracted increasing attention owing to their potential applications in energy conversion and power generation.1 The efficiency of TE materials is characterized by the dimensionless figure of merit ZT, which is defined as ZT = S2σT/κ (κ = κL + κC), where S, σ, κ, (κL, κC) and T are the Seebeck coefficient (or thermopower), electrical conductivity, thermal conductivity (the lattice κL and carrier κC contributions), and absolute temperature respectively.2,3 It is clear that there are usually two ways to improve ZT: one is to boost the power factor PF (S2σ) and the other is to reduce thermal conductivity (κ). Although there have been persistent efforts to improve ZT values since the 1950s, ZT of the best commercial materials has remained 1 mainly due to the interdependence of the parameters involved in ZT.4 However, with the development of experimental and theoretical innovation several successful examples have been reported recently, in which remarkable advances in ZT can be realized by decoupling the electrical and thermal transport properties.5–8 Up to now, the main approach is to introduce different nanostructures into bulk TE materials by in situ precipitation or incorporation of nanoparticles, in which phonons are effectively scattered while the scattering of conducting electrons is minimized. For instance, enhanced thermoelectric properties have been achieved in both p-type and n-type half-Heuslers by Ren et al.9 In fact, the notable improvement in ZT value, benefited from the formation of half-Heusler nanocomposite through a high energy ball milling.9,10 Obviously, the significant increase of Seebeck coefficient and the remarkable reduction of phonon thermal conductivity are believed to be due to quantum effect11/energy filtering effect12 at the interface and size effect of the nanostructures, respectively, thereby providing a significant ZT enhancement.Bi2Te3-based alloys are the state-of-the-art thermoelectric materials that are (uniquely) used commercially at near room temperature for refrigeration. Numerous researches have been performed to improve their ZT by structural and composition modification since Bi2Te3-based alloys were found in 1960s.13–18 Especially, the ZT value as high as 1.4 (at ∼373 K)17 or even 1.50 (at ∼390 K)18 was reported in p-type BixSb2−xTe3 with nanostructures. Previous studies, such as D-ATP/BiSbTe19 (ZTmax = 1.3 at 420 K), SiC/BiSbTe20 (ZTmax = 1.33 at 373 K), indicated that incorporating nanoparticles into BiSbTe matrix could bring positive impact on improving its ZT.
In order to reduce lattice thermal conductivity and enhance thermopower of BiSbTe system, small amounts (<1 vol%) of amorphous Si3N4 (a-Si3N4) nanoparticles (∼25 nm) were incorporated into BiSbTe matrix to form nanocomposites in the present work. Nanometer sized a-Si3N4 (∼25 nm) is a kind of insulator that can form fine dispersed nanophase in BiSbTe matrix, and phase boundaries and the heterojunction potential are expected to be formed in the composite system, which could be beneficial to enhancing both phonon scattering and selective carrier scattering, respectively. Besides, as a constituent of the composite system, the disordered amorphous structure of a-Si3N4 could lead to a further thermal conductivity reduction by enhancing phonons scattering due to the extremely small mean free paths of phonons in a-Si3N4. As expected, our results show that incorporating a-Si3N4 nanoparticles into the p-type BiSbTe matrix is effective for its thermoelectric property enhancement. Specifically, incorporation of only 0.44 vol% a-Si3N4 nanoparticles into Bi0.4Sb1.6Te3 alloy results in remarkably decrease in thermal conductivity (κ), leading to higher dimensionless figure of merit (ZT) value of up to 1.20 (∼303 K) and 1.38 (∼383 K), respectively. Present results suggest that incorporation of amorphous nanoparticles into BiSbTe-based alloys be an effective way to enhancing their thermoelectric performance.
Experimental procedures
Elemental powders Bi (99.99%, Alfa Aesar), Sb (99.5%, Sigma Aldrich) and Te (99.999%, Alfa Aesar) granules were weighted according to the formula of Bi0.4Sb1.6Te3 doped with 3 wt% Te. The powder mixture was loaded into quartz ampoule sealed under vacuum at 10−2 Pa, and then heated to 800 °C for 24 h. Then the ingot was grinded into powders. These powders were subjected to ball milling process with the compositions of Bi0.4Sb1.6Te3 (BiSbTe) and blended with a volume fraction f (f = 0, 0.22, 0.44, 0.88 vol%) of commercial a-Si3N4 nanoparticles (the purity is ≥99.0 atm% and mean particle size is ∼25 nm) in a planetary ball mill at 150 rpm for 6 h in a purified argon atmosphere. Stainless steel vessels and agate balls were used. The weight ratio of ball to powder was kept at 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Proper ethyl alcohol was needed in order to gain good dispersed composites. After oven dry, the ball-milled powders were compacted by spark plasma sintering under a pressure of 50 MPa in a diameter of 20 mm graphite mold in vacuum for 5 min. The sintering temperature and heating rate were 673 K and 323 K min−1, respectively. Disks of 10 mm in diameter and 2 mm thick were then obtained. The phase structure was studied by X-ray diffraction at room temperature using Cu Ka radiation. The fractographs were observed by field emission scanning electron microscopy (FE-SEM). The compositions of the composites were confirmed by using energy dispersive analysis system of X-ray (EDX) equipped in FE-SEM.
1. Proper ethyl alcohol was needed in order to gain good dispersed composites. After oven dry, the ball-milled powders were compacted by spark plasma sintering under a pressure of 50 MPa in a diameter of 20 mm graphite mold in vacuum for 5 min. The sintering temperature and heating rate were 673 K and 323 K min−1, respectively. Disks of 10 mm in diameter and 2 mm thick were then obtained. The phase structure was studied by X-ray diffraction at room temperature using Cu Ka radiation. The fractographs were observed by field emission scanning electron microscopy (FE-SEM). The compositions of the composites were confirmed by using energy dispersive analysis system of X-ray (EDX) equipped in FE-SEM.
Bars of about 2 × 2 × 10 mm and disks of 9 mm in diameter and 2 mm thick were cut from the pressed disks and polished for the thermoelectric properties characterization. The electrical resistivity and the Seebeck coefficient were measured simultaneously by commercial equipment (ULVAC-RIKO: ZEM-3, Japan) under He atmosphere from 303 to 483 K. Hall coefficient was measured at 303 K by applying a field of 250 mT, and the carrier concentrations and mobility were calculated by using Hall coefficient and electrical resistivity. The thermal diffusivity, D, was measured using the laser flash method (Netzsch, LFA 457). The specific heat, Cp, was determined by a commercial instrument (Pyris Diamond DSC, Perkine Elmer). The density, γ, was measured by the Archimedes method. The resulting total thermal conductivity was calculated from the measured thermal diffusivity D, specific heat Cp, and density γ from the relationship κ = DγCp.
Results and discussion
Microstructural characterization
Fig. 1 shows the XRD patterns of f(a-Si3N4)/BiSbTe (f = 0, 0.22, 0.44 and 0.88 vol%) composite powders. The diffraction peaks of Si3N4 powder are shown in the inset of Fig. 1, revealing that Si3N4 nanoparticles are amorphous. All the main diffraction peaks in the XRD patterns of f(a-Si3N4)/BiSbTe composites are consistent with the standard JCPDS (PDF#01-072-1836) card of Bi0.4Sb1.6Te3 with rhombohedral structure (crystal group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). As compared with the pattern of BiSbTe, no obvious changes are observed in XRD patterns for f(a-Si3N4)/BiSbTe composites, for the dispersed a-Si3N4 nanoparticles have amorphous structure which cannot give rise to any diffraction peak. The SEM images and the electron energy spectrum obtained by using EDX for 0.44 vol% a-Si3N4/BiSbTe composite sample are shown in Fig. 2. As shown in Fig. 2(a), the grain size of BiSbTe powder range from around 0.2 μm to 2 μm, and some very small white grains existed. The vertical and horizontal cross-sections of scanning electron micrographs of the 0.44 vol% a-Si3N4/BiSbTe composite sample are given in Fig. 2(b) and (c), respectively. It can be seen that fine-grained microstructure can be expected due to the low sintering temperature and fast sintering process of SPS technique. Moreover, one can observe some very small white particles distributed homogeneously in BiSbTe matrix, indicating that a-Si3N4 nanoparticles are successfully incorporated in BiSbTe matrix, forming (a-Si3N4)/BiSbTe bulk composites, which can be confirmed by the electron energy spectrum obtained by using EDX as shown in Fig. 2(d).
m). As compared with the pattern of BiSbTe, no obvious changes are observed in XRD patterns for f(a-Si3N4)/BiSbTe composites, for the dispersed a-Si3N4 nanoparticles have amorphous structure which cannot give rise to any diffraction peak. The SEM images and the electron energy spectrum obtained by using EDX for 0.44 vol% a-Si3N4/BiSbTe composite sample are shown in Fig. 2. As shown in Fig. 2(a), the grain size of BiSbTe powder range from around 0.2 μm to 2 μm, and some very small white grains existed. The vertical and horizontal cross-sections of scanning electron micrographs of the 0.44 vol% a-Si3N4/BiSbTe composite sample are given in Fig. 2(b) and (c), respectively. It can be seen that fine-grained microstructure can be expected due to the low sintering temperature and fast sintering process of SPS technique. Moreover, one can observe some very small white particles distributed homogeneously in BiSbTe matrix, indicating that a-Si3N4 nanoparticles are successfully incorporated in BiSbTe matrix, forming (a-Si3N4)/BiSbTe bulk composites, which can be confirmed by the electron energy spectrum obtained by using EDX as shown in Fig. 2(d).
 | ||
| Fig. 1 XRD patterns of f(a-Si3N4)/BiSbTe composite powders (f = 0, 0.22, 0.44 and 0.88 vol%) and of a-Si3N4 nanoparticles. | ||
Thermoelectric properties
The electrical properties of f(a-Si3N4)/BiSbTe (f = 0, 0.22, 0.44 and 0.88 vol%) composite samples are shown in Fig. 3. As shown in Fig. 3(a), electrical resistivity ρ (1/σ) of all the samples increases with increasing temperature, showing the characteristics of degenerate semiconducting behavior. Since a-Si3N4 is a kind of insulator that has a very high electrical resistivity, ρ of these composites increases with increasing f. Generally, ρ at 303 K increases from 0.892 × 10−3 Ω cm to 1.13 × 10−3 Ω cm, 1.18 × 10−3 Ω cm and 1.22 × 10−3 Ω cm, respectively, as shown in Table 1. The positive values of Seebeck coefficient (S) (Fig. 3(b)) in the whole temperature range mean that the major charge carriers in all the samples are holes. In addition, S for the composite samples was observed to increase with increasing temperature, and after reaching a maximum value it decreases obviously with further increase in temperature. This behavior has been reported previously21 and could be attributed to thermal excitation of minority carriers. Moreover, S generally increases with increasing a-Si3N4 content (f = 0.22, 0.44 vol%) below ∼370 K. Specifically, S for 0.44 vol% a-Si3N4/BiSbTe composite sample at 303 K reaches 207 μV/K, which is higher than that (196 μV K−1) of the BiSbTe matrix. Nevertheless, for the large amount addition of a-Si3N4 (f = 0.88 vol%), S of the composite sample lowers as compared to that of the sample with f = 0.44 vol%.| f | Rh (104 cm3 C−1) | P (1019 cm−3) | μ (cm2 V−1 s−1) | ρ (10−3 Ω cm) | λ |
|---|---|---|---|---|---|
| 0 | 1.42 | 4.41 | 158.9 | 0.892 | 0 |
| 0.22 vol% | 1.43 | 4.35 | 127.1 | 1.13 | 0.07 |
| 0.44 vol% | 1.45 | 4.32 | 122.6 | 1.18 | 0.13 |
| 0.88 vol% | 1.48 | 4.23 | 121.1 | 1.22 | 0.06 |
Hall coefficient measurement indicates that as f increases the carrier concentrations P decreases slightly due to insulator nature of a-Si3N4, as given in Table 1. Simultaneously, the carrier mobility μ declines from 158.9 cm2 V−1 s−1 to 127.1, 122.6, and 121.1 cm2 V−1 s−1 with increasing f, due to enhanced interface scattering. Hence, it is clear now that the increase of ρ is caused by the decrease of both P and μ in the composites. Generally, for degenerate semiconductors S can be expressed by the Mott equation, as following:
 | (1) |
 | (2) |
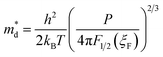 | (3) |
 | (4) |
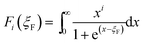 | (5) |
As shown in Fig. 3(d), the maximum value of power factor (PF) of 43 μW cm−1 K−1 is obtained for the BiSbTe matrix at 303 K, and PF of all the samples decreases with increasing temperature. Moreover, the PF values of these composite samples decrease with increasing f. For instance, When f increases to 0.44 vol%, its PF decreases to 35.7 μW cm−1 K−1 at 303 K, which is almost 17% lower than that of the BiSbTe matrix. The decrease in PF mainly comes from reduction in σ (1/ρ).
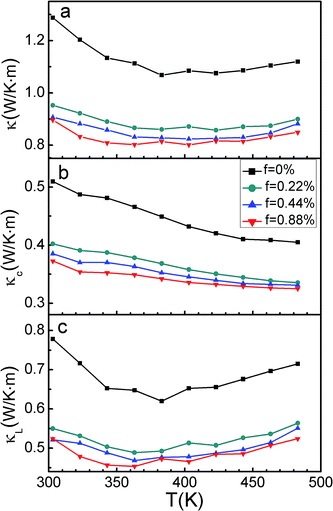
Fig. 4 shows that the temperature dependence of the total thermal conductivity (κ), the carrier thermal conductivity (κC) and the lattice thermal conductivity (κL) for f(a-Si3N4)/BiSbTe (f = 0, 0.22, 0.44 and 0.88 vol%) composite samples, respectively. One can see from Fig. 4(a), the temperature behavior of the total thermal conductivity for the four samples is similar: it decreases with increasing temperature and then increases with further increasing temperature. Moreover, κ for all the composite samples is smaller than that of the BiSbTe matrix and decreases with increasing f in the whole temperate range. Specially, κ for 0.44 vol% a-Si3N4/BiSbTe is reduced to 0.91 W K−1 m−1 at 303 K, which is about 30% lower than that (1.29 W K−1 m−1) of the BiSbTe matrix. The total thermal conductivity consists of a lattice thermal conductivity κL and a contribution of mobile charge carriers, κC, i.e., κ = κL + κC. Usually, κC can be estimated by the Wiedemann–Franz law  , where L0 = 1.5 × 10−8V2/K2 is the Lorentz number, which is obtained from fitting the Seebeck data to the reduced chemical potential,19,26 T is the temperature in Kelvin. As shown in Fig. 4(b), κC in the whole temperature range investigated decreases with increasing f, which is originated from the increase in ρ. By comparison of Fig. 4(c) with Fig. 4(a), one finds that the smaller total thermal conductivity with increasing f originates mainly from the reduction in its lattice thermal conductivity κL. It can be seen that κL decreases monotonically with increasing f in the whole temperate range, which can be attributed to enhanced phonon scattering by the incorporated nanoparticles and the phase boundaries. Specifically, κL of f(a-Si3N4)/BiSbTe (f = 0.44 vol%) at 303 K reaches 0.52 W K−1 m−1, which is around 33% lower than that (0.78 W K−1 m−1) of the BiSbTe matrix. However, the increase in κL with temperature at T > ∼363–483 K could be ascribed to the ambipolar contribution due to the increasing intrinsic excitation. In the intrinsic conduction region for narrow-band-gap semiconductors, such as BiSbTe system, a considerable contribution to the thermal conductivity is made by the component due to the ambipolar diffusion of electrons and holes.27 In this case, the total thermal conductivity κ is given by κ = κL + κC + κbi (ambipolar contribution); then at high temperatures (T > ∼363–483 K) κ − κC = κL + κbi, which suggest κL shown in Fig. 4(c) included contribution of κbi.
, where L0 = 1.5 × 10−8V2/K2 is the Lorentz number, which is obtained from fitting the Seebeck data to the reduced chemical potential,19,26 T is the temperature in Kelvin. As shown in Fig. 4(b), κC in the whole temperature range investigated decreases with increasing f, which is originated from the increase in ρ. By comparison of Fig. 4(c) with Fig. 4(a), one finds that the smaller total thermal conductivity with increasing f originates mainly from the reduction in its lattice thermal conductivity κL. It can be seen that κL decreases monotonically with increasing f in the whole temperate range, which can be attributed to enhanced phonon scattering by the incorporated nanoparticles and the phase boundaries. Specifically, κL of f(a-Si3N4)/BiSbTe (f = 0.44 vol%) at 303 K reaches 0.52 W K−1 m−1, which is around 33% lower than that (0.78 W K−1 m−1) of the BiSbTe matrix. However, the increase in κL with temperature at T > ∼363–483 K could be ascribed to the ambipolar contribution due to the increasing intrinsic excitation. In the intrinsic conduction region for narrow-band-gap semiconductors, such as BiSbTe system, a considerable contribution to the thermal conductivity is made by the component due to the ambipolar diffusion of electrons and holes.27 In this case, the total thermal conductivity κ is given by κ = κL + κC + κbi (ambipolar contribution); then at high temperatures (T > ∼363–483 K) κ − κC = κL + κbi, which suggest κL shown in Fig. 4(c) included contribution of κbi.
Based on the data obtained above, Fig. 5 gives the ZT values for f(a-Si3N4)/BiSbTe (f = 0, 0.22, 0.44 and 0.88 vol%) composite samples as functions of temperature. It can be seen that ZT values of all the samples increase with increasing temperature, and after reaching a maximum value ZT decreases with further increasing temperature. Moreover, with increasing a-Si3N4 content to f = 0.22 and 0.44 vol%, ZT increase significantly. Nevertheless, for the large amount addition of a-Si3N4 (f = 0.88 vol%), ZT of the composite sample lowers as compared to that of the sample with f = 0.44 vol%, due to its much smaller PF. Overall, ZT for all the composite samples is larger than that of the BiSbTe matrix in the whole temperate range. Specifically, ZT of the composite sample with f = 0.44 vol% is 1.20 at 303 K, larger than that (1.01) of BiSbTe matrix in the present study; its maximum ZT reaches 1.38 at 383 K. The large enhancement of ZT for all the composite samples originates from the significantly reduced thermal conductivity and enhanced energy filtering effect owing to incorporation of a-Si3N4 nanoparticles.
 | ||
| Fig. 5 ZT values with temperature for f(a-Si3N4)/BiSbTe composite samples (f = 0, 0.22, 0.44 and 0.88 vol%). | ||
Conclusions
Composites f(a-Si3N4)/BiSbTe (f = 0, 0.22, 0.44 and 0.88 vol%) were prepared, and their thermoelectric properties were studied at temperatures from 303 to 483 K. The results indicate that although electrical resistivity increases with increasing a-Si3N4 content due to the decrease in both carrier concentrations and carrier mobility, Seebeck coefficient increases substantially at T < ∼370 K owing to decrease in carrier concentrations and increase in scattering parameter. Specially, incorporation of a-Si3N4 nanoparticles into BiSbTe significantly reduces the thermal conductivity of composite samples due to enhanced phonon scattering by the nanoparticles and the phase boundaries. As a result, ZT of f(a-Si3N4)/BiSbTe with f = 0.44 vol% reaches 1.20 at 303 K (which is larger than that (1.01) of BiSbTe matrix in the present study), and specifically its maximum ZT reaches 1.38 at 383 K, which is round 8% larger than that (1.28) of BiSbTe matrix. Present results suggest that incorporation of amorphous nanoparticles into thermoelectric materials, such as BiSbTe-based alloys, be an effective way to enhancing their thermoelectric performance.Acknowledgements
Financial support from the National Natural Science Foundation of China (nos 11374306, 11174292, 51101150, 50972146, and 10904144) are gratefully acknowledged.Notes and references
- D. M. Rowe, CRC Handbook of Thermoelectrics, CRC Press, LLC, 1995 Search PubMed.
- T. M. Tritt, Semiconductors and semimetals, recent trends in thermoelectric materials research:part one to three, Aca-demic, San Diego, CA, 2000 Search PubMed.
- G. J. Snyder, Appl. Phys. Lett., 2009, 94, 102111 CrossRef PubMed.
- T. C. Harman, P. J. Taylor, M. P. Walsh and B. E. LaForge, Science, 2002, 297, 2229 CrossRef CAS PubMed.
- A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2009, 2, 466 CAS.
- M. S. Dresselhaus, G. Chen, M. Y. Tang, R. Yang, H. Lee, D. Wang, Z. F. Ren, J. Fleurial and P. Gogna, Adv. Mater., 2007, 19, 1043 CrossRef CAS PubMed.
- T. C. Harman, M. P. Walsh, B. E. LaForge and G. W. Turner, J. Electron. Mater., 2005, 34, L19 CrossRef CAS PubMed.
- I. Boukai, Y. Bunimovich, J. Tahir-Kheli, J. K. Yu, W. A. Goddard and J. R. Heath, Nature, 2008, 451, 168 CrossRef PubMed.
- W. S. Liu, X. Yan, G. Chen and Z. F. Ren, Nano Energy, 2012, 1, 42 CrossRef CAS PubMed.
- X. Yan, G. Joshi, W. S. Liu, Y. C. Lan, H. Wang, S. Y. Lee, J. W. Simonson, S. J. Poon, T. M. Tritt, G. Chen and Z. F. Ren, Nano Lett., 2011, 11, 556 CrossRef CAS PubMed.
- T. E. Humphrey and H. Linke, Phys. Rev. Lett., 2005, 94, 096601 CrossRef CAS.
- J. Martin, L. Wang, L. Chen and G. S. Nolas, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 115311 CrossRef.
- R. Venkatasubramanian, E. Siivola, T. Colpitts and B. O'Quinn, Nature, 2001, 413(6856), 597 CrossRef CAS PubMed.
- D. Y. Chung, T. Hogan, P. Brazis and R. L. Melissa, Science, 2000, 287, 1024 CrossRef CAS.
- J. Seo, K. Park, D. Lee and C. Lee, Mater. Lett., 1998, 35, 4 CrossRef CAS.
- C. J. Liu, H. C. Lai, Y. L. Liu and L. R. Chen, J. Mater. Chem., 2012, 22, 4825 RSC.
- B. Poudel, Q. Hao, Y. Ma, Y. C. Chen, A. Minnich, B. Yu, X. Yan, D. Z. Wang, A. Muto, D. Vashaee, X. Y. Chen, J. M. Liu, M. S. Dresselhaus, G. Chen and Z. F. Ren, Science, 2008, 320, 634 CrossRef CAS PubMed.
- W. J. Xie, J. He, H. J. Kang, X. F. Tang, S. Zhu, M. Laver, S. Y. Wang, J. R. D. Copley, C. M. Brown, Q. J. Zhang and T. M. Tritt, Nano Lett., 2010, 10, 3283 CrossRef CAS PubMed.
- T. Zhang, J. Jiang, Y. K. Xiao, Y. B. Zhai, S. H. Yang, G. J. Xu and Z. F. Ren, RSC Adv., 2013, 3, 4951 RSC.
- J. H. Li, Q. Tan, J. F. Li, D. W. Liu, F. Li, Z. Y. Li, M. M. Zou and K. Wang, Adv. Funct. Mater., 2013, 10, 1002 Search PubMed.
- D. H. Kim, C. Kim, S. H. Heo and H. Kim, Acta Mater., 2011, 59, 405 CrossRef CAS PubMed.
- X. H. Yang, X. Y. Qin, J. Zhang, D. Li, H. X. Xin and M. Liu, J. Alloys Compd., 2013, 558, 203 CrossRef CAS PubMed.
- J. P. Heremans, C. M. Thrush and D. T. Morelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(11), 115334 CrossRef.
- T. Caillat, J. P. Fleurial and A. Borshchevsky, J. Phys. Chem. Solids, 1997, 58(7), 1119 CrossRef CAS.
- S. V. Ovsyannikov, Yu. A. Grigor'eva, G. V. Vorontsov, L. N. Luk'yanova, V. A. Kutasov and V. V. Shchennikov, Phys. Solid State, 2012, 54, 261 CrossRef CAS.
- K. Biswas, J. Q. He, I. D. Blum, C. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414 CrossRef CAS PubMed.
- L. D. Zhao, H. J. Wu, S. Q. Hao, C. I. Wu, X. Y. Zhou, K. Biswas, J. Q. He, T. P. Hogan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2013, 6, 3346 CAS.
| This journal is © The Royal Society of Chemistry 2015 |