Hydrogen diffusion in MgH₂ doped with Ti, Mn and Fe

Abstract

Incorporation of suitable dopants in MgH₂ is widely investigated as the way of improving hydrogen storage characteristics of this material. The catalytic role of transition metal dopants on hydrogen desorption from MgH₂ is very promising, but further attention is required in order to optimize the experimental methods and design materials with desired properties. In this paper we investigate the role of Ti, Fe, and Mn on the transport properties of hydrogen in MgH₂, which are marked as limiting factor in the effort to lower the hydrogen desorption temperature. Taking into account the lattice relaxation around the impurities, we consider a number of different diffusion paths in the pure and doped system. Using PAW DFT calculations in combination with the NEB method, we demonstrate that the diffusion of the most relevant positively charged hydrogen vacancy and negatively charged interstitial hydrogen atom is locally hindered by the presence of the impurity atoms.

---

1 Introduction

MgH₂ attracts a lot of attention as one of the most practical solutions for on-board hydrogen storage, which is mainly due to its high hydrogen capacity (gravimetric capacity 7.6 wt%, volumetric capacity 110 g L⁻¹) and low cost.¹ The main obstacles for large scale applications remain the stability of the hydride and its poor kinetic properties. The rate of hydrogen absorption and desorption in the material is relatively low, which can be traced back to the slow diffusion of hydrogen into the rutile crystal lattice of MgH₂.² This, together with the stability of the Mg–H bond, translates into a relatively high temperature of desorption of around 400 °C at ambient pressure.³

Considering MgH₂ as the prototype material for reverse hydrogen storage, ways of tailoring the desired hydrogen storage properties have been proposed. The multi-step process of hydrogen absorption in magnesium is characterized by slow hydrogen sorption kinetics, and its mechanisms are widely studied.^4–6 The present results point to the formation of a MgH₂ layer as the main reason for low absorption rate, given that this layer blocks hydrogen diffusion and further hydrogen uptake in the sample.⁷ Improvement of the hydrogen absorption/desorption kinetics is achieved through shortening the path for hydrogen diffusion (nanostructures, thin films) or by introducing suitable dopants which act as catalysts.^8,9 Transition metal (TM) dopants have been considered good candidates capable of influencing the kinetics of hydrogen absorption and desorption as well as the stability of MgH₂.¹⁰ They are usually incorporated by ball milling and serve as centers for hydride destabilization.¹¹ The catalytic activity of the TM for hydrogen desorption from MGH₂ surface is shown to be large.¹² In addition, TM doping shows beneficial effects on the thermodynamical properties of small MgH₂ clusters.¹³ Directly or indirectly, this is expected to lower the kinetic barriers for hydrogen diffusion in the bulk.¹⁴ However, some puzzling observations remain, one of them being that upon repeated hydrogen desorption/absorption (cycling) in doped MgH₂, the catalytic activity of TM dopants is often shown to decline.¹⁵ Ball-milling also introduces structural defects, reduces crystalline size and induces microstrain,¹¹ therefore enhancing the diffusion of hydrogen in various ways. First principles calculations are widely used to separate the role of ball milling¹⁶ and TM dopants in MgH₂, i.e., to address their effect on stability,^17,18 desorption of hydrogen from surface^12,19 and diffusion in the bulk.²⁰

The diffusion of hydrogen in rutile MgH₂ was studied by Tao et al.¹⁶ Hao et al.²⁰ have found that some dopants can shift the position of the intrinsic Fermi level, thereby altering the population of charged hydrogen defects of interest for hydrogen desorption. Roy et al.²¹ have studied the influence of Ti, Fe, Co and Ni in their interstitial and substitutional configurations on the Fermi level shift and concluded that, in the interstitial configuration, these metals enhance the concentration of hydrogen related defects, while in the substitutional case, a shift of the Fermi energy is not expected. The impact of these dopants is realized via the position of the donor or acceptor levels in the band gap.²¹

However, as the concentration of dopants is increased, it is important to take into account the direct influence of these transition metals on the diffusion of relevant hydrogen defects in their vicinity. Small migration barriers are determined for migration of hydrogen-related defects in rutile MgH₂,²² while, to the best of our knowledge, the direct effect of transition metals on these barriers was not studied. In this work we investigate the diffusion of hydrogen in MgH₂ doped with Ti, Mn and Fe. Hydrogen diffusion in MgH₂ is primarily caused by motion of charged defects;²³ therefore we inspect not only the motion of relevant neutral, but also the motion of charged hydrogen vacancies (V_H) and hydrogen interstitials (H_i) near the dopant site. We find that the substitution of Ti, Mn, and Fe for Mg in the rutile structure of MgH₂ does not improve the rates of diffusion of hydrogen related defects directly, i.e., the diffusion barriers of these defects in the immediate surroundings of the impurities are generally higher than the ones in pure MgH₂. Our calculation shows that the studied transition metals tend to bind hydrogen rather strongly, and thus, suppress its mobility.

2 Computational

Our computational approach is based on the density functional theory (DFT)²⁴ and the projector augmented-wave (PAW) method, as implemented in the Vienna Ab initio Simulation Package (VASP).^25,26 We employed the PW91 generalized gradient functional.²⁷

MgH₂ crystallizes in the rutile structure. As a starting point in our calculations, we relaxed the pure MgH₂ unit cell. The pure structure was relaxed by fitting the total energy of MgH₂ with cubic polynomials on a grid of (a, c) values. All internal degrees of freedom, in the pure and supercell calculations, were relaxed to the nearest local minimum by using the BFGS LineSeach implementation of the Atomic Simulation Environment (ASE) python interface.²⁸ The optimized lattice parameters, a = 4.52 Å and c = 3.02 Å, are in good agreement with the experimental values (4.51 Å and 2.99 Å, respectively).²⁹ The internal parameter that defines the position of hydrogen in the crystal structure was determined to be 0.304.

Starting from the relaxed MgH₂ structure, we constructed a 71 atom 2 × 2 × 3 supercell in which one of the host Mg atoms was replaced with the dopant. The reciprocal space was sampled with a 4 × 4 × 4 k-points, using the tetrahedron method with Blöchl corrections.³⁰ The calculations were spin polarized with cut-off energy of 250 eV. The forces minimization criterion was set to 0.02 eV Å⁻¹. We used a convergence criterion of 1 × 10⁻⁴ eV as the energy difference between two consecutive iterations.

For the calculations of the activation barriers for diffusion, we used the climbing image nudged elastic band (NEB) method.³¹ Our NEB simulations were performed with 7 or 8 images interpolated along the diffusion paths and a spring constant of 0.02 eV Å⁻¹. During the simulation, the forces acting on each of the atoms within the supercell were converged to 0.03 eV Å⁻¹. For the NEB, we used the MDMin optimization algorithm as implemented in the ASE python code.

3 Lattice relaxation

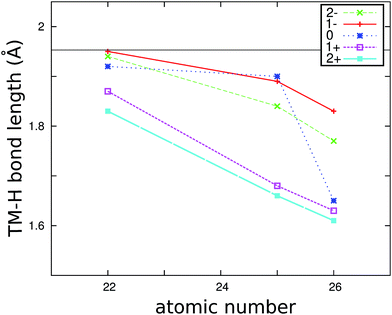
The hydrogen atoms around Mg in pure MgH₂ are approximately arranged in an octahedral fashion. The first coordination shell of Mg is composed out of 6 H atoms divided into two groups: two apical H atoms with Mg–H bonds of 1.94 Å and four equatorial H atoms with Mg–H bonds of 1.96 Å (see Fig. 3). Substitutional transition metals (TM) induce different structural relaxations in MgH₂. After metal replacement, the structures were fully relaxed. Upon substitution and regardless of charge state, we observe a shortening of almost all TM–H bonds as compared to the Mg–H bonds in the pure system. The resulting nearest neighbor TM–H distances for Ti_Mg, Mn_Mg and Fe_Mg, averaged over the first coordination shell, are presented in Fig. 1.

Fig. 1 Calculated average TM–H bond lengths in the first coordination sphere around Ti_Mg, Mn_Mg and Fe_Mg for different charge states of the impurity. The horizontal line denotes the average Mg–H bond length in the pure system.

The shortening of the TM–H bond lengths is most pronounced around the substitutional iron ion. Our calculated Fe–H distances compare well with those obtained in a Car–Parinello Molecular Dynamics study of iron in MgH₂ near the MgH₂–Mg interface.³² We also found a good agreement between our calculated Fe–H and Ti–H distances and the ones calculated by Paskaš Mamula et al.³³

The calculated lattice relaxation around Mn illustrates the need of performing spin polarized calculations. Namely, the lattice relaxation around Mn in its neutral state is markedly different if the spin polarization is switched off, leading to an average Mg–H bond length of only 1.7 Å and a total energy higher by 0.26 eV. In the correct, spin polarized case, Mn is in its high spin state (S = 5/2) and the lattice relaxation of the NN H atoms gives significantly larger bond lengths (∼1.9 Å).

In general, the shorter bond lengths imply that the NN hydrogen atoms are attracted more strongly by the impurity, which, in turn, indicates that the mobility of hydrogen might be hindered with respect to the other parts of the crystal.

4 Defects formation energy

The formation energy of a defect x with charge state q was calculated using the following relation:Here, E_tot is the total energy of the supercell containing the defect, E_tot(bulk) is the total energy of the pure supercell, n_i is the number of atoms of type i added or removed from the system, μ_i is the chemical potential of species of type i and E^ref_i is the reference energy calculated as energy per atom of the corresponding bulk elemental phases. For hydrogen, E^ref is calculated as one half of the total energy of hydrogen molecule. As it can be seen from the formula given above, E_form is a function of the Fermi level position, E_f, within the band gap. E_f is referenced with respect to the top of the valence band E_v, whereas E_c is a correction factor that aligns the electrostatic potential of the defect supercell with that of the defect-free supercell.

For hydrogen desorption in MgH₂, the system should be modeled in the most relevant, hydrogen-poor conditions. In that case, μ_Mg = 0. Given that the stability of MgH₂ implies ΔH_MgH2 = μ_Mg + 2μ_H, we also have μ_H = 1/2ΔH_MgH2, where ΔH_MgH2 is the formation enthalpy of MgH₂. The calculated MgH₂ formation enthalpy is 0.67 eV, which compares relatively well with the experimental value of 0.79 eV.³⁴

The formation energy of intrinsic point defects in MgH₂ under hydrogen-poor conditions is calculated to determine the position of the intrinsic Fermi level; the results are in agreement with earlier report.²² The intrinsic Fermi level, as determined from the charge neutrality of the lowest energy defects (H vacancies), is 2.79 eV. Consequently, the formation energy of V_H⁻ and V_H⁺ is 1.13 eV, while that of the neutral vacancy V⁰_H is 1.10 eV. Given that the formation energies of V_H in all three charge states are close to each other, the concentration of these defects is not expected to play an important role in the overall behavior. The activation energy for diffusion is, therefore, the primary factor that determines the mobility of the vacancy. The formation energies of H_i⁻ and H_i⁺ are 1.35 and 1.86 eV, respectively. In the following, we didn't consider the neutral interstitial hydrogen, H⁰_i, because it is unstable (negative-U center) with a relatively large formation energy of 2.73 eV.

The energies of formation of substitutional Mn, Ti and Fe are presented in Fig. 2. It can be seen that all three impurities have positive-U character and we expect no shift of the intrinsic Fermi level upon doping with these transition metals. Since the TM impurities are stable in their neutral charge state, in the following we are going to consider the kinetic properties of intrinsic defects (H vacancies and interstitials) only with respect to the TM atoms in their neutral charge state.

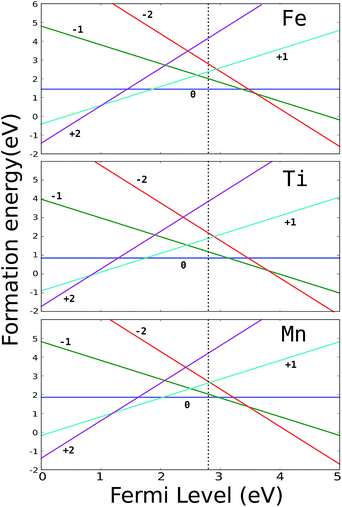Fig. 2 Formation energy of substitutional TM defects in MgH₂. The vertical dotted line represents the intrinsic Fermi level.

5 Diffusion activation energies in pure MgH₂

Regarding the kinetic properties of MgH₂ we first turn our attention to diffusion of variously charged H-related defects in the undoped system.

The activation energy for diffusion is calculated along several different paths in the rutile crystal cell of MgH₂, as depicted in Fig. 3. The path (1 ↔ 2) connects one of the four equatorial hydrogen atoms with one of the two apical hydrogen atoms. The path (1 ↔ 4) connects two neighboring apical H atoms. The path (2 ↔ 3) is parallel to the (1 ↔ 4) path and connects two equatorial atoms. Along (1 ↔ 2) and (2 ↔ 3), the hydrogen vacancy remains bonded to the same central Mg atom (A) at all times, while along (1 ↔ 4), the bond is broken and the defect is transferred to the neighboring Mg atom (B). The path (3 ↔ 4) makes sense only when the central Mg atom (A) is replaced with the impurity, in which case the bond between the defect and the dopant atom is also broken.

Fig. 3 (a) Schematic representation of various diffusion paths in MgH₂: side view (left) and top view (right). (b) Interstitial hydrogen atom in MgH₂.

We have calculated two types of defects: hydrogen vacancies V_H in their neutral, 1+ and 1− charge states (V⁰_H, V_H⁺, and V_H⁻) and hydrogen interstitials H_i in their 1+ and 1− charge states (H_i⁺ and H_i⁻). The diffusion of interstitial hydrogen was considered along the channel in (0,0,1) direction (see Fig. 3) but we also tried some of the directions parallel to the paths described above. This is partly due to the fact that interstitial H in some charge states (1+) builds a strong bond with the nearest H atom (H molecule) and the tetrahedral interstitial site is unstable.

Our calculated diffusion barriers in the pure system are presented in Table 1. We found that the kinetic barrier for migration of hydrogen vacancy is the lowest for V_H⁺ along (1 ↔ 2). Thus, V_H⁺ is also found to be the most mobile vacancy defect in pure MgH₂ with a diffusion barrier of 0.39 eV. This result compares very well to the migration barriers for diffusion of 0.37 eV (ref. 35) and 0.38 eV (ref. 22). On average, V_H⁺ is the most mobile vacancy defect along all of the investigated diffusion paths. The diffusion barrier along (1 ↔ 4) is considerably higher, which is not unexpected given the fact that the defect is no longer attached to the original Mg atom.

Table 1 Calculated diffusion barriers (in eV) along different diffusion paths in the vicinity of substitutional Ti, Mn, Fe and Mg (pure MgH₂). The numbers in parentheses represent the values in the reverse direction in the cases where the diffusion paths are asymmetric

Defect	Path	Mg	Ti	Mn	Fe
VH^+	(1 → 2)	0.39	0.24(0.28)	0.33(0.35)	0.49(0.45)
VH^+	(1 → 4)	0.78	0.50(1.08)	1.07(1.02)	0.38(0.99)
VH^+	(2 → 3)	0.78	0.36	0.61	0.72
VH^+	(3 → 4)	0.39	0.17(0.70)	0.95(0.85)	0.31(0.95)
VH^−	(1 → 2)	1.12	0.54(0.56)	0.19(0.17)	0.07(0.20)
VH^−	(1 → 4)	1.27	0.85(0.96)	1.31(1.22)	1.57(1.24)
V^0H	(1 → 2)	0.75	0.48(0.46)	0.32(0.33)	0.15(0.19)
V^0H	(1 → 4)	0.99	0.55(0.80)	1.34(1.05)	0.96(0.91)
Hi^−	(1 → 2)	0.22	0.28(0.30)	0.68(0.54)	0.6(0.43)
Hi^−	(1 → 4)	0.003	0.003	0.40	2.13
Hi^−	(0,0,1)	0.16	0.34	0.16	1.20
Hi^+	(0,0,1)	0.29	1.74	1.01	1.05

---

Negatively charged interstitial hydrogen, H_i⁻, has a diffusion barrier of 0.16 eV along the central channel in (0,0,1) direction, which compares well to the barrier of 0.15 eV, as calculated by Hao et al.³⁵ H_i⁺, because of its tendency to make a hydrogen molecule with the nearest hydrogen atom,²² doesn't stay in the center of the interstitial channel and has somewhat higher diffusion barrier of 0.29 eV. Interestingly, when H_i⁻ is brought closer to the nearest apical H atoms, we found a very low diffusion barrier. In this configuration [(1 ↔ 4) in Table 1], H_i⁻ pushes the nearest apical H atom away from its original position into the direction of the adjacent interstitial channel and the resulting diffusion barrier is only 0.003 eV. This displacing of the nearest hydrogen atom is similar to the one noticed by Hao et al.²⁰ when considering diffusion in MgH₂ via concerted motions of defects.

From Table 1 we see that on average, H_i⁻ tends to have smaller diffusion barriers than H_i⁻ and therefore it is the most mobile interstitial defect in pure MgH₂.

6 Diffusion activation energies in doped MgH₂

While the diffusion barriers for V_H in the pure system are symmetric, the general feature of the diffusion barriers in the doped system is that they are asymmetric (Fig. 4). That means that the initial and final configuration for the majority of investigated paths have different energies. As a result, the diffusion of V_H is easier either while arriving at or while leaving the impurity.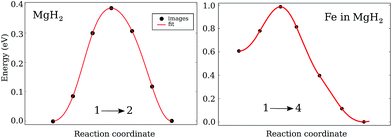

Fig. 4 Migration energy as a function of defect coordinates for V_H⁺ diffusion in Mg₂: left – along (1 → 2) in the pure system; right – along the (1 → 4) path in the Fe doped MgH₂.

Regardless of charge state, the hydrogen vacancy in almost all investigated cases tends to have low diffusion barrier along (1 ↔ 2) and (2 ↔ 3), i.e., when the diffusion is happening in the first coordination shell around the TM atom. It means that once the vacancy is bound to the dopant, its mobility is higher than in the pure system. By contrast, V_H, in most of the cases, tends to have higher diffusion barrier at least in one direction (asymmetric diffusion) along the paths where the bond with the TM atom is broken, e.g., either along (1 → 4) or along (4 → 1).

When we consider the physically most relevant V_H⁺, we see that, e.g., for titanium we have a markedly lower diffusion barrier in (1 → 4) and (3 → 4) direction (0.50 and 0.17 eV, respectively) as compared to the pure system (0.78 and 0.39 eV). At the same time, the barriers are much higher in the opposite [(4 → 1) and (4 → 3)] directions and their calculated values are 1.08 and 0.70 eV. Similar conclusion can be drawn for iron too. Compared to pure MgH₂, this translates into higher diffusion barriers for hydrogen leaving the impurity, and lower diffusion barriers for hydrogen arriving at the impurity. The situation with manganese is somewhat different in the sense that the diffusion barriers near Mn are higher in both directions. Thus, the calculated diffusion barriers suggest that Ti, Fe and Mn serve as centers that locally slow down the diffusion of the most mobile positively charged hydrogen vacancy.

The calculated diffusion barriers for the less mobile V_H⁻ and V⁰_H indicate that in some cases, the diffusion of these defects along some of the paths (e.g., path (1 ↔ 4) for Ti_Mg) might actually be improved, but their impact on the overall hydrogen diffusion in MgH₂ is probably small taking into consideration their stability.

As indicated, in the pure system, negatively charged interstitial hydrogen, H_i⁻, moves along the center of the interstitial channel (Fig. 3(b)). The presence of the impurity atom disrupts this movement and H_i⁻ is strongly attracted toward the raw of atoms where the impurity is located. Except for diffusion of H_i⁻ beside Mn, which gives the same diffusion barrier as in the pure MgH₂, we found that the diffusion barriers close to the other two impurities are higher. The diffusion barriers are also much higher in all the other investigated directions (Table 1). As for H_i⁺, the positively charged interstitial hydrogen in the pure system tends to move by forming a bond with the nearest hydrogen atoms. The TM impurities additionally obstruct this movement and the diffusion barriers in the doped systems are also higher.

The presence of some TM impurities (up to 5 at%) in some specific local configurations has been shown to improve the diffusion of hydrogen in MgH₂ due to the shift in the position of the intrinsic Fermi level.^16,21 Furthermore, for Ti and Fe it was shown that such shifts can be expected only in the case where metals occupy interstitial positions in the MgH₂ lattice, and not when substitution occurs.²¹ The results presented in this work are related to the effect of substitutional TM in the MgH₂ lattice, and therefore they provide a direct insight into the isolated effect of local interaction between the TM and hydrogen-related defects of interest for diffusion.

Our results could explain some puzzling experimental observations, such as that the positive effects of TM doping, primarily related to lowering of hydrogen desorption temperature, were found to decline with cycling¹⁵ or increased concentration of TM dopants in MgH₂.³⁶ The calculated activation energies for the various diffusion paths close to the TM impurity in MgH₂ show that doping with Ti, Mn and Fe could influence the overall hydrogen diffusion in a negative way. With increased doping concentration, the transport properties of the hydrogen related defects close to the impurity site become more important. Therefore, our results suggest that larger concentrations of these transition metals in the MgH₂ crystal cell as well as synthesis methods that favor substitutional TM implementation, should not be expected to improve the hydrogen desorption properties of magnesium hydride.

7 Conclusions

In summary, we have reported on the effects of TM doping on the microscopical processes of hydrogen diffusion in MgH₂. The investigated Ti, Mn and Fe dopants induce a sizable inward relaxation of the hydrogen atoms in the nearest shells. In parallel with this structural change, the diffusion of hydrogen vacancies and interstitial H atoms close to the impurities is significantly altered with respect to the undoped system. For the most mobile positively charged vacancy and negatively charged interstitial hydrogen in MgH₂, our calculations suggest that Ti, Mn and Fe serve as centers that locally slow down the diffusion of hydrogen. Our results suggest that the experimental search for suitable ways of introducing TM dopants should be such to avoid substitutional TM incorporation in MgH₂ (i.e., larger concentrations of transition metals in the MgH₂ crystal cell or synthesis methods that favor such TM incorporation in the crystal cell). At the same time, the obtained results might point to one of the reasons why the initial beneficial effect of TM doping on the MgH₂ desorption properties often declines upon cycling.

The results of this study suggest that the reason for the experimentally determined better hydrogen diffusion upon introducing TM additions in MgH₂ should be looked for elsewhere, and not in the nature of TM–H interaction. Some of the possible explanations remain the indirect impact of the dopants on the Fermi level shift and the pure mechanical destabilization of the rutile crystal structure by the dopants.

Acknowledgements

The authors would like to acknowledge the help of the Serbian Ministry of Science and Education, under Grant no. ON171001.

References

1. I. Jain, C. Lal and A. Jain, Int. J. Hydrogen Energy, 2010, 35, 5133–5144.
2. J. Fernndez and C. Snchez, J. Alloys Compd., 2002, 340, 189–198.
3. B. Sakintuna, F. Lamari-Darkrim and M. Hirscher, Int. J. Hydrogen Energy, 2007, 32, 1121–1140.
4. J. Qu, Y. Liu, G. Xin, J. Zheng and X. Li, Dalton Trans., 2014, 5908–5912.
5. A. V. Kuklin, A. A. Kuzubov, P. O. Krasnov, A. O. Lykhin and L. V. Tikhonova, J. Alloys Compd., 2014, 609, 93–99.
6. M. Chen, Z.-Z. Cai, X.-B. Yang, M. Zhu and Y.-J. Zhao, Surf. Sci., 2012, 606, L45–L49.
7. H. Uchida, S. Wagner, M. Hamm, J. Krschner, R. Kirchheim, B. Hjrvarsson and A. Pundt, Acta Mater., 2015, 85, 279–289.
8. A. Grzech, U. Lafont, P. C. M. M. Magusin and F. M. Mulder, J. Phys. Chem. C, 2012, 116, 26027–26035.
9. T. Liu, C. Wang and Y. Wu, Int. J. Hydrogen Energy, 2014, 39, 14262–14274.
10. M. Zhu, Y. Lu, L. Ouyang and H. Wang, Materials, 2013, 6, 4654–4674.
11. J. Huot, G. Liang and R. Schulz, Appl. Phys. A: Solids Surf., 2001, 72, 187–195.
12. J. M. Reich, L.-L. Wang and D. D. Johnson, J. Phys. Chem. C, 2014, 118, 6641–6649.
13. S. A. Shevlin and Z. X. Guo, J. Phys. Chem. C, 2013, 117, 10883–10891.
14. S. Zheng, Z.-P. Li and L. A. Bendersky, ACS Appl. Mater. Interfaces, 2013, 5, 6968–6974.
15. L. Berlouis, E. Cabrera, E. Hall-Barientos, P. Hall, S. Dodd, S. Morris and M. Imam, J. Alloys Compd., 2000, 305, 82–89.
16. S. Tao, W. Kalisvaart, M. Danaie, D. Mitlin, P. Notten, R. van Santen and A. Jansen, Int. J. Hydrogen Energy, 2011, 36, 11802–11809.
17. E. Germn, V. Verdinelli, C. R. Luna, A. Juan and D. Sholl, J. Phys. Chem. C, 2014, 118, 4231–4237.
18. K. Batalovic, J. Radakovic, J. Belosevic-Cavor and V. Koteski, Phys. Chem. Chem. Phys., 2014, 16, 12356–12361.
19. Z. Wang, X. Guo, M. Wu, Q. Sun and Y. Jia, Appl. Surf. Sci., 2014, 305, 40–45.
20. S. Hao and D. S. Sholl, Appl. Phys. Lett., 2009, 94, 171909.
21. A. Roy, A. Janotti and C. G. Van de Walle, Appl. Phys. Lett., 2013, 102, 033902.
22. M. S. Park, A. Janotti and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 064102.
23. A. Borgschulte, J. H. Rector, H. Schreuders, B. Dam and R. Griessen, Appl. Phys. Lett., 2007, 90, 071912.
24. W. Kohn and L. J. Sham, Phys. Rev. [Sect.] A, 1965, 140, A1133–A1138.
25. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
26. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
27. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
28. S. R. Bahn and K. W. Jacobsen, Comput. Sci. Eng., 2002, 4, 56–66.
29. T. Moriwaki, Y. Akahama, H. Kawamura, S. Nakano and K. Takemura, J. Phys. Soc. Jpn., 2006, 75, 074603.
30. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
31. G. Henkelman, B. P. Uberuaga and H. Jnsson, J. Chem. Phys., 2000, 113, 9901–9904.
32. S. Giusepponi and M. Celino, Int. J. Hydrogen Energy, 2013, 38, 15254–15263.
33. B. P. Mamula, J. G. Novaković, I. Radisavljević, N. Ivanović and N. Novaković, Int. J. Hydrogen Energy, 2014, 39, 5874–5887.
34. M. Yamaguchi and E. Akiba, Material Science and Technology, VCH, New York, 1994, vol. 3B, ch. Ternary Hydrides, p. 333.
35. S. Hao and D. S. Sholl, Appl. Phys. Lett., 2008, 93, 251901.
36. P. B. Amama, J. T. Grant, J. E. Spowart, P. J. Shamberger, A. A. Voevodin and T. S. Fisher, J. Mater. Res., 2011, 26, 2725–2734.

---