Impact of particle surface chemistry on the structure and rheological properties of graphene-based particle/polydimethylsiloxane composites†
Abstract
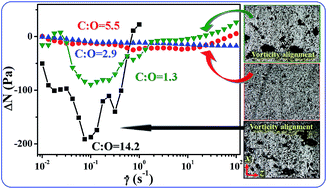
The structure and rheological properties of graphene-based particle (GP-x)/polydimethylsiloxane (PDMS) composites are investigated as the surface oxygen content of graphene-based particle is varied, i.e., from 6.6% (GP-1) to 15.3% (GP-2), 25.5% (GP-3) and 43.1% (GP-4). Interestingly, the dispersion state of graphene-based particles in PDMS does not change monotonically with increasing surface oxygen content. The size of layered stacks and aggregates first decreases from GP-1 to GP-3 and then increases from GP-3 to GP-4 with increasing surface oxygen content. The larger size of layered stacks and aggregates in GP-1 and GP-4 suspensions results from strong inter-particle π–π and hydrogen bonding interactions. Under weak shear, GP-1 and GP-4 form larger aggregates in PDMS, which align along the vorticity direction, inducing negative normal stress differences (ΔN) in the composites. However, GP-2 and GP-3 do not further aggregate under weak shear and the ΔN is almost zero. It is further inferred that the strong inter-particle attractive interaction leads to the vorticity alignment of aggregates under weak shear.

 Please wait while we load your content...
Please wait while we load your content...