Spin rotation driven ferroelectric polarization with a 180° flop in double-perovskite Lu2CoMnO6†
Chao Xina,
Yu Sui*a,
Yi Wang*b,
Yang Wangb,
Xianjie Wanga,
Zhiguo Liua,
Bingsheng Lib and
Xiaoyang Liuc
aDepartment of Physics, Harbin Institute of Technology, Harbin 150001, People's Republic of China. E-mail: suiyu@hit.edu.cn
bNatural Science Research Center, Academy of Fundamental and Interdisciplinary Sciences, Harbin Institute of Technology, Harbin 150080, People's Republic of China. E-mail: yw@hit.edu.cn
cState Key Laboratory of Inorganic Synthesis and Preparative Chemistry, College of Chemistry, Jilin University, Changchun 130012, People's Republic of China
First published on 20th April 2015
Abstract
Structure–property relationships are a key outstanding problem in the study of magnetoelectric multiferroic materials. First-principles calculations were used to explore the influences of Hubbard-U on the ground state of double-perovskite Lu2CoMnO6 as determined by band gap, magnetic moment, spontaneous polarization and structural parameters. The origin of ferroelectricity in the multiferroic Lu2CoMnO6 is elucidated by the calculations of collinear and non-collinear magnetic structure. It is confirmed that the up-up-down-down spin arrangement plays a significant role in the ferroelectric (FE) polarization by the contrast of the lattice geometries and electronic structures in different magnetic orders. The current study shows that both the mechanisms of exchange strictive effects and spin-charge ordering are simultaneously active and lead to the ferroelectric polarization in Lu2CoMnO6. Similar to the early discoveries in HoMnO3 and DyFeO3, we also found and explained the mechanism of switching the ferroelectric polarization via a 180° coherent rotation of Co and Mn spins in double-perovskite Lu2CoMnO6.
I. Introduction
Multiferroic transition metal materials are compounds in which more than one ferroic phases coexist.1 Due to the strong coupling of spin-charge-orbital degrees of freedom,2,3 multiferroics have a lot of fascinating mechanisms in physics and chemistry, and therefore, they have great potential applications in technological areas and have received additional consideration.4–6 The interactions between magnetism and ferroelectricity usually are utilized in the field of sensing applications, as well as in the field of memory devices in which data are typically recorded magnetically and read out electrically. Moreover, with the advent of spin frustrated multiferroics, where-in ferroelectricity is driven by magnetic order rather than non-centrosymmetric crystal structures,7 many novel material systems have come to the fore. However, the ferroelectric polarization in these materials is rather small and the observed magnetoelectric coupling is very weak. Therefore, it is a great challenge to search new gigantic magnetoelectric multiferroic materials. Currently, double-perovskite-type materials are viewed as promising candidates for achieving large magnitudes of induced polarization with ordering temperatures above 40 K.8 The mechanism of magnetoelectric ferroelectric polarization in the double-perovskite oxides such as Y2CoMnO6 (ref. 9) and Y2NiMnO6 (ref. 10) is quite different from that in the spin frustrated perovskite compounds such as CuCrO2 (ref. 11) and hexagonal YMnO3,12 in which the ferroelectric polarization is induced by the non-collinear spin ordering of adjacent magnetic moments. The mechanism of such improper ferroelectricity relates to spin–orbit coupling and is explained by the inverse Dzyaloshinskii–Moria (DM) interaction. However, ferroelectric polarization driven by exchange-striction can be induced by collinear spin ordering and therefore corresponds to double-perovskite oxides. On the basis of such a framework, Lu2CoMnO6 shows large ferroelectric polarization combined with strong magnetoelectric coupling and therefore becomes a very attractive compound.Lu2CoMnO6 belongs to a double-perovskite structure (P21/n space group) with alternating Co and Mn atoms in the B site (in rock-salt order). Both MnO6 and CoO6 octahedrons in the crystal lattice share corners and alternate in CoMnO6 chains along the c direction. The susceptibility measurements of Lu2CoMnO6 has showed that both CoO6 and MnO6 octahedrons contain high-spin Co2+ (d7) and Mn4+ (d3) ions, respectively.13 Powder neutron diffraction shows that the magnetic structure of Lu2CoMnO6 converts to antiferromagnetic (AFM) order at TN = 43 K with a propagation vector k = (0.0224, 0.0099, 0.5). Metamagnetic phase transitions will occur in Lu2CoMnO6 when applying a magnetic field along the c axis, i.e. the ↑↑↓↓ magnetic order will turn to ↑↓↓↓ magnetic order. The polycrystalline specimen exhibits a small magnitude of ferroelectric polarization of ∼2 μC m−2 along the crystallographic c-axis at the lowest temperature, and a broad peak in dielectric constant at 35 K. However, in the single crystals of Lu2CoMnO6, the ferromagnetic order emerges below TC ≈ 48 K along the crystallographic c-axis. At the same time, Lee et al.14 also observed a pronounced peak of the dielectric constant along the crystallographic b-axis at TC, which was inconsistent with the previous observations in the polycrystalline work.13 Thus, the existing experimental data are contradictory and further investigations are still required. In addition, although magnetic phase transitions and the magnetoelectric coupling in Lu2CoMnO6 have been studied by experimental approaches, electronic structure calculations of the double-perovskite Lu2CoMnO6 have not been reported to date. In particular, the driving mechanism of the ferroelectricity has not been investigated by theoretical studies.
In this article, considering the experimentally observed monoclinic structure, we focus on the analysis of the crystal structure and electronic properties to reveal the origin of ferroelectricity in multiferroic Lu2CoMnO6. First, based on accurate collinear magnetic structure calculations and optimized crystal structures, we compared the energy and lattice constants of ↑↑↓↓ type AFM, ↑↓↓↓ ferrimagnetic, ↑↓↑↓ type AFM (A-type), and ↑↑↑↑ ferromagnetic (FM). It is confirmed that ground state magnetic ordering can be affected by the electronic Coulomb repulsion (Hubbard-U). The case of ↑↑↓↓ AFM for Lu2CoMnO6 is discussed within the Heisenberg Hamiltonian. Second, the electronic structure and the bonding in Lu2CoMnO6 are analyzed by GGA + U. Finally, our calculations clarified that the ferroelectric polarization induced by magnetic ordering are explained in detail through spin and lattice degrees of freedom, and an adiabatic path of ferroelectric reversion is provided.
II. Computational details
Our first-principles calculations are based on density functional theory15 as implemented in the Vienna ab initio simulation package (VASP).16,17 We adopt the Perdew–Burke–Ernzerhof functional revised for solids (PBEsol).18 The generalized gradient approximation (GGA)19 with the Hubbard parameter was used to solve the Kohn–Sham equation.20 Compared with the conventional local density approximation (LDA) and GGA, PBEsol has been realized to be quite efficient for GGA + U in describing strongly correlated multiferroic systems.21,22 The simplified, rotationally invariant approach introduced by Dudarev23 was employed by us. The valence configurations used for Lu, Co, Mn and O were 4f145s25p65d16s2, 3d74s2, 3p63d54s2 and 2s22p4, respectively. The plane wave energy cutoff was set to 500 eV (ESI† for more details). For the optimizations of the crystal structure, only the conjugate gradient algorithm24 was used in the current study. Brillouin zone integrations were performed with a tetrahedron method in a 6 × 6 × 2 Monkhorst–Pack25 k-point mesh centered at Γ. The Berry phase method26 with an 8 × 8 × 8 mesh was adopted for calculating the spontaneous polarization (Ps). The ionic positions, lattice parameters and unit-cell shape were sequentially relaxed to obtain the ground state structure in such a way that the external pressure and the residual forces on each atom were less than 0.01 kbar and 0.01 eV Å−1, respectively. Structure, charge density, spin density and ELF visualization and analysis were carried via the VESTA code.27III. Results and discussion
A U dependence of ground state
The crystal structure of Lu2CoMnO6 at room-temperature has the monoclinic space group P21/n (no. 14). As shown in Fig. 1, the conventional unit cell includes four formula units (20 atoms). Neutron-diffraction data taken at T = 4 K shows that Lu2CoMnO6 has an incommensurate antiferromagnetic structure with the wave vector k = (0.0223, 0.0098, 0.5). To satisfy the magnetic structure, we built a 1 × 1 × 2 supercell, which is equivalent to the wave vector. The total energy of the four magnetic structures, the ↑↑↓↓ AFM state, the A-type ↑↓↑↓ AFM state, the ↓↑↑↑ ferrimagnetic state, and the ↑↑↑↑ ferromagnetic state were calculated and are shown in Fig. ESI1 (ESI†). The relative energies of the different magnetic structures for each value of U are listed in Table ESI1.† It is shown that for 2 eV ≤ U ≤ 3 eV, the ↑↑↓↓-type AFM structure possesses the lowest energy. For U ≤ 1 eV, the A-type AFM ↑↓↑↓ structure is stable. For U ≥ 4 eV, the stability of ferromagnetic ↑↑↑↑ structure becomes strong. The U dependence of the various electronic parameters for the ground state of Lu2CoMnO6 is shown in Fig. ESI2.† For U = 0 eV, we obtain metallic solutions in which Co and Mn present localized magnetic moments of 2.27 and 2.85 Bohr magneton (i.e., μCo = 2.27μB, μMn = 2.85μB), respectively. For U = 1 eV, the half-metallic solutions were obtained with 100% spin polarization at the Fermi level, as shown in the Fig. ESI3.† For 2 eV ≤ U ≤ 3 eV, ferromagnetic insulating solutions were obtained in which the band gap (Egap) opens continuously as U increases to U ≥ 4 eV. We also relaxed the structural parameters for the ↑↑↑↑ and ↑↓↑↓ magnetic configuration and compared them to the ↑↑↓↓ state in order to determine the structural distortions induced by magnetic order. Fig. ESI2(c)† shows the U dependence of the Co–O–Mn angles (the Co–O–Mn bond angles in the ac-plane with parallel and antiparallel spins are symbolized αp and αap, respectively), and the αap for ↑↓↑↓ is smaller than the αp for ↑↑↑↑ in the entire U range. However, when both αp and αap are present in the ↑↑↓↓ state, differences are extremely apparent. With the relaxed ionic positions acquired after imposing the ↑↑↓↓ magnetic configuration, the electric polarization (P) was calculated by using the point charge model (PCM) with nominal charges (i.e., −2e for O, +2e for Co, +4e for Mn and +3e for Lu). The U dependence of PPCM is shown in Fig. ESI2(d),† in which PPCM decreases with increase in U. It is known that the FM ↑↑↑↑ and A-type AFM ↑↓↑↓ phase αap do not break inversion symmetry and thus do not allow a ferroelectric polarization to occur. To study the origin of ferroelectric polarization, a range of 2 eV ≤ U ≤ 3 eV should be optimal. At the same time, we also optimized the geometrical structure using different U values. The calculated lattice parameters are a = 5.1367 Å, b = 5.5463 Å and c = 7.3626 Å for UCo = UMn = 2 eV. For UCo = UMn = 3 eV, the lattice parameters are a = 5.1452 Å, b = 5.5431 Å and c = 7.3868 Å, which agree well with the experimental data: a = 5.1638 Å, b = 5.5467 Å and c = 7.4143 Å. Thus, UCo = UMn = 3 eV were chosen for further GGA + U calculations unless mentioned otherwise.When the spin polarization is neglected in our calculations, the results indicate that the structure retains the original P21/n non-polar space group, as observed experimentally at room temperature. After considering spin polarization and antiferromagnetic configuration with magnetic propagation vector k = (0, 0, 1/2), the symmetry lowers from P21/n to the polar space group P21. This means that all the symmetry operations contain time inversion, and that the inversion centre and all mirror planes are broken by the magnetic order. The GGA + U (U = 3 eV) optimized equilibrium lattice constants, corresponding to cell volume, internal atomic coordinates, bond lengths, and bond angles for the double-perovskite-type phase, are listed in Table 1 and Table ESI2.† Such theoretical structural parameters are in good agreement with experimental reports and the theoretical calculation only underestimated the lattice parameter c by 0.38%. There are some differences between the P21 and P21/n configurations, which means that there is a coupling between spin and lattice in this compound. The Wyckoff positions (WPs) of our calculations and the experimental investigations are very similar. However, for the WPs of the P21 structure, there is a small split from the experimental WPs of P21/n. For example, under the P21/n configuration, Mn4+ has one WP (notion c) with four equivalent sites. For the P21 configuration, the four equivalent sites split into two WPs a(1) and a(2), both having two equivalent sites. The minuscule difference between the WPs of experimental structure (P21/n) and calculated structure (P21) lowers the structural symmetry to the polar group. The difference in length between the Co–O and Mn–O bonds manifest a significant cooperative rotation of the CoO6 and MnO6 octahedrons, which was further quantified by the reduction of the Mn–O1–Co (Mn–O2–Co) bond angle, which is predicted to be 141.6° (144.3°) at the GGA + U (UCo = UMn = 3 eV) levels. For UCo = UMn = 5 eV, as we discussed above, the ferromagnetic ↑↑↑↑ structure becomes stable. The structural parameters of Lu2CoMnO6 with ferromagnetic ↑↑↑↑ order are also calculated and the results are presented in Table ESI3.† As represented in Table ESI3,† the calculated structural parameters are very similar with those obtained in the experiment.13 However, the ferromagnetic ↑↑↑↑ ordering does not break the inversion symmetry and thus does not allow a ferroelectric polarization to occur. Therefore, the structure retains the original P21/n non-polar space group.
| Lu2CoMnO6 | GGA + U (P21) | GGA (P21/n) | Expt |
|---|---|---|---|
| a (Å) | 5.1453 | 5.1387 | 5.1638 |
| b (Å) | 5.5431 | 5.4851 | 5.5467 |
| c (Å) | 7.3869 | 7.3292 | 7.4153 |
| V (Å3 per f.u.) | 210.664 | 206.583 | 212.386 |
| Co–O1 (Å) × 2 | 2.0161 | 1.9834 | 2.0274 |
| Co–O2 (Å) × 2 | 2.0531 | 2.0251 | 2.0153 |
| Co–O3 (Å) × 2 | 2.0592 | 2.0411 | 2.0339 |
| Mn–O1 (Å) × 2 | 1.9074 | 1.8873 | 1.8961 |
| Mn–O2 (Å) × 2 | 1.9171 | 1.8926 | 1.9531 |
| Mn–O3 (Å) × 2 | 1.9353 | 1.8922 | 1.9727 |
| Mn–O1–Co (deg) | 141.6 | 141.2 | 141.8 |
| Mn–O2–Co (deg) | 144.3 | 143.4 | 145.5 |
| Mn–O3–Co (deg) | 143.2 | 142.7 | 142.9 |
It is of interest to estimate the nearest-neighbor spin-exchange coupling, especially the three intra-chain spin exchange interactions in the current study, i.e., the super-exchange interaction JCo–Mn between the nearest-neighbor Co2+ and Mn4+ ions, the interaction JCo–Co between the two adjacent Co2+ ions, and the JMn–Mn between the two adjacent Mn4+ ions. The inter-chain interactions are considered as ferromagnetic so as to simplify the analysis. Using the effective Heisenberg Hamiltonian with normalized spin moment,28
 | (1) |
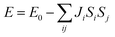 | (2) |
Thus, in terms of the Heisenberg spin Hamiltonian composed of the spin-exchange parameters JCo–Mn, JCo–Co, and JMn–Mn, the corresponding total energy expressions for these four magnetic configurations are given by
| E↑↑↓↓ = −JMn–MnSMnSMn − JCo–CoSCoSCo | (3) |
| E↑↓↓↓ = JMn–MnSMnSMn − JCo–CoSCoSCo | (4) |
| E↑↑↑↑ = 2JCo–MnSCoSMn + JMn–MnSMnSMn + JCo–CoSCoSCo | (5) |
| E↑↓↑↓ = −2JCo–MnSCoSMn + JMn–MnSMnSMn + JCo–CoSCoSCo | (6) |
By subtracting any two of the abovementioned expressions, the values of JCo–Mn, JCo–Co, and JMn–Mn are found to be −2.82 meV, −2.47 meV, and −3.54 meV, respectively. The interaction JCo–Mn is strongly antiferromagnetic because of the very short distance of Co–Mn, which allows indirect metal-O-metal overlap. Within the mean-field approximation, we estimate the transition temperature as follows:
 | (7) |
Here kB is Boltzmann constant. For JCo–Mn = −2.82 meV, we obtain TN = 46 K, which is very close to the measured experimental value TN = 43 K. These results reveal that our GGA + U treatments for spin-exchange interactions of Lu2CoMnO6 are valid and credible.
B Electronic structure and bonding
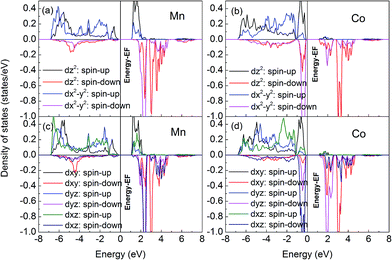
To explain the behavior of spin polarization for Lu2CoMnO6 in the monoclinic phase, the total and partial density of states (DOS) of Lu, O-2p, Co and Mn-3d are shown in Fig. 2. The total DOS of spin-up and spin-down electrons are similar to each other and in accordance with the desired AFM state. The band gap is about ∼1.3 eV, which is evaluated from Fig. 2(a). The energy region near the Fermi level is mainly composed by the 3d states of Co2+ and Mn4+. The energy positions of the O-2p states overlap with those of the Co-3d and Mn-3d states, indicating the hybridization between O-2p and Co, Mn-3d orbitals. The conduction band in the energy range of 5–8 eV are dominated by Lu 4d states.The orbital-resolved DOS of the Co 3d and Mn 3d states in the ↑↑↓↓ AFM are displayed in Fig. 3. The spin-up xy, xz, and yz states of Mn4+ are occupied, and the spin-up z2 and x2 − y2 are also occupied; the occupied states should contribute to the Mn–O–Co superexchange interaction. For each of the xy, xz and yz, states of Co2+, all the up-spin states are occupied, whereas only a small amount of down-spin states (xy) are occupied. For each of the z2 and x2 − y2 states of Co2+, both the spin-up and spin-down states are occupied, and contribute to charge transfer that takes place between the Co and O ions. As a result, the electron configuration of each Co ion is best described as Co2+: (dxy↑, dxz↑, dyz↑)3(dxz↓, dyz↓)2(dz2↑, dx2−y2↑)2, which corresponds to a high-spin Co2+ (d7) ion as anticipated. The five d states reduce degeneracy due to Jahn–Teller distortion, so that the spin-down z2 and x2 − y2 states of Co2+ are occupied. The calculated results give the local magnetic moment of Mn and Co with 3.1μB and 2.6μB, respectively.
To understand the nature of bonding and ferroelectric origin, the charge density and electron localization function (ELF) were calculated by GGA + U. We made a further exploration and calculated the charge density distribution using GGA + U on the (100) principal plane of the supercell. As depicted in Fig. 4(a), the distribution of the charges being along the radius of the circles show that the bonding is ionic, and the charges that asymmetrically surround the O ions are closed to the Mn and Co ions, so the Mn–O and Co–O show covalent bonding nature. However, the properties of bonding determined only from the charge density distribution are not conclusive. The ELF is an informative tool to distinguish the nature of different types of bonds.29 As shown in Fig. 4(b), negligibly small values of the ELF between atoms indicate a dominant ionic bonding character for Mn–O and Co–O. It is shown in Fig. 4(b) that the ELF values reach their maximum at O sites and become very small at the sites of Co and Mn. This is a clear indication of the complete charge transfer that has taken place from the sites of Co/Mn to the sites of O. The metal-to-ligand charge transfer process corresponds to site- and bond-centered charge ordering.6 In contrast, as shown in Fig. 4(b), both the polarization of the ELF between adjacent O sites and the finite ELF value between Lu and O show covalent characteristics to a certain extent. As a result, from the representations of ELF and charge density, we can conclude that both Co–O and Mn–O bonds in Lu2CoMnO6 are mainly ionic in character, and are similar to Fe–O bonds in GaFeO3,30 but different from other proper multiferroics, for example, the mixed properties of ionic and covalent bonding in BiFeO3.31 The short-range repulsion between adjacent closed-shell ions is minimized for symmetric structures. If the bonding between the atoms in BiFeO3 is purely ionic, the structure would remain centrosymmetry (CS) and would not allow a ferroelectric polarization to occur. However, in Lu2CoMnO6, the antiferromagnetic ↑↑↓↓ ordering breaks the inversion symmetry rather than the purely ionic bonding. The nature of bonding can further be verified by the calculation of Born effective charges (the ESI for details, Table ESI4†).
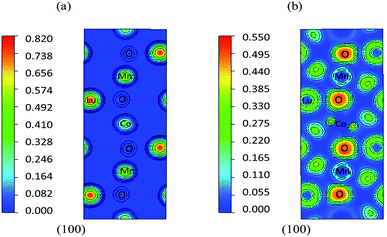 | ||
| Fig. 4 Plots of (a) charge density along (100) principal plane of Lu2CoMnO6 supercell and (b) ELF calculated using the GGA + U method along (100) principal plane of Lu2CoMnO6 supercell. | ||
C Origin of the ferroelectricity and adiabatic path
The total electric polarization of the polar phase![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) tot can be represented as a summation of the electronic contribution
tot can be represented as a summation of the electronic contribution ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) ele and ionic contribution
ele and ionic contribution ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) ion, i.e.
ion, i.e. ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) tot =
tot = ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) ele +
ele + ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) ion. According to the description of King-Smith and Vanderbilt about the formalism of the Berry phase,26 the polarization contributed by the electrons is determined by examining the phase of the product of overlaps between cell-periodic Bloch functions along closely sampled strings of neighboring points in k-space. In the Lu2CoMnO6 system, the ↑↑↓↓ magnetic ordering leads the O sites to become nonequivalent, i.e. one between charge ordered Co and Mn ions with antiparallel spins (labeled as Oap) and the others between charge ordered Co and Mn ions with parallel spins (labeled as Op). Except for the spin order on the Co and Mn atom sites, the inequivalent sites of oxygen atoms are spin-polarized too (Op has ±0.02μB and Oap has ±0.03μB as induced magnetic moment). The inequivalences of Op and Oap were further determined by the spin density plot (Fig. 5(a)). Therefore, the spin order in the ↑↑↓↓ state causes the electronic contribution to the electronic polarization. The inequivalent oxygen atoms are also spin-polarized in the ↑↓↓↓, ↑↑↑↑ and ↑↓↑↓ magnetic states (Fig. 5(b)–(d)). However, the ↑↓↓↓, ↑↑↑↑ and ↑↓↑↓ spin orders do not break the spatial inversion symmetry.
ion. According to the description of King-Smith and Vanderbilt about the formalism of the Berry phase,26 the polarization contributed by the electrons is determined by examining the phase of the product of overlaps between cell-periodic Bloch functions along closely sampled strings of neighboring points in k-space. In the Lu2CoMnO6 system, the ↑↑↓↓ magnetic ordering leads the O sites to become nonequivalent, i.e. one between charge ordered Co and Mn ions with antiparallel spins (labeled as Oap) and the others between charge ordered Co and Mn ions with parallel spins (labeled as Op). Except for the spin order on the Co and Mn atom sites, the inequivalent sites of oxygen atoms are spin-polarized too (Op has ±0.02μB and Oap has ±0.03μB as induced magnetic moment). The inequivalences of Op and Oap were further determined by the spin density plot (Fig. 5(a)). Therefore, the spin order in the ↑↑↓↓ state causes the electronic contribution to the electronic polarization. The inequivalent oxygen atoms are also spin-polarized in the ↑↓↓↓, ↑↑↑↑ and ↑↓↑↓ magnetic states (Fig. 5(b)–(d)). However, the ↑↓↓↓, ↑↑↑↑ and ↑↓↑↓ spin orders do not break the spatial inversion symmetry.
The ionic contribution to the total electric polarization is simply described as
 | (8) |
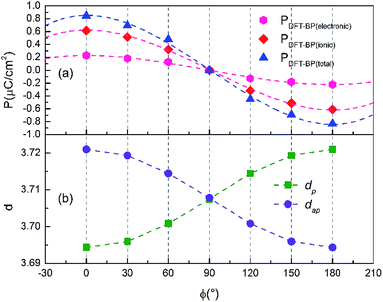
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) i, Ω, e and N atom represent the valence charge of the ith atom, the displacement of the ith atom, the unit-cell volume, the electron charge and the number of atoms in the unit cell, respectively. The geometrically optimized structure in the ↑↑↓↓ phase indicates that the off-centering displacements (Fig. 6) of Mn and Co (in-plane O) atoms can be 0.004 Å and 0.003 Å (0.002 Å) with respect to the initial P21/n symmetry. We also relaxed the structural parameters for the paraelectric ↑↓↑↓ (all neighboring spins antiparallel) and ↑↑↑↑ (all spins in the bc plane parallel) phases and compared them to experimental and the ↑↑↓↓ phase (Table 2), aiming to make a better comprehension of structural distortions induced by spin ordering. The values of angle αp and αap for ↑↑↑↑, ↑↓↓↓, and ↑↓↑↓ are larger than those from the experiments. Indeed, the off-centering displacements lead to an alternate long–short–short–long interlayer distance, with dp = 3.694 Å and dap = 3.721 Å, whereas dideal is 3.708 Å in the experimental CS case.9 For the ↑↑↓↓ phase, the calculations show a spontaneous polarization of 0.82 μC cm−2 along the b-axis and agree well with the experimental reports that found the polarization of single crystals is also along the b-axis,14 but are contrary to the polycrystalline results which suggest ferroelectricity along the c-axis.13 Different from the cases in DyFeO3 and HoMnO3,4,34 the direction of Pion is same as Pele and of the same order of magnitude, giving rise to a large polarization Ptot in Lu2CoMnO6. In perovskite DyFeO3,34 the direction of Pion is opposite to Pele and of the same order of magnitude, but Pion does not fully compensate for Pele. In addition, the exchange interaction, which induces magnetic ordering in perovskite DyFeO3 and HoMnO3, is the Fe3+–O2−–Fe3+ and Mn3+–O2−–Mn3+ super-exchange interaction, respectively. However, the exchange interaction is a Co2+–O2−–Mn4+ double-exchange mechanism in the double-perovskite Lu2CoMnO6.
i, Ω, e and N atom represent the valence charge of the ith atom, the displacement of the ith atom, the unit-cell volume, the electron charge and the number of atoms in the unit cell, respectively. The geometrically optimized structure in the ↑↑↓↓ phase indicates that the off-centering displacements (Fig. 6) of Mn and Co (in-plane O) atoms can be 0.004 Å and 0.003 Å (0.002 Å) with respect to the initial P21/n symmetry. We also relaxed the structural parameters for the paraelectric ↑↓↑↓ (all neighboring spins antiparallel) and ↑↑↑↑ (all spins in the bc plane parallel) phases and compared them to experimental and the ↑↑↓↓ phase (Table 2), aiming to make a better comprehension of structural distortions induced by spin ordering. The values of angle αp and αap for ↑↑↑↑, ↑↓↓↓, and ↑↓↑↓ are larger than those from the experiments. Indeed, the off-centering displacements lead to an alternate long–short–short–long interlayer distance, with dp = 3.694 Å and dap = 3.721 Å, whereas dideal is 3.708 Å in the experimental CS case.9 For the ↑↑↓↓ phase, the calculations show a spontaneous polarization of 0.82 μC cm−2 along the b-axis and agree well with the experimental reports that found the polarization of single crystals is also along the b-axis,14 but are contrary to the polycrystalline results which suggest ferroelectricity along the c-axis.13 Different from the cases in DyFeO3 and HoMnO3,4,34 the direction of Pion is same as Pele and of the same order of magnitude, giving rise to a large polarization Ptot in Lu2CoMnO6. In perovskite DyFeO3,34 the direction of Pion is opposite to Pele and of the same order of magnitude, but Pion does not fully compensate for Pele. In addition, the exchange interaction, which induces magnetic ordering in perovskite DyFeO3 and HoMnO3, is the Fe3+–O2−–Fe3+ and Mn3+–O2−–Mn3+ super-exchange interaction, respectively. However, the exchange interaction is a Co2+–O2−–Mn4+ double-exchange mechanism in the double-perovskite Lu2CoMnO6.
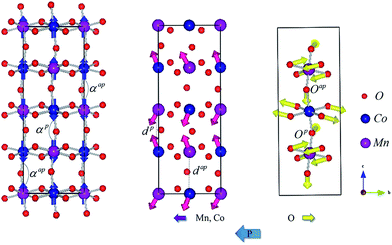 | ||
| Fig. 6 Left: the arrangement of Mn, Co and O ions in bc-plane. The directions of spin are represented as blue arrows. For middle and right plots, arrows denote the directions of the off-centering displacements for Co, Mn (middle) and O (right) in ↑↑↓↓ state. The direction of P is shown by thick arrows at the bottom. Structural parameters described in details in Table 2 are also marked in the left and middle pictures. | ||
The ↑↑↓↓ phase shows two scenarios E1 and E2 for the location of domain boundaries13 (as shown in the insets of Fig. 7(a)). The two distinct types of AFM domains were expected to show opposite electric polarizations −Ps and Ps. In the Lu2CoMnO6 supercell, the orientation of half of the spins in E1 are opposite to that in E2 (green highlighted regions in the central inset). Here, we consider a FE-AFM switching path from −Pc (E1) to Pc (E2) via a progressive rotation of the central spin orientations from 0° to 180°. The 90° spin configuration marked as ⊥ is depicted in the central inset in Fig. 7(a). Indeed, by fixing the ions at their centrosymmetric positions and turning spins from 0° to 180°, there is an energy change with respect to the FE phase, which increases from left to middle and decreases from middle to right. In this case, because the ions are fixed, the energy change is merely due to spin rotations and not due to the ionic off-centering displacement. As shown in Fig. 7(b), the electric polarization decreases from left to middle and increases from middle to right in the opposite direction, even when keeping the ions fixed in the CS structure. Then, by gradually rotating the spins, the electronic contribution to the total electric polarization is decreased. As a matter of fact, in the case of ions fixed at CS positions, for each spin configuration Pion = 0 and Ptot = Pele + Pion = Pele, the spin density connected with each spin configuration is gradually ‘non-polar’.
 | ||
| Fig. 7 (a) Total energy vs. the orientation of the central spins (blue marked regions in the insert plot denote the layers of spin rotation). (b) Ps calculated via DFT-BP for CSP. | ||
The FE state will be further stabilized by allowing the ionic positions to be relaxed. In other words, the symmetry lowered from the paraelectric (PE) to the FE phase and a concomitant decrease in the system's energy is induced by the spin rotation from perpendicular to parallel states. It is shown in Fig. 8(a) that Pion and Pele have the same direction and order of magnitude, giving rise to a total polarization Ptot of 0.82 μC cm−2 along the b-axis. We thus draw the following significant conclusion for Lu2CoMnO6: ↑↑↓↓ spin ordering induces symmetry breaking, which turns the system into a stable FE phase. Furthermore, the spin rotation not only leads to the charge redistribution, but also induces the changes in ionic off-centering displacements, as shown in Fig. 8(b), and the changes in interlayer distances measured along the polar axis (Fig. 8(b)). The mechanism for changes of interlayer dimerization driven by spin ordering is in accord with that reported in the literature.32,33 The abovementioned discussion shows a clear explanation of the complicated magnetic-field-suppressed polar states in the experimental data (Fig. 1 left and right of [13]).
We construct an adiabatic path by progressively rotating the Co/Mn spins from 90° to 0° along the ac-plane and from the PE to FE state. This adiabatic path is similar to that of DyFeO3,34 but is not unique. This rotation can be along the bc-plane, or other planes passing through the c-axis. We have explicitly drawn the available path for switching the polarization of one sublattice, as shown in Fig. ESI4.† On the other hand, Vilar et al.13 reported that in applied magnetic fields, the ↑↑ and ↓↓ domain walls slide apart due to their close proximity to a ferromagnetic instability. Thus, the regions of up spins become larger than those of down spins, which create a net magnetization. As the domain walls become less dense, the electric polarization is also suppressed. However, this expectation has not yet been confirmed due to the inherent average effects in the polycrystalline form with mixed orientations. The process of spin rotation between the antiferromagnetic ↑↑↓↓ state and metastable ferromagnetic ↑↑↑↑ state were simulated by our non-collinear magnetic calculations. We consider that the metastable ferromagnetic state will be the final state of antiferromagnetic spin-flopping, which is induced by applying strong magnetic fields. As discussed above, the ferrimagnetic ↑↑↑↓ state and ferromagnetic ↑↑↑↑ state do not allow a ferroelectric polarization to occur. Therefore, the electric polarization is suppressed gradually because of the spin-flop transitions35,36 induced by magnetic fields rather than metamagnetic transitions.
IV. Conclusions
The structure–property relationships of Lu2CoMnO6 were theoretically studied by first principles based on DFT. It is confirmed that the ground state magnetic ordering can be affected by the electronic Coulomb repulsion (Hubbard-U). For UCo = UMn = 3 eV, the calculations support a monoclinic P21 structure and ↑↑↓↓-type antiferromagnetic spin configuration, in which the structural parameters agree with the results from previous experiments. Our calculated results also show that the symmetry-driven inequivalence of the Co–O–Mn in-plane configurations with parallel and antiparallel spins can effectively induce ferroelectric polarization in the ↑↑↓↓-type Lu2CoMnO6. The spontaneous electric polarization is calculated to be 0.82 μC cm−2 along the b-axis. In addition to the exchange strictive mechanism, a more noticeable contribution from the electronic quantum effect of orbital polarization is found in the current study. Our theoretical investigations also predicted a magnetoelectric domain switching path, in which the 180° flop of ferroelectric polarization is induced by rotation of spins. Our calculations provide a fundamental understanding of the mechanism of ferroelectric polarization observed in Lu2CoMnO6.Acknowledgements
This work is supported financially by the National Natural Science Foundation of China (grant no.10904024), Program for Innovation Research of Science in Harbin Institute of Technology (PIRS of HIT A201413), Funded project of China Postdoctoral Science Foundation (grant no.20090460890), Project of Heilongjiang Postdoctoral Financial assistance (LBH-Z08158), Development Program for Outstanding Young Teachers in Harbin Institute of Technology (HIT) (HITQNJS. 2009. 071), and the Fundamental Research Founds for the Central Universities (HIT. NSRIF. 2012040). We thank the High Performance Computing Center of HIT for calculation resource.References
- W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442, 759 CrossRef CAS PubMed.
- D. V. Efremov, J. Van der Brink and D. I. Khomskii, Nat. Mater., 2004, 3, 853 CrossRef CAS PubMed.
- N. A. Spaldin and M. Fiebig, Science, 2005, 309, 391 CrossRef CAS PubMed.
- S. Picozzi, I. A. Sergienko, K. Yamauchi, B. Sanyal and E. Dagotto, Phys. Rev. Lett., 2007, 99, 227201 CrossRef CAS.
- J. K. Kim, S. S. Kim, W. J. Kim, A. S. Bhalla and R. Guo, Appl. Phys. Lett., 2006, 88, 132901 CrossRef PubMed.
- J. Van der Brink and D. I. Khomskii, J. Phys.: Condens. Matter, 2008, 20, 434217 CrossRef.
- A. B. Nicole and J. F. Craig, J. Phys. Chem. C, 2013, 117, 13339 Search PubMed.
- G. Sharma, J. Saha, S. D. Kaushik, V. Siruguri and S. Patnaik, Appl. Phys. Lett., 2013, 103, 012903 CrossRef PubMed.
- J. K. Murthy, K. D. Chandrasekhar, H. C. Wu, H. D. Yang, J. Y. Lin and A. Venimadhav, Europhys. Lett., 2014, 108, 27013 CrossRef.
- S. Kumar, G. Giovannetti, J. van den Brink and S. Picozzi, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134429 CrossRef.
- K. Kimura, H. Nakamura, S. Kimura, M. Hagiwara and O. Gunnarsson, Phys. Rev. Lett., 2009, 103, 107201 CrossRef CAS.
- B. B. Van Aken, T. T. M. Palstra, A. Filippetti and N. A. Spaldin, Nat. Mater., 2004, 3, 164 CrossRef CAS PubMed.
- S. Yáñez-Vilar, E. D. Mun, V. S. Zapf, B. G. Ueland, J. S. Gardner, J. D. Thompson, J. Singleton, M. Sánchez-Andújar, J. Mira and N. Biskup, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 134427 CrossRef.
- N. Lee, H. Y. Choi, J. Y. Jo, M. S. Seo, S. Y. Park and Y. J. Choi, Appl. Phys. Lett., 2014, 104, 112907 CrossRef PubMed.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689 CrossRef CAS.
- G. Kress and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef.
- G. Kress and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133 CrossRef.
- G. Giovannetti, S. Kumar, D. Khomskii, S. Picozzi and J. Van den Brink, Phys. Rev. Lett., 2009, 103, 156401 CrossRef.
- J. B. Neaton, C. Ederer, U. V. Waghmare, N. A. Spaldin and K. M. Rabe, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 014113 CrossRef.
- S. L. Dudarev, G. A. Botton, Y. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical Recipes: The Art of Scientific Computing, Cambridge University Press, New York, 1986 Search PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2008, 41, 653 CrossRef CAS.
- D. Dai and M. H. Whangbo, J. Chem. Phys., 2001, 114, 2887 CrossRef CAS PubMed.
- A. Savin, R. Nesper, S. Wengert and T. F. A. Fässler, Angew. Chem., Int. Ed. Engl., 1997, 36, 1808 CrossRef CAS PubMed.
- R. Amritendu, M. Somdutta, G. Rajeev, A. Sushil, P. Rajendra and G. Ashish, J. Phys.: Condens. Matter, 2011, 23, 325902 CrossRef PubMed.
- P. Ravindran, R. Vidya, A. Kjekshus and H. Fjellvåg, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 224412 CrossRef.
- Y. Tokunaga, S. Iguchi, T. Arima and Y. Tokura, Phys. Rev. Lett., 2008, 101, 097205 CrossRef CAS.
- Y. Tokunaga, N. Furukawa, H. Sakai, Y. Taguchi, T. Arima and T. Yoshinori, Nat. Mater., 2009, 8, 558 CrossRef CAS PubMed.
- A. Stroppa, M. Marsman, G. Kresse and S. Picozzi, New J. Phys., 2010, 12, 093026 CrossRef.
- E. Bousquet, N. A. Spaldin and K. T. Delaney, Phys. Rev. Lett., 2011, 106, 107202 CrossRef.
- I. Tsukada, J. Takeya, T. Masuda and K. Uchinokura, Phys. Rev. Lett., 2001, 87, 127203 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra03727a |
| This journal is © The Royal Society of Chemistry 2015 |