Investigation of the mechanical properties and local structural evolution of Ti60Zr10Ta15Si15 bulk metallic glass during tensile deformation: a molecular dynamics study†
Hui-Lung Chena,
Shin-Pon Ju*bc,
Tsang-Yu Wub,
Shih-Hao Liub and
Hsin-Tsung Chend
aDepartment of Chemistry and Institute of Applied Chemistry, Chinese Culture University, Taipei 111, Taiwan
bDepartment of Mechanical and Electro-Mechanical Engineering, National Sun Yat-sen University, Kaohsiung 804, Taiwan. E-mail: jushin-pon@mail.nsysu.edu.tw
cDepartment of Medicinal and Applied Chemistry, Kaohsiung Medical University, Kaohsiung 807, Taiwan
dDepartment of Chemistry, Chung Yuan Christian University, Chungli District, Taoyuan City 32023, Taiwan
First published on 17th June 2015
Abstract
Ti60Zr10Ta15Si15 bulk metallic glass (BMG) has been proven to have potential for use in orthopedic bone fixation devices, and further studies on its structural properties and deformation mechanism under uniaxial tension have been conducted using molecular dynamics (MD) simulations. The Honeycutt–Andersen (HA) index analysis, Voronoi tessellation method and Warren–Cowley short-range order parameter are employed to investigate its structural properties. The results show a high content of icosahedral-like structures, which suggests an amorphous state and a trend for silicon to pair with a metal atom. In its tensile test, the Ti60Zr10Ta15Si15 bulk metallic glass showed good ductility and an estimated Young's modulus of about 93 GPa, which is close to the experimental value. Local strain distribution was used to analyze the deformation mechanism, and the results show that shear bands develop homogeneously, which enhances the plasticity. The Voronoi tessellation analysis and HA index were used to further investigate the plastic/elastic deformation mechanism. The results of the HA analysis show that icosahedral local structures (1551, 1541, 1431) transfer to less dense structures (1422 and 1311), which shows an increase of open volume which can be attributed to the formation of the shear bands. In addition, the Voronoi tessellation analysis also shows a notable change from perfect icosahedra to distorted icosahedra. Further investigation shows the variations of the Voronoi index are mostly the Ti and Si-centered clusters. This suggests that the structures around Ti and Si atoms undergo a severe evolution during the tension process.
Introduction
Bulk metallic glasses (BMGs) have been proven to possess many material properties far superior to their crystalline counterparts, including higher tension and compression strength up to 6 GPa,1,2 larger elastic deformation strain limit up to 2%,3 and excellent corrosion resistivity.4 In recent years, much more attention has been paid to BMG's biomedical applications for artificial implants such as bone substitute applications or as orthopedic bone fixation devices.5–7 Previous studies have shown that Zr-based and Ti-based BMGs display high biocompatibilities with tests in NaCl and PBS (phosphate-buffered saline) solutions showing good corrosion resistance to chloride (Cl) and phosphorus (P) ions.5,8,9 Because of these two characteristics, BMGs have been commonly applied to materials for biodegradable implants for bone.10In 2007, Oak produced a series of biocompatible Ti-based BMGs without using toxic elements such as Ni and Cu.11 They have successfully prepared the fully amorphous ribbons in Ti–Zr–Ta–Si systems, and the results prove that these alloys possess high corrosion resistance in vivo and good ductility as measured by folding the specimen without observing any obvious cracks. Moreover, the Young's moduli of Ti–Zr–Ta–Si BMGs (∼88 GPa)11 are relatively close to that of human bone (∼30 GPa)12 when compared to 200 GPa and 106 GPa, respectively, for the 316 L stainless steel and Ti–6Al–4V alloy which are commonly used in the current biomedical industry.13 With Young's moduli closer to that of human bone, BMGs could prevent the occurrence of stress concentration at the interface between the BMG and the bone after the implant. Thus, the Ti–Zr–Ta–Si alloys have great potential for biomedical implants.
In the fabrication of biocompatible BMGs, the advantages of adding the Si element have been reported by several experimental studies. Wang et al. reported that small metalloid elements carbon (C), silicon (Si), and boron (B) may tighten the alloy structures and stabilize the amorphous alloy against crystallization.14 In Zhang's study, they stated that the benefits of additional Si would be the forming of efficiently packed local structures which are often associated with low energy and high viscosity of liquid.15 Hu's study also demonstrated that the dense and randomly packed clusters are the reason why smaller atoms can enhance the glass forming ability because these clusters make the redistribution of atoms on large range scale during the cooling process more difficult.16
Although the X-ray diffraction (XRD) profile can be used to evaluate the crystallinity of BMGs,17 it is very difficult to investigate the detailed local atomic arrangements around each compositional element and the variations of local atomic arrangements under external loading by the experimental approach directly. The possible alternative to investigate the local atomic arrangement of BMGs is by using numerical simulation. Among different numerical methods, molecular dynamics (MD) simulation can overcome the limitations of traditional empirical approaches and enable detailed observations on local structural variations and the deformation mechanism of BMGs under external loading on the atomic scale. For example, Wang studied the tensile behavior of a Cu46Zr46Al8 BMG at elevated temperatures by molecular dynamics simulation.18 The results show that open volume increases notably after pure elastic deformation, indicating that sufficient open volume activates the plastic deformation. Albe used MD to observe the shear band formation process for CuZr BMG and CuZr BMG with nanoglass.19 They found that plastic deformation is enhanced in the CuZr BMG with nanoglass due to the homogeneous shear band initiated around the BNG and nanoglass interfaces. In Zhang's study, the structure anisotropy is quantified through the information obtained by molecular dynamics.20 Results show that the major atomic pairs causing the structure's anisotropy are different in Cu50Zr50 and Cu64.5Zr35.5, and influence their deformation mechanisms.
From the discussions above, it is clear that MD simulation provides a powerful tool for investigating the variation of local atomic arrangements of Ti–Zr–Ta–Si BMG during the deformation process at the atomic level. Since Oak and Inoue have stated the optimal element composition of Ti–Zr–Ta–Si to avoid Cl and P corrosion is Ti60Zr10Ta15Si15, the BMG model with the same Ti, Zr, Ta, and Si compositions were used to explore the local atomic arrangements and deformation mechanism under tensile loading. To the best of our knowledge, this study is the first to provide the interaction parameters between Si and three other metal elements for this multi-element system by the force-matching method.21 By these potential parameters, the BMG model was constructed and the detailed local structural arrangements around each atom type were conducted.
Simulation model
In order to model the Ti–Zr–Ta–Si alloy system by molecular dynamics (MD) simulation, two potential functions, the tight-binding22 and Tersoff23 forms, were used to describe the interactions between different atomic pairs. The tight-binding potential is responsible for modeling the interaction between metallic element pairs and the Ta–Si pair, while the Si–Si, Zr–Si, and Ti–Si pairs are simulated by Tersoff potential.The tight-binding potential form is shown as eqn (1):
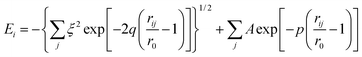 | (1) |
The Tersoff potential involving both two- and three-body terms is shown as eqn (2):
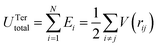 | (2) |
 | (3) |
fA = −Bij![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−uijrij) exp(−uijrij)
| (4) |
fR = Aij![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−λijrij) exp(−λijrij)
| (5) |
| bij = (1 + βiniζijni)−1/2ni | (6) |
 | (7) |
 | (8) |
 | (9) |
The coefficient bij corresponds to a many-body interaction and the function fc is merely a smooth cutoff function which limits the range of the potential. The function g(θijk) represents the influence of the bending angle.
The force-matching method (FMM)24 was used to determine all parameters of tight-binding and Tersoff potentials on the basis of binding energies and elastic constants of pure elements (Ti, Zr, Ta, Si) and binary metal systems including structures reported in experiment (Zr3Si2,25 ZrSi,26 ZrSi2,27 Ta2Si,28 Ta5Si3,28 TaSi2,29 TiSi,30 TiSi2,31 Ti3Si32) and those structures built by DFT calculation (ZrTi, TiTa, and ZrTa). These parameters can be seen in the ESI.†
After the parameters are fitted, they are used to generate the stable Ti60Zr10Ta15Si15 amorphous structure by the simulation anneal basin-hopping (SABH) method33 along the search direction for the energy local-minimal structure at higher energy. The unit cell with a total of 5000 atoms (3000 Ti, 500 Zr, 750 Ta and 750 Si atoms) is shown in Fig. 1(a), and the model shown in Fig. 1(b) for the tension test by MD was constructed by replicating the unit cell to 6 × 3 × 6 for the x, y and z axes.
Next, the MD simulation was performed by the large-scale atomic/molecular massively parallel simulator (LAMMPS) developed by Plimpton and co-workers.34 By MD simulation, the model was quenched from 1000 K to 300 K for 10 ps to relax the system with an NPT ensemble at 0 GPa. During the tensile process, the periodic boundary conditions (PBC) were applied to the x-, and y-dimensions and the open boundary was used in the z-dimension. The strain rates of 5 × 109, 1 × 109, 5 × 108, 4 × 108 and 2 × 108 m s−1 were examined for obtaining the appropriate strain rate for the current system. For 5 × 109 and 1 × 109 m s−1, the predicted strengths and the fracture strains are considerably lower than those from the MD simulations with the slower strain rates. By using the strain rates of 5 × 108, 4 × 108 and 2 × 108 m s−1, the strengths and the fracture strains are very close. For saving the simulation time, the strain rate of 5 × 108 m s−1 was used for the current study by increasing the z-dimensional length of the PBC box. During the tension process, the tensile stress at different strains was calculated by the following equation in LAMMPS code:35
 | (10) |
 is the effect of the pairwise potential function and indexes 1 and 2 indicate two atoms interacting with each other. The term
is the effect of the pairwise potential function and indexes 1 and 2 indicate two atoms interacting with each other. The term 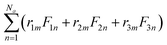 is the effect of bond angle to consider the three atoms involved in the interaction. Indexes of m and n represent the m plane and n-direction. The r is the interatomic distance between two atoms 1 and j, m is the weight of the atom, and Vi is a local volume defined by:
is the effect of bond angle to consider the three atoms involved in the interaction. Indexes of m and n represent the m plane and n-direction. The r is the interatomic distance between two atoms 1 and j, m is the weight of the atom, and Vi is a local volume defined by:
 | (11) |
Results and discussion
The Ti60Zr10Ta15Si15 unit cell of 5000 atoms obtained by SABH method was characterized by the X-ray diffraction (XRD) module REFLEX36–38 in Accelrys Materials Studio 5.5.39 In REFLEX, Bragg's law is used to obtain the constructive interference intensity for X-rays scattered by materials, and its formula is listed as follows:
 | (12) |
The XRD and RDF profiles of Ti60Zr10Ta15Si15 are shown in Fig. 2(a) and (b). One can see no specific crystalline peak appearing in the 2θ range between 10–90° for the XRD profile, and the range of the XRD peak is located between 35–43°, which is consistent with the previous experimental XRD profile of Ti60Zr10Ta15Si15.40 For the RDF profile, the broad splitting second peak indicates the amorphous configuration of Ti60Zr10Ta15Si15, which is consistent with the inference of the short range order by the XRD profile. According to the XRD and RDF profiles shown in Fig. 2(a) and (b), the Ti60Zr10Ta15Si15 structure constructed by SABH is amorphous and corresponds to realistic Ti60Zr10Ta15Si15 BMG in experiment.
A further study into the local microstructural distribution for Ti60Zr10Ta15Si15 BMG was conducted by using the Honeycutt–Anderson (HA) pair analysis.40 The detailed definition of the HA index can be found elsewhere41,42 and is not presented here. The HA indexes of 1421 and 1422 represent f.c.c. and h.c.p. crystal structures, and 1431, 1541, and 1551—which occupy the largest fraction in the amorphous or liquid state—are used to search the icosahedral local structures. The 1551 pair is particularly characteristic of the icosahedral ordering; the 1541 and 1431 are indexes for the defect icosahedra and f.c.c. defect local (or distorted icosahedra) structures, respectively. HA indexes 1661 and 1441 are employed to identify the local b.c.c. structure. Finally, the indexes 1321 and 1311 are the packing related to rhombohedral pairs which tend to evolve when the 1551 packing forms, which can be viewed as the side product accompanying icosahedral atomic packing. The schematic diagrams for the HA indexes introduced above can be clearly seen in Fig. 3(a).
 | ||
| Fig. 3 (a) Schematic diagrams corresponding to several characteristic HA indexes; (b) HA index numbers for Ti60Zr10Ta15Si15 BMG. | ||
Fig. 3(b) shows the HA index distribution of Ti60Zr10Ta15Si15 BMG, and the fraction of icosahedra-like local structures (1551, 1541, and 1431) are over 70%. The fractions of these three icosahedra-like structures are very close and each of them occupies about 23% of all HA fractions. For other HA indexes, the b.c.c local structures (1441 and 1661), h.c.p local structure (1422), rhombohedral local structures (1321 and 1311), and f.c.c. local structure (1421) are about 7.5, 9.1, 7.2, and 6.7%, respectively. The high HA fractions of icosahedra-like structures verify the amorphous Ti60Zr10Ta15Si15 structure and are consistent with the HA analysis results reported previously for BMGs.
Since the atomic radii of Zr, Ti, Ta, and Si are 1.55, 1.47, 1.46, and 1.11 Å, with the atomic size of Si smaller than the other three by about 24.0–28.4%, the HA fraction distribution for different atom type pairs could be very different. Because the HA index profiles shown in Fig. 3(b) do not contain enough information about the HA fraction distributions for different atom pairs, they should be analyzed to better understand the local structural arrangements around different atom pairs with different pair lengths. The HA indexes of different the atomic pairs in Ti60Zr10Ta15Si15 BMG are shown in Fig. 4. Because Ti occupies the highest atomic fraction of Ti60Zr10Ta15Si15 BMG, the Ti-related HA indexes (Zr–Ti, Ti–Ti, Ti–Ta, and Ti–Si) are relatively higher than those for other atom type pairs. The summations of the icosahedra-like HA indexes 1551, 1541, and 1431, referring to the liquid local structures, are about 23.02, 13.14, 7.81 and 8.06% for the atom pairs of Ti–Ti, Ti–Ta, Ti–Si and Ti–Zr, respectively.
HA index analysis can provide detailed fraction distribution of different local structural configurations around all two bonded-atom pairs of the system. However, the HA index lacks the information to describe the complete morphology surrounding an investigated atom. Thus, further classification of the polyhedral order is performed by using the Voronoi tessellation analysis.43,44 The Voronoi polyhedra (VP) are constructed from all edges formed by the intersections of the planes halfway between the central atom and all of its first neighbor atoms. The Voronoi indexes (n3, n4, n5, n6) are classified based on the number of edges making up each polyhedral face. These indexes, n3, n4, n5, and n6, are the numbers of 3-, 4-, 5-, and 6-edged faces comprising the polyhedron. Consequently, the summation of n3, n4, n5, and n6 is the coordination number of the referenced atom. For example, the Voronoi indexes of the perfect ICO, BCC, and FCC/HCP are (0,0,12,0), (0,6,0,8) and (0,12,0,0), respectively. However, the VPs will be distorted to many other VP forms when compared to their crystalline counterparts because of the thermal noise or atoms in the amorphous system. Therefore, only the most frequently observed VPs from previous studies43–47 are discussed. These VPs include (0,2,8,1), (1,0,9,3), (0,1,10,2), (0,3,6,2), (0,4,4,3), (0,3,6,3), (0,2,8,2), and (0,4,4,4) for deformed icosahedrons; (0,3,6,5), (0,4,4,6), and (0,4,4,7) for deformed f.c.c.; and (0,2,8,4) for deformed b.c.c. These results are shown in Fig. 5, and the higher (0,0,12,0) fraction for Si indicates that the ideal icosahedral structures are prone to construct around Si atoms, while the distorted icosahedral structures are mainly constructed around Ti and Si atoms. This VP analysis result indicates that the Si atom, having the smallest radius, enhances the formation of local icosahedral or deformed icosahedral clusters and therefore improves the glass forming ability by forming more dense and more viscous local Si icosahedra-like clusters.
 | ||
| Fig. 5 The Voronoi index and the center atom composition for different pairs in the Ti60Zr10Ta15Si15 BMG. | ||
Table 1 lists the average coordination numbers (CNs) of Ti, Zr, Ta, and Si atoms in Ti60Zr10Ta15Si15 BMG as well as the partial coordination numbers of different atomic pairs. The coordinate number was calculated by counting the amount of first neighbor atoms around the center atom. The first subscript for atomic pair indicates the type of the reference atom and the second subscript stands for the atom type of the first neighbor of the reference atom. Among the average CNs of these four elements, the Zr and Si atoms have the highest and lowest CNs of 13.63 and 11.04, respectively. Since in the Ti60Zr10Ta15Si15 BMG, the atomic size of Zr is the largest and Si is smallest, this suggests that the atom with the larger atomic size tends to be located at the center of a cluster with a higher CN. A closer investigation of the partial CNs of Zr–Si, Ti–Si, Ta–Si, and Si–Si shows that the partial CN of Zr–Si is the highest and that of Si–Si is the lowest. Thus, the larger atom provides more open volume for the placement of the first neighbor atom of a smaller size.
| Ti60Zr10Ta15Si15 BMGs | |||||
|---|---|---|---|---|---|
| Type | Zr–Zr | Zr–Ti | Zr–Ta | Zr–Si | Zr_Total |
| Nij | 1.13 ± 1.09 | 8.11 ± 1.97 | 2.11 ± 1.28 | 2.28 ± 1.24 | 13.63 ± 1.65 |
| Type | Ti–Zr | Ti–Ti | Ti–Ta | Ti–Si | Ti_Total |
| Nij | 1.39 ± 1.11 | 7.31 ± 1.85 | 2.12 ± 1.11 | 1.73 ± 1.15 | 12.55 ± 1.51 |
| Type | Ta–Zr | Ta–Ti | Ta–Ta | Ta–Si | Ta_Total |
| Nij | 1.40 ± 1.06 | 8.11 ± 1.94 | 1.51 ± 1.09 | 1.83 ± 1.07 | 12.84 ± 1.57 |
| Type | Si–Zr | Si–Ti | Si–Ta | Si–Si | Si_Total |
| Nij | 1.44 ± 1.14 | 7.05 ± 1.70 | 1.87 ± 0.90 | 0.69 ± 0.83 | 11.04 ± 1.76 |
The Warren–Cowley chemical short-range-order (CSRO) analysis48 for Ti60Zr10Ta15Si15 BMG was employed to quantify the attraction and repulsion between element pairs. With the CN information shown in Table 1, the chemical affinities of a referenced atom with its first neighbor atoms are evaluated by the CSRO parameter. The definition of this parameter is as the following equation:
 | (13) |
The CSRO parameters of all pairs of Ti60Zr10Ta15Si15 BMG are listed in Table 2. The results show that the CSRO parameters for Zr–Zr, Ta–Ta, and Si–Si are positive and that of Ti–Ti is relatively close to zero. This CSRO analysis result indicates the Ti atom has no preference to another Ti atom, and the three other elements display less affinity to themselves, indicating that this alloy easily forms the glassy structure and has higher thermal stability. Furthermore, most CSRO parameters of Si-related pairs are negative except for Ti–Si, and Ta–Si pairs with smaller CSRO values, indicating that the affinities between Si and the three other metal elements are relatively higher than Zr–Zr, Ta–Ta, and Ti–Ti. The Si–Si and Si–Zr CSRO values are the most positive and the negative among all atom pairs, and this reveals that the smallest atom, Si, tends to pair with a metal atom instead of itself. Because the Zr is the largest atom of Ti60Zr10Ta15Si15 BMG, Si has the highest affinity to the Zr atom. With these results, one can realize that a diversity of atom sizes in the solution can advance the formation of the amorphous state. When this increases, it is relatively easy to form the amorphous structure because the higher fractions of denser icosahedra-like local structures decrease the atomic mobility and lead to a more viscous solution.
| Ti60Zr10Ta15Si15 BMG | ||||
|---|---|---|---|---|
| Type | Zr–Zr | Zr–Ti | Zr–Ta | Zr–Si |
| αij | 0.171 | 0.008 | −0.032 | −0.115 |
| Type | Ti–Zr | Ti–Ti | Ti–Ta | Ti–Si |
| αij | −0.108 | 0.029 | −0.126 | 0.081 |
| Type | Ta–Zr | Ta–Ti | Ta–Ta | Ta–Si |
| αij | −0.090 | −0.053 | 0.216 | 0.050 |
| Type | Si–Zr | Si–Ti | Si–Ta | Si–Si |
| αij | −0.304 | −0.064 | −0.129 | 0.583 |
Fig. 6 shows the stress–strain profile and ΔV/V value with strain for the Ti60Zr10Ta15Si15 BMG under tension. One can see the stress increases linearly with strain while strain increases from 0 to 0.05, indicating the elastic behavior of Ti60Zr10Ta15Si15 BMG is located within this strain range. The Young's modulus derived from the slope of the stress–strain profile at the elastic region is about 93 GPa, while the corresponding experimental value is about 88 GPa.11 The predicted Young's modulus is slightly larger than the experimental value by about 5.7%, indicating our simulation model by the TB and Tersoff potentials can realistically reflect the mechanical properties of Ti60Zr10Ta15Si15 BMG. At strains from 0.05 to 0.33, the stress displays a parabolic increase with the increasing strain, and reaches its maximal value about 12.25 GPa. At strains from 0.33 to 0.36, the stress shows an abrupt drop from its maximal value, indicating the occurrence of fracture.
The ΔV/V value, the ratio of open volume (ΔV) to the system volume at strain 0 (V), was used to indicate the volume variation during the tension process. It is a general view that more open volume allows for more plastic deformation.18 The system volume is defined as the summation of the atomic volume calculated by eqn (14), and the ΔV value is calculated by the following equation:
| ΔV = Vε − V0 | (14) |
The atomic local shear strain ηMisesi of an individual atom, introduced by Shimizu et al.,49 was used to monitor the development of shear transition zones (STZ) and the formation of the shear band within Ti60Zr10Ta15Si15. The detailed definition of ηMisesi can be found in ref. 50 of this study and is therefore not introduced here. A large ηMisesi value indicates atom i is under local plastic and shear deformation, whereas a small ηMisesi value implies atom i undergoes a small amount of movement relative to all its first neighbor atoms or atom i is under local elastic deformation.
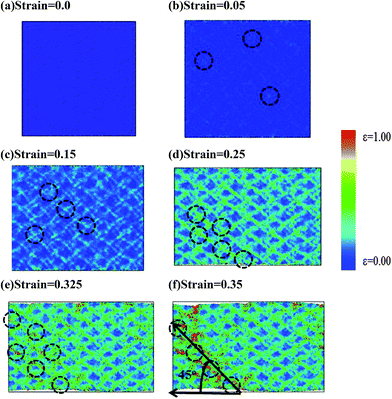
Fig. 7(a)–(f) shows snapshots of Ti60Zr10Ta15Si15 BMG with atomic ηMisesi values at strains of 0, 0.05, 0.15, 0.25, 0.325 and 0.35, which are labelled as the letters a–f on the stress–strain curve of Fig. 6. For the reference structure at strain of 0, the ηMisesi value of each atom is 0, and the initialization of STZs labeled by dashed circles in Fig. 7(b) occurs at strain of 0.05. These STZs distribute randomly within Ti60Zr10Ta15Si15 BMG. From Fig. 6, one can infer that the sufficient open volume increase significantly activates the initialization of shear banding and enhances the appearance of STZs when the strain exceeds the yielding strain. At strain of 0.15, the extension of STZs begins to form several shear bands, as shown in Fig. 7(c), and more shear bands can be seen in Fig. 7(d) for Ti60Zr10Ta15Si15 BMG at strain of 0.25. In Fig. 6, the ΔV/V value increases more significantly with the strain when the strain exceeds 0.15. From the ηMisesi distributions shown in Fig. 7(c) and (d), one can note that the increase in the shear band number results in the significant increase of the open volume and a local structure rearrangement. The shear bands propagate at a direction 45° from the tensile direction and intersect with one another, resulting in the vein-like pattern. This vein-like pattern can be also seen in previous theoretical51 and experimental studies.11,52 These results show that good ductility of Ti60Zr10Ta15Si15 might be caused by the homogeneous development of shear bands which increase the deformed area. Fig. 7(e) and (f) show the fracture areas at strains of 0.325 and 0.35, where considerable atomic rearrangements occur.
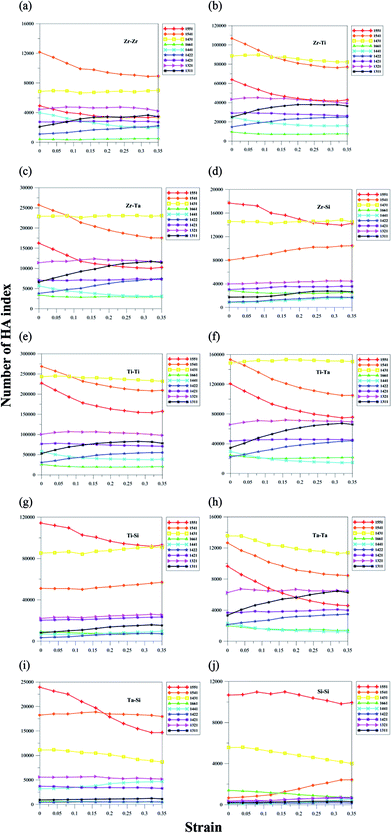
To understand the local structural rearrangement during the tension process, the numbers of different HA pairs for Ti60Zr10Ta15Si15 BMG at different strains during the tension are illustrated in Fig. 8. The vertical axis represents the total number of one particular HA pair and the horizontal axis is the tensile strain. The reason that this study uses the number of pairs instead of pair fraction is that total bonding pairs at each strain will decrease due to increasing distance between atoms during the tensile process such that the fraction is not the best choice to represent the variation of local structure. It can be seen from Fig. 8 that at different strains, the icosahedral local structures 1431, 1541, and 1551 are predominant. Among all HA pairs, there are four indexes with notable changes. The 1551 and 1541 HA indexes referring to the icosahedral and defected icosahedral structures show considerable decreases such that the pair numbers of 757![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 007 and 732
007 and 732![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 142 for 1551 and 1541 at the beginning of the tensile test become 548
142 for 1551 and 1541 at the beginning of the tensile test become 548![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 and 601
512 and 601![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 358 at strain of 0.35. For 1422 and 1311, these two HA indexes increase with the strain from 85
358 at strain of 0.35. For 1422 and 1311, these two HA indexes increase with the strain from 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 203 and 146
203 and 146![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 013 to 156
013 to 156![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 471 and 240
471 and 240![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939, respectively. Since the second index of the HA analysis is the number of common neighbor atoms between the investigated atomic pair, the decrease of HA indexes with the larger second indexes implies the local structures in Ti60Zr10Ta15Si15 BMG become less dense during the tensile process.
939, respectively. Since the second index of the HA analysis is the number of common neighbor atoms between the investigated atomic pair, the decrease of HA indexes with the larger second indexes implies the local structures in Ti60Zr10Ta15Si15 BMG become less dense during the tensile process.
Because the atomic radii of Zr, Ti, Ta and Si are different, the variations of HA index numbers for different atom type pairs during the tension process could be very different. Fig. 9(a)–(j) shows the HA index numbers for different atom pairs of Ti60Zr10Ta15Si15 BMG at different strains during the tension process. The HA indexes of different atom pairs show two distribution patterns of the icosahedra-like structures. For Si-related HA atom pairs (Zr–Si, Ti–Si, Ta–Si, and Si–Si) at strain of 0, the icosahedral structures (1551) are the most populous among all indexes in Fig. 9(d), (g), (i) and (j). For other atom pairs, the defected icosahedra (1541) or distorted icosahedra (1431) structures have higher numbers than other HA indexes.
Although the 1431 HA fraction of all atom pairs remains constant during the tension process shown in Fig. 8, the 1431 HA fraction of the Ti–Si pair displays an increasing trend when the strain is larger than 0.15, whereas the 1431 fractions of Ta–Ta, Ta–Si, and Si–Si pairs decrease with the increasing strain. For other atom pairs in Fig. 9(a)–(f), the 1431 numbers remain almost the same at different strains. For the 1551 HA index, the numbers of all atom pairs decrease with increasing strain. For Si-related atom pairs, the 1551 numbers display a more significant decrease when strain is larger than the yielding strain of 0.05. For the Si–Si pair, the 1551 number remains almost constant until the strain of 0.15, at which the shear band begins to form and the shear band number increases. For the defected icosahedra HA index 1541, Ti–Si, Zr–Si, and Si–Si increase with the strain, even though the 1541 number of all atom pairs in Fig. 8 displays a significant decrease with the increasing strain. It should be noted that the HA index distribution of the Si–Si pair is very different from those of other atom pairs. The fraction of the defected icosahedra HA index (1541) is relatively much lower than those of other atom pairs, and the (1551) icosahedra HA fraction is much higher than those of other atom pairs. As the strain exceeds 0.15, the increase in the 1541 number of the Si–Si pair can be attributed to the decrease of 1551 and 1431 numbers.
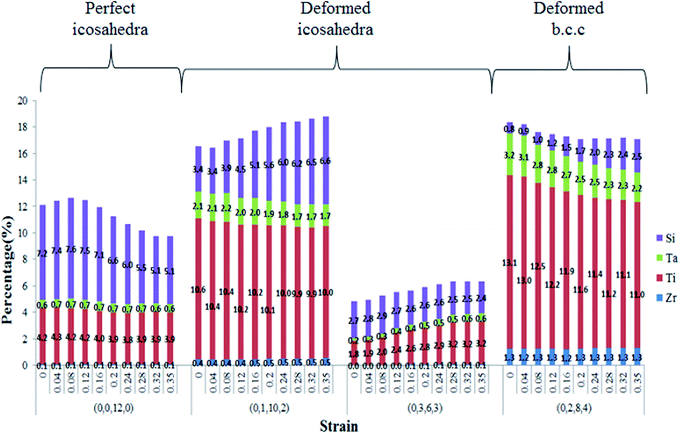
The variations of local cluster structures during the tension were investigated by the Voronoi tessellation analysis. Fig. 10 shows the Voronoi index variations during the tensile process. At strain between 0 and 0.05, the fractions of all VP indexes display only slight variation, indicating that most cluster structures do not rearrange at strain within the elastic region. When the strain exceeds 0.05, however, the deformed icosahedra fractions of (0,1,10,2), (0,3,6,3), and (0,4,4,4) increase considerably with strain, whereas the fraction of the distorted b.c.c. (0,2,8,4) decreases. It should be noted that the icosahedra (0,0,12,0) VP fraction slightly increases when the strain increases from 0.05 to 0.08 and then undergoes a significant decrease when the strain is larger than 0.15. From these results and the ηMisesi distributions shown in Fig. 7(b)–(d) for strains of 0.05, 0.15, and 0.25, it can be inferred that once the strain exceeds the yielding strain of 0.05, the deformed icosahedral clusters appear within the STZs, and the shear bands formed by the evolution of STZs at strain of 0.15 increase and result in the decrease of icosahedral clusters and the increase of open volume shown in Fig. 6.
Because the VP fractions of (0,0,12,0), (0,1,10,2), (0,3,6,3), and (0,2,8,4) indexes have significant changes during the tension process, the fractions of these four VP indexes with different center atoms are given in Fig. 11. It is apparent that the fraction of icosahedral clusters with the Si center atom significantly decreases and transforms into a deformed icosahedral and b.c.c. clusters.
 | ||
| Fig. 11 Notable changes in center atoms for four Voronoi indexes at different strain for Ti60Zr10Ta15Si15 BMG. | ||
As shown in the discussion above, icosahedral clusters play a crucial role in the tension process. Previous studies53,54 have reported that the perfect icosahedra, which refers to 1551 HA index and (0,0,12,0) in Voronoi tessellation analysis, has high corrosion resistivity and high density. Moreover, the work of Cao et al.55 has suggested that the onset of local instability will be triggered by structural softening. Thus, it is proposed that the STZs tend to be initiated at the regions with higher fractions of icosahedral local structures for different atom type pairs, and icosahedral structures become more disordered and more loosely packed clusters due to tensile loading. These instabilities then nucleate and lead to the formation of STZs. With increasing strain, STZs extend along a direction 45° from the tensile direction to form multiple shear bands, as shown in Fig. 7, and finally cause the fracture.
Conclusion
Molecular dynamics simulation has been conducted to investigate the structural and mechanical properties of Ti60Zr10Ta15Si15 BMG. The unit cell of Ti60Zr10Ta15Si15 BMG built by the SABH method is examined by XRD and no specific crystalline peak is found, indicating these two BMGs from our SABH prediction are totally amorphous. From HA index and Voronoi index analyses, the icosahedra-like structures that indicate liquid local structures appear to be the major local structures in the Ti60Zr10Ta15Si15 BMG, with these icosahedra-like structures prone to form around Ti and Si atoms. The considerable icosahedra-like structures improve the glass forming ability by forming denser and more stable local clusters. Furthermore, chemical affinities are investigated by CSRO parameters. The CSRO parameter of the Zr–Si pair has the most positive value, which indicates that the smaller Si atom tends to pair with a metal atom instead of itself and therefore demonstrates the fact that a high diversity of atom sizes in the solution will advance the formation of the amorphous state.Based on the stress–strain profile obtained from the tensile test, the predicted Young's modulus is close to the available experimental results, indicating that the current simulation model using the TB and Tersoff potentials can accurately reflect the realistic atomic interaction among Ti, Zr, Ta and Si atoms. Besides the Honeycutt–Anderson (HA) pair analysis and Voronoi tessellation analysis, analysis of variation in the open volume is also employed to monitor the development of STZ56 and the evolution of the shear band. The distributions of the stress–strain curve and open volume with strain show linear increases of stress–strain and open volume–strain curves which suggest an elastic region. Moreover, stress and open volume increase significantly at STZ initialization stages. This can be attributed to an increase in the number of shear bands, resulting in a significant increase of open volume and the activation of local structure rearrangement. In addition, shear bands measured by the local atomic strain develop along a direction 45° from the tensile direction and indicate good ductility of the Ti60Zr10Ta15Si15 BMG. This ductility is due to the homogeneous development of shear bands that cause a larger area to undergo plastic deformation.
As shown by the HA index analysis during the tensile test, Si-related pairs have a relatively higher content of perfect icosahedral local structures (1551), while other pairs are dominated by defect (1541) and distorted (1431) icosahedra. Less dense indexes (1422 and 1311) are found to increase for all pairs with increasing strain, consistent with the results of a parabolic increase of open volume with increasing strain. Further, Voronoi tessellation analysis shows that (0,0,12,0), (0,1,10,2), (0,3,6,3) and (0,2,8,4) forms undergo the most notable changes during the tensile process. With strain increase, local structures surrounding Si transform from perfect icosahedra (0,0,12,0) to distorted icosahedra (0,1,10,2) and (0,3,6,3), while local structures surrounding Ti transform from (0,2,8,4) b.c.c.-like structures in liquid state to distorted icosahedral ones (0,3,6,3). The HA and Voronoi index results show the change from denser local structures to loose local structures that lead to the increase in open volume. Furthermore, these loose and unstable clusters will gather to form the shear band and the fracture occurs after the extension of STZs.
References
- J. Wang, R. Li, N. Hua and T. Zhang, Co-based ternary bulk metallic glasses with ultrahigh strength and plasticity, J. Mater. Res., 2011, 26, 2072 CrossRef CAS.
- Z. Q. Liu and Z. F. Zhang, Strengthening and toughening metallic glasses: The elastic perspectives and opportunities, J. Appl. Phys., 2014, 115, 163505 CrossRef PubMed.
- W. L. Johnson, MRS Bull., 1999, 24, 42–56 CrossRef CAS.
- A. Inoue, Acta Mater., 2000, 48, 279–306 CrossRef CAS.
- J. J. Oak, D. V. Louzguine-Luzgin and A. Inoue, Fabrication of Ni-free Ti-based bulk-metallic glassy alloy having potential for application as biomaterial, and investigation of its mechanical properties, corrosion, and crystallization behavior, J. Mater. Res., 2007, 22, 1346–1353 CrossRef CAS.
- J. F. Wang, Y. Y. Wei, S. F. Guo, S. Huang, X. E. Zhou and F. S. Pan, The Y-doped MgZnCa alloys with ultrahigh specific strength and good corrosion resistance in simulated body fluid, Mater. Lett., 2012, 81, 112–114 CrossRef CAS PubMed.
- S. Zhu, G. Xie, F. Qin, X. Wang and A. Inoue, Ni- and Be-free Zr-based bulk metallic glasses with high glass-forming ability and unusual plasticity, J. Mech. Behav. Biomed. Mater., 2012, 13, 166–173 CrossRef CAS PubMed.
- H. F. Li, Y. F. Zheng, F. Xu and J. Z. Jiang, In vitro investigation of novel Ni free Zr-based bulk metallic glasses as potential biomaterials, Mater. Lett., 2012, 75, 74–76 CrossRef CAS PubMed.
- X. N. Gu, N. Li, Y. F. Zheng and L. Q. Ruan, In vitro degradation performance and biological response of a Mg-Zn-Zr alloy, Mater. Sci. Eng., B, 2011, 176, 1778–1784 CrossRef CAS PubMed.
- B. Zberg, P. J. Uggowitzer and J. F. Loffler, MgZnCa glasses without clinically observable hydrogen evolution for biodegradable implants, Nat. Mater., 2009, 8, 887–891 CrossRef CAS PubMed.
- J.-J. Oak and A. Inoue, Attempt to develop Ti-based amorphous alloys for biomaterials, Mater. Sci. Eng., A, 2007, 449, 220–224 CrossRef PubMed.
- J.-Y. Rho, T. Y. Tsui and G. M. Pharr, Elastic properties of human cortical and trabecular lamellar bone measured by nanoindentation, Biomaterials, 1997, 18, 1325–1330 CrossRef CAS.
- S. F. Guo, Z. Liu, K. C. Chan, W. Chen, H. J. Zhang, J. F. Wang and P. Yu, A plastic Ni-free Zr-based bulk metallic glass with high specific strength and good corrosion properties in simulated body fluid, Mater. Lett., 2012, 84, 81–84 CrossRef CAS PubMed.
- W. H. Wang, P. W. Z. Bian, Y. Zhang, M. X. Pan and D. Q. Zhao, Role of addition in formation and properties of Zr-based bulk metallic glasses, Intermetallics, 2002, 10, 1249–1257 CrossRef CAS.
- B. Zhang, Y. Jia, S. Wang, G. Li, S. Shan, Z. Zhan, R. Liu and W. Wang, Effect of silicon addition on the glass-forming ability of a Zr–Cu-based alloy, J. Alloys Compd., 2009, 468, 187–190 CrossRef CAS PubMed.
- Y. Hu, M. X. Pan, L. Liu, Y. H. Zhao, D. Q. Zhao and W. H. Wang, Synthesis of Fe-based bulk metallic glasses with low purity materials by multi-metalloids addition, Mater. Lett., 2003, 57, 2698–2701 CrossRef CAS.
- G. Duan, D. Xu, Q. Zhang, G. Zhang, T. Cagin, W. L. Johnson and W. A. Goddard, Molecular dynamics study of the binary metallic glass motivated by experiments: Glass formation and atomic-level structure, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 224208 CrossRef.
- X. D. Wang, H. B. Lou, J. Bednarcik, H. Franz, H. W. Sheng, Q. P. Cao and J. Z. Jiang, Structural evolution in bulk metallic glass under high-temperature tension, Appl. Phys. Lett., 2013, 102, 051909 CrossRef PubMed.
- D. Sopu, Y. Ritter, H. Gleiter and K. Albe, Deformation behavior of bulk and nanostructured metallic glasses studied via molecular dynamics simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 100202 CrossRef.
- Y. Zhang, N. Mattern and J. Eckert, Molecular dynamic simulation study of the structural anisotropy in Cu50Zr50 and Cu64.5Zr35.5 metallic glasses induced by static uniaxial loading within the elastic regime, J. Alloys Compd., 2011, 509(suppl. 1), S74–S77 CrossRef CAS PubMed.
- G. Grochola, S. P. Russo and I. K. Snook, On fitting a gold embedded atom method potential using the force matching method, J. Chem. Phys., 2005, 123, 204719 CrossRef PubMed.
- F. Cleri and V. Rosato, Tight-Binding Potentials for Transition-Metals and Alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 22–33 CrossRef CAS.
- J. Tersoff, Modeling Solid-State Chemistry - Interatomic Potentials for Multicomponent Systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 5566–5568 CrossRef.
- F. Ercolessi and J. B. Adams, Interatomic Potentials from 1st-Principles Calculations - the Force-Matching Method, Europhys. Lett., 1994, 26, 583–588 CrossRef CAS.
- O. Schob, F. Benesovsky and H. Nowotny, Strukturbestimmung an Einigen Phasen in Den Systemen - Zr-Al-Si Und Hf-Al-Si[Zral3(Si) - Zrsi(Al), Hf(Si,Al) - Zr3si2-Hf3si2], Monatsh. Chem., 1961, 92, 1218–1226 CrossRef.
- A. Raman and K. Schubert, Z. Metallkd., 1965, 56, 44–52 CAS.
- M. Setton and J. Vanderspiegel, Structural and electrical-properties of ZRSI2 and ZR2CUSI4 formed by rapid thermal-processing, J. Appl. Phys., 1991, 70, 193–197 CrossRef CAS PubMed.
- O. G. K. Y. A. Kocherzhinskii and E. A. Shishkin, Dokl. Chem., 1981, 261, 464–465 Search PubMed.
- I. Engström and B. Lönnberg, Thermal expansion studies of the group IV–VII transition–metal disilicides, J. Appl. Phys., 1988, 63, 4476–4484 CrossRef PubMed.
- N. F. P. G. V. Samsonov and L. A. Dvorina, Inorg. Mater., 1977, 13, 1429–1431 Search PubMed.
- J. Jongste, O. Loopstra, G. Janssen and S. Radelaar, Elastic constants and thermal expansion coefficient of metastable C49TiSi2, J. Appl. Phys., 1993, 73, 2816–2820 CrossRef CAS PubMed.
- Y. A. K. V. N. Svechnikov, L. M. Yupko, O. G. Kulik and E. A. Shishkin, Dokl. Chem. Technol., 1970, 192, 82–85 Search PubMed.
- D. J. Wales and J. P. K. Doye, Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms, J. Phys. Chem. A, 1997, 101, 5111–5116 CrossRef CAS.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- N. Miyazaki and Y. Shiozaki, Calculation of mechanical properties of solids using molecular dynamics method, JSME Int. J., Ser. A, 1996, 39, 606–612 Search PubMed.
- G. S. Pawley, Unit-Cell Refinement from Powder Diffraction Scans, J. Appl. Crystallogr., 1981, 14, 357–361 CrossRef CAS.
- H. M. Rietveld, A Profile Refinement Method for Nuclear and Magnetic Structures, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- J. E. Post and D. L. Bish, Rietveld Refinement of Crystal-Structures Using Powder X-Ray-Diffraction Data, Rev. Mineral., 1989, 20, 277–308 Search PubMed.
- I. Accelrys Software, Materials Studio, Release 5.5, ed. Accelrys Software, Inc., San Diego, CA, 2009 Search PubMed.
- X. Q. Wu, H. L. Wang and J. G. Lin, Effects of Sn content on thermal stability and mechanical properties of the Ti60Zr10Ta15Si15 amorphous alloy for biomedical use, Mater. Des., 2014, 63, 345–348 CrossRef CAS PubMed.
- J. D. Honeycutt and H. C. Andersen, Molecular-Dynamics Study of Melting and Freezing of Small Lennard-Jones Clusters, J. Phys. Chem., 1987, 91, 4950–4963 CrossRef CAS.
- Y. C. Lo, J. C. Huang, S. P. Ju and X. H. Du, Atomic structure evolution of Zr-Ni during severe deformation by HA pair analysis, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 024103 CrossRef.
- T. Debela, X. Wang, Q. Cao, D. Zhang, S. Wang, C. Wang and J. Jiang, Atomic structure evolution during solidification of liquid niobium from ab initio molecular dynamics simulations, J. Phys.: Condens. Matter, 2014, 26, 055004 CrossRef CAS PubMed.
- H. L. Peng, M. Z. Li, W. H. Wang, C.-Z. Wang and K. M. Ho, Effect of local structures and atomic packing on glass forming ability in CuxZr100−x metallic glasses, Appl. Phys. Lett., 2010, 96, 021901 CrossRef PubMed.
- S. Wu, M. Kramer, X. Fang, S. Wang, C. Wang, K. Ho, Z. Ding and L. Chen, Structural and dynamical properties of liquid Cu80Si20 alloy studied experimentally and by ab initio molecular dynamics simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 134208 CrossRef.
- B. Shen, C. Y. Liu, Y. Jia, G. Q. Yue, F. S. Ke, H. B. Zhao, L. Y. Chen, S. Y. Wang, C. Z. Wang and K. M. Ho, Molecular dynamics simulation studies of structural and dynamical properties of rapidly quenched Al, J. Non-Cryst. Solids, 2014, 383, 13–20 CrossRef CAS PubMed.
- M. Aykol, A. O. Mekhrabov and M. V. Akdeniz, Nano-scale phase separation in amorphous Fe–B alloys: Atomic and cluster ordering, Acta Mater., 2009, 57, 171–181 CrossRef CAS PubMed.
- R. N. Singh and F. Sommer, Segregation and immiscibility in liquid binary alloys, Rep. Prog. Phys., 1997, 60, 57–150 CrossRef CAS.
- F. Shimizu, S. Ogata and J. Li, Theory of shear banding in metallic glasses and molecular dynamics calculations, Mater. Trans., 2007, 48, 2923–2927 CrossRef CAS.
- J. T. Wang, P. D. Hodgson, J. D. Zhang, W. Y. Yan and C. H. Yang, Effects of pores on shear bands in metallic glasses: A molecular dynamics study, Comput. Mater. Sci., 2010, 50, 211–217 CrossRef CAS PubMed.
- K. Albe, Y. Ritter and D. Şopu, Enhancing the plasticity of metallic glasses: Shear band formation, nanocomposites and nanoglasses investigated by molecular dynamics simulations, Mech. Mater., 2013, 67, 94–103 CrossRef PubMed.
- J. S. C. Jang, S. R. Jian, C. F. Chang, L. J. Chang, Y. C. Huang, T. H. Li, J. C. Huang and C. T. Liu, Thermal and mechanical properties of the Zr53Cu30Ni9Al8 based bulk metallic glass microalloyed with silicon, J. Alloys Compd., 2009, 478, 215–219 CrossRef CAS PubMed.
- K.-W. Park, E. Fleury, H.-K. Seok and Y.-C. Kim, Deformation behaviors under tension and compression: Atomic simulation of Cu65Zr35 metallic glass, Intermetallics, 2011, 19, 1168–1173 CrossRef CAS PubMed.
- C. C. Wang and C. Wong, Different icosahedra in metallic glasses: stability and response to shear transformation, Scr. Mater., 2012, 66, 610–613 CrossRef CAS PubMed.
- A. Cao, Y. Cheng and E. Ma, Structural processes that initiate shear localization in metallic glass, Acta Mater., 2009, 57, 5146–5155 CrossRef CAS PubMed.
- H. L. Peng, M. Z. Li and W. H. Wang, Structural Signature of Plastic Deformation in Metallic Glasses, Phys. Rev. Lett., 2011, 106, 135503 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra03494a |
| This journal is © The Royal Society of Chemistry 2015 |