Evidence for changes on the lithium conduction dimensionality of Li0.5−yNayLa0.5Nb2O6 (0 ≤ y ≤ 0.5) perovskites
Abstract
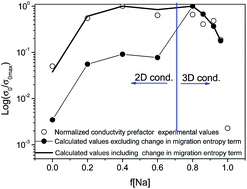
Li0.5−yNayLa0.5Nb2O6 samples (y = 0–0.5) were synthesized by the solid-state reaction (SSR). Structural features of the ap × ap × 2ap perovskite series were investigated by X-ray diffraction (XRD), nuclear magnetic resonance (NMR) and density functional theory DFT simulation techniques. The location of La ions was assessed by Rietveld analysis of XRD patterns, and structural sites occupied by Li, Na and Nb ions investigated by MAS-NMR spectroscopy. In Li-rich samples, La and Li ions are preferentially located at z/c = 0 planes, but as the Na content increases, La and Na occupy both z/c = 0 and 0.5 planes. To analyze La and Li possible arrangements, different structural models have been considered in DFT simulations, confirming the cation ordering deduced from XRD patterns and the impediment of Na ions to move through square windows of the perovskite. The structural information deduced has been used to discuss transport properties deduced by Impedance Spectroscopy (IS). In Li rich samples, the La arrangement in alternating planes favors a 2D-dimensional Li conductivity. The incorporation of Na in two crystallographic planes reduces La ordering and increases Li conductivity. La disorder favours the change from 2D to 3D Li conductivity, which could explain the broad maximum detected in the Li conductivity as a function of the Na content.

 Please wait while we load your content...
Please wait while we load your content...