Matrix-isolation and computational study of the HKrCCH⋯HCCH complex

Abstract

The HKrCCH⋯HCCH complex is identified in a Kr matrix with the H–Kr stretching bands at 1316.5 and 1305 cm⁻¹. The monomer-to-complex shift of the H–Kr stretching mode is about +60 cm⁻¹, which is significantly larger than that reported previously for the HXeCCH⋯HCCH complex in a Xe matrix (about +25 cm⁻¹). The HKrCCH⋯HCCH complex in a Kr matrix is formed at ∼40 K via the attachment of mobile acetylene molecules to the HKrCCH monomers formed at somewhat lower annealing temperatures upon thermally-induced mobility of H atoms (∼30 K). The same mechanism was previously proposed for the formation of the HXeCCH⋯HCCH complex in a Xe matrix. The assignment of the HKrCCH⋯HCCH complex is fully supported by the quantum chemical calculations. The experimental shift of the H–Kr stretching mode is comparable with the computational predictions (+46.6, +66.0, and +83.2 cm⁻¹ at the B3LYP, MP2, and CCSD(T) levels of theory, respectively), which are also bigger that the calculated shift in the HXeCCH⋯HCCH complex. These results confirm that the complexation effect is bigger for less stable noble-gas hydrides.

---

Introduction

Noble-gas hydrides represent interesting chemistry at low temperatures.¹ These molecules have the general formula HNgY where Ng is a noble-gas atom and Y is an electronegative fragment. Noble-gas hydrides are conventionally studied by matrix-isolation IR spectroscopy, which is helped by the very high absorption intensity of the H–Ng stretching mode. The typical method of preparation includes photolysis of the HY precursor in an Ng matrix and consequent annealing of the matrix, which mobilizes the fragments (usually H atoms) and leads to the diffusion-controlled reaction H + Ng + Y → HNgY. As suggested by quantum chemical calculations, all experimentally found HNgY molecules are lower in total energy than the H + Ng + Y asymptote.² One significant result was the preparation of fluorine-free organo-noble-gas molecules, the first representatives of which were HXeCCH and HKrCCH.^3–5

The HNgY molecules are relatively weakly bound and have large dipole moments, and this ensures a large effect upon interaction with other species.⁶ Another interesting feature of these interactions is a blue shift of the H–Ng stretching mode, as a rule observed in these experiments and predicted theoretically. This blue shift is explained by the complexation-induced enhancement of the charge separation (HNg)⁺Y⁻.⁶ A good number of HNgY complexes have been identified in matrices (see, for example, ref. 7–16) and much more structures have been studied computationally (see, for example, ref. 17–26).

The complexation effect becomes larger for less stable molecules as it has been demonstrated for a number of HXeY molecules with different Y groups, for example, for HXeCl, HXeBr, and HXeI interacting with water.¹⁶ The same trend is observed for HNgY molecules with the same Y and different Ng atoms. For example, interaction with nitrogen produces a larger effect on HArF than on HKrF,⁸ and interaction with HCl and nitrogen affects the properties of HKrCl more than the properties of HXeCl.^8,10,11,13 The experimental spectroscopic data are consistent with the quantum chemical calculations.^6–16

The studies of 1 : 1 HNgY⋯M complexes are connected to the possibility to stabilize the HNgY molecule in the M medium.²⁷ It is also possible that the complex units can react with each other or the interaction can destabilize the HNgY molecule. For example, the calculations show that the interaction with several water molecules destabilizes HXeOH.⁷ On the other hand, HXeCCH is predicted to be stable in acetylene clusters,²⁸ and the complexes of HXeCCH with one and two HCCH molecules have been identified in a Xe matrix.¹²

In the present work, we study the HKrCCH⋯HCCH complex to enlarge the amount of these interesting complexes identified experimentally. To our best knowledge, only a couple of computational works on the complexes of HKrCCH exist. Alkorta and Elguero studied interaction of HKrCCH with HF and HCl,¹⁷ and Mondal and Singh calculated the complexes of HKrCCH with H₂O, NH₃, CH₃OH and CH₃NH₂,²⁶ both at the MP2 level of theory. The case of HKrCCH is remarkable because this molecule has the weakest bonding among hydrides of Kr as judged by the lowest H–Kr stretching frequency, and it is interesting to test chemical stability of this complex and the magnitude of the complexation effect. The comparison with the previously identified HXeCCH⋯HCCH is also of interest. The experimental spectroscopic studies in a Kr matrix are supported by calculations at the B3LYP, MP2, and CCSD(T) levels of theory.

Quantum-chemical calculations

The molecular structures have been optimized using density functional theory with the B3LYP functional as implemented in the Gaussian package,^29–31 as well as the second-order perturbation theory (MP2) and the coupled-cluster CCSD(T) theory. For the DFT and MP2 calculations, the Gaussian09 program package is used.²⁹ The CCSD(T) calculations are performed with the CFOUR program.³² For all atoms, the def2-TZVPP basis sets are used.³³ Stationary points on the potential energy surface are characterized by harmonic vibrational frequency analyses at the used levels of theory. Anharmonic calculations are performed at the CCSD(T) level of theory by the VPT2 method implemented in the CFOUR program. The bonding analysis is carried out with the NBO 3.1 program implemented in the Gaussian09 program package. The values are obtained at 0 K, which is quite close to the conditions of the matrix experiments (4 K).

The parameters of the optimized structures of acetylene and HKrCCH are presented in Table 1. The bond distances of the HKrCCH monomer agree with the previous MP2 calculations.⁵ The B3LYP functional shows a shorter H–Kr bond and a longer Kr–C bond in HKrCCH compared with the CCSD(T) values. As expected, the MP2 method leads to shorter bonds compared with the CCSD(T) values. All methods result in a slightly longer C≡C bond for HKrCCH than in free acetylene. The total energy of the HKrCCH molecule is smaller than the sum of the H, Kr, and CCH energies by 27.3 (B3LYP), 58.0 (MP2), and 8.1 (CCSD(T)) kJ mol⁻¹ (ZPVE-corrected), which makes possible its formation at low temperatures. The difference between the formation energies is at least partially connected with difficulties to calculate the total energy of the CCH radical.²

Table 1 Structural parameters (in pm) of acetylene, HKrCCH, and HKrCCH⋯HCCH at different levels of theory^a,b

Species	Bond	B3LYP^b	MP2^b	CCSD(T)
a The indices indicate neighbouring atoms or numbering in the coordinated acetylene unit.b The basis set is def2-TZVPP.c The values in parenthesis are after the BSSE correction.d The C⋯H–C angle is 147.6° (147.9°) (B3LYP), 142.0° (140.7°) (MP2) and 142.4° (CCSD(T)).
HCCH	CH	106.2	105.9	106.1
	CC	119.7	120.9	120.7
HKrCCH	H–Kr	159.6	158.5	162.0
	Kr–C	228.0	222.2	226.3
	CC	121.1	122.6	122.3
	CH	106.4	106.2	106.4
HKrCCH⋯HCCH^c^,^d	H–Kr	158.1 (158.1)	156.3 (156.6)	159.3
	Kr–C	230.2 (230.1)	224.5 (224.2)	228.2
	CC	121.3 (121.3)	122.8 (122.8)	122.4
	CH	106.4 (106.4)	106.3 (106.3)	106.4
	CKrHcoord1	260.6 (261.5)	243.7 (250.9)	250.5
	Hcoord1Ccoord1	106.8 (106.8)	106.6 (106.5)	106.8
	Ccoord1Ccoord2	119.8 (119.8)	121.1 (121.0)	120.9
	Ccoord2Hcoord2	106.2 (106.2)	106.0 (105.9)	106.2

---

The calculated NPA charges are shown in Table 2. The bonding in noble-gas hydrides is usually described in terms of charge separation, namely (HKr)⁺(CCH)⁻.¹ This bonding motif is supported by the NPA charges which are +0.644e and −0.644e (MP2) for the HKr and CCH parts, respectively. In addition, the NBO analysis shows no bonding orbital for the Kr–C bond (see Fig. S1 in ESI†). However, there is a strong donor–acceptor interaction from a lone pair carbon orbital into the anti-bonding orbital of the H–Kr bond which accounts for 290.0 (B3LYP) and 500.8 (MP2) kJ mol⁻¹. These stabilization energies are obtained by delocalization of the charge from the localized occupied orbital into an empty orbital. The method is implemented in the NBO analysis and has been described elsewhere.³⁴ Within this ionic picture, the elongation of the C≡C bond can be explained by the charge delocalization from the formally negative C atom via the C≡C bond.

Table 2 Natural population charges (in elementary charges) of acetylene, HKrCCH, and HKrCCH⋯HCCH at the B3LYP and MP2 levels of theory^a,b

Species	Atom	B3LYP	MP2
a The indices indicate neighboring atoms or numbering in the coordinated acetylene unit.b The basis set is def2-TZVPP.
HCCH	H	0.230	0.228
	C	−0.230	−0.228
HKrCCH	HKr	−0.006	0.005
	Kr	0.547	0.639
	CKr	−0.392	−0.491
	C	−0.367	−0.366
	H	0.218	0.213
HKrCCH⋯HCCH	HKr	0.018	0.042
	Kr	0.552	0.645
	CKr	−0.408	−0.513
	C	−0.375	−0.379
	H	0.219	0.215
	Hcoord1	0.251	0.261
	Ccoord1	−0.229	−0.223
	Ccoord2	−0.256	−0.268
	Hcoord2	0.227	0.227

---

The calculated frequencies of the acetylene and HKrCCH monomers are given in Table 3. As for other noble-gas hydrides, the H–Kr stretching mode possesses the strongest absorption, and it will be considered in the analysis below. The H–Kr stretching frequencies of the HKrCCH monomer calculated in the harmonic approximation are 1650.5, 1601.9, and 1357.6 cm⁻¹ at the B3LYP, MP2, and CCSD(T) levels of theory. These frequencies are higher than the experimental value in a Kr matrix having the strongest absorption at 1241.5 cm⁻¹, and the CCSD(T) result, as expected, is the closest to the experimental value. The anharmonic contributions have been evaluated at the CCSD(T) level of theory, resulting in a frequency of 1125.5 cm⁻¹, which is lower than the experimental value. However, the anharmonic value may make sense because it refers to the molecule in vacuum whereas the experiment is performed in a solid matrix out of Kr atoms that have a relatively high interaction with the guest molecule. It is therefore most likely that the polarizable matrix enhances the charge separation in the molecule, blue-shifting the H–Ng stretching mode. This effect is predicted for a number of HNgY molecules by the polarized continuum model,³⁵ DFT calculations in noble-gas clusters,³⁶ and hybrid quantum-classical simulations,^37,38 although an opposite opinion has been derived from the MP4 method.³⁹

Table 3 Calculated harmonic frequencies (in cm⁻¹) of acetylene, HKrCCH, and HKrCCH⋯HCCH at different levels of theory^a,b

Mode	Symmetry	B3LYP	MP2	CCSD(T)	Assignment
a The def2-TZVPP basis sets is used for all atoms.b The intensities in parenthesis are in km mol^−1.
HCCH
ν1	∑g	3518.1 (0)	3549.1 (0)	3513.7 (0)	Sym. CH stretch
ν2	∑g	3419.3 (90)	3456.0 (95)	3415.3 (82)	Asym. CH stretch
ν3	∑g	2071.4 (0)	1982.5 (0)	2007.1 (0)	CC stretch
ν4	Πg	658.8 (0)	616.9 (0)	609.8 (0)	Asym. CCH bend
ν5	Πu	770.2 (104)	766.4 (95)	763.7 (94)	Sym. CCH bend
HKrCCH
ν1	∑	3445.3 (42)	3464.9 (35)	3440.1 (36)	CH stretch
ν2	∑	2067.4 (3)	1967.2 (8)	2007.1 (1)	CC stretch
ν3	∑	1650.5 (1441)	1601.9 (2190)	1357.6 (2262)	Kr–H stretch
ν4	∑	296.6 (150)	329.2 (186)	310.5 (106)	Kr–C stretch
ν5	Π	679.6 (35)	703.5 (41)	673.3 (9)
ν6	Π	695.7 (16)	736.5 (6)	691.5 (38)
ν7	Π	119.8 (20)	133.2 (19)	136.8 (16)
HKrCCH⋯HCCH
ν1	A′	19.6 (2)	39.7 (2)	34.8 (2)
ν2	A′	73.7 (1)	79.9 (1)	78.7 (0)
ν3	A′	110.6 (1)	124.9 (3)	118.1 (1)
ν4	A′	139.8 (29)	165.4 (27)	164.1 (24)
ν5	A′	290.2 (136)	317.1 (192)	305.5 (123)	Kr–C stretch
ν6	A′	680.7 (11)	642.7 (4)	633.4 (3)
ν7	A′	685.6 (7)	734.7 (5)	680.3 (8)
ν8	A′	698.0 (40)	709.6 (37)	697.3 (36)
ν9	A′	819.1 (105)	817.3 (118)	810.5 (116)
ν10	A′	1697.1 (1301)	1667.9 (2018)	1440.8 (2205)	Kr–H stretch
ν11	A′	2058.1 (8)	1958.6 (9)	1995.7 (5)	CC stretch
ν12	A′	2060.5 (2)	1967.2 (4)	2001.2 (2)	CC stretch
ν13	A′	3361.0 (217)	3380.9 (207)	3361.0 (173)	Asym. CH stretch in HCCH
ν14	A′	3441.6 (43)	3459.8 (36)	3435.0 (37)	CH stretch in HKrCCH
ν15	A′	3492.9 (3)	3515.4 (5)	3487.7 (3)	Sym. CH stretch in HCCH
ν16	A′′	84.2 (1)	81.0 (0)	79.9 (0)
ν17	A′′	124.6 (19)	141.0 (19)	142.9 (17)
ν18	A′′	676.2 (28)	634.4 (5)	623.6 (5)
ν19	A′′	678.6 (8)	710.2 (37)	680.7 (10)
ν20	A′′	691.6 (20)	736.6 (3)	698.0 (30)
ν21	A′′	810.7 (84)	798.6 (80)	792.2 (79)

---

The optimized structure of the HKrCCH⋯HCCH complex is presented in Fig. 1 and Table 1, and it is similar to the previous calculations of the HXeCCH⋯HCCH complex.¹² Interaction with acetylene enhances the charge separation in HKrCCH, which is similar to the previous results on the HNgY complexes. For example, the charge of the HKr part increases from +0.644e to +0.697e (MP2). The complex formation leads to a slight weakening of the Kr–C bond and a strengthening of the H–Kr bond (the bond lengths change by +0.96 and −0.94%, respectively). These changes are larger than the LMP2/AVTZ values obtained for the corresponding bonds of the HXeCCH⋯HCCH complex (+0.86 and −0.69%), which can be explained by a stronger bonding in HXeCCH.

Fig. 1 Optimized structure of the HKrCCH⋯HCCH complex. The structural parameters and the atomic charges at different levels of theory are shown in Tables 1 and 2.

The interaction energy of the HKrCCH⋯HCCH complex (CCSD(T)) obtained as a difference of the total energies of the complex and the monomers is −16.2 kJ mol⁻¹ (−13.4 kJ mol⁻¹ after ZPVE correction). The ZPE-corrected interaction energies at the B3LYP and MP2 levels are −7.6 and −16.4 kJ mol⁻¹ and they are −7.2 and −13.4 kJ mol⁻¹ after BSSE corrections. In comparison, the interaction energy of the HXeCCH⋯HCCH complex was reported to be −14.9 kJ mol⁻¹ (LMP2/AVTZ, without ZPVE and BSSE correction).¹² The interaction in the HKrCCH⋯HCCH complex seems to be stronger than in the HCCH dimer characterized by interaction energies of −7.1 (B3LYP) and −3.8 (MP2) kJ mol⁻¹.⁴⁰ This difference is probably explained by a large dipole moment of HKrCCH (3.47, 4.87, and 2.98 D at the B3LYP, MP2 and CCSD(T) levels), which leads to the dipole–quadrupole interaction in the HKrCCH⋯HCCH complex. It has been recently discussed that the HKrCCH complexes with some molecules are stronger than the corresponding HCCH complexes.²⁶

The BSSE correction at the CCSD(T) level is expected to be of the same order as for the MP2 calculation or slightly higher. Neglecting the error leads to very small changes in the structure of the complex (see Table 1), except for the distance to the coordinating acetylene, which is substantially longer after BSSE correction. Therefore, the interaction is somewhat weakened after BSSE correction and the change of the interaction energy is supposed to be similar to the ZPVE energy. However, our assignment is based on the monomer-to-complex shift of the H–Kr stretching frequency, and this frequency is only slightly changed by BSSE correction (by −2.0 and −7.1 cm⁻¹ at the B3LYP and MP2 levels). Since this correction does not change the results significantly, we will not further consider it. Furthermore, the influence of the entropy on the HKrCCH⋯HCCH formation is expected to be quite small at cryogenic conditions and accounts only for 2 kJ mol⁻¹ at 40 K. On the other hand, the entropic effect is not negligible at standard conditions (298 K, 1 atm), for which the reaction enthalpy is still calculated to be exothermic by −6.9 kJ mol⁻¹ but the Gibbs enthalpy is +14.3 kJ mol⁻¹.

As the main spectroscopic fingerprint of the complex formation, the calculated frequency of the H–Kr stretching mode is increased, as typical for the HNgY complexes.⁶ The harmonic monomer-to-complex frequency shift is +46.6, +66.0, and +83.2 cm⁻¹ at the B3LYP, MP2, and CCSD(T) levels of theory, respectively. These spectral shifts are significantly larger than the LMP2/AVTZ value reported by Domanskaya et al. for the HXeCCH⋯HCCH complex (+34 cm⁻¹).¹² The intensity of the H–Kr stretching mode somewhat decreases upon complexation due to the increase of the positive charge of this part, and this is also similar to the studies of other HNgY complexes.⁶

We also calculated the HKrCCH⋯(HCCH)₂ complex at the B3LYP and MP2 levels of theory. Its structure is similar to that of the HXeCCH⋯(HCCH)₂ complex reported previously (see Fig. S2 in ESI†).¹² The calculated H–Kr stretching frequencies are 1741.9 (B3LYP) and 1737.3 (MP2) cm⁻¹, which are higher by 44.8 and 69.8 cm⁻¹ than those of the HKrCCH⋯HCCH complex. These shifts are comparable with the monomer-to-complex shifts calculated for the HKrCCH⋯HCCH complex. The interaction energy of HKrCCH⋯(HCCH)₂ complex changes by −7.2 (B3LYP) and −16.5 (MP2) kJ mol⁻¹ compared to that of HKrCCH⋯HCCH, which is similar to the case of HXeCCH⋯(HCCH)₂.

Experiment

The gas mixtures of acetylene (≥99%) and krypton (≥99.999%, AGA) were made in a glass bulb with the HCCH/Kr concentration ratios of 1/300, 1/500, 1/1000, and 1/2000. The HCCH/Kr matrices were deposited onto a CsI substrate at 20, 25, 27, and 30 K in a closed-cycle helium cryostat (RDK-408D2, SHI). Some matrices with the 1/300 concentration ratio were deposited at 15 K. The IR absorption spectra in the 4000–600 cm⁻¹ range were measured at 4.3 K with an FTIR spectrometer (Vertex 80V, Bruker) with 1 cm⁻¹ resolution co-adding 500 scans. The matrices were photolyzed by an excimer laser (MSX-250, MPB) operating at 193 nm (∼10 mJ cm⁻²). Typical percentage of the decomposition of HCCH was 15–25% after 1800 pulses. It seems that the full decomposition of acetylene in a Kr matrix is limited by the self-limitation of photolysis.⁴¹ This effect is caused by species produced in the matrix during the photolysis and absorbing the 193 nm light. The annealing-induced products were decomposed by light from a mercury lamp (254 nm) and in some experiments with an argon-ion laser (488 nm).

Acetylene monomer has the strongest bands in a Kr matrix at 3293.3 and 3280.1 cm⁻¹ (Fermi components of the CH stretching mode) and at 732.2 cm⁻¹ (CCH bending mode) as reported previously.⁴² Acetylene dimer absorbs at 3278 and 3257 cm⁻¹ and at 746 and 742 cm⁻¹, which is consistent with the experiments in an Ar matrix reported by Golovkin et al.⁴⁰ The amount of higher aggregates of acetylene increase with the acetylene concentration and deposition temperature.

193 nm light decomposes acetylene and produces CCH radicals (doublet at 1842 and 1844 cm⁻¹) and H atoms. Presumably, CC molecules are also formed upon decomposition of CCH radicals; however, they are invisible for IR spectroscopy in a Kr matrix. The formation of KrHKr⁺ ions (852 and 1008 cm⁻¹)⁴³ and C₄ molecules (1539 cm⁻¹)⁴⁴ is also observed especially in matrices with higher acetylene concentrations and for higher deposition temperatures. We did not obtain evidence of the formation of the CCH⋯HCCH complex as a result of photolysis, presumably indicating a negligible amount of this species, and this is discussed later.

Upon thermal annealing above ∼25 K, H atoms globally move in a Kr matrix⁴⁵ and can react with the Kr + CCH centers forming HKrCCH. This formation mechanism has been supported by electron paramagnetic resonance experiments.⁴⁶ HKrCCH has the main H–Kr stretching bands at 1241.5, 1249.5, and 1257 cm⁻¹ (Fig. 2a), the CH stretching band at 3290 cm⁻¹, and the CCH bending band at 610 cm⁻¹.⁵ Other annealing products are C₂H₃ (1353.2 and 896.6 cm⁻¹)^47,48 and C₄H (2055.2 cm⁻¹)⁴⁹ formed in the H + HCCH and H + C₄ reactions, respectively. In addition, the amount of CCH radicals increases as a result of annealing (typically by 30–50%), indicating the H + CC reaction. It is worth noting that no recovery of CCH is observed in similar experiments in a Xe matrix, which is due to the formation of HXeCC,³ whereas HKrCC is unstable. The HKrCCH bands are easily decomposed by UV light from a mercury lamp (Fig. 2a) and more slowly by 488 nm light. These “decomposition” spectra are mainly used in the analysis because they are less affected by other species present in the matrix compared to the “annealing” spectra. The amount of CCH radicals increases when HKrCCH is decomposed (by ∼10%), which supports this assignment.

Fig. 2 (a) HKrCCH in a Kr matrix in the H–Kr stretching region. The upper curve is a difference FTIR spectrum showing the result of annealing at 40 K of an HCCH/Kr (1/500) matrix deposited at 20 K and photolyzed at 193 nm. The lower curve is a difference spectrum showing the result of decomposition of HKrCCH by a mercury lamp. The insert shows the enlarged bands in the 1323 to 1284 cm⁻¹ region. The bands assigned to the HKrCCH⋯HCCH complex are marked by C. The band marked by an arrow belongs to HKrC₄H. The strong signal at ∼1325 cm⁻¹ is due to acetylene absorption. The spectra were measured at 4.3 K. (b) The amount of HKrCCH molecules relative to the initial amount of HCCH monomers for different deposition temperatures and matrix ratios.

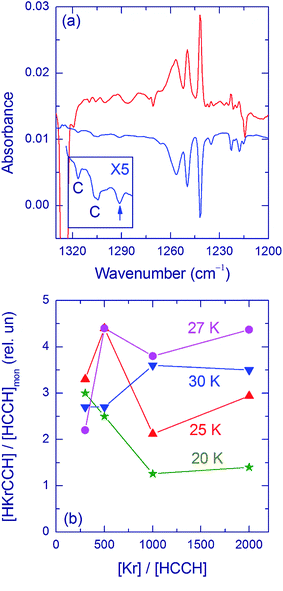
The H–Kr stretching bands of HKrCCH show an extensive structure (Fig. 2a); in addition to the main bands at 1241.5, 1249.5, and 1257 cm⁻¹, a number of weaker bands appear in the region around 1220 cm⁻¹. These bands have the same intensity ratio in different experimental conditions (HCCH/Kr concentration ratio and deposition temperature), and they have been assigned to the HKrCCH monomer in various matrix sites.⁵ Fig. 2b presents the amount of HKrCCH normalized by the amount of acetylene monomer after deposition for different deposition temperatures and matrix ratios. There are numerous experimental difficulties that make this analysis somewhat uncertain; however, the main trends can be understood. For HCCH/Kr = 1/300, the deposition temperature has a small effect on the relative amount of HKrCCH after photolysis and annealing whereas the difference becomes bigger for lower acetylene concentrations. The relative amount of HKrCCH is smaller for deposition at 20 K, and it seems to be maximal for ∼27 K.

Two additional bands, also originating from HKrCCH, are observed at 1316.5 and 1305 cm⁻¹ (Fig. 2a). These bands are easily bleached by light from a mercury lamp with the efficiency similar to that of the HKrCCH monomer bands. These bands are assigned to the HKrCCH⋯HCCH complex (a band at 1291 cm⁻¹ marked with an arrow is discussed below). The bands at 1316.5 and 1305 cm⁻¹ are much weaker than the HKrCCH monomer bands; however, they are reproducible and reliably identified in the decomposition spectra (see the insert in Fig. 2a). The intensity of these bands, relative to the HKrCCH monomer bands, changes in different experiments. In particular, the HKrCCH monomer appears at annealing somewhat below 30 K whereas the HKrCCH⋯HCCH complex is formed for annealing at higher temperatures (Fig. 3a). This fact suggests that the complex is formed by attaching thermally mobilized acetylene molecules to the HKrCCH monomers. The thermally-induced mobility of acetylene in the matrix is evidenced by the formation of acetylene agglomerates under these experimental conditions (Fig. 3b). In these experiments, we did not find bands suitable for the HKrCCH⋯(HCCH)₂ complex. The amount of this trimer should be very small and the present signal-to-noise ratio is not sufficient for its identification.

Fig. 3 Effect of the annealing temperature. (a) Decomposition spectra in the H–Kr stretching region for HCCH/Kr (1/1000) matrices deposited at 20 K and annealed at 30 and 40 K (two different experiments). The bands of HKrCCH are equalized for better presentation. The HKrCCH⋯HCCH bands are marked by C. The matrices were first photolyzed at 193 nm. (b) Difference spectra (annealing minus photolysis) in the acetylene stretching region for HCCH/Kr (1/1000) matrices deposited at 20 K and annealed at 30 and 40 K (the same matrix). Also shown a spectrum for an HCCH/Kr (1/1000) matrix deposited at 27 K and annealed at 40 K. The spectra were measured at 4.3 K.

The formation of the HKrCCH⋯HCCH complex is found to be less efficient in matrices deposited at temperatures higher than 20 K (Fig. 4a). In accord with the proposed formation mechanism, the mobility of acetylene is found to be less extensive for deposition at the higher temperatures (Fig. 3b). The mechanism of mobility of acetylene in a Kr matrix is unknown. It can be speculated that it involves matrix defects similarly to mobility of species in various solids (vacancy-assisted diffusion).^50–53 For higher-temperature deposition, the matrix has less defects, which may slow down the mobility of acetylene. In addition, the attaching of acetylene to HKrCCH may also be less efficient in more compact matrix morphologies.

Fig. 4 Effect of the deposition temperature. (a) Decomposition spectra in the H–Kr stretching region for HCCH/Kr (1/1000) matrices deposited at 20 and 27 K and annealed at 40 K. The HKrCCH⋯HCCH bands are marked by C. The band of HKrC₄H is marked by an arrow. The matrices were first photolyzed at 193 nm. The bands of HKrCCH are equalized for better presentation. (b) Spectra in the acetylene stretching region for HCCH/Kr (1/1000) matrices measured after deposition at 20 and 27 K. The bands of acetylene dimer are marked by dots. The insert shows the amount of HKrC₄H (normalized by the amount of HKrCCH) versus the amount of acetylene dimers (normalized by the amount of acetylene monomers). The data are obtained for different deposition temperatures and HCCH/Kr concentration ratios (up triangles with 1/2000; stars with 1/1000; circles with 1/500; down triangles with 1/300). The spectra were measured at 4.3 K.

It is seen that for deposition at higher temperature, an additional band at 1291 cm⁻¹ rises after photolysis and annealing (Fig. 4a). It is practically absent in matrices deposited at 15 and 20 K and its intensity relative to the HKrCCH monomer bands tends to increase with the deposition temperature. This band appears together with the HKrCCH monomer bands upon annealing above ∼25 K and its intensity saturates together with the HKrCCH monomer bands upon annealing at ∼30 K; thus, its formation is connected with the thermal mobility of H atoms. Annealing at higher temperatures (35 and 40 K) does not increase this band, similarly to the HKrCCH monomer bands. The 1291 cm⁻¹ band is bleached by light from a mercury lamp.

The analysis shows that the relative intensity of the 1291 cm⁻¹ band correlates well with the amount of acetylene dimers observed after matrix deposition (Fig. 4b and the insert). Based on this concentration dependence, the 1291 cm⁻¹ band might be thought to belong to the HKrCCH⋯HCCH complex formed from the CCH⋯HCCH complex, i.e. by the formation mechanism of most of the HNgY complexes.^6,54 However, we cannot assign the 1291 cm⁻¹ band to the HKrCCH⋯HCCH complex. Instead, this band presumably originates from HKrC₄H molecules formed in the H + Kr⋯C₄H reaction.⁵⁵ When the 1291 cm⁻¹ band is strong enough, we can see the weak satellites at 1317, 1307.5, and 1275.5 cm⁻¹ previously also assigned to HKrC₄H. It should be noted that C₄H radicals are not formed upon photolysis, in contrast to CCH radicals. This fact can be connected with their efficient photodecomposition at 193 nm. Instead, C₄H radicals (2055 cm⁻¹) are formed upon thermally-induced mobility of H atoms in the H + C₄ reaction and their concentration increases in matrices with higher concentration of acetylene dimers.

One additional factor may be important for the relative decrease of the HKrC₄H amount in matrixes deposited at low temperatures. The formation of HKrC₄H requires reaction of two mobile H atoms with a Kr⋯C₄ center, i.e. losses of H atoms are crucial for its formation. It follows that various defects in the matrix can strongly decrease the amount of annealing-produced HKrC₄H molecules as discussed elsewhere for some other noble-gas hydrides.⁵⁶ The formation efficiency of HKrCCH is smaller for deposition at 20 K when a matrix contains more defects (Fig. 2b), and this effect should be even stronger for HKrC₄H. For HCCH/Kr = 300, the deposition temperature does not affect much the concentration of HKrCCH (Fig. 2b), which means that the high precursor concentration also reduces the efficiency of H-atom mobility.⁵⁶ This explains why the amount of HKrC₄H is not maximal for the highest acetylene concentration (insert in Fig. 4b).

Concluding discussion

In the present work, we have identified the HKrCCH⋯HCCH complex with the H–Kr stretching bands at 1316.5 and 1305 cm⁻¹. The monomer-to-complex shift of the H–Kr stretching mode is ∼60 cm⁻¹ if the distances from the strongest monomer bands are averaged. This monomer-to-complex shift is significantly larger than that reported previously for the HXeCCH⋯HCCH complex (∼25 cm⁻¹),¹² which is most probably connected with weaker bonding of HKrCCH. The HKrCCH⋯HCCH complex is formed at ∼40 K presumably via the attachment of mobile acetylene molecules to the HKrCCH monomers formed at somewhat lower annealing temperatures (∼30 K). This mechanism is supported by the simultaneous increase of the amounts of the HKrCCH⋯HCCH complexes and acetylene agglomerates upon annealing. The HKrCCH⋯HCCH complex is obtained in quite small amounts, which prevents us from identification of other vibrational transitions with lower absorption intensity, which is actually typical for experiments on HNgY complexes.⁶ The weak signals are also the reason why the HKrCCH⋯(HCCH)₂ complex is not found in the present study. The preparation of the HKrCCH⋯HCCH complex from acetylene dimers has failed. When a deposited matrix contains a considerable amount of acetylene dimers, the amount of HKrCCH⋯HCCH complexes decreases and HKrC₄H is formed instead as a result of photolysis and annealing.

The same formation mechanism was previously proposed for the HXeCCH⋯HCCH complex.¹² Xe matrices containing mainly monomeric acetylene were photolyzed at 193 nm. Annealing at ∼40 K mobilizes H atoms in a Xe matrix and leads to the formation of HXeCCH monomers. Annealing above 50 K mobilizes acetylene molecules, which produces the HXeCCH⋯HCCH complex. Similarly to the present experiments, in HCCH/Xe matrices containing acetylene dimers, photolysis and annealing did not lead to the formation of the HXeCCH⋯HCCH complexes, and this indirectly supports our present assignment.

It is interesting that 193 nm photolysis of acetylene dimers in Kr and Xe matrices does not lead to the CCH⋯HCCH complexes required for the formation of the HNgCCH⋯HCCH complexes upon thermally-induced mobility of H atoms.^6,54 The negligible amount of the CCH⋯HCCH complex after UV photolysis can be connected with in-cage photochemical reactions. If the photogenerated H atom remains in the cage, it can, in addition to the recovery of acetylene, lead to unwanted reactions. It should be reminded that the cage exit probability of an H atom is presumably very small because of the small excess energy available in 193 nm photolysis of acetylene (≤0.7 eV). Indeed, for photolysis of HCl in a Kr matrix with excess energy of 3 eV, the cage exit probability is only 5%.⁵⁷ The important role of in-cage reactions is supported by the experiments with HCCH/Xe/Kr matrices, in which the amount of the CCH⋯Xe complex after UV photolysis was quite detectable, and the amount of HXeCCH in a Kr matrix after annealing at 30 K was comparable to that of HKrCCH.⁵⁸

The assignment of the 1316.5 and 1305 cm⁻¹ bands to the HKrCCH⋯HCCH complex is fully supported by the quantum chemical calculations. The experimental shift of the H–Kr stretching mode (about +60 cm⁻¹) is comparable with the computational predictions (+46.6, +66.0, and +83.2 cm⁻¹ at the B3LYP, MP2, and CCSD(T) levels of theory, respectively). Both theoretically and experimentally, this spectral shift is significantly larger than the values previously obtained for the HXeCCH⋯HCCH complex whereas the calculated structures and interaction energies are similar. This confirms that the complexation effect is bigger for less stable HNgY molecules.

Acknowledgements

KW acknowledges the German Academic Exchange Service for the travel grant to the University of Helsinki. TV thanks the Fond der Chemischen Industrie for financial support and Prof. Krossing for computational resources. This work is also a part of the Project KUMURA of the Academy of Finland (no. 1277993). Susy Lopes and Cheng Zhu are thanked for technical assistance and Vladimir Feldman for useful comments.

Notes and references

1. L. Khriachtchev, M. Räsänen and R. B. Gerber, Acc. Chem. Res., 2009, 42, 183–191.
2. A. Lignell, L. Khriachtchev, J. Lundell, H. Tanskanen and M. Räsänen, J. Chem. Phys., 2006, 125, 184514.
3. L. Khriachtchev, H. Tanskanen, J. Lundell, M. Pettersson, H. Kiljunen and M. Räsänen, J. Am. Chem. Soc., 2003, 125, 4696–4697.
4. V. I. Feldman, F. F. Sukhov, A. Yu. Orlov and I. V. Tyulpina, J. Am. Chem. Soc., 2003, 125, 4698–4699.
5. L. Khriachtchev, H. Tanskanen, A. Cohen, R. B. Gerber, J. Lundell, M. Pettersson, H. Kiljunen and M. Räsänen, J. Am. Chem. Soc., 2003, 125, 6876–6877.
6. A. Lignell and L. Khriachtchev, J. Mol. Struct., 2008, 889, 1–11.
7. A. V. Nemukhin, B. L. Grigorenko, L. Khriachtchev, H. Tanskanen, M. Pettersson and M. Räsänen, J. Am. Chem. Soc., 2002, 124, 10706–10711.
8. A. Lignell, L. Khriachtchev, M. Pettersson and M. Räsänen, J. Chem. Phys., 2003, 118, 11120–11128.
9. H. Tanskanen, S. Johansson, A. Lignell, L. Khriachtchev and M. Räsänen, J. Chem. Phys., 2007, 127, 154313.
10. A. Lignell, J. Lundell, L. Khriachtchev and M. Räsänen, J. Phys. Chem. A, 2008, 112, 5486–5494.
11. A. Corani, A. Domanskaya, L. Khriachtchev, M. Räsänen and A. Lignell, J. Phys. Chem. A, 2009, 113, 10687–10692.
12. A. Domanskaya, A. V. Kobzarenko, E. Tsivion, L. Khriachtchev, V. I. Feldman, R. B. Gerber and M. Räsänen, Chem. Phys. Lett., 2009, 481, 83–87.
13. L. Khriachtchev, S. Tapio, M. Räsänen, A. Domanskaya and A. Lignell, J. Chem. Phys., 2010, 133, 084309.
14. M. Tsuge, S. Berski, R. Stachowski, M. Räsänen, Z. Latajka and L. Khriachtchev, J. Phys. Chem. A, 2012, 116, 4510–4517.
15. M. Tsuge, S. Berski, M. Räsänen, Z. Latajka and L. Khriachtchev, J. Chem. Phys., 2013, 138, 104314.
16. M. Tsuge, S. Berski, M. Räsänen, Z. Latajka and L. Khriachtchev, J. Chem. Phys., 2014, 140, 044323.
17. I. Alkorta and J. Elguero, Chem. Phys. Lett., 2003, 381, 505–511.
18. S. Y. Yen, C. H. Mou and W. P. Hu, Chem. Phys. Lett., 2004, 383, 606–611.
19. S. A. C. McDowell and A. D. Buckingham, Spectrochim. Acta, Part A, 2005, 61, 1603–1609.
20. S. A. C. McDowell, Curr. Org. Chem., 2006, 10, 791–803.
21. J. Cukras and J. Sadlej, Chem. Phys. Lett., 2008, 459, 44–48.
22. J. Cukras and J. Sadlej, Phys. Chem. Chem. Phys., 2011, 13, 15455–15467.
23. Q. Z. Li, J. L. Zhao, B. Jing, R. Li, W. Z. Li and J. B. Cheng, J. Comput. Chem., 2011, 32, 2432–2440.
24. J. Jankowska and J. Sadlej, Chem. Phys. Lett., 2011, 517, 155–161.
25. M. D. Esrafili, S. Shahabivand and E. Vessally, Comput. Theor. Chem., 2013, 1020, 1–6.
26. S. Mondal and P. C. Singh, RSC Adv., 2014, 4, 20752–20760.
27. R. B. Gerber, E. Tsivion, L. Khriachtchev and M. Räsänen, Chem. Phys. Lett., 2012, 545, 1–8.
28. E. Tsivion and R. B. Gerber, Phys. Chem. Chem. Phys., 2010, 12, 19601–19606.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian09, Gaussian Inc., Wallingford CT, 2009.
30. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
31. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
32. J. F. Stanton, J. Gauss, M. E. Harding, P. G. Szalay, A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, L. Cheng, O. Christiansen, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, D. A. Matthews, T. Metzroth, L. A. Mück, D. P. O'Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang and J. D. Watts, CFOUR 1.2, ed., Mainz, 2010.
33. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
34. A. E. Reed, L. A. Curtis and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
35. M. Tsuge, A. Lignell, M. Räsänen and L. Khriachtchev, J. Chem. Phys., 2013, 139, 204303.
36. A. Cohen, M. Tsuge, L. Khriachtchev, M. Räsänen and R. B. Gerber, Chem. Phys. Lett., 2014, 594, 18–22.
37. K. Niimi, A. Nakayama, Y. Ono and T. Taketsugu, J. Phys. Chem. A, 2014, 118, 380–387.
38. C. Zhu, K. Niimi, T. Taketsugu, M. Tsuge and L. Khriachtchev, J. Chem. Phys., 2015, 142, 054305.
39. J. Kalinowski, R. B. Gerber, M. Räsänen, A. Lignell and L. Khriachtchev, J. Chem. Phys., 2014, 140, 094303.
40. A. V. Golovkin, D. I. Davlyatshin, A. L. Serebrennikova and L. V. Serebrennikov, J. Mol. Struct., 2013, 1049, 392–399.
41. L. Khriachtchev, M. Pettersson and M. Räsänen, Chem. Phys. Lett., 1998, 288, 727–733.
42. H. Tanskanen, L. Khriachtchev, J. Lundell and M. Räsänen, J. Chem. Phys., 2004, 121, 8291–8298.
43. V. E. Bondybey and G. C. Pimentel, J. Chem. Phys., 1972, 56, 3832–3836.
44. J. Szczepanski, S. Ekern, C. Chapo and M. Vala, Chem. Phys., 1996, 211, 359–366.
45. L. Khriachtchev, M. Saarelainen, M. Pettersson and M. Räsänen, J. Chem. Phys., 2003, 118, 6403–6410.
46. S. V. Kameneva, A. V. Kobzarenko and V. I. Feldman, Radiat. Phys. Chem., 2015, 110, 17–23.
47. R. A. Shepherd, T. J. Doyle and W. R. M. Graham, J. Chem. Phys., 1988, 89, 2738–2742.
48. H. Tanskanen, L. Khriachtchev, M. Räsänen, V. I. Veldman, F. F. Sukhov, A. Y. Orlov and D. A. Tuyrin, J. Chem. Phys., 2005, 123, 064318.
49. K. I. Dismuke, W. R. M. Graham and W. Weltner Jr, J. Mol. Spectrosc., 1975, 57, 127–137.
50. R. O. Simmons, Mater. Chem. Phys., 1997, 50, 124–132.
51. H. Bracht, E. E. Haller and R. Clark-Phelps, Phys. Rev. Lett., 1998, 81, 393–396.
52. C. Melis, G. M. Lopez and V. Fiorentini, Appl. Phys. Lett., 2004, 85, 4902–4904.
53. M. D. McCluskey and E. E. Haller, Dopants and Defects in Semiconductors, CRC Press, 2012.
54. L. Khriachtchev, J. Phys. Chem. A, 2015, 119, 2735–2746.
55. H. Tanskanen, L. Khriachtchev, J. Lundell, H. Kiljunen and M. Räsänen, J. Am. Chem. Soc., 2003, 125, 16361–16366.
56. H. Tanskanen, L. Khriachtchev, A. Lignell, M. Räsänen, S. Johansson, I. Khyzhniy and E. Savchenko, Phys. Chem. Chem. Phys., 2008, 10, 692–710.
57. M. Dickgiesser and N. Schwentner, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 168, 252–267.
58. H. Tanskanen, L. Khriachtchev, J. Lundell and M. Räsänen, J. Chem. Phys., 2006, 125, 074501.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra01880c

---