Diradical ring closing reactions displaying Woodward–Hoffmann behaviour and torquoselectivity

Abstract

The symmetry rules enunciated in 1965 by Woodward and Hoffmann govern pericyclic reactions. They have been successfully applied to a wealth of concerted reactions showing exceptional predictive power and control. In this communication, we present evidence of reminiscent orbital control, analogue to that described by Woodward–Hoffmann (WH), dictating the course of diradical reactions. In this regard, the frontiers of application of these symmetry rules may be broader than what is commonly recognized.

---

In 1965 Woodward and Hoffmann published what probably was one of the greatest advances in the field of physical organic chemistry in the XX century. The symmetry rules that govern pericyclic reactions allowed chemists not only to understand processes earlier considered non-mechanism reactions¹ but also to anticipate product formation with a degree of control unseen until that moment.² These rules allow the prediction of a preferred product formation often including chemo-, peri- and stereoselectivity.

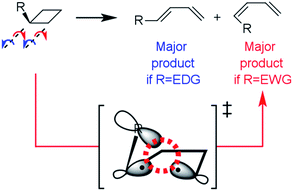
Twenty years later, Dolbuer and Houk observed that pericyclic reactivity operates under such a stringent orbital control that there is still a further level of selectivity that can be layered on top of the Woodward–Hoffmann (WH) rules.³ This selectivity is often exemplified with the ring opening of substituted cyclobutenes where two WH-allowed conrotatory pathways afford either the E- or the Z-1,3-butadiene isomers, depending on the electronic nature of the substituent (see Fig. 1).

Fig. 1 Electron donating groups (EDG) afford the E-1,3-butadiene as anticipated due to steric effects. However, electron withdrawing groups (EWG) feature a favourable two-electron in three orbital interaction that overcomes the steric contacts reversing the product distribution.

Pericyclic reactions seemingly follow the WH rules with essentially no exceptions. We have been interested, along with other research groups, in exploring whether exceptions may actually occur and, if they occur, what are the conditions that make them possible. In order to look for such rare reactions we decided to stretch academic examples of pericyclic reactivity in different directions and check for the frontiers of applicability of the WH rules. In this search, we found that pericyclic reactions, generally speaking, never follow WH forbidden pathways. In turn, when forced to follow formally symmetry forbidden paths, molecular systems avoid pericyclicity in various ways:

(1) Single-step, concerted reactions become multistep processes circumventing the applicability of symmetry rules.⁴

(2) Formally forbidden products arise from allowed transition states on reactions where dramatic direction changes of the reaction coordinate occur after the transition state.⁵

(3) Reactions of systems containing lone pairs can become pseudopericyclic.⁶

(4) Transition states become strongly diradical and depart from the closed shell symmetry constraints.⁷

Surprisingly, during our work on the five-member ring closure of vinyl-allene oxides⁸ and their aza isoelectronic derivatives⁹ via diradical collapse, we found that the stereospecific ring closure observed for these species could be related to the number of π electrons in the ring, very much in connection with the rationale of the WH rules. This observation has led us to explore whether strong orbital control that could be attributed to conjugated diradical species, in analogy to pericyclic processes, actually exists.

To study this connection, we decided to use the vinylogous trimethylenemethane system A1 as a parent compound, together with the vinyl allene oxide and its aza analogue, whose reactivity has been extensively studied in our group (Fig. 2). Following the same rationale that we employed to explain the stereospecificity in ref. 8, we assumed that the diradical collapse of the non-polarized A1 system occurs involving 5 π electrons. This is what can be expected from a pure diradical.^5a The inclusion of electronegative nuclei in the cyclic backbone polarizes the diradical so that the forming ring system becomes electron rich at the expense of the exocyclic methylene. In this scenario, it is expected that the more electronegative the substituent is, the closer the ring system approaches to featuring 6 π electrons. These electron rich systems should therefore favour the disrotatory pathway, corresponding to the WH-allowed electrocyclization of 6 π electron compounds.

Fig. 2 Trimethylenemethane diradical and the three vinylogous systems whose diradical ring closure has been studied in this work.

All the stationary points involved in this chemistry were computed within the density functional theory scheme.¹⁰ The meta-hybrid exchange–correlation functional, M06, by Zhao and Truhlar¹¹ was used with the 6-31+G(d,p) basis set for C, N, O and H. This basis set was used for geometry optimization and energetics of organic molecules during the parametrization of M06. Additionally, this functional has been shown to provide results superior to other general purpose hybrid functionals for medium-sized organic molecules.¹² Numeric integration has been performed with a pruned grid containing 99 radial shells and 590 angular points per shell.

Due to the presence of diradical structures along the reaction pathway, the unrestricted broken symmetry (BS) formulation of M06 was employed. Furthermore, this functional has been recently found particularly suitable for the description of systems with near degenerate states, like diradicals¹³ (a more detailed discussion on the methodological intricacies of diradical wavefunctions can be found in the ESI†). Wavefunction stability was checked for all the computations included in this work. The nature of the stationary points was established by analytical computation of harmonic frequencies. All the calculations were performed with the Gaussian09 package.¹⁴

In order to determine whether orbital control analogous to that of the pericyclic reactions operates in these diradical collapse processes, we computed the stationary points on the potential energy surfaces for both the conrotatory and the disrotatory ring closures of A1, B1 and C1 (see Table 1).

Table 1 Gibbs free activation energies (in kcal mol⁻¹, 298.15 K) and APT charges (in a.u., the charge of bonded H atoms was added into the heavier C atom) computed at the M06/6-31+G(d,p) level of theory for the conrotatory and disrotatory ring closure of A1, B1 and C1

X	Conrotatory		Disrotatory
	ΔG^‡	Charge Cexo	ΔG^‡	Charge Cexo
CH2	8.6	−0.099	13.4	−0.058
NH	12.8	0.058	9.9	0.134
O	22.0	—	7.5	0.413

---

A clear trend can be observed both for the disrotatory and the conrotatory pathways, which is in good agreement with what could be expected from a WH scenario. The disrotatory motion is increasingly more favourable when the collapsing ring structure is more electron rich. On the other hand, the conrotatory motion is the preferred mode of cyclization only for the unpolarized trimethylenemethane vinylogous system A1. Addition of electron withdrawing groups to the cyclizing ring structure destabilizes the conrotation (from 8.6 to 12.8 in B1 and an estimate of 22.0 in C1).

Additionally, APT charges¹⁵ computed at the transition states (see Table 1) also agree with the initial hypothesis of electronegative atoms recruiting electrons for the cyclic structure. The exocyclic methylene, therefore, suffers a charge depletion that runs parallel to the strong 6 π electron behaviour of the forming ring. Values of C–C bond lengths and Mulliken charges for this exocyclic carbon atom also show similar trends consistent with this scheme, although they are less sensitive to the substituents. The bond distances for the exocyclic carbon atom vary from 1.36 Å in both the conrotatory and disrotatory A1 to 1.39 Å in the favoured, disrotatory B1 and C1, suggesting that charge from the bonding π orbital has been withdrawn in the latter and thus displaced towards the forming ring.

Torquoselectivity can be considered an additional orbital selection rule that affects pericyclic ring opening and ring closing reactions. This effect has been most commonly studied in conrotatory systems since they usually feature stronger effects, although disrotatory examples also exist.¹⁶ In order to further explore the degree of orbital control of these diradical reactions, we decided to investigate both directions of conrotation of a series of substituted A1 substrates. We therefore computed the activation energies for the conrotatory ring closure of the bisallylic system A1 featuring electron donating groups (OMe, NH₂, Me) and electron withdrawing groups (CHO, NO₂) with different electronic and steric demands (see Fig. 3). These results are summarized in Table 2.

Fig. 3 Systems considered in the study of torquoselectivity.

Table 2 Gibbs free activation energies (in kcal mol⁻¹, 298.15 K) for the two conrotatory ring closure alternatives of A1_CHO, A1_NO2, A1_Me, A1_NH2 and A1_OMe

X	Conrot. in	Conrot. out	ΔΔG^‡TSin−TSout
	ΔG^‡	ΔG^‡
A1CHO	4.5	8.8	−0.2
A1NO2	4.1	7.3	3.1
A1Me	8.8	8.0	3.7
A1NH2	10.7	5.6	5.3
A1OMe	10.4	6.6	6.6

---

The results collected display an interesting interplay between steric and electronic factors that clearly point towards an orbital model analogue to that proposed by Houk to account for torquoselectivity. Firstly, the conrotatory ring closure of the out isomer shows very small effects upon changes in the electronic demand of the substituents (activation energies being clustered within ∼3.2 kcal mol⁻¹). On the other hand, the in isomers display a strong dependence on the electronic structure of the tuning substituent: electron withdrawing groups stabilize the transition state significantly more compared to electron donors (∼4 vs. ∼10 kcal mol⁻¹). The overall result when comparing ΔΔG^‡_TSin−TSout values is a clear monotonically increasing series of activation energy values with respect to the donating ability of the exocyclic substituent.

Natural Bond Orbital (NBO) analysis¹⁷ also allowed us to locate and diagnose the stabilizing orbital interaction proposed by Houk to explain torquoselective effects in pericyclic reactions. A clear stabilizing charge donation can be found from the bond being formed/broken in the transition state to the low energy empty π* of the acceptor, for both the formyl and the nitro group in the conrotatory ring opening. The energy associated to this charge delocalization within the NBO analysis is 8.4 kcal mol⁻¹ and 13.9 kcal mol⁻¹ for the CHO and NO₂ derivatives, respectively. The natural bond orbitals involved in this interaction for the formyl derivative are illustrated in Fig. 4.

Fig. 4 Bonding and antibonding natural bond orbitals of transition state A2_CHO involved in the charge transfer, analogous to that proposed by Houk to account for torquoselectivity in pericyclic reactions.

In conclusion, these results suggest that the applicability of the Woodward–Hoffmann rules can be extended further, beyond classical pericyclic reactivity. The consequences of orbital control in the diradical ring closing reactions studied here could have great potential if these rules can be generalized and extended, even if only partially, to open shell reactions. Further studies are underway to explore the possible general application of WH rules to an ample set of diradical processes.

Acknowledgements

The Centro de Supercomputación de Galicia (CESGA) is acknowledged for providing a generous allocation of supercomputer time.

Notes and references

1. W. von E. Doering and W. R. Roth, Tetrahedron, 1962, 18, 67.
2. (a) R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395; (b) R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed. Engl., 1969, 8, 781.
3. (a) W. Kirmse, N. G. Rondan and K. N. Houk, J. Am. Chem. Soc., 1984, 106, 7989; (b) W. R. Dolbier, H. Koroniak, D. J. Burton, A. Bailey, G. S. Shaw and S. W. Hansen, J. Am. Chem. Soc., 1984, 106, 1871; (c) C. W. Jefford, G. Bernardinelli, Y. Wang, D. C. Spellmeyer, A. Buda and K. N. Houk, J. Am. Chem. Soc., 1992, 114, 1157.
4. (a) E. R. Davidson, J. J. Gajewski, C. A. Shook and T. Cohen, J. Am. Chem. Soc., 1995, 117, 8495; (b) C. R. W. Guimares, M. Udier-Blagovi and W. L. Jorgensen, J. Am. Chem. Soc., 2005, 127, 3577; (c) C. S. López, O. N. Faza and A. R. de Lera, Org. Lett., 2006, 8, 2055; (d) C. S. López, O. N. Faza and A. R. de Lera, J. Org. Chem., 2009, 74, 2396; (e) O. Gutierrez and D. J. Tantillo, J. Org. Chem., 2012, 77, 8845.
5. (a) O. N. Faza, C. S. López, R. Álvarez and A. R. de Lera, Org. Lett., 2004, 6, 901; (b) D. J. Tantillo, J. Phys. Org. Chem., 2008, 21, 561; (c) D. M. Birney, Curr. Org. Chem., 2010, 14, 1658.
6. (a) J. A. Ross, R. P. Seiders and D. M. Lemal, J. Am. Chem. Soc., 1976, 98, 4325; (b) D. M. Birney, J. Org. Chem., 1996, 61, 243; (c) C. Zhou and D. M. Birney, J. Am. Chem. Soc., 2002, 124, 5231; (d) S. Sharma, T. Rajale, D. B. Cordes, F. Hung-Low and D. M. Birney, J. Am. Chem. Soc., 2013, 135, 14438; (e) C. S. López, O. N. Faza, F. P. Cossio, D. M. York and A. R. de Lera, Chem.–Eur. J., 2005, 11, 1734; (f) C. S. López, O. N. Faza, J. Souto, R. Álvarez and A. R. de Lera, J. Comput. Chem., 2007, 28, 1411.
7. (a) A. Kless, M. Nendel, S. Wilsey and K. N. Houk, J. Am. Chem. Soc., 1999, 121, 4524; (b) J. E. Baldwin, P. A. Leber and D. C. Powers, J. Am. Chem. Soc., 2006, 128, 10020; (c) W. v. E. Doering, T. Zhang and E. K. G. Schmidt, J. Org. Chem., 2006, 71, 5688; (d) C. S. López, O. N. Faza and A. R. de Lera, Chem.–Eur. J., 2007, 13, 5009.
8. C. S. López, O. N. Faza, D. M. York and A. R. de Lera, J. Org. Chem., 2004, 69, 3635.
9. (a) C. S. López, O. N. Faza, K. S. Feldman, M. R. Iyer and D. K. Hester II, J. Am. Chem. Soc., 2007, 129, 7638; (b) K. S. Feldman, M. R. Iyer, C. S. López and O. N. Faza, J. Org. Chem., 2008, 73, 5090; (c) K. S. Feldman, D. K. Hester II, C. S. López and O. N. Faza, Org. Lett., 2008, 10, 1665; (d) K. S. Feldman, D. K. Hester II, M. R. Iyer, P. J. Munson, C. S. López and O. N. Faza, J. Org. Chem., 2009, 74, 4958; (e) O. N. Faza, K. S. Feldman and C. S. López, Curr. Org. Chem., 2010, 14, 1646.
10. (a) P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864; (b) W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133.
11. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
12. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157.
13. Y. Zhao, H. T. Ng, R. Peverati and D. G. Truhlar, J. Chem. Theory Comput., 2012, 8, 2824.
14. M. J.Frisch, et al., Gaussian 09, Rev. A.01, Gaussian, Inc., Wallingford CT, 2004, see ESI† for full citation.
15. J. Cioslowski, J. Am. Chem. Soc., 1989, 111, 8333.
16. (a) S. J. Cristol, R. M. Sequeira and C. H. DePuy, J. Am. Chem. Soc., 1965, 87, 4007; (b) C. H. DePuy, Acc. Chem. Res., 1968, 1, 33; (c) O. N. Faza, C. S. López, R. Álvarez and A. R. de Lera, Org. Lett., 2004, 6, 905; (d) O. N. Faza, C. S. López, R. Álvarez and A. R. de Lera, J. Org. Chem., 2004, 69, 9002.
17. (a) A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899; (b) E. D. Glendening and F. Weinhold, J. Comput. Chem., 1998, 19, 593; (c) F. Weinhold, J. Comput. Chem., 2012, 33, 2363.

---

Footnote

† Electronic supplementary information (ESI) available: Full ref. 14, SCF energies, S² values, Cartesian coordinates and imaginary frequencies for all compounds. Tables with internal energies and enthalpies. HF results and a brief discussion on its performance issues with diradical species. See DOI: 10.1039/c5ra01742d

---