AFM investigation of nanomechanical properties of ZnO nanowires

Abstract

During the investigation of mechanical properties of nanomaterials by atomic force microscope (AFM), a non-normal stress state with large scanning angles is a universal phenomenon. The mechanical service behaviors of ZnO nanowires (NWs) with diameters ranging from 177 to 386 nm under non-normal stress state were studied by AFM at a scanning rate of 14.8 μm s⁻¹. We expanded the application scope of the threshold force equation determining the fracture threshold forces of ZnO NWs which was established in our previous work. The criterion equation for security service of ZnO NWs was established by the threshold force equation and force calibration equation. The criterion equation was used to predict the security service range of ZnO NWs successfully. The modulus and fracture strength of the ZnO NWs were also calculated through the fracture threshold force obtained from the threshold force equation. The results have important and meaningful consequences for security practical applications of ZnO NWs under non-normal stress state.

---

Introduction

One dimensional ZnO nanomaterials are important structural units for fabricating nano-assembly nanodevices and systems owing to their rich morphologies and excellent characteristics. Over the decades, lots of nanodevices based on ZnO nanowires (NWs), nanobelts (NBs), nanorods, and nanoarrays have been fabricated which relied on their remarkable semiconducting, electrical, photoelectric, piezoelectric, electromechanical, chemical stability, biocompatibility, and non-toxic properties. Typical nanodevices include light-emitting diodes, field effect transistors, nanosensors, nanogenerators, and nano-electromechanical systems.^1–9

Nanodevices based on piezoelectric and electromechanical properties need the drive of continuous, periodic external forces or loads, and the efficiencies are related to the size and rate of external forces.^10,11 So the mechanical service behaviors of piezoelectric nanomaterials are important for the practical applications of the corresponding devices. However, most researchers focus on the physical performances of nanodevices at present,^12–18 while few researchers focus on mechanical service behaviors of nanomaterials and nanodevices. Considering that the mechanical properties of nanomaterials allow potential applications of nanostructures in nanodevices, it is important and essential to investigate the mechanical service behaviors of nanomaterials before designing, manufacturing, and operating corresponding nanodevices. Some damage and breakdown phenomena of ZnO NWs or NBs under a mechanical field have been reported in previous work.^19–30 Ni and Boland et al.^19–21 studied the mechanical properties of ZnO NBs and NWs using an atomic force microscope (AFM) nanoindentation or bending method, but it could not supply sufficient forces for breaking down the ZnO NBs or NWs with larger diameters; this was only possible using an expensive diamond tip. Zhu, Xu, and Agrawal et al.^23–27 researched the mechanical properties of ZnO NWs adopting scanning electron microscope (SEM) or transmission electron microscope (TEM) tensile and compressive methods, but the equipment is expensive and the methods are not easy to operate. Any tiny vibrations, external forces or loads would greatly affect the mechanical properties or service behaviors of nanomaterials, while it can be negligible to the macroscopic materials. Bai, Wang, and Zhang et al.^28–30 studied the fatigue properties of ZnO NBs and NWs by in situ TEM electromechanical resonance, which showed excellent fatigue properties. Although it provided cyclical dynamic loads, the method is less effective for studying the mechanical service behaviors of nanomaterials. Although mechanical service behaviors of ZnO NWs have been investigated in recent years, the mechanical service behaviors of ZnO NWs under non-normal stress state studied by AFM are rarely reported. Actually, in most instances, ZnO NWs as the structural units damaged or fractured in nanodevices under non-normal stress state are a commonly encountered mode that determines the stability and lifetime of the nanodevices.

In this paper, the mechanical service behaviors of ZnO NWs under non-normal stress state were studied by AFM at a scanning rate of 14.8 μm s⁻¹. The scope of the force calibration equation determining the actual forces applied on the ZnO NWs established in our previous work was expanded. The criterion for security service of ZnO NWs was established by the threshold force equation and force calibration equation to predict the mechanical service behaviors of ZnO NWs under non-normal stress state. The modulus and fracture strength of the ZnO NWs were also calculated through the fracture force obtained from the threshold force equation.

Experimental section

ZnO NWs used in our experiments were synthesized by chemical vapor deposition (CVD).³¹ Equimolar ZnO and reductive carbon powders were mixed and used as the zinc source. The mixture was added to the aluminium ceramic boat, then a silicon substrate covered with about 20 nm Au film was placed on top and the positive face was pointed to the mixture. The vertical distance between the mixture and the silicon substrate was about 1–2 mm. The ceramic boat was inserted into a quartz tube furnace under a constant flow of argon and oxygen. The flow rate was controlled between 50–80 standard cubic centimeters per minute, and the proportion of oxygen was 2–5%. The ceramic boat was heated to 920–980 °C for 15–20 min, and cooled in the air. The morphology of ZnO NWs was observed in SEM (FEI, Quanta 3D FEG), the lattice spacing and growth direction were observed by TEM (FEI, Tecnai F30).

Then, the mechanical service behaviors of ZnO NWs were studied by AFM (Bruker, Multimode III) in the scanning process with large scanning angles (the angles between the ZnO NW length direction and AFM tip moving direction) at a rate of 14.8 μm s⁻¹. The experimental procedures were carried out as follows. Firstly, ZnO NWs were ultrasonicated in ethanol, and dispersed on insulating silicon distributed with trench arrays. Secondly, ZnO NWs were double-fixed by Pt lines at both ends on the trenches through focused ion beam (FIB) deposition. Finally, AFM three-point bending was used for applying forces to measure the modulus and threshold forces of the fixed ZnO NWs.

Results and discussion

The SEM images of ZnO NWs used in our experiments are shown in Fig. 1a. The diameters of the ZnO NWs are distributed between tens to hundreds of nanometers. From the inset in Fig. 1a, it can be seen that the surfaces of the ZnO NWs are smooth. The high-resolution TEM (HRTEM) image and selected area electron diffraction (SAED) pattern are shown in Fig. 1b, which indicate that the ZnO NW is single crystal and grows along the [0001] direction. A schematic representation of AFM for applying forces in the scanning process on the fixed ZnO NW is shown in Fig. 1c. The scanning direction was parallel to the trenches, so a large scanning angle was formed between the direction of the length of the fixed ZnO NW and the scanning direction.

Fig. 1 (a) SEM images of ZnO NWs (inset: high magnification SEM image of the ZnO NWs). (b) HRTEM and corresponding SAED pattern of a single ZnO NW. (c) Schematic of AFM for probing of mechanical service behaviour of the fixed ZnO NW with large scanning angles.

Application scope expansion of threshold force equation

According to the schematic in Fig. 1c, the mechanical service behaviors of ZnO NWs under a non-normal stress state with large scanning angles were investigated in the scanning process of AFM tip at a scanning rate of 14.8 μm s⁻¹. External forces were increased gradually from 0 nN until the ZnO NW fractured. Fig. 2a and d show SEM images of two ZnO NWs with diameters of 187 nm and 348 nm in the experiments, respectively. Fig. 2b,c and e,f show AFM images of the above two ZnO NWs before the test and after fracture, respectively. Diameters of the ZnO NWs, scanning angles, and fracture forces are shown in Table 1. The relationship between the fracture forces and diameters of ZnO NWs is shown with green points and fitted line in Fig. 2g.

Fig. 2 (a and d) SEM images of two ZnO NWs with diameters of about 187 and 348 nm. AFM images of the ZnO NWs with scanning angles of (b and c) 50° and (e and f) 76° before the test and after fracture under the applied forces. (g) Relationship between the fracture force F, threshold forces F_th and diameters of ZnO NWs. (h) Coincidence of the threshold forces of the ZnO NWs calculated by threshold force equation and force calibration equation, and the light blue triangle is the security zone.

Table 1 The geometrical and mechanical parameters of the ZnO NWs under forces applied by AFM with large scanning angles

No.	D (nm)	Ff (nN)	Fth (nN)	θ (°)	μ2	μ2 sin θ	β	Fth-l (nN)
1	177	812.5	2219.7	84	2.5	2.49	2.68	2177.42
2	187	1062.5	2386.9	50	2.68	2.05	2.28	2140.88
3	193	937.5	2487.22	64	2.54	2.28	2.49	2336.53
4	219	1312.5	2921.94	51	2.66	2.07	2.3	3014.03
5	223	1437.5	2988.82	41	2.98	1.96	2.2	2882.25
6	254	1562.5	3507.14	40	3.04	1.95	2.2	3429.84
7	296	1687.5	4209.38	68	2.53	2.35	2.55	4303.29
8	301	1937.5	4292.98	42	2.93	1.96	2.2	4264.24
9	348	2062.5	5078.82	76	2.51	2.44	2.63	5100.86
10	386	2187.5	5714.18	76	2.51	2.44	2.63	5759.03
11	318	1937.5	4577.22	76	2.51	2.44	2.63	5095.63
12	403	—	5998.42	4	27.88	1.94	2.18	—

---

According to the threshold force eqn (3) (F_th = 16.72d–739.74, range of application: 67 nm ≤ d ≤ 201 nm. This equation describes the relationship between fracture threshold forces of ZnO NWs and their diameters when the scanning angle is smaller than 3°, and in this situation the external forces leading to the fracture of ZnO NWs can be seen as the fracture threshold forces; when the scanning angle is larger than 3°, the actual forces applied on the ZnO NWs should be calibrated by a calibration coefficient β by multiplying the external forces. A detailed introduction can be found in our previous article ref. 32) of fracture threshold forces F_th and diameters of ZnO NWs established in our previous work,³² the fracture threshold forces F_th can be also obtained and shown with red points in Fig. 2g and h.

In order to verify the extendability of the scope of the threshold force equation, the calibrated fracture threshold forces F_th-l (F_th-l can be calculated from the force calibration equation F_th-l = βF_f, when the scanning angle is larger than 3°.³² β = [1 + (μ₂ sin θ)²]^1/2: calibration coefficient, μ₂: lateral resistance friction coefficient, θ: scanning angle, the values measured are shown in Table 1.) are also calculated and shown with purple points in Fig. 2h.

It can be seen that the two sets of fracture threshold force values (calculated by threshold force equation and force calibration equation, respectively) have good coincidence and present a good linearity with diameters of the ZnO NWs which indicates that the threshold force equation can be applied to a wider size range. The calculated threshold force values are also shown in Table 1.

Establishment of criterion equation for security service of single ZnO NWs

In addition, the criterion equation predicting the security service range of ZnO NWs can be obtained by the cooperation of threshold force equation and force calibration equation. The evaluation equation can be written as the flowing two forms:

βF = F_r−l < F_th = 16.72d − 739.74 (1)

βF = F_r−l ≥ F_th = 16.72d − 739.74 (2)

Eqn (1) is the security criterion equation, and eqn (2) is the damage or fracture criterion equation. If the actual force F_r−l applied on the ZnO NW is smaller than the fracture threshold force F_th, the ZnO NW can work safely; while the actual force F_r−l applied on the ZnO NW is larger than the fracture threshold force F_th, the ZnO NW would fracture.

Then, the criterion equation was used to predict the security of two ZnO NWs with diameters of 318 nm and 403 nm under some certain forces F that are shown in Fig. 3, and the calculated values are shown in Table 1 of no.11 and 12. The fracture threshold force F_th of the 318 nm ZnO NW calculated by threshold force equation was 4577.22 nN. The experimental applied force F leading the ZnO NW breakdown was 1937.5 nN, and it can provide the actual force F_r−l of 5095.63 nN (2.63 × 1937.5). So the experimental data are in accordance with the damage or fracture criterion eqn (2) (Fig. 3a–c). For the 403 nm ZnO NW, the largest applied force F the AFM tip can provide was 2687.5 nN, and the largest actual force F_r−l was 5858.75 nN (2.18 × 2687.5). However, the calculated fracture threshold force F_th led the ZnO NW fracture was 5998.42 nN (16.72 × 403–739.74). Since the calculated results meet the security criterion equation, the ZnO NW would not fracture under the applied force (Fig. 3d–f). The experimental results are consistent with the criterion equation which further certify the credibility of the criterion equation. The security zone is shaded light blue below the experimental data in Fig. 2h.

Fig. 3 (a) SEM images of one single ZnO NW with diameters of about 318 nm. AFM (top) and 3D AFM (bottom) images of the ZnO NWs with 76° (b) before test and (c) after applying the force marked in the image. (d) SEM images of one single ZnO NW with diameters of about 403 nm. AFM (top) and 3D AFM (bottom) images of the ZnO NWs with 4° (e) before test and (f) after applying the force marked in the image.

Young’s modulus and fracture strength of single ZnO NW

The mechanical properties of a single ZnO NW can be well described by the mechanical model described previously that accounts for bending. The equation^19,33,34 is as follows: where E is the Young’s modulus of the ZnO NW, Δz is the resulting displacement of the NW under the effect of the applied force, I = πR⁴/4 is the moment of inertia for a cylindrical wire, L is the length of the NW, f(α) is defined as follows:where α is related to the displacement Δz of the ZnO NW by

Fig. 4a shows the Young’s modulus (the data also include a part obtained in ref. 32) of the ZnO NWs. It can be seen that the Young’s modulus of ZnO NWs exponentially decreased with an increase of diameter. It is surprising that the Young’s modulus values of ZnO NWs with larger diameters are far below the values in ref. 20, which indicates that the ZnO NWs with larger diameters have more defects.

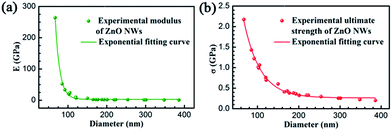Fig. 4 Relationship between (a) Young’s modulus, (b) fracture strength of ZnO NWs and diameters obtained in the experiments.

The fracture strength (the data also include a part obtained in ref. 32) of the ZnO NW can be calculated using the following equation:³⁵

where

The fracture strength curve of the ZnO NW is shown in Fig. 4b. It can be seen that the fracture strength of ZnO NWs also exponentially decreased with an increase of diameter. The fracture strength values are approaching the values of ZnO NWs in ref. 17 and the values of bulk ZnO especially when the diameters exceed 200 nm.³⁶ The calculated results indicate that the defects would greatly reduce the Young’s modulus of ZnO NWs, but have few effects on the fracture strength.

In practical applications, the nanomaterials building for the devices is inevitably influenced by external conditions, such as slight vibration and noise which are negligible for macroscopic devices, so the results obtained in the scanning process under non-normal stress state are more valuable for designing, fabricating, and operating electromechanical and piezoelectric nanodevices.

Conclusions

In summary, the mechanical service behaviors of ZnO NWs with diameters ranging from 177 to 386 nm under non-normal stress state with large scanning angles were studied by AFM at a scanning rate of 14.8 μm s⁻¹. The application scope of threshold force equation determining the threshold forces of ZnO NWs was expanded to larger diameter of ∼400 nm. The criterion for security service of ZnO NWs was established by the combination of threshold force equation and force calibration equation. The criterion was used to predict the security service range of ZnO NWs successfully. The Young’s modulus of the ZnO NWs obtained in the scanning process is far below the values measured under a static state in a previous report, but the fracture strength has good consistency. The results have important and meaningful consequences for practical applications of ZnO NWs under non-normal stress state.

Acknowledgements

This work was supported by the National Major Research Program of China (2013CB932602), the Major Project of International Cooperation and Exchanges (2012DFA50990), the Program of Introducing Talents of Discipline to Universities (B1400), NSFC (51232001, 51172022, 51372023, 51372020), the Fundamental Research Funds for the Central Universities, the Program for Changjiang Scholars and Innovative Research Team in University. The New Century Excellent Talent of Ministry of Education (NCET-12-0777).

Notes and references

1. Z. L. Wang and J. H. Song, Science, 2006, 312, 242–246.
2. Q. L. Liao, Z. Zhang, X. H. Zhang, M. Mohr, Y. Zhang and H. J. Fecht, Nano Res., 2014, 7, 917–928.
3. X. D. Wang, C. J. Summers and Z. L. Wang, Nano Lett., 2004, 4, 423–426.
4. X. M. Zhang, M. Y. Lu, Y. Zhang, L. J. Chen and Z. L. Wang, Adv. Mater., 2009, 21, 2767–2770.
5. Y. K. Chang and F. C. Hong, Nanotechnology, 2009, 20, 235202.
6. P. Lin, X. Chen, X. Q. Yan, Z. Zhang, H. G. Yuan, P. F. Li, Y. G. Zhao and Y. Zhang, Nano Res., 2014, 7, 860–868.
7. Y. W. Heo, L. C. Tien, Y. Kwon, D. P. Norton, S. J. Pearton, B. S. Kang and F. Ren, Appl. Phys. Lett., 2004, 85, 2274.
8. Z. Zhang, Q. L. Liao, X. H. Zhang, G. J. Zhang, P. F. Li, S. N. Lu, S. Liu and Y. Zhang, Nanoscale, 2015, 7, 1796–1801.
9. Y. Yang, W. Guo, X. Q. Wang, Z. Z. Wang, J. J. Qi and Y. Zhang, Nano Lett., 2012, 12, 1919–1922.
10. R. S. Yang, Y. Qin, L. M. Dai and Z. L. Wang, Nat. Nanotechnol., 2009, 4, 34–39.
11. J. H. Song, H. Z. Xie, W. Z. Wu, V. R. Joseph, C. F. Wu and Z. L. Wang, Nano Res., 2010, 3, 613–619.
12. J. Xiang, W. Lu, Y. J. Hu, Y. Wu, H. Yan and C. M. Lieber, Nature, 2006, 441, 489–493.
13. B. Z. Tian, T. Cohen, Q. Qing, X. J. Duan, P. Xie and C. M. Lieber, Science, 2010, 329, 830–834.
14. H. Yan, H. S. Choe, S. W. Nam, Y. J. Hu, S. Das, J. F. Klemic, J. C. Ellenbogen and C. M. Lieber, Nature, 2011, 470, 240–244.
15. Z. Z. Wang, J. J. Qi, S. N. Lu, P. F. Li, X. Li and Y. Zhang, Appl. Phys. Lett., 2013, 103, 143125.
16. M. J. Lee, S. W. Han, S. H. Jeon, B. H. Park, B. S. Kang and S. E. Ahn, Nano Lett., 2009, 9, 1476–1481.
17. S. N. Lu, J. J. Qi, S. Liu, Z. Zhang, Z. Z. Wang, P. Lin, Q. L. Liao, Q. J. Liang and Y. Zhang, ACS Appl. Mater. Interfaces, 2014, 6, 14116–14122.
18. R. Zhu and R. S. Yang, Nanotechnology, 2014, 25, 345702.
19. H. Ni and X. D. Li, Nanotechnology, 2006, 17, 3591–3597.
20. B. M. Wen, J. E. Sader and J. J. Boland, Phys. Rev. Lett., 2008, 101, 175502.
21. G. Y. Jing, X. Z. Zhang and D. P. Yu, Appl. Phys. A, 2010, 100, 473–478.
22. Y. Zhang, X. Q. Yan, Y. Yang, Y. H. Huang, Q. L. Liao and J. J. Qi, Adv. Mater., 2012, 24, 4647–4655.
23. Q. Chen and J. Zhu, Appl. Phys. Lett., 2007, 90, 043105.
24. S. Hoffmann, F. Ostlund, J. Michler, H. J. Fan, M. Zacharias and S. H. Ballif, Nanotechnology, 2007, 18, 205503.
25. F. Xu, Q. Q. Qin, A. Mishra, Y. Gu and Y. Zhu, Nano Res., 2010, 3, 271–280.
26. R. Agrawal, B. Peng, E. E. Gdoutos and H. D. Espinosa, Nano Lett., 2008, 8, 3668–3674.
27. R. Agrawal, B. Peng and H. D. Espinosa, Nano Lett., 2009, 9, 4177–4183.
28. X. D. Bai, P. X. Gao and Z. L. Wang, Appl. Phys. Lett., 2003, 82, 4806–4808.
29. Z. Y. Gao, Y. Ding, S. S. Lin, Y. Hao and Z. L. Wang, Phys. Status Solidi RRL, 2009, 3, 260–262.
30. P. F. Li, Q. L. Liao, S. Z. Yang, X. D. Bai, Y. H. Huang, X. Q. Yan, Z. Zhang, S. Liu, P. Lin, Z. Kang and Y. Zhang, Nano Lett., 2014, 14, 480–485.
31. P. F. Li, Q. L. Liao, Z. Zhang, Z. Z. Wang, P. Lin, X. H. Zhang, Z. Kang, Y. H. Huang, Y. S. Gu, X. Q. Yan and Y. Zhang, ACS Appl. Mater. Interfaces, 2014, 6, 2344–2349.
32. P. F. Li, Q. L. Liao, Z. Z. Wang, P. Lin, Z. Zhang, X. Q. Yan and Y. Zhang, RSC Adv. submitted.
33. L. D. Landau and E. M. Lifshitz, Theory of elasticity, Pergamon, Oxford, 1970.
34. A. Heidelberg, L. T. Ngo, B. Wu, M. A. Phillips, S. Sharma, T. I. Kamins, J. E. Sader and J. J. Boland, Nano Lett., 2006, 6, 1101–1106.
35. J. M. Gere and S. P. Timoshenko, Mechanics of materials, PWS-KENT, Boston, MA, 1990.
36. C. S. Lu, R. Danzer and F. D. Fischer, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 067102.

---