Effects of thermal rippling on the frictional properties of free-standing graphene†
Abstract
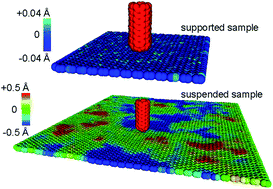
With the use of simulated friction force microscopy, we present the first study of the effect of varying temperature on the frictional properties of suspended graphene. In contrast with the theory of thermally activated friction on the dry surfaces of three-dimensional materials, kinetic friction is demonstrated to both locally increase and decrease with increasing temperature, depending on sample size, scanning tip diameter, scanning rate, and the externally applied normal load. We attribute the observed effects to the thermally excited flexural ripples intrinsically present in graphene, demonstrating a unique case of temperature-dependent dynamic roughness in atomically thin layers. Consequently, our results suggest strain-induced control of friction in nanoelectromechanical systems involving free-standing regions of atomically thin membranes.

 Please wait while we load your content...
Please wait while we load your content...