Relation between molecular structure of smectite and liquefaction of mudstone
Guichen Li,
Zuohan Jiang,
Xiaowei Feng*,
Nong Zhang and
Xingliang Xu
Key Laboratory of Deep Coal Resource Mining, Ministry of Education of China, China University of Mining and Technology, Xuzhou, Jiangsu 221116, PR China. E-mail: fxw_mining@foxmail.com; Tel: +86-18796246921
First published on 24th February 2015
Abstract
The elements and microstructure of typical mudstone were analysed by X-ray diffraction and scanning electron microscopy. The mudstone was composed mainly of clay minerals, with granules that form clumps with a ‘fluffy’ appearance. Pores in the clumps provide channels for water penetration. Materials Studio (MS) software was applied to simulate a double unit cell structure model of smectite. We then simulated the hydration process of smectite, demonstrating that single, double, and triple layers of saturated water molecules can be inserted within the cell structure with 48, 128 and 224 adsorbed water molecules, respectively. We also studied the microscopic structural change of smectite-dominated mudstone under different degrees of water soaking, and found that an energy exchange occurs between the water molecules and skeleton molecules of the smectite. This leads to a weakening of the intermolecular forces of smectite, which reduces the bonding among the clay minerals. Thus, this process directly leads to the breakage of the smectite microstructure: the granules detach from the surface and the fissures expand, resulting in mudstone with macroscopic phenomena such as argillization and liquefaction.
1 Introduction
Mudstone is widely distributed in our planet. In underground engineering projects, especially in deeply buried coal mine roadways, mudstone can cause severe instability. As mudstone interacts readily with water, it is common to encounter softening and argillization of the mudstone. The surrounding rock mass may be rapidly isolated and softened under the combined influence of water penetrating through the fissures and mining-induced pressure, resulting in rock failure such as roof convergence, floor movement and deformation of the roadway walls. Thus, with recurrent geological alteration, roadways will undergo repeated repairs and breakage phases,1 disrupting the normal excavation and mining operation and causing a safety hazard in the mine.The rheological properties of a rock are affected by both time and the stress–strain relation of the rock mass, and involve creep deformation, stress relaxation, and elastic aftereffect.2 Current studies on the rheological properties of mudstone focus mainly on typical physicochemical properties, especially on the aspects of the swelling of clay minerals and the microstructure of mudstone.
Studies on the relationship between the mineral constituents and physical–mechanical properties of soft rock include that of Chen who investigated the swelling effects of mudstone caused by dilatation.3 These effects can occur as a result of breakage expansion, free expansion by physicochemical interaction, and rheological expansion caused by elastic deformation. Qu et al.4 and Xia5 examined the properties of mudstone, taking into account the combined effects of mineral composition, dilatation, and physicochemical expansion. Peng et al.6 and Zhou et al.7 analysed the mechanical properties of soft rocks under different mineral and moisture contents. Ma et al.8 showed that the stress states and corresponding curves vary if the clay mineral in the mudstone is subjected to high stress or low stress.
From the perspective of microstructure, temporal changes in the structural liquefaction and mechanical response of the rock will occur on a structural plane based on its stress state, which will result in a distinctive liquefaction of the engineering rock mass. The microstructure of soft rock under a saturated state was analysed by Tan,9 who showed that the main reason for the mechanical property deterioration lies in the comprehensive effects of the multiple mechanisms of Scanning Electron Microscopy (SEM). Huang10 focused on the microstructure evolution of kaolinite at a saturated state and showed that softening and disintegration can occur while the content of illite and kaolinite is sufficiently high, even without smectite. Zhang11 analysed the relationship between the microscopic structure and macroscopic mechanical properties of mudstone under high temperature using X-Ray Diffraction (XRD) and SEM. Although these studies provide much detail on the properties of mudstone and the softening processes, the main constituents and especially the inner molecular structure of the mudstone have not been examined in detail.
2 Microstructure tests on natural mudstone
2.1 X-ray diffraction analysis
The Liuhai colliery is located in the Longkou district of Shandong Province, where the geology is of classic tertiary soft rock. The diagenesis time of this sedimentary strata is relatively short, and the rock mass is characterised by poor cementing properties and low strength. The rock in the immediate roof and immediate floor of coal seam no. 1 is loose and soft because of the high content of expansile clay minerals such as smectite and illite, which account for more than 90% of the rock mass. Thus, the rock in the study area is easily weathered and dilated. Furthermore, the geologic structure in this colliery is complex and joints are widely distributed in the rock mass. Hence, the rock mass is fractured and has low strength; the average strength being 1–2 MPa.The samples were randomly drilled from the mudstone columns of the roof and floor of coal seam no. 1. Breakage phenomena such as argillization and liquefaction are extensive in these columns, and the specimens were sealed up immediately to prevent weathering during transport. The specimens were prepared according to the Petroleum Industrial Standards No. SY/T5163-1995. The diffraction experiment was conducted using a D/Max-3B X-ray diffraction instrument (made by Rigaku, a Japanese corporation), and the clay mineral determination and related quantitative analysis based on a comparison of the diffraction peak intensity were conducted according to the Petroleum Industrial Standard. The results (Table 1 and Fig. 1) show that this type of clay mineral is mainly composed of smectite (over 70%), followed by illite, kaolinite, chlorite and trace amounts of quartz, feldspar and others. This indicates that the tested mudstone is smectite.
| Specimen ID | Specimen drilling site | I | I/S | S | Cl | K |
|---|---|---|---|---|---|---|
| a Notes: S-smectite, I-illite, I/S-compound of smectite and illite, K-kaolinite, CL-chlorite, Q-quartz, F-feldspar (analysis results on the specimens taken from immediate roof and floor of coal seam no. 1 of the Liuhai mine). | ||||||
| 1 | Immediate floor of coal seam no. 1 | 7 | 9 | 76 | 2 | 6 |
| 2 | Immediate roof of coal seam no. 1 | 14 | 4 | 72 | 3 | 7 |
2.2 Analysis of SEM results
The natural mudstone was crushed, dyed, and dehydrated for observation by SEM. The microstructure images of the natural mudstone obtained by SEM are shown in Fig. 2. The images of magnification ×1000 show that the mudstone has a relatively high clay mineral content, which is concentrated in clumps arranged in a crisscross pattern. The overall structure has a ‘fluffy’ appearance, with pores distributed randomly. Coarse granules, such as quartz and mica, are distributed among the clay minerals. The ×3000 magnification shows a different view: the clay minerals are not completely bonded together and many small gaps divide them into random clumps. | ||
| Fig. 2 Scanning electron microscopy images of natural mudstone, (a) magnification ×1000, (b) magnification ×3000. | ||
The XRD results and SEM images demonstrate that the smectite group of minerals are a dominant component of the mudstone. The mineral appears in clumps with scattered quartz and mica granules. The relatively weak bonding ability between the smectites results in large numbers of pores surrounding the minerals. These pores provide numerous tiny passages for water to seep into. Therefore, the overall performance of mudstone is strongly affected by the mineral properties and microstructure of the clay minerals.
3 Argillization simulation of smectite-dominated mudstone
3.1 Brief introduction to the Materials Studio software
The software package Materials Studio (MS) was initially developed by Accelrys Corporation of America and designed for researchers in material science.12 It is capable of conducting X-ray diffraction analysis, configuration optimization, property prediction, and complex dynamic simulation or quantum mechanics. Additionally, a flexible Client–Server structure and multi-functional modules are fully equipped to build molecules, optimize structure and perform numerical simulation. The kernel module is Materials Visualizer, which provides all the necessary tools to construct molecules, crystals and high polymer materials.To intuitively display the hydration process of a clay mineral on a molecular level, molecular modelling and molecular simulation were introduced to simulate the activity of the molecular aggregations of the clay mineral, from which the macroscopic properties of the molecular system could be calculated. Simulation research on the molecules within the layered structure of smectite can present a quantitative model of embedded relationships and has been widely applied in various studies on the structure of smectite. By using the Monte Carlo method and molecular dynamics theory, de Pablo et al.13 and Tao et al.14 studied the influence of K+, Na+ and Ca2+ on the stability and expansibility of the smectite model. Zheng and Zaoui15 examined the diffusion properties of water molecules and ions in Wyoming-type smectite structure containing single, double, and triple layers of water molecules by using the molecular dynamics theory. Guerra et al.16 showed that the adsorption property of clay depends mainly on the pH value, contact duration and initial concentration of the adsorption ions in the adsorptive solution. Mignon et al.17 carried out molecular simulation to study the hydration properties of different types of smectite (Li+-, Na+- and K+-type). Their results show that the expansion and hydration properties of these three types of smectites depend mainly on the water affinity of the positive ions between the smectite layers and on the degree that these positive ions control the negative charges on the surface of the oxygen atoms. Liu and Chen18 and Ebrahimi et al.19 used the updated Clayff mechanic model in the MS software to study the nanoscale elastic properties of the interlayer water systems in clay minerals and the function of the interlayer spacing in a smectite model. Hensen and Smit,20 Aggarwal21 and Nakano et al.22 also carried out research on the adsorption properties of water molecules on the surface of clay minerals and the properties of the interlayer water molecules in clay minerals using different molecule simulation methods. In this paper, we used MS to construct the molecular structure of smectite, noting that the smectite is the main component of the tested mudstone. We examined microcosmic structural images of mudstone under different degrees of soaking and analysed the relationship between the water adsorption ability of smectite, microcosmic structural change, and microscopic argillization liquefaction.
3.2 Simulation, results and discussion
The MS double unit cell model of smectite has a space group 12C2/m and a symmetry class L2PC. The cell units were built by inputting the parameters α, β, γ, a, b and c, where α = γ = 90°, β = 99°, a = 5.23, b = 9.06, and c varies with the number of water molecules and the exchangeable positive ions among the layers.23 Taking into account restrictions such as the spacing between the crystal layers, the electric charges in the system, and the van der Waals force, the double unit cell model in this study comprised 4a × 2b × 2c unit cells and the space group was P1.24 The lattice replacement of aluminium ions and silicon ions was carried out in an alumina octahedral network and silica tetrahedral network, respectively. Based on the ideal structure of smectite, one aluminium ion of every eight was replaced by a magnesium ion in the octahedral unit cell, while one silica ion of every thirty-two was replaced by an aluminium ion.25 This process simultaneously produces negative charges in the layers of crystal polyhedrons and introduces positive ions such as Na+, K+, Ca2+ and Mg2+ into the layers so as to reach a charge balance. Normally, a certain number of positive ions act as compensation ions, so more than one type of positive ion exists in the layers of a typical smectite. It is reasonable to assume that the various sizes and charges of these interlayer positive ions would affect the hydration properties of smectite differently. Li+-dominated smectite is more likely to undergo hydration, followed by Na+ and then K+.26 For simplicity, the intermediate Na+-dominated smectite was chosen for our analysis.The double unit cell structure in this simulation comprises 16 singular unit cells, with 8 aluminium ions being replaced by magnesium ions in the octahedral unit cell and 4 silica ions being replaced by aluminium ions in the tetrahedral unit cell. The replacements are symmetrically distributed within the polyhedral structure. Twelve intra-layer sodium ions are compensated to balance the charges. The chemical formula of the model is NaAl3MgSi8O20(OH)4, and its reaction with water can be expressed as:
| NaAl3MgSi8O20(OH)4 + nH2O → NaAl3MgSi8O20(OH)4·nH2O. |
Three-dimensional boundary conditions are applied in the crystal simulation; the macroscopic system is unlimited and repeatedly simulated in all three dimensions. Finally, a double unit cell structure of smectite is formed as shown in Fig. 3.
Universal Force Field (UFF) is applied in this study, this field was initially accomplished by Rappe and his cooperators in 1992, it thus owns an extensive application scope, and it is applicative for all elements in periodic table of elements. It also can be adopted to conduct simulated calculation on smectite–water–ion system.
Simulated system belongs to periodic system, and Ewald summation method is utilized to calculate long-range electrostatic interactions. The real space cutoff is set as 9.0 Å and the reciprocal space cutoff is set as 0.5–1 Å.
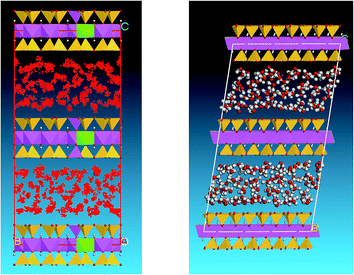
The H2O molecules were built in another window, and charges and a force field were attached to them. Additionally, the configuration of the water molecules was optimized to avoid spallation of the smectite structural system when external particles were introduced to the system. The sorption module of MS was then used to assist the incorporation of the water molecules into the optimized smectite structure system. The default temperature, pressure, and relative humidity were 298 K, 105 Pa, and 75%, respectively. The water molecules were added gradually. For c = 12.5 Å, after the 48th molecule was added, the software warned that no more molecules could be added. This was also the point where the first layer of saturated water molecules formed, as displayed in Fig. 4. Fig. 4 indicates that the 48 water molecules are divided into two parts; they are separately adsorbed by the Na+ ions and distributed around them. The Na+ ions lie between the crystal layers of smectite, and the molecular structure of the smectite is not affected at all.
Na et al.27 and Chang and Skipper28 showed that as single, double, and triple layers of water molecules are adsorbed by the smectite structure in the model, this is equivalent to adsorption of 0.1 kg, 0.2 kg and 0.3 kg of water per 1 kg of smectite, respectively. After measuring the smectite content in the mudstone, we conducted a soaking experiment on the mudstone; the soaking duration and the weight difference before and after soaking were precisely controlled. Then, mudstone specimens representing the approximate water molecules adsorption states of single, double, and triple layers, were selected and observed by SEM (Fig. 5).
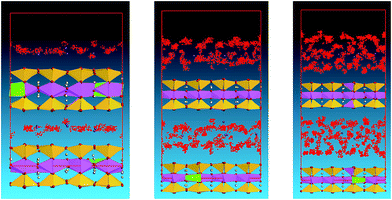
Subtle changes in the microstructure of the mudstone can be observed as the smectite is soaked in water for different levels (Fig. 5). The bonding strength between the granules is decreased and many course granules are detached; the pores are filled with water, and some expand and merge into larger pores. This process is also accompanied by the formation of fissures, which split newly developed clumps into smaller ones. These processes lead to enlargement of the total surface area of the cell structure, which increases the contact area for clay mineral and water interaction, thus enhancing mudstone hydration.
As the water adsorption of smectite increases, the interval between the layers also increases. In the model, the growth of the inter-layer space can be represented by adjusting the value of c, whereby more water molecules can be inserted. For the case of c = 15.5 Å, once 128 molecules were merged into the structure, the software warned that no more water molecules could be added. Under these conditions, double layers of saturated water molecules were formed, as shown in Fig. 6. Compared with the structure of a single layer of water molecules, the smectite structure in this case did not change. The water molecules are randomly distributed between the crystal layers, but an overall indistinct double-layer distribution can be observed.
Fig. 7 shows the microstructure of a mudstone sample which adsorbed double layers of water molecules. The bonding between the granules is further reduced because of the higher water adsorption content, coarse grains such as quartz and mica are detached from the main structure, and laminar structures of clay mineral are clearly visible. Additionally, many pores appear, creating direct contact between neighbouring microstructures. This decreases the anti-shear capability of the mudstone and increases the possibility of sliding breakage occurring under exogenic forces.
When c, the interval between the layers, was 18.5 Å, the numerical processing was terminated after 224 water molecules had been added. At this point, triple layers of saturated water molecules were formed, as shown in Fig. 8.
Fig. 9 shows the microstructure of a mudstone sample with triple layers of adsorbed water molecules. The granules are loosely distributed, with many pores and fissures joined together, forming large and distinctive fissures. In this state, the microstructure of mudstone is quite loose and porous. The whole procedure will transfer the mudstone from its initial highly bonded state and relatively strong structure into a weak state with crisscrossed fissures distributed throughout its structure.
The microstructure analysis of the hydration simulation of smectite-dominated mudstone with different levels of soaking shows that single, double, and triple layers of water molecules can be sequentially added between double unit cells of smectite with 48, 128 and 224 adsorbed water molecules, respectively. The hydration process of the mudstone leads to microstructure breakage, as shown in Fig. 10, where the bonding strength between the granules is reduced and large fissures gradually develop. These fissures cause internal asymmetry which concentrates the stress and further isolates elements of the structural system of the mudstone, resulting in distinctive macroscopic phenomena such as argillization and rheological behavior.29
 | ||
| Fig. 10 Fissure development and macroscopic appearance of argillization of smectite-dominated mudstone. | ||
4 Energy optimization in smectite structure
4.1 Structure variation after energy optimization
We selected structural systems that contained single, double, and triple layers of saturated water molecules; these were formed from the original smectite double unit cell structure by adsorption of 48, 128 and 224 water molecules. The Geometry Optimization – Smart algorithm in the Forcite module was adopted to perform structural optimization on the model, with a Universal force field. In addition, rigid restrictions on the polyhedron were also applied to ensure the stability of the model while allowing ions to move freely between the layers. The simulation results are displayed in Fig. 11. Comparing the structures of the optimized and non-optimized models, we see that when the system was not optimized, the silica tetrahedron and alumina octahedron within the system retained their regular shape and smooth pattern, and the water molecules were evenly distributed among the crystal layers. However, when the system was optimized, silica tetrahedron and alumina octahedron structures were altered, becoming irregular polyhedrons, with water molecules irregularly diffused among the crystal layers. Furthermore, the interlayer Na+ ions showed a clear tendency to occupy the surface of the silica tetrahedron because of the restricting conditions on the model which dictate that the model cannot dilate spontaneously with the ongoing process of hydration. This caused the initial upper layer of the smectite molecular layer to disappear.4.2 Energy parameters before and after optimization of the smectite model
Table 2 was derived by analysing the changes in the energy parameters of the smectite structural model before and after the optimization.| Number of water molecules | Optimizing duration | Chemical-bond energy (kcal mol−1) | Non-bond energy (kcal mol−1) | Total energy (kcal mol−1) | |||
|---|---|---|---|---|---|---|---|
| Bonds | Angles | Torsions | van der Waals | Electrostatic | |||
| 48 | Before | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 967.828 967.828 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 473.474 473.474 |
35.454 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 721 721![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 172.587 172.587 |
6050.029 | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 796 796![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 699.372 699.372 |
| 48 | After | 7346.036 | 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 878.222 878.222 |
50.378 | 1216.532 | −73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 477.311 477.311 |
−23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 986.143 986.143 |
| 128 | Before | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798.225 798.225 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800.046 800.046 |
35.454 | 2.87121 × 108 | −224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 947.887 947.887 |
2.86968 × 108 |
| 128 | After | 1524.215 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160.753 160.753 |
43.317 | 1251.327 | −249![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919.499 919.499 |
−209![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 939.887 939.887 |
| 224 | Before | 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 798.199 798.199 |
48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800.045 800.045 |
35.454 | 3.13752 × 108 | −224![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 431.946 431.946 |
3.1359 × 108 |
| 224 | After | 1503.314 | 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 215.408 215.408 |
41.772 | 1274.964 | −250![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 026.383 026.383 |
−209![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 990.924 990.924 |
Table 2 shows that the total energy of the system is significantly decreased after energy optimization on the double unit cell crystal of the smectite model. Among the energy sources, the van der Waals force shows the most dramatic decrease, indicating that when the intermolecular forces that initially maintained the stability of the smectite model reach their lowest point, the smectite structure will be fully altered, as illustrated in Fig. 11.
In the natural state, before the coal seam was excavated, the rock mass of the roof and floor of the coal seam was protected from water intrusion by water-resistant rock layers. The final state of argillization (Fig. 12) occurs when the fissures that develop in the rock mass are activated under the dynamic forces applied during the excavation;30,31 as the fissures join and converge they form large fissures that act as channels for the permeating water. When the original mudstone is saturated, the water molecules within the crystalline layers move by random Brownian movement and exchange energy with the skeleton molecules of the smectite. Hence, a minimized energy structural system is formed as indicated in Fig. 11. The mechanical properties of the mudstone will be weakened until this property is overall isolated; eventually, the mudstone is transformed into an argillization compound as shown in Fig. 12.32,33
The simulation shows that increasing the number of water molecules will increase the intra-layer space in the structural model of smectite, i.e., the parameter c will be larger. This indicates that the dilation breakage of smectite is always along the direction of c. From a macroscopic prospective, the axial directions of argillization breakage fissures of mudstone are also normal to the direction of c (Fig. 13), which is in good agreement with the MS simulated model.
5 Conclusions
Based on the results of this study, the following conclusions can be drawn:(1) Clay mineral accounts for a large proportion of the sampled mudstone. In the natural state, the microstructure of the samples shows that the clay granules are bonded together into clumps, with other minerals like quartz and feldspar distributed among them. The weak bonding among the clumps induces the formation of pores, which facilitates the penetration of water. Thus, the behaviour of the mudstone is greatly affected by the properties of the clay mineral and its microstructure.
(2) Simulation results from the MS software shows that single, double, and triple layers of water molecules can be added between the double unit cells of smectite when 48, 128 and 224 water molecules are adsorbed between the layers of the cells, respectively. With increased hydration of the mudstone under continuous soaking, the micro structure of the mudstone will be destroyed, coarse granules such as quartz and mica detach, and large fissures develop. These effects induce macroscopic phenomena such as argillization and liquefaction in the mudstone.
(3) With the energy optimization of the smectite model, the polyhedral structures of the smectite molecular model change irregularly and the total energy of the model decreases dramatically. When the intermolecular forces that initially sustained the stability of the smectite model drop to their lowest point, they form an energy-minimized structural system. This causes a notable decrease in the mechanical property of the mudstone, leading to total mechanical failure and argillization of the mudstone material.
(4) The space between the molecular layers grows as the number of water molecules increases during the hydration process of smectite; this demonstrates that the direction of dilation breakage is perpendicular to the direction of the c axis. Moreover, the macroscopic breakage direction of mudstone is parallel to the direction of c, thus confirming the process from the micro prospective.
Acknowledgements
Financial support for this paper was provided by the Natural Science Foundation of Jiangsu Province under contract no. BK20141130, and supported by “the Fundamental Research Funds for the Central Universities” under contract no. 2014QNB27.Notes and references
- X. Xu, Study on water-weakening mechanism and dynamic process control of roadway in argillaceous rock mass, Ph.D, China University of Mining and Technology, Xuzhou, 2007.
- X. Peng, Study on the rheological properties of soft rock and its engineering application, Ph.D, Wuhan University of Technology, Wuhan, 2002.
- Z. Chen and X. Wen, Chin. J. Rock Mech. Eng., 1983, 2, 1–10 Search PubMed.
- Y. Qu, X. Xu, M. Shi and Z. Wu, Hydrogeol. Eng. Geol., 1988, 05, 18–20 Search PubMed.
- J. Xia, J. Nanjing Archit. Civil Eng. Inst., 1994, 28, 31–37 Search PubMed.
- T. Peng, M. He and W. Ma, Hydrogeol. Eng. Geol., 1995, 40–43 Search PubMed.
- C. Zhou, Y. Deng, X. Tan, Z. Liu, W. Shang and S. Zhan, Chin. J. Rock Mech. Eng., 2005, 24, 33–38 Search PubMed.
- J. Ma, G. Cui, Y. Qin and G. Zhou, J. China Univ. Min. Technol., 2008, 18, 122–124 CrossRef.
- L. Tan, Rock Soil Mech., 2001, 22, 1–5 Search PubMed.
- H. Huang and P. Che, J. Tongji Univ., 2007, 35, 866–870 Search PubMed.
- L. Zhang, X. Mao, R. Liu, Y. Li and H. Yin, Int. J. Min. Sci. Technol., 2014, 24, 433–439 CrossRef PubMed.
- K. Yin, D. Zhou, B. Yang, X. Zhang, Q. Xia and R. Xu, Comput. Appl. Chem., 2006, 23, 1335–1340 CAS.
- L. de Pablo, M. Chavez and J. de Pablo, Langmuir, 2005, 21, 10874–10884 CrossRef CAS PubMed.
- T. Liu, X. Tian, Y. Zhao and T. Gao, Chin. Phys. B, 2010, 19, 109101 CrossRef.
- Y. Zheng and A. Zaoui, Solid State Ionics, 2011, 203, 80–85 CrossRef CAS PubMed.
- D. Guerra, I. Mello, L. Freitas, R. Resende and R. Silva, Int. J. Min. Sci. Technol., 2014, 24, 525–535 CrossRef CAS PubMed.
- P. Mignon, P. Ugliengo, M. Sodupe and E. Hernandez, Phys. Chem. Chem. Phys., 2010, 12, 688–697 RSC.
- T. Liu and Y. Chen, Chin. Phys. B, 2013, 22, 406–410 Search PubMed.
- D. Ebrahimi, R. Pellenq and A. Whittle, Langmuir, 2012, 28, 16855–16863 CrossRef CAS PubMed.
- E. Hensen and B. Smit, J. Phys. Chem. B, 2002, 106, 12664–12667 CrossRef CAS.
- V. Aggarwal, Integrating molecular simulations with experiments to study organic pollutant interactions with clay minerals, Ph.D, Michigan State University, 2005.
- M. Nakano, K. Kawamura and Y. Ichikawa, Appl. Clay Sci., 2003, 23, 15–23 CrossRef CAS.
- J. Wang, J. Wang, F. Zeng and X. Wu, Acta Mineral. Sin., 2011, 31, 133–138 CAS.
- J. Xu, Y. Fu, T. Tian, Z. Sun, H. Liu and Z. Sun, Drill. Fluid Completion Fluid, 2012, 29, 1–4 CAS.
- D. Powell, H. Fischer and N. Skipper, J. Phys. Chem. B, 1998, 52, 10899–10905 CrossRef.
- J. Wang, F. Zeng and J. Wang, Acta Chim. Sin., 2006, 16, 1654–1658 Search PubMed.
- P. Na, F. Zhang and Y. Li, Acta Phys.-Chim. Sin., 2006, 22, 1137–1142 CrossRef CAS.
- C. Chang and N. Skipper, Langmuir, 1997, 13, 2074–2082 CrossRef.
- G. Li, Study on the surrounding rock stability and safety control of roadways roof embedded weak intercalated seam, Ph.D, China University of Mining and Technology, Xuzhou, 2008.
- T. Sitharam, J. Sridevi and N. Shimizu, Int. J. Rock Mech. Min. Sci., 2001, 38, 437–448 CrossRef.
- X. Yang, J. Pang, D. Liu, Y. Liu, Y. Tian, J. Ma and S. Li, Int. J. Min. Sci. Technol., 2013, 23, 307–312 CrossRef PubMed.
- W. Feng, R. Huang and Q. Xu, J. Soil Water Conserv., 2009, 16, 26–29 Search PubMed.
- Z. Guo, J. Eng. Geol., 1996, 01, 75–79 Search PubMed.
| This journal is © The Royal Society of Chemistry 2015 |