The effect of the aliphatic carboxylate linkers on the electronic structures, chemical bonding and optical properties of the uranium-based metal–organic frameworks

Abstract

Metal–organic frameworks (MOFs) are drawing increased interest for their high stability and porosity leading to their potential applications in separation, catalysis, and photoelectric processes. Recent studies have identified the role of aminated linkers in band-gap reduction of different MOFs. Uranyl-containing MOFs are of particular interest due to their photo-luminescent properties and their photocatalytic activity. We recently studied the electronic structures of a series of uranyl containing aliphatic dicarboxylate structures that contain aliphatic dicarboxylate linkers of different lengths. Members of this series are UO₂–C₄H₄O₄–H₂O (MOF1), UO₂–C₅H₆O₄ (MOF2), UO₂–C₆H₈O₄–2H₂O (MOF3), UO₂–C₇H₁₀O₄ (MOF4), UO₂–C₈H₁₂O₄ (MOF5), UO₂–C₉H₁₄O₄ (MOF6), and UO₂–C₁₀H₆O₄ (MOF7). This series of actinide coordination polymers were synthesized by various groups. Our computational study provides a detail analysis of chemical bonding, charge distribution, geometric and electronic structural properties, and optical properties of these MOFs for the first time. The variation in the length of linkers does not significantly influence the electronic properties of these MOFs. All MOFs of this series show semiconducting character, common in other transition metal-based MOFs. The band gap for the whole series is essentially constant at ca. 2.5 eV, independent of the length of linkers. For the first time, we provide an extensive analysis of the bonding environment and characteristics in these MOFs based on the charge density distribution, Bader and Mulliken population analysis as well as electron localization functions (ELF). Our analyses show that the uranyl metallic subunit in all MOFs has ionic bonding characteristics. The organic carboxylate linkers, on the other hand, show predominantly covalent bonding characteristics. Simulated optical properties, such as refractive index n(ω), absorption coefficient α(ω), optical conductivity σ(ω), reflectivity R(ω), and electron energy-loss spectrum L(ω) are obtained from the calculated frequency dependent dielectric constants. These properties indicate some promising application of these MOFs as photo-catalyst. In particular, substantial absorption in the energy range of the visible part of electromagnetic spectrum shown by these MOFs can be explored further for application in solar energy sector. Our results also indicate to a possible way to tune the band gap through, e.g., doping, and hence pave the path to a potential application of these MOFs as photocatalysts.

---

I. Introduction

Recent studies are finding new applications of metal–organic frameworks (MOFs) and coordination polymers (CPs). MOFs and CPs are a new class of hybrid porous materials analogous to zeolitic materials. Their applications include but are not limited to photocatalysis,^1,2 catalysis,^6,7 sensing,^8–11 molecular recognition,^12–15 gas adsorption^16–18 and storage,^19–22 and selective separation.^19,23–26 The potential usages of MOFs or CPs are explored in some recent reviews.^27–31

Despite the increasing interest in MOFs and CPs, a fundamental understanding of these materials at the atomic level is limited. A deep understanding of the structure–property relationship, in particular the relationship between structure and its corresponding physicochemical properties is needed to match the material to a particular application. For example, in order to identify the suitability of a MOF as a sensor or photovoltaic material, the relevant information on electronic and optical properties is essential.

In MOFs and CPs, a metal center or poly-nuclear cluster and multifunctional organic linkers are bound together to form the basic unit of the structure. These building units are assembled in extended topologies. Both the coordination environment of the metal center and the structure and steric properties of the organic linkers can influence the functionalities of these materials.

A major part of the research on MOFs is focused on the materials based on transition metals.³² Therefore, the structural predictability and control over topology for these materials can be obtained, to some extent, from the well-understood coordination geometries of transition-metal elements. Consequently, this leads to the design of materials with pre-defined structural motifs and potential applications. However, actinide-based CPs and MOFs are not explored as extensively as their counterparts of transition metal-based MOFs or even lanthanide-based MOFs. Although the coordination chemistry of U(VI) in molecular materials is well developed,³³ synthesis and further studies on the polymeric materials based on the U(VI) topologies have emerged only recently.^3,34,35

The design and synthesis of emerging U-framework materials are driven by the well-established crystal chemistry of U–O polyhedra and the introduction of multifunctional linkers leading to the polymerization of UO₂²⁺ centers through organic backbones. Among the organic linker agents, difunctional carboxylic acids or dicarboxylates are a popular choice as they promote a wide range of structural types and composition through variable sizes and shapes. Therefore, construction of MOFs using dicarboxylate groups provides an effective way of tailoring functionality and controlling structural property (e.g., the pore-size).^31,36–38

Uranium-based metal carboxylate systems are studied in recent years and several structures of synthetic coordination polymers using a series of aliphatic dicarboxylic linkers are reported.^3–5 Members of this series are UO₂–C₄H₄O₄–H₂O (MOF1), UO₂–C₅H₆O₄ (MOF2), UO₂–C₆H₈O₄–2H₂O (MOF3), UO₂–C₇H₁₀O₄ (MOF4), UO₂–C₈H₁₂O₄ (MOF5), UO₂–C₉H₁₄O₄ (MOF6), and UO₂–C₁₀H₁₆O₄ (MOF7). The construction of MOFs in this series utilizes succinate (C₄H₆O₄, in MOF1), glutarate (C₅H₈O₄, in MOF2), adipate (C₆H₁₀O₄, in MOF3), pimelic (C₇H₁₂O₄, in MOF4), suberic (C₈H₁₄O₄, in MOF5), azelaic (C₉H₁₆O₄, in MOF6), and sebaic (C₁₀H₁₈O₄, in MOF7) acids. This series provides a unique opportunity to study the effect of varying length of the organic linkers on the varying functionality of MOFs.

However, besides the synthesis process and structural characterization, very limited information is available about other properties of these MOFs. Important properties such as structural stability, chemical bonding, electronic and optical properties are hardly studied yet for these MOFs. One of the obstacles for experimental studies on uranium MOFs may be the radioactivity of the material. Therefore, computational methods are an alternative tool and used as a virtual laboratory to study the physicochemical and electronic properties of these compounds.

In this report, we present a comprehensive computational study of a series of uranium-based MOFs containing aliphatic dicarboxylate linkers with varying lengths. By applying DFT methods, with the GGA-PBE exchange–correlation functional along with the PAW potentials, as implemented in the VASP package,^39,40 we elucidate the crystal structure, stability, electronic structure, and chemical bonding of these MOFs. Additionally, the optical properties of the series are calculated using the CASTEP^41,42 module of the Material Studio 6.1 package. The analyses of the studied properties provide valuable insight to identify potential applications of these materials, e.g., as photo-catalysts. They also elucidate the systematic trends in the properties as a function of the length of the organic linkers.

II. Computational methods

The calculations have been performed using the projector augmented wave (PAW)^43,44 method within density functional theory (DFT)^45,46 as implemented in the Vienna Ab initio Simulation Package (VASP).^39,40 The exchange–correlation potential is approximated by the generalized gradient approximation (GGA), as parameterized by Perdew, Burke, and Ernzerhof (PBE).⁴⁷ Standard PAW potentials, supplied with the VASP code, are employed in the calculations. The cut-off energy for the plane wave basis was chosen to be 500 eV, and the convergence of self-consistent cycles is assumed when the energy difference between subsequent cycles is less than 5 × 10⁻⁵ eV. The Brillouin zone for different structures and properties is sampled by a Monkhorst–Pack⁴⁸ k-point grid and the k-point sampling density is similar for all considered systems (>800/n k-points where n is the number of atoms in the unit cell). This is a method for generating k-point grids where the k-point grid density kept consistent. This method is implemented in the open-source Python Materials Genomics (Pymatgen) package.⁴⁹ We used a Gaussian smearing of 0.05 eV for the k-point grid. The internal structural parameters were relaxed until the total energy and the Hellmann–Feynman forces on each nucleus were less than 0.02 eV Å⁻¹.

In the case of heavy elements, such as trans-uranium actinides, relativistic effects can be significant. However, due to the considerable computational power required to perform fully relativistic calculations on large systems (160 atoms per unit cell), calculations are performed at the scalar relativistic level. In this approximation, the relativistic effects due to the Darwin and mass–velocity terms are taken into account. VASP treats valence electrons in a scalar relativistic approximation incorporated into the PAW potentials.⁴⁰ The oxidation state of U in these MOFs is VI. Therefore, there are no unpaired electrons that can give rise to a number of issues including electron localization as well as spin orbital coupling (SOC). As a consequence of the lack of unpaired electrons, we neglected spin orbital coupling (SOC) and did not apply DFT+U model in order to account for the effect of electron localizations in this series of calculations.

In order to quantify the distribution of charges and characterize the bonding properties in MOFs of this series, we have performed a Bader analysis⁵⁰ where the atomic volumes are defined solely from the electronic charge density. For this analysis, core charges are included within the projector-augmented wave (PAW) framework. The Bader analysis is performed using the program developed by the Henkelman group.⁵¹ The charge at the atom is obtained by subtracting the Bader charge from the number of valence electrons considered for that particular atom in the density functional theory (DFT) calculations.

The optical properties including dielectric function, absorption coefficient, reflectivity, refractive index, optical conductivity, and energy loss function for the series of MOFs are calculated using the CASTEP code.^41,42 The exchange–correlation functional was approximated with the generalized gradient approximation (GGA) scheme, parameterized by the Perdew–Burke–Ernzerhof (PBE) functional.⁴⁷ An energy cutoff for plane wave expansion of 500 eV was used for all periodic calculations. Ultrasoft pseudopotentials were used to describe core electron behavior, while remaining valence electrons were treated explicitly (e.g., for uranium, 78 electrons are included in the pseudopotential, and the remaining 14 electrons comprise the valence band: [Xe] 5f³ 6s² 6p⁶ 6d¹ 7s²).⁵² Sampling of the Brillouin zone was conducted with a k-point separation of 0.07 Å⁻¹, and self-consistent field cycles were assumed to converge with an energy difference of less than 10⁻⁴ eV.

III. Results and discussions

Structural and geometric parameters

The main features of the structural properties of these MOFs stem from the structural characteristic of its molecular constituents. In particular, the characteristics of uranyl (UO₂²⁺) ions play an important role in defining the topology of these MOFs. U(VI) atoms in the crystal structures usually form a linear triatomic uranyl (UO₂²⁺) cation, whereas O atoms are terminal and form multiple bonds with the U center. Because of these terminal oxygen ligands, any further coordination to the U center occurs on the equatorial plane forming one of the three common square, pentagonal, or hexagonal bipyramids.

The structural characteristics of all seven MOFs studied here follow the common trend of uranyl chemistry. The uranyl building units in these MOFs have either pentagonal or hexagonal bipyramidal coordination spheres. A short structural description of each MOF is given below. The visual representation of the coordination environment of the uranyl inorganic building units and its connectivity to the organic linkers and the polyhedral representation of all MOFs are shown in the ESI in Fig. S1 to S7.†

In MOF1, the uranyl-building units form a pentagonal bipyramids where four equatorial O atoms come from succinate groups and one from a bound water molecule. The individual pentagonal bipyramids are connected by succinate linkers in a bridging bidentate coordination and give rise to the three-dimensional architecture.

The structure of MOF2 consists of two edge-sharing pentagonal bipyramids forming a dimer. Each pentagonal bipyramid consists of a uranyl ion surrounded by five equatorial O atoms from four distinct glutarate anions. Bridging glutarate anions in bidentate coordination connects dimers.

The uranyl building units of MOF3 form a hexagonal bipyramid containing six equatorial O atoms. Four of the six O atoms are from the carboxylate group (adipic acid) and the remaining two from water molecules. The coordination environment of the carboxylate linker with the uranyl unit is in bidentate form.

Pimelic acid molecules in MOF4 connect the uranyl-building units. Uranyl units in MOF4 form dimers of edge-sharing pentagonal bipyramids. Five equatorial O atoms of the bipyramid are from four pimelate molecules. The pimelate carboxylate groups are found in two coordination modes, bridging bidentate and bridging tridentate. Each of the acid molecules is bound in a bridging tridentate coordination at one end of the acid molecule and bridging bidentate coordination at the other.

MOF5 consists of edge-sharing hexagonal bipyramids forming a chain along 100 and connected by suberic acid molecules to other such chains to form a two dimensional topology. The hexagonal bipyramids are constructed of a central uranyl cation with six equatorial O atoms from four distinct subarate molecules. The coordination mode of the carboxylate linker is a bridging tridentate, connecting uranyl at both ends of the acid molecule.

Like MOF5, MOF6 consists of edge-sharing hexagonal bipyramids forming chains propagating in the [010] direction. These chains are then linked by azelaic acid molecules to form two-dimensional sheets. Other structural characteristics of MOF6, such as bridging tridentate connectivity of the linker to metal center, and the formation of hexagonal bipyramids with six equatorial O atoms from four distinct azelate molecules, are also similar to that of MOF5.

The last MOF in this series, MOF7, is composed of uranyl dimers linked by sebacate molecules. The dimer consists of corner-sharing pentagonal bipyramids. These dimers are further connected by sebacate molecules to form two unique layers. These two layers have a distinct coordination of the acid linker molecules to the uranyl dimers. In one layer, two sebacate molecules form a bridging tridentate coordination with the uranyl dimer on one end of the molecule and a bridging bidentate coordination at the opposite end of the molecule. The other layer contains sebacate molecular chains that are bridging bidentate or bridging tridentate at both ends of the linker molecule.

Often, the quality of the collected X-ray intensity data for structural analysis is not very good, particularly for a complex compound such as the MOF or CP. As a result, the structural parameters from the experiment are solved by using a simulated structure. Hence, the ab initio computational methods can be a very useful tool to resolve any ambiguity and uncertainties in the experimentally available structural data for complex solid-state materials. The structural optimization applying ab initio method thus complements the poorly resolved experimental data and help predicting accurate structural properties. Here, we use DFT-based methods to optimize the geometry and structural parameters of MOFs described above.

DFT calculated optimized cell parameters of U-based MOFs in comparison with the measured parameters are presented in Table 1. The geometry optimizations using GGA-PBE functionals with PAW potentials in the VASP computational package is performed without any constrains or symmetry restrictions. The symmetry of the optimized cell is a posteriori determined using the symmetry module in Materials Studio. The analysis of the structural data shows that the computationally optimized structures retain the same crystal system and symmetry as of the measured crystal structures. For MOF1 and MOF4, the crystal symmetry is determined as P2₁/n, keeping the same cell alignment as the measured one from XRD data. This is accompanied with a cell shape change with the β angle changing from 102° to 100° for MOF4. Overall, the computationally optimized structures have more relaxed cell parameters and consequently higher cell volume compared to the measured structural parameter. The cell parameters are about 2–3% larger than the experimental ones, except for MOF3, which has calculated cell parameters that are about 6% larger than their experimental counterparts. Computationally increased cell parameters are a common trend for GGA-PBE functional which systematically overestimate the cell parameter.

Table 1 A comparison of DFT calculated optimized cell geometry parameters of U-based MOFs with the measured parameters

	System	Space group		Lattice parameters (a, b, c) (Å)		Angles (°)		Vol (Å^3)
		Exp.	Calc.	Exp.	Calc.	Exp.	Calc.	Exp.	Calc.
MOF1	Monoclinic	P21/n	P21/n	7.57, 10.78, 9.51	7.54, 11.35, 9.67	90.00, 90.77, 90.00	90.00, 88.52, 90.00	776.0	827.6
MOF2	Monoclinic	P21/c	P21/c	6.05, 9.36, 14.03	6.27, 9.56, 14.24	90.00, 90.50, 90.00	90.00, 92.04, 90.00	793.9	853.5
MOF3	Tetragonal	P43212	P43212	9.63, 9.63, 11.81	10.22, 10.22, 12.33	90.00, 90.00, 90.00	90.00, 90.00, 90.00	1095.6	1288.9
MOF4	Monoclinic	P21/n	P21/n	13.22, 9.44, 16.38	13.60, 9.70, 16.74	90.00, 102.78, 90.00	90.00, 100.26, 90.00	1994.1	2173.7
MOF5	Triclinic	P 1	P 1	4.41, 5.55, 10.72	4.50, 5.75, 10.96	77.47, 81.87, 85.99	75.50, 82.23, 86.48	253.5	271.8
MOF6	Monoclinic	P2/c	P2/c	11.32, 4.40, 10.85	11.67, 4.51, 11.52	98.06, 90.00, 90.00	99.45, 90.00, 90.00	538.3	598.5
MOF7	Triclinic	P 1	P 1	9.50, 14.01, 15.38	9.70, 14.74, 15.45	94.88, 101.27, 94.91	94.30, 101.66, 95.08	1988.5	2145.4

---

Band structure and density of states (DOS)

The effect of structural changes on the electronic structure can be analyzed using the changes in the projected density of state representation. Fig. 1 shows the orbital projected density of state (PDOS) along with the total density of state (TDOS) of MOFs. The principle common feature of the DOS of all MOFs is the orbital compositions of the conduction and valence band. In all MOFs, the conduction band minimum (CBM) has U(5f) contributions, while the valence band maximum (VBM) is dominated by O(2p) orbitals. To some extent, there are minor contributions from U(5f) orbitals to the VBM and from O(2p) to the CBM. However, there are no significant contributions of orbitals from C or H atoms to the CBM or VBM. The other common feature, in particular in MOF1, MOF2, MOF4, MOF6, and MOF7 is the very sharp isolated conduction band minimum with U(5f) character. The structure of the DOS for these MOFs agrees with the DOS structure of U-based coordination polymers calculated in a recent study.⁵³ In the studied U-based coordination polymer, the CBM and VBM mainly have contribution from U(5f) orbitals of uranyl and O(2p) orbitals of organic linkers, respectively. However, such a structure of DOS, where CBM is influenced by the metal center and VBM is affected by the linker agents, is not observed in some alkaline earth metal-based isoreticular MOFs⁵⁴ (e.g., M-IRMOF-10 with M = Cd, Be, Mg, Ca, Sr, Ba). In the case of IRMOF-10C, atoms from the linker are found to be the determining elements of the band gap. In a recent study, observations were made for another series of IRMOF based on a systematic DFT study⁵⁵ that give a different perspective. The results of the investigation on eight IRMOFs with different dicarboxylic acid linkers show that adjustment with the halogen atoms in organic linkers can be used as functional groups to tune the band gap of these IRMOFs.⁵⁵ In contrast, Choi et al. reported⁵⁶ that it is possible to tune electronic band gaps from semiconducting to metallic states by substituting Zn(II) ions in MOF-5 with Co(II) ions.

Fig. 1 The total and orbital projected density of states of MOF1 to MOF7 in subfigures (a) to (g), respectively.

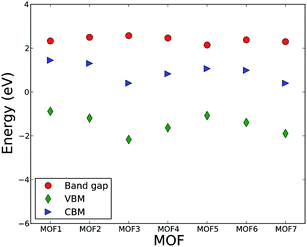
This fact can essentially shed light on the invariability of band gap in response to the change in linker length. The band gaps of all MOFs are presented in Fig. 2 along with the CBM and VBM. Fig. 2 shows that the band gaps of MOFs in this series are essentially the same and the numerical value lies within the range of 2.3 to 2.6 eV. The VBM varies within the range of −0.9 to −2.2 eV, while the CBM is in the range of 0.4 to 1.5 eV. There are some variations in CBM and VBM. However, the variation in the band gap (calculated as the difference between the CBM and VBM) is negligible.

Fig. 2 Band gap, valence band maximum (VBM), and conduction band minimum (CBM) of MOFs.

Unlike IRMOF-10 where C atoms from the linker influence the conduction and valence band DOS, C or H atoms from linkers in this series do not have significant influence on the CBM and VBM. The CBM, as described above, is influenced by the metal center of the metallic node and VBM is influenced by the O atoms of the linkers. This implies that the degree of localization or delocalization of valence electrons of uranyl ions, or the changes in the bonding interaction between uranyl and O, will significantly affect the band gap value of the MOFs in this series. Since C atoms from the linker do not contribute significantly to the valence and conduction band, the change in the length of carboxylate group contributed by the increasing number of CH groups does not influence the band structure of valence and conduction band. Hence, the band gaps and the energy levels of CVM and VBM essentially remain invariant with the change in the number of CH groups of the linker. This result leads us to put forward a hypothesis that various metal ions may be used to control the band gap of MOFs in this series, analogous to the phenomenon observed by Choi et al.⁵⁶ A computational study is currently undergoing to test this hypothesis. It is also interesting to investigate if a second type of linker, in particular with an imine group, has an influence on the optical and electronic properties of MOFs.

In order to analyze the role of linker molecules further and make it clear that the length of the linker in this series of MOFs does not significantly influence electronic properties of the MOFs, particularly the bandgap, we compare the electronic properties of MOF1, MOF2, and MOF4. These three MOFs in this series belong to the same monoclinic crystal system and computationally optimized structures have P2₁/c or P2₁/n symmetry, which are identical but use a different setting. Moreover, the coordination environments of the metal centers to their respective linkers have similar characteristics. Namely, the linkers form a bidentate coordination with the uranyl ion. Thus, the only variable for the evaluation of electronic and optical properties is linker length while keeping symmetry and topology, for the most part, constant. Nevertheless, the band gap and main features of CVM and VBM in the DOS are invariable. This analysis confirms our earlier notion that linkers with variable numbers of CH groups have essentially no influence on the band gap of these MOFs.

Calculations of the band structure using GGA-PBE DFT functional tend to underestimate the band gap in semiconducting materials.^57,58 In particular, this is important for the determination of band gaps of semiconducting oxide materials. One trivial method to address this is to apply a scissor operator to empirically reduce the difference between the measured and calculated band gap. Another popular option is to apply the DFT + U⁵⁹ method where the problem with electron localization in transition and heavy metals is addressed with an energy penalty in form of Hubbard U. Other methods include the hybrid functional (e.g., HSE^60,61 and B3LYP^62,63) and the quasi-particle method within the GW approximation.^64–66 These corrections would be relatively small of the uranium MOFs studied here because U is in the formal oxidation state 6+ and localization of these (formally) non-existent f orbitals is therefore not a major issue. In addition, these hybrid and GW methods are prohibitively computationally expensive for large systems with a series of structures with large unit cell such as the systems studied here. A recent study⁶⁷ has employed the HSE functional to compute the band gaps of MFU-4-type metal–organic frameworks with a large unit cell and found good agreement with the experimental value. However, since the main goal of this study is to investigate the role of linkers on electronic and optical properties of MOFs, i.e., compare the properties of each MOF with the others, application of a scissor operator with same numerical value will not have any effect on such comparison. Furthermore, we assume that the application of an expensive hybrid functional may have minimal effect on the conclusion of this study. Because, regardless of the applied method, the dependence of the band gap on the length of the linker should be clear form the comparison of band gaps in MOFs studied here. Moreover, there is no experimental measurement of the band gap of these MOFs so far. Hence, there is no reference to define the value of such a scissor operator. As already explained in the method section, the oxidation state of U in UO₂²⁺ is 6+ and consequently, there is no unpaired electron in U. Thus, we argue that the application of DFT+U method might not have a significant effect on the band gap calculation in this particular case. Interestingly, a GGA-PBE based DFT calculation found recently the band gap of MOF-5 (IRMOF-1) in a very good agreement with that obtained from.⁵⁴ This result is attributed to the isolated nature of the metal oxide nodes that are expected to act like quantum dots and to the perturbation from the organic linker. In light of this valid argument, the calculated band gap in the MOFs studied here might show a close approximation to the expected real band gap.

Chemical bonding in MOFs

Charge density and electron localization function (ELF). Charge-density analysis and ELF⁶⁸ are powerful tools for characterizing the chemical bonding in complex structures such as MOFs. The charge density and ELF projected on a particular lattice plane for optimal visualization are plotted for MOF1 to MOF7 in Fig. 3 to 9, respectively. First, we analyze the chemical bonding characteristics from the charge density distributions. Charge densities in Fig. 3 to 9 are plotted on lattice plane with Miller indices (−2, 1, 1), (−1, −4, −7), (1, −1, 0), (−1, −16, 16), (0, −1, −2), (0, 0, 1), and (−1, 38, 0) for MOF1 to MOF7, respectively. These charge–density plots clearly show that both the uranyl UO₂ unit and the organic linker group represent a molecule-like subunit. The linker molecule shows the characteristics of normal C–C, C–O, and C–H covalent bonds. The charge distributions around the metal center as well as uranyl O atoms are almost spherical. The nearly spherical charge distribution characterizes the ionic interactions between the metal and oxygen sites. Furthermore, the charge density plots also show that there is a ridge-like region with no noticeable charge density distribution between metal and oxygen sites. This fact further confirms the ionic bonding nature of uranyl subunits of MOFs.

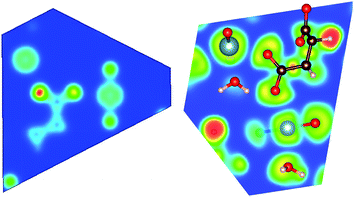Fig. 3 Calculated (a) charge density, and (b) electron localization function (ELF) plots of MOF1 on the (−2, 1, 1) plane.

Fig. 4 Calculated (a) charge density on the (−1, −4, −7) plane, (b) electron localization function (ELF) plots on the (13, 3, 1) plane, and (c) ELF on the (1.4, −1, 3.7) plane of MOF2.

Fig. 5 Calculated (a) charge density, and (b) electron localization function (ELF) plots of MOF3 on the (1, −1, 0) plane.

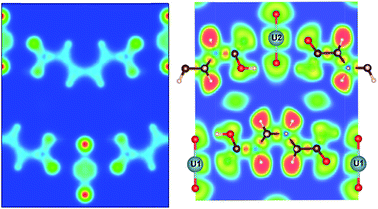
Fig. 6 Calculated (a) charge density, and (b) electron localization function (ELF) plots of MOF4 on the (−1, −16, 16) plane and (c) ELF on (−2.9, 1, 1.85) plane to show the UO₂ bonding environment.

Fig. 7 Calculated (a) charge density, and (b) electron localization function (ELF) plots of MOF5 on the (0, −1, −2) plane.

Fig. 8 Calculated (a) charge density, and (b) electron localization function (ELF) plots of MOF6 on the (0, 0, 1) plane.

Fig. 9 Calculated (a) charge density, and (b) electron localization function (ELF) plots of MOF7 on the (−1, 38, 0) plane.

In order to analyze the chemical bonding environment in these MOFs in a quantitative way, we calculated the ELF. By definition, the ELF quantifies the probability of finding an electron pair in the region of molecule space.^68,69 The range of possible numerical values for ELF is 0 ≤ ELF ≤ 1, analogous to values for probability. The upper limit of ELF is 1 and identified by the region where there is no chance of finding two electrons with the same spin. This limit corresponds to perfect localization. The region where such localization occurs is characterized by the paired electrons to form a covalent bond, lone pairs (filled core levels), or an unpaired lone electron of a dangling bond. The region, where the value of ELF is close to 0.5, corresponds to the presence of homogeneous electron gas. Values of this order indicate regions with bonding of a metallic character. In the region, where electrons are highly delocalized or no electron density exists (vacuum), the ELF is close to 0. Note that ELF is not a measure of electron density, but a measure of the Pauli exclusion principle, and is useful in distinguishing metallic, covalent, and ionic bonding. From this point of view, ELF preserves the notion of an electron pair as the central element of the chemical bonding theory.

The ELFs presented in Fig. 3 to 9 are plotted on different lattice planes with different Miller indices for each MOF. The corresponding Miller indices of the lattice plane are indicated in the figure caption. Since the metal oxide bond and the linker molecule do not lie on the same plane, ELFs for MOF2 and MOF4 are presented on two lattice planes to show the electron localization of the linker as well as the metal subunits. The color code corresponding to the red regions mean high localization and the blue regions indicate low localization. There are some common bonding characteristics in all MOFs in this series that can be inferred from the ELFs presented in Fig. 3 to 9. All ELF plots showing the large value of ELF between neighboring C atoms indicate the strong covalent nature of the C–C bond. Similarly, the relatively high value (≥0.5) of ELF between the C and O atoms also indicates the covalent bonding nature of C–O bonds. An indication of local polarizability, visible as the non-spherical charge localization around H atoms in linker molecules, is found in the ELF distribution at the H sites in the MOF of this series indicating polar covalent bonding. The ELF value between U and O sites is negligibly small. The ELF value at the U sites is distributed spherically. Therefore, it can be inferred that the predominant bonding between U and O is ionic in nature. The ELF findings further confirm the predominant covalent bonding in the linker and ionic bonding between U and O atoms of metallic sub units.

Charge analysis. Atomic charges in molecules or crystalline solids are not clearly defined in quantum chemical theory. The most relevant parameter, that can be determined with the quantum chemical theory, is the electronic charge density. However, there is no unique way to partition the continuous electronic charge density to identify how many electrons are associated with fragments of the system such as atoms or molecules or a group of atoms in a solid. In quantum chemistry, due to its simplicity, the most commonly used partitioning scheme is the Mulliken analysis.⁷⁰ However, this approach is predicated on localized basis sets and, hence, results obtained from this method are sensitive to the choice of atomic basis. As a result, Mulliken population analysis is considered more of a qualitative than a quantitative approach.

In the framework of a plane-wave basis set scheme, the partitioning of the electron density into atomic charges is quite difficult. We use the Bader charge analysis method based on a topological approach (Atoms in Molecules, AIM⁵⁰). In the Bader charge (BC) analysis, an atomic volume is defined as the region of space (called a Bader region) including the nucleus surrounded by a surface that runs through minima of the charge density, and the total charge of an atom is determined by integration of electron density within the Bader region. The minima of the charge density are defined at the positions where the density gradient reaches zero.

The population analysis to identify the number of electrons associated with a particular atom and the populations between atoms is a useful tool for the understanding bonding interactions related to charge transfer between the atoms. The population analysis of the MOFs applying the Mulliken and Bader scheme are shown in Table 2. Along with the calculated Mulliken effective charges (MEC) and Bader charge (BC), the Hirshfeld charges (HC) are also presented in Table 2 for comparison. The Bader charges are calculated from the charge density obtained from the VASP calculations. The Mulliken and Hirshfeld charges are obtained from CASTEP results. Atomic charges of MOFs calculated with the three different schemes confirm the common trend among these schemes observed in previous studies, i.e., BC > MEC > HC.

Table 2 Calculated Mulliken effective charges (MEC), Hirshfeld charges, and Bader charges (BC) for the MOFs in the U-MOF series (carboxyl-C is denoted with an*)

Element	MEC	HC	BC
MOF1
U	1.9	0.77	3.03
O_U	−0.38	−0.27	−0.89
C1*	0.56	0.22	2.66
C2	−0.53	−0.07	0.01
C3	−0.52	−0.07	0.04
C4*	0.57	0.22	2.65
O1	−0.84	−0.21	−1.73
O2	−0.53	−0.19	−1.74
O3	−0.58	−0.19	−1.74
O4	−0.58	−0.18	−1.74
H	0.34	0.09	0.08
MOF2
U	1.87	0.77	3.01
O_U	−0.38	−0.27	−0.9
C1*	0.54	0.21	2.6
C2	−0.52	−0.06	0.05
C3	−0.46	−0.06	0.03
C4	−0.53	−0.07	0.03
C5*	0.57	0.23	2.65
O1	−0.58	−0.19	−1.69
O2	−0.52	−0.18	−1.75
O3	−0.53	−0.19	−1.7
O4	−0.53	−0.19	−1.73
H	0.25	0.05	0.05
MOF3
U	1.86	0.73	2.99
O_U	−0.41	−0.3	−0.93
C1*	0.61	0.23	2.62
C2	−0.56	−0.07	0.07
C3	−0.49	−0.06	0.07
C4	−0.49	−0.06	0.04
C5	−0.56	−0.07	0.02
C6*	0.61	0.23	2.62
O1	−0.81	−0.33	−1.56
O2	−0.57	−0.1	−1.56
O3	−0.81	−0.33	−1.81
O4	−0.57	−0.1	−1.81
H	0.33	0.08	0.03
MOF4
U	1.9	0.77	3.01
O_U	−0.38	−0.28	−0.9
C1*	0.54	0.21	2.6
C2	−0.53	−0.06	0.02
C3	−0.47	−0.07	0.07
C4	−0.47	−0.06	0
C5	−0.47	−0.06	0.07
C6	−0.53	−0.07	0.04
C7*	0.58	0.23	2.65
O1	−0.58	−0.19	−1.69
O2	−0.52	−0.18	−1.75
O3	−0.53	−0.19	−1.72
O4	−0.53	−0.19	−1.71
H	0.24	0.04	0.02
MOF5
U	1.9	0.76	3.01
O_U	−0.37	−0.27	−0.89
C1*	0.53	0.21	2.61
C2	−0.52	−0.07	0.02
C3	−0.46	−0.07	0.02
C4	−0.46	−0.06	0.06
C5	−0.46	−0.06	0.05
C6	−0.52	−0.07	0.06
C7	−0.46	−0.07	0.09
C8*	0.53	0.21	2.61
O1	−0.56	−0.18	−1.7
O2	−0.53	−0.18	−1.7
O3	−0.56	−0.18	−1.72
O4	−0.53	−0.18	−1.72
H	0.24	0.04	0.01
MOF6
U	1.83	0.77	3.07
O_U	−0.38	−0.29	−0.92
C1*	0.55	0.21	2.66
C2	−0.55	−0.07	0.05
C3	−0.49	−0.07	0.05
C4	−0.49	−0.06	0.06
C5	−0.49	−0.06	0.06
C6	−0.55	−0.07	0.06
C7	−0.49	−0.07	0.08
C8	−0.49	−0.06	0.08
C9*	0.55	0.21	2.66
O1	−0.55	−0.18	−1.73
O2	−0.57	−0.18	−1.73
O3	−0.55	−0.18	−1.72
O4	−0.57	−0.18	−1.72
H	0.26	0.04	−0.01
MOF7
U	1.89	0.78	3.02
O_U	−0.39	−0.27	−0.89
C1*	0.58	0.23	2.65
C2	−0.53	−0.07	0.05
C3	−0.47	−0.06	0.08
C4	−0.47	−0.06	0.08
C5	−0.47	−0.06	0.04
C6	−0.47	−0.07	0.05
C7	−0.54	−0.07	0.05
C8	−0.47	−0.06	0.08
C9	−0.53	−0.07	0.07
C10*	0.55	0.22	2.67
O1	−0.53	−0.19	−1.73
O2	−0.52	−0.18	−1.72
O3	−0.53	−0.19	−1.69
O4	−0.53	−0.19	−1.76
H	0.24	0.04	0

---

The calculated Mulliken effective charges (MEC, Table 2) of U atoms and O atoms in the uranyl metal oxide unit (denoted O_U in the Table 2) are invariable in all MOFs in the series and close to +1.9 and −0.4 |e|, respectively. Such a population distribution indicates the partial electron transfer from U to O and the ionic character of UO₂. The carboxylate C atoms that connect to the O atoms bear positive charges and all other C atoms have negative charges. The positive charges of marginal C atoms in all MOFs are fairly consistent and vary slightly between +0.53 to +0.61. All O atoms of the linker carry negative charges and vary in the range of −0.52 to −0.81 |e|.

The results of the topological population analysis with the Bader scheme are presented in Table 2. The population analysis with Bader scheme shows similar characteristics to Mulliken analysis. The Bader atomic charges of U and O in uranyl metallic center are about +3.0 and −0.9 |e|, respectively. These results indicate that the interaction between U and O is ionic and three electrons are transferred from U to O. The resulting charges are +1.2 |e| on the uranyl ion and −1.2 |e| on the linker ion. This is a consistent feature of population distribution in all MOFs in this series. The invariant charge distribution in metallic center indicates negligible effects of the length of carboxylate linkers on the charge distributions in the metallic units. Overall, the population analysis shows a consistent result with the charge density and ELF analyses.

Optical properties. Optical phenomena such as reflection, absorption, and refraction can be quantified by a number of parameters and these parameters determine the optical properties of the material at the macroscopic level. The fundamental parameter that primarily relates the linear electronic response of the system to electromagnetic radiation is the complex dielectric constant. The frequency-dependent dielectric function, ε(ω), considered here relates the interaction of photons with electrons. It is common practice to evaluate the complex dielectric constant in the calculation first and then express other properties in terms of it. In CASTEP, the imaginary part of the complex dielectric constant, ε₂(ω), is calculated as a function of the angular frequency and the vector defining the polarization of the incident electric field. Such an expression of the imaginary part of the dielectric function is similar to Fermi's Golden rule for time-dependent perturbations, and can be derived from interband optical transitions between the occupied and unoccupied bands including appropriate momentum matrix elements to take care of the selection rules. The real part of the dielectric constant ε₁(ω) is then obtained through a Kramers–Kronig transform that relates the imaginary and real part of the dielectric constant.⁷¹ The real part of ε₁(ω) in the limit of zero energy (or infinite wavelength) is equal to the square of the refractive index n(ω). All frequency-dependent linear optical properties, such as refractive index n(ω), absorption coefficient α(ω), optical conductivity σ(ω), reflectivity R(ω), and electron energy-loss spectrum L(ω), can be derived from the imaginary and the real part of dielectric functions ε(ω). The inter-relationship between frequency-dependent linear optical properties shows that, in general, the real part of the dielectric constant determines the refractive index, while the imaginary part determines the absorption coefficient. The extinction coefficient is directly proportional to the absorption coefficient.

Some approximations and simplifications are used in optical property calculations to make the calculation computationally tractable. For example, the local field effect is not taken into account with the level of approximation used in CASTEP. The local field effect arises from the phenomenon in which the electric field experienced at a particular site in the system is screened by the polarizability of the system itself. As a result, the local field can be different from the applied external field (that is, the photon electric field). This effect can significantly change the frequency-dependent optical properties. However, including this effect into calculation is prohibitively expensive for general systems. Along with the absence of local field effects, excitonic effects are not treated in CASTEP calculations. The nonlocal nature of the GGA functionals is not taken into account when evaluating the matrix elements but it is expected that this will have a small effect on the calculated spectra. Phonons and their optical effects are also neglected.

The calculated optical properties, applying the CASTEP software package, of the series of MOFs studied here are presented in Fig. 10 to 15 for dielectric functions ε(ω), absorption coefficient α(ω), refractive index n(ω), optical conductivity σ(ω), reflectivity R(ω), and electron energy-loss spectrum L(ω). All MOFs in this series show similar optical properties except for MOF5. We discuss the common characteristics of optical properties of the members of this series and separately discuss the distinct optical properties of MOF5.

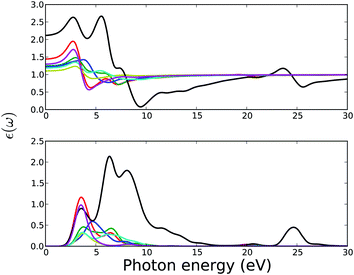Fig. 10 Calculated real (upper plot) and imaginary (lower plot) part of the complex dielectric function of MOFs. Legends for the lines are the same as in Fig. 11.

Spectra of the real and imaginary parts of the complex dielectric constant as function of the photon energy of MOFs are presented in Fig. 10. The interpretation of these spectra in terms of electronic structure, presented in the Fig. 1, reveals the manner by which the compound absorbs the incident radiation. The low-energy parts of the spectra (from ca. 2.5 to 10.0 eV) are characterized by a sharp peak and a shallow or shoulder peak for all MOFs except MOF5. These peaks can be assigned to a particular electronic transition from the top of the valence band to the isolated low-energy block in the conduction band as presented in the DOS spectra in Fig. 1.

In MOF1, the low-energy peak of the imaginary part of the complex dielectric function ε₂(ω) at around 3.5 eV arises mainly from O(2p) → U(5f) and the next shallow peak at around 7.2 eV from the U(5f) → O(2p) interband transitions. Analogous interband transitions give rise to the first and second peak of ε₂(ω) in the low energy range of 2.5 to 10 eV for MOF2, MOF3, MOF4, and MOF6. In MOF7, the second peak mainly arises from the C(2p) → O(2p) transition.

Structurally, MOF5 has the smallest unit cell consisting of only one uranyl ion and an organic linker of suberic (C₈H₁₄O₄) acid. Electronically, the conduction band is different from the conduction band of all other MOFs in this series. Instead of a sharp narrow band, characteristic of all other MOFs, the conduction band of MOF5 is broadened with a shoulder peak. These factors are reflected in the optical spectra of MOF5. There are three distinct peaks of the imaginary part of the complex dielectric function ε₂(ω) at the low energy range. These peaks mainly arise from the O(2p) → U(5f) transition at 3.2 and 6.2 eV and U(5f) → O(2p) interband transitions at 7.8 eV.

The real part of the dielectric function ε₁(ω) can be used to estimate the refractive index n(ω) at infinite wavelength or at zero energy (i.e., at n(0)). The estimated refractive index at zero energy n(0) for MOF1, MOF2, MOF3, MOF4, MOF6, and MOF7 are in the range of 1.2 to 1.5. The estimated refractive index of MOF5 is 2.2. At low frequency, i.e., below 2.5 eV, ε₂(ω) is zero for all MOFs, which consistently reflects the band gap of MOFs in this series. Since all other optical properties are deduced from the dielectric functions, the spectral characteristics of the dielectric functions are reflected in other optical properties.

The frequency-dependent optical reflectivity of MOFs is presented in Fig. 11. The reflectivity depends on both real and imaginary part of the dielectric constant. Hence, the spectral characteristics of the dielectric constant are present in the reflectivity. The number of peaks and their sources as the transition bands in the reflectivity spectra for all MOFs are the same as in the dielectric constant and described above. Beyond 30 eV of photon energy, the reflectivity approaches zero for all MOFs. This means that these MOFs do not reflect electromagnetic waves at high frequencies (high UV). Interestingly, MOF5 shows a reflectivity peak at ca. 25 eV indicating its ability to reflect electromagnetic waves at this range. At infinite wavelength (zero energy), the values of reflectivity are 0.008, 0.003, 0.002, 0.0006, 0.03, 0.002, and 0.004 for MOF1 to MOF7, respectively. These numbers indicate that there is no particular trend in reflectivity of these MOFs that primarily differs by the length of their organic linkers. Overall, the reflectivity of this series of MOFs is not high. In the visible part of the electromagnetic spectrum, the reflectivity does not exceed 6%. However, MOF5 has about 16% reflectivity in the UV range. The low reflectivity of these MOFs is consistent with some other MOFs such as M-IROF-1 and M-IROF-10. This is a desirable property for materials used in optoelectronic technologies (e.g., solar cells, LEDs) and can increase the potential of these MOFs.

Fig. 11 Calculated reflectivity of U-based MOFs.

Fig. 12 shows the optical conductivity of MOFs as a function of photon energy. Again, the peak number and position correspond to the peaks described for dielectric constants. As semiconductors, these MOFs do not show any photoconductivity below the band gap energy. Overall, the photoconductivity is low for this series of MOFs.

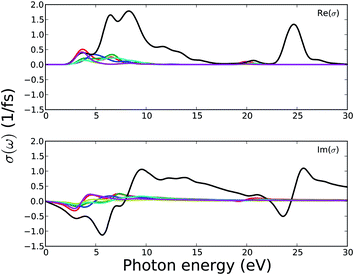Fig. 12 Calculated optical conductivity of MOFs. Legends for the lines are same as in Fig. 11.

The electron energy-loss spectrum, L(ω), primarily describes the energy loss of a fast electron traversing in the material. The peaks in the L(ω) spectrum are associated with the characteristics of the plasma resonance and are related to the plasma oscillation.⁷² The most prominent peak in the energy-loss spectrum can be identified as a plasmon peak. The peak position indicates the frequency of collective excitation of the electronic charge density in the crystal and the corresponding frequency is the so-called plasma frequency. The positions of the plasmon peaks correspond to the transformation from negative ε₁(ω) to positive ε₁(ω). The associated plasma frequency represents a limit above which the material is a dielectric and below which the material has metallic aspects. In addition, the peaks of the L(ω) spectra overlap the trailing edges in the reflection spectra. Fig. 14 shows that the plasmon peaks are at 5.7, 6.1, 6.6, 7.0, 10.7, 5.1 and 5.1 eV for MOF1 to MOF7 respectively. The other peaks in the simulated electron energy loss spectra are associated with the interband transitions. Since no multiple crossings of zero by ε₁(ω) are observed in the frequency dependent dielectric function (Fig. 10), any additional plasmon type excitations are not expected.

Fig. 13 Calculated refractive index (upper) and extinction coefficient (bottom) of MOFs. Legends for the lines are same as in Fig. 11.

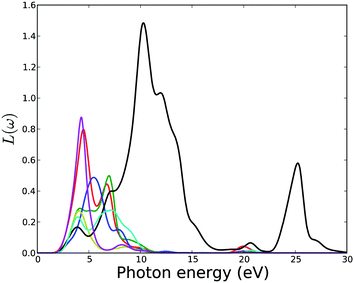Fig. 14 Calculated electron energy loss function of MOFs. Legends for the lines are same as in Fig. 11.

The calculated normal refractive indices (real part of the complex refractive index) and the extinction coefficients κ(ω) (imaginary part of the complex refractive index) are presented in Fig. 13. Non-zero extinction coefficients κ(ω) lead to an exponential decay of the incident electromagnetic wave in the material and the real part of the refractive index determine the phase velocity of the wave front. All MOFs except MOF5 show non-zero extinction coefficients in the photon energy range of 2.5 to 10 eV and reflect the characteristic of the imaginary part of the dielectric functions. MOF5 has non-zero extinction coefficients in the photon energy range of 2.5 to 17 eV and 23 to 27 eV.

Fig. 15 shows the absorption coefficient of the MOFs. The absorption band of MOFs except MOF5 ranges from ca. 2.0 eV to 12.0 eV. All six MOFs have two absorption peaks in this range.

Fig. 15 Calculated absorption spectra of U-based MOFs. Green shaded area represents the energy range of the narrow visible part of the electromagnetic spectrum. Absorption spectra in the visible range are zoomed-in and plotted as the inset. Legends for the lines are same as in Fig. 11.

The first peak for MOF1, MOF2, MOF4, MOF6, and MOF7 is at around 4.1 eV and of these first peaks, the ones of MOF1 and MOF7 are sharp. The first peak of MOF3 at around 5.0 eV is broader. The first peaks of MOF2 and MOF7 are shoulder peaks. MOF5 has a very broad range of absorption band spreading from 2 to 30 eV. The inset of Fig. 15 shows the absorption spectra in the visible range of the electromagnetic spectrum. The different optical properties of MOF5 compared to the optical properties of other MOFs in this series can potentially be attributed to the unique electronic structure of this MOF. As explained above, and seen in PDOS of MOF5 in Fig. 1, the conduction band of MOF5 has different features than the conduction band of other MOFs in this series. The conduction band of MOF5 is broadened. We speculate that such a broadened band can facilitate interband transitions, which is in turn reflected in the enhanced optical properties such as a broad absorption band. Interestingly, all members of this series of MOFs show substantial absorption of visible light and, therefore, may be considered for further studies for the application in solar energy harvesting or photo-catalytic waste remediation.

IV. Conclusions

In summary, we have carried out a detailed investigation of the structural, electronic, and optical properties of U-based MOFs with a series of carboxylate linkers. By analysis of the atomic and electronic structure, including the band structures and the optical properties, we obtained the following important conclusions on this series of MOFs.

The geometry optimization applying DFT based computational methods show that the symmetry groups, defined from the XRD data, are preserved during the full optimization and the relaxation of the respective unit cells are minimal compared to the experimentally measured volume. Lattice parameters and lattice angles are also close match for the experimentally measured parameters. The clearly identified positions of all atoms, particularly light atoms like hydrogen from computational geometry optimizations demonstrate that it is a useful complementary method to experiments in order to accurately determine the equilibrium structural parameters for complicated MOFs.

The chemical environment and bonding nature in these MOFs are analyzed using electronic charge density distribution, electron localization function, Mulliken effective charge, and Bader topological analysis. These analyses show, consistently, that the bonding nature of the uranyl subunit is ionic and the bonding characteristics of C–O, C–H and C–C bonds in organic linker subunits are predominantly covalent. The density of states and electronic band structures are analyzed in order to identify the effect of different linkers on the electronic structures of MOFs in this series. Our analyses show that the most prominent features of the electronic structure, the VBM and CBM, are dominated by the electronic contribution from O(2p) and U(5f) orbitals. Since the length of the carboxylate linkers are controlled by the number of C–C bond, changes in the linker with addition of C–C groups have insignificant influences on VBM or CBM. Further analyses of the band structure, applying GGA-PBE functional, show that the band gaps of these MOFs are invariable with the change in carboxylate linkers. The absolute value of the band gap of these MOFs might change with the application of an expensive hybrid functional such as HSE, but since there is not much dependence of the band gap on the linker, no significant difference with the linker would be expected from the application of an HSE functional. In addition, the MOFs in this series are calculated to be semiconductors with essentially a constant band gap at ca. 2.5 eV. It also indicates that a partial doping with different metals may allow the tuning of band gap values in this series.

With our calculated optical properties, we hope to motivate further experimental studies. The optical properties of MOFs analyzed here, provide useful information about the potential of these materials for application in opto-electronics and photo-catalysis. In particular, all of the MOFs in this series show very high absorbance and low reflectivity, especially at the visible range of solar spectrum.

Even though compromises had to be made on the computational rigor due to the sizes of the unit cells, this study provides, so far, the only computational findings on the electronic structure, band characteristics, and optical properties on these U-based MOFs. There are also no experimental results on the optical and electronic properties available for these MOFs. Our results, hence, are an important contribution to identify potential applications of these materials. They indicate that fine-tuning of the material in terms of the width of the bandgap cannot be done by changing the length of the linker but rather the composition of the metal cation center or the electronic properties of the organic linker. Furthermore, the importance of our results lie in the fact that the computational studies performed here help avoiding the handling of radioactive materials associated with these U-based MOFs in experimental setups and serve as a primary screening tool for determining properties. The studied electronic and optical properties of these MOFs are promising for potential use in hybrid solar cells, organic semiconductors, and photo-catalysts for environmental remediation.

Acknowledgements

This study is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences/Heavy Element Chemistry under Award Number DE-FG02-06ER15783. Computational resources were supplied in part by the NSF XSEDE Science Gateways program.

References

1. C. H. Hendon, D. Tiana, M. Fontecave, C. Sanchez, L. D'Arras, C. Sassoye, L. Rozes, C. Mellot-Draznieks and A. Walsh, J. Am. Chem. Soc., 2013, 135, 10942–10945.
2. W. Chen, H.-M. Yuan, J.-Y. Wang, Z.-Y. Liu, J.-J. Xu, M. Yang and J.-S. Chen, J. Am. Chem. Soc., 2003, 125, 9266–9267.
3. J. Y. Kim, A. J. Norquist and D. O'Hare, Dalton Trans., 2003, 2813–2814.
4. L. A. Borkowski and C. L. Cahill, Inorg. Chem., 2003, 42, 7041–7045.
5. L. A. Borkowski and C. L. Cahill, Cryst. Growth Des., 2006, 6, 2241–2247.
6. A. Corma, H. Garcia and F. X. Llabres i Xamena, Chem. Rev., 2010, 110, 4606–4655.
7. B. Liu, S. Jie and B. Li, Prog. Chem., 2013, 25, 36–45.
8. L. Ai, L. Li, C. Zhang, J. Fu and J. Jiang, Chem.–Eur. J., 2013, 19, 15105–15108.
9. L. He, Y. Liu, J. Liu, Y. Xiong, J. Zheng, Y. Liu and Z. Tang, Angew. Chem., Int. Ed., 2013, 52, 3741–3745.
10. L. Sun, H. Xing, J. Xu, Z. Liang, J. Yu and R. Xu, Dalton Trans., 2013, 42, 5508–5513.
11. X. Wu, M. S. Bharara, B. K. Tate, S. A. Tonks, J. Z. Vilseck and A. E. V. Gorden, in Actinides 2008-Basic Science, Applications and Technology, ed. D. K. Shuh, B. W. Chung, T. AlbrechtSchmitt, T. Gouder and J. D. Thompson, 2008, vol. 1104, pp. 143–149.
12. B. Chen, S. Xiang and G. Qian, Acc. Chem. Res., 2010, 43, 1115–1124.
13. J. Cui, N. Gao, C. Wang, W. Zhu, J. Li, H. Wang, P. Seidel, B. J. Ravoo and G. Li, Nanoscale, 2014, 6, 11995–12001.
14. P. Kumar, P. Kumar, L. M. Bharadwaj, A. K. Paul and A. Deep, Inorg. Chem. Commun., 2014, 43, 114–117.
15. W. Lu, Z. Wei, Z.-Y. Gu, T.-F. Liu, J. Park, J. Park, J. Tian, M. Zhang, Q. Zhang, T. Gentle III, M. Bosch and H.-C. Zhou, Chem. Soc. Rev., 2014, 43, 5561–5593.
16. H. R. Abid, G. H. Pham, H.-M. Ang, M. O. Tade and S. Wang, J. Colloid Interface Sci., 2012, 366, 120–124.
17. S. Barman, H. Furukawa, O. Blacque, K. Venkatesan, O. M. Yaghi and H. Berke, Chem. Commun., 2010, 46, 7981–7983.
18. S.-N. Kim, J. Kim, H.-Y. Kim, H.-Y. Cho and W.-S. Ahn, Catal. Today, 2013, 204, 85–93.
19. Functional Metal–Organic Frameworks: Gas Storage, Separation and Catalysis, ed. M. Schroder, 2010, vol. 293, pp. 1–262.
20. R. Babarao and J. Jiang, Langmuir, 2008, 24, 6270–6278.
21. H. Furukawa and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 8875–8883.
22. Y. H. Hu and L. Zhang, Adv. Mater., 2010, 22, E117–E130.
23. E. D. Bloch, W. L. Queen, R. Krishna, J. M. Zadrozny, C. M. Brown and J. R. Long, Science, 2012, 335, 1606–1610.
24. D. Britt, H. Furukawa, B. Wang, T. G. Glover and O. M. Yaghi, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20637–20640.
25. J. R. Li, J. Sculley and H. C. Zhou, Chem. Rev., 2012, 112, 869–932.
26. P. Nugent, Y. Belmabkhout, S. D. Burd, A. J. Cairns, R. Luebke, K. Forrest, T. Pham, S. Ma, B. Space, L. Wojtas, M. Eddaoudi and M. J. Zaworotko, Nature, 2013, 495, 80–84.
27. H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. O. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428.
28. N. Linares, A. M. Silvestre-Albero, E. Serrano, J. Silvestre-Albero and J. Garcia-Martinez, Chem. Soc. Rev., 2014, 43, 7681–7717.
29. M. Eddaoudi, D. F. Sava, J. F. Eubank, K. Adil and V. Guillerm, Chem. Soc. Rev., 2015, 44, 228–249.
30. J.-C. G. Buenzli, J. Coord. Chem., 2014, 67, 3706–3733.
31. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 974.
32. C. L. Cahill, D. T. de Lill and M. Frisch, CrystEngComm, 2007, 9, 15–26.
33. F. Weigel, in The chemistry of the actinide elements, ed. J. J. Katz, L. R. Morss and G. T. Seaborg, Chapman and Hall., United Kingdom, 1986.
34. J. Y. Kim, A. J. Norquist and D. O'Hare, Chem. Mater., 2003, 15, 1970–1975.
35. M. Frisch and C. L. Cahill, Dalton Trans., 2006, 4679–4690.
36. X. Kong, H. Deng, F. Yan, J. Kim, J. A. Swisher, B. Smit, O. M. Yaghi and J. A. Reimer, Science, 2013, 341, 882–885.
37. O. M. Yaghi, M. O'Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Nature, 2003, 423, 705–714.
38. H. Li, M. Eddaoudi, M. O'Keeffe and O. M. Yaghi, Nature, 1999, 402, 276–279.
39. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
40. J. Hafner, J. Comput. Chem., 2008, 29, 2044–2078.
41. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
42. M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744.
43. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
44. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
45. P. Hohenberg and W. Kohn, Phys. Rev. B: Condens. Matter Mater. Phys., 1964, 136, B864–B871.
46. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, 1133–1138.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
48. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
49. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319.
50. R. F. W. Bader, Atoms in molecules: a quantum theory, Clarendon Press ; Oxford University Press, Oxford [England], 1994.
51. G. Henkelman, A. Arnaldsson and H. Jonsson, Comput. Mater. Sci., 2006, 36, 354–360.
52. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
53. S. Saha and U. Becker, Microporous Mesoporous Mater., 2015 , Submitted.
54. L.-M. Yang, P. Ravindran, P. Vajeeston and M. Tilset, RSC Adv., 2012, 2, 1618–1631.
55. H. Q. Pham, M. Toan, P.-T. Nguyen-Nguyen, Y. Kawazoe, H. Mizuseki and N.-M. Duc, J. Phys. Chem. C, 2014, 118, 4567–4577.
56. J. H. Choi, Y. J. Choi, J. W. Lee, W. H. Shin and J. K. Kang, Phys. Chem. Chem. Phys., 2009, 11, 628–631.
57. S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104.
58. H. Xiao, J. Tahir-Kheli and W. A. Goddard III, J. Phys. Chem. Lett., 2011, 2, 212–217.
59. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767–808.
60. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
61. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906.
62. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
63. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
64. F. Aryasetiawan and O. Gunnarsson, Rep. Prog. Phys., 1998, 61, 237–312.
65. M. Shishkin and G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 235102.
66. M. van Schilfgaarde, T. Kotani and S. Faleev, Phys. Rev. Lett., 2006, 96, 226402.
67. P. Sippel, D. Denysenko, A. Loidl, P. Lunkenheimer, G. Sastre and D. Volkmer, Adv. Funct. Mater., 2014, 24, 3885–3896.
68. A. Savin, A. D. Becke, J. Flad, R. Nesper, H. Preuss and H. G. Vonschnering, Angew. Chem., Int. Ed., 1991, 30, 409–412.
69. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
70. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
71. M. Fox, Optical Properties of Solids, OUP, Oxford, 2010.
72. R. F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope, Plenum Press, 1996.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra01335f

---