Giant actuation in bulk carbon nanotubes under coupled electric and magnetic fields

Abstract

We report an enhanced actuation in bulk carbon nanotubes (CNTs) under coupled electric and magnetic fields, which is much higher than that evaluated in the presence of individual fields. Coupled electric and magnetic fields induce a directional actuation demonstrating a transformation from polarity independent to dependent actuation behavior of CNTs. Both qualitative and quantitative analyses are performed to understand this transformation in the bulk CNTs. Moreover, actuations along radial and axial directions of CNTs have also demonstrated a similar directional behavior.

---

1. Introduction

Carbon nanotube (CNT) based actuators have gained much attention due to their high thermal stability¹ and current carrying capacity at a low operating voltage.² The low operating condition provides a much faster response compared to other conventional actuators.^3,4 A CNT based electrolytic actuator was reported, where strain was induced in the film through the formation of a double-charge layer on the CNT surface.⁵ In another study, C–C bond stretching was observed in a thin film of single walled carbon nanotubes due to the electric field.⁶ Polarity independent and asymmetrical actuation were also demonstrated in a three-dimensional structure of CNTs, where the ends of the bulk CNTs were embedded in a thin conducting film of a polymer.⁷ The polymer embedded bulk CNTs showed ultra-high actuation at a very low electric field compared to other studies on CNT polymer composites.^8,9 Moreover, the actuation response in CNT structures can further be enhanced by coupling two different fields i.e. electric, optical and magnetic fields. Many theoretical and experimental observations have revealed a better performance of the actuators under the coupled field as compared to the individual applied fields.^10–12 For example, the coupling of optical and electrical fields resulted in much higher actuation as compared to the individual field.¹³ Another study has reported the coupled electro-mechanical behavior of the bulk CNT, where the induced strain increases in response to an electric field in an electrolyte environment.¹⁴

On the other hand, coupling of electron spin with the magnetic field in nano-mechanical resonators has also been reported.¹⁵ Magnetic field causes a change in the electronic property of the CNT, which in turn, changes its inherent characteristics.¹⁶ Hence, the actuation of the bulk CNT under electro-magnetic field is a novel phenomenon, which is the motivation of present study. We have evaluated actuation behavior of the bulk CNT under coupled electric and magnetic fields. An enhanced actuation was observed as compared to the response with only electric field, which has been supported by a mathematical model.

2. Experimental section

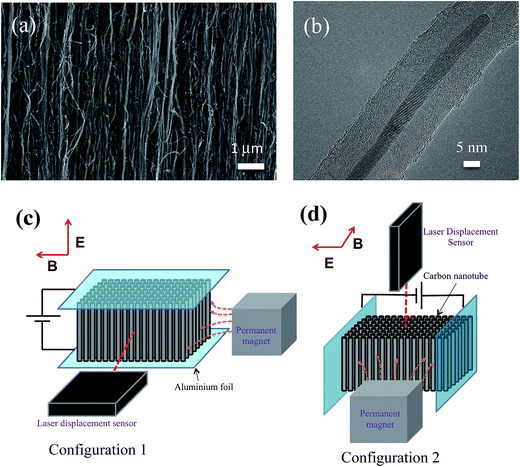
Vertically aligned CNT were grown on silicon dioxide substrate using thermal chemical vapor deposition.¹⁷ Height of the as-grown CNTs were ∼1.12 mm with a bulk density of ∼0.305 g cm⁻³. Actuation measurements were performed on CNT samples of ∼2.74 mm length and width of ∼3.6 mm. Micrograph of the vertically aligned CNTs is shown in Fig. 1a, which reveals an entangled microstructure of CNT despite uniaxial orientation along its axial direction. Fig. 1b reveals transmission electron microscopic (TEM) image of a CNT selected from the bulk CNT, which shows concentric graphitic walls in multiwalled carbon nanotubes (MWCNT). It should also be noted that during the growth of CNT, iron particles adhered to the surface¹⁷ and also get filled inside the core of the CNT as revealed in the Fig. 1b. Because of the high aspect ratio, the bulk structure of CNT presents two working axes as axial and radial, which are along the length and radius of CNT, respectively.

Fig. 1 (a) Microstructure of vertically aligned CNT (cross sectional view). (b) TEM image of an iron filled CNT. (c) Schematic of the experimental setup showing the actuation measurement along the radial direction and (d) axial direction. The respective direction of electric and magnetic fields is demonstrated in the inset.

Displacement of CNT was measured when a voltage (voltage ranges from −0.5 to 0.5 V a step of 0.1 V) was applied using a source and a measurement unit (Keithley 2602A); along with a constant magnetic field (∼0.1 T) applied using a permanent bar magnet. Fig. 1c and d show schematics of the experimental setup used to conduct the actuation experiments along the axial and radial directions, respectively. Directions of electric and the magnetic fields are indicated in the left insets of the schematic shown in Fig. 1c and d. The induced actuation is measured using high-resolution laser displacement sensor (Opto NCDT 2220) with a spot size of ∼60 μm. Electrical contacts across the sample were provided using a very thin aluminium foil (which also acts as a flexible electrode), adhered to the CNT surfaces using a conductive epoxy. Electric field was applied along the axial (configuration 1) and radial directions of CNT (configuration 2) as revealed in Fig. 1c and d, respectively and magnetic field was applied as shown in the schematics. Both the fields were coupled by applying electric field in the perpendicular direction to the external magnetic field. It should be noted that the bar magnet was placed at a constant position throughout the experiments, while both electric field and sample orientation were varied. All the experiments were carried out without varying the direction of magnetic poles. In this study, since magnetic field was not varied hence any actuation due to the variation in the magnetic field is not accounted. Resulting actuation was measured in both the configurations in the perpendicular direction of both the fields as shown in the schematic.

3. Results and discussion

3.1. Actuation induced by electric field alone

The actuation response of CNTs driven by the incurred electric field (without applying magnetic field) for the sample configuration 1 is illustrated in Fig. 2a and b. Experimental observations were made for both positive and negative polarities of the applied voltages. Polarity independent actuation of the CNT forest was recorded upon application of a cyclic voltage (±0.4 V) with a time-period of 10 seconds.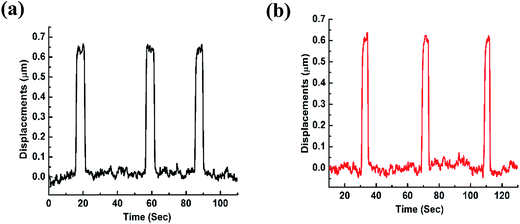

Fig. 2 CNT displacement is plotted with time to illustrate the actuation behavior exhibited by the bulk CNT in response to an external electric field of (a) 0.4 V and (b) −0.4 V.

Responses to both the positive and negative voltages reveal a constant magnitude of actuation (0.65 μm) for all repetitive cycles of applied voltage. Similar behavior of electric field polarity independent behavior of CNT was also observed in earlier studies.^7,18 These studies demonstrated an even functional relationship of the induced strain with the applied electric field, thus projecting CNTs as an electrostrictive material.^6,7,18,19 The mechanism involved in electrostrictive behavior is the asymmetrical elongation of the C–C bond resulting in the modification of its hexagonal ring structure.¹⁹ The current carried by MWCNT is because of the outermost shell, whereas the inner shells doesn't contribute to the current flow.²⁰ In the presence of the electric field the inner tubes get polarized which induces the actuation in these structures.²¹ Thus actuation phenomena in our sample can be explained through the electrostatic Columbic interaction between the individual charge-polarized carbon atoms that triggers an elastic micro-displacement of the bulk CNT structure.^7,19

3.2. Actuation under coupled electric and magnetic fields

Coupled electric and magnetic fields induce an enhanced actuation in the bulk CNT (Fig. 3) as compared to the electric field alone. An external magnetic field was applied orthogonally to both the CNT axis and the applied electric field as shown in Fig. 1c (configuration 1). Resulting displacement of the CNTs in response to the coupled field was several times higher than the displacement recorded in the presence of electric field alone. It is clear that such an amplified displacement response is a consequence of the synergistic effect of the external driving forces generated from both electric and magnetic fields. This enhanced displacement of the bulk CNT could be due to the significant charge polarization along its circumference driven by Lorentz force, which has been illustrated by the schematic shown in Fig. 3a. The extent of this unsymmetrical distribution of the charges along the surface of the nanotubes depends on the relative alignment of the two fields. Similar to the mechanism derived for the electro-mechanical actuation exhibited by the CNTs, actuation driven by these mutually perpendicular fields can be attributed to the dipole-like configuration attained by the separation of the charges.²²

Fig. 3 (a) Actuation mechanism of a CNT under an electro-magnetic field. Arrow indicates the direction of the induced dipole configuration. (b) Displacement in the bulk CNT recorded against time in the presence of external electro-magnetic field for a range of applied voltages (0.1 to 0.5 V) for both the positive (c) negative polarities.

The magnetic field brings about a more pronounced redistribution of the charges (due to the Lorentz force experienced by the electrons) and hence these CNTs experience an enhanced torque at its center. The resulting torque experienced by the bulk CNT comprises of two mutually exclusive components; one involving a torque generated by the external magnetic field,²² while the other relates to the torque generated by the induced electric dipole in response to the applied electric field. When the direction of both of these driving forces coincides, CNTs experience larger force and hence show an enhanced displacement along the specific direction. However, the direction of the induced torque, which is responsible for the actuation in the CNT can be calculated from the vector analysis. A mathematical model has been developed to explain this enhanced actuation response of the bulk CNT structure. As discussed above, the resulting torque, τ_net can be expressed as vector equation:

[small tau, Greek, vector]_net = [small tau, Greek, vector]_EF + [small tau, Greek, vector]_MF (1)

where, the subscripts denote the respective driving fields i.e. electric and magnetic fields, respectively. The mathematical formulation for the actuation induced by the electric field, E alone can be designated by [small tau, Greek, vector]_EF = p⃑ × E⃑, where p is (∑q_ir_i), q_i and r_i denote the individual charges and the distances between them. However, in the presence of the magnetic field, CNTs tend to reduce their potential energy by aligning themselves along the applied field. This can be mathematically formulated as [small tau, Greek, vector]_MF = [small mu, Greek, vector] × B⃑. Thus, eqn (1) can be redefined as:

[small tau, Greek, vector] = p⃑ × E⃑ + [small mu, Greek, vector] × B⃑ (2)

As mentioned-above, this relation demonstrates that due to the synergistic effect of the deforming forces, an enhanced actuation was observed in bulk CNTs. Thermal actuation of the CNT can be ruled out owing to the small-applied bias voltage (±0.5 V) and excellent thermal dissipative properties of CNT.¹

3.2.1. Mathematical modeling of the actuation induced in bulk CNTs. CNT strands were considered as a beam hence, Euler's beam theory can be applied to calculate the net torque acting on the nanotubes. Individual torque due to the electric and the magnetic fields were calculated according to eqn (2), which are responsible for the bending moment acting on the individual CNT beams. 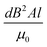The anisotropic MWCNT were considered to have a large effective diameter (its outer and the inner diameters as 100 nm and 60 nm, respectively) hence, net effective susceptibility is approximately |χ_‖ − χ_⊥|.²⁴ Thus, the torque induced by the magnetic field alone can be calculated by applying the formula, , where d is the effective diameter of the nanotubes, B the magnetic field, Al = V, being the volume of the individual CNT strands and μ₀ as the permittivity of free space. Thus, the calculated value of magnetic field induced torque is 17.92 × 10⁻²² N m. Similarly, the calculated torque due to the electric field is 1.25 × 10⁻²³ N m at an applied voltage of 0.5 V. Since the torque induced by the electric and the magnetic fields are either parallel or anti-parallel to each other, the net torque acting on the individual strand is quantified as a summation or a difference of the two. Hence, the net torque acting on CNT is 1.8 × 10⁻²¹ N m, when all the torques are in the same direction. Resulting induced actuation was calculated to be ∼3 μm, which is comparable to the experimentally obtained value of ∼4 μm at 0.5 V. The difference between the theoretical and the experimental values could be due to the attractive van der Waal's force between CNT as well as magnetic field due to the applied voltage, which is not considered for quantitative modeling.

3.3. Polarity dependent actuation under different applied electric field

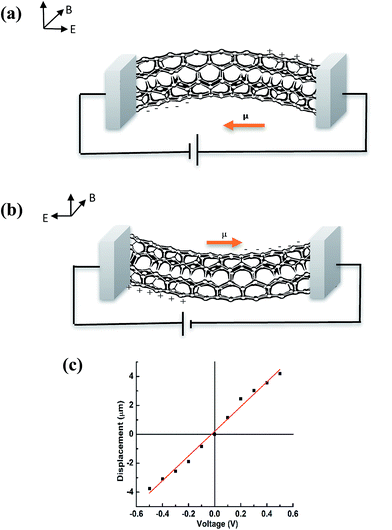
Another striking feature observed in our experiments was a polarity-dependent actuation under the coupled field, which was in direct contrast to the response measured with the electric field only.⁷ This polarity dependent actuation of the CNT structure can be observed in the displacement–time graph, as illustrated in Fig. 3b and c. The magnitude of actuation is shown to increase with the increase in the electric field (applied voltage). It is clear from the figures that the coupled-field imparts a directional actuation to the CNT strands, depending on the polarity of the applied electric field. This could be due to the magnetic anisotropy in the individual CNT as mentioned in several reports,^23,25,26 which arises due to the presence of magnetic particles as also shown in Fig. 1b. Structural anisotropy of the CNTs accounts for their distinct magnetic characteristics.²⁷ Quasi one-dimensional structure of CNT is responsible for their unique magnetic properties such as susceptibility, permeability and their retentivity.^28,29 Similar to other anisotropic materials, CNTs also have shown to align their magnetic dipole and hence their magnetization is aligned along their easy axis.^26,29,30 In the presence of magnetic field, this easy axis coincides with the structural axis of the constricted CNT bulk sample.³⁰ In addition to the alignment, CNTs also undergo a transition from paramagnetic to diamagnetic characteristics depending on the relative alignment of the magnetic field to its axis.^31,32

Fig. 4a and b illustrate the electric field polarity dependent actuation while keeping the direction of the magnetic field constant. On performing the experiment according to the configuration shown in Fig. 4b, reversal of the direction of actuation can be seen upon changing the polarity of the applied voltage. This can be explained by the change in the magnetization of a ferromagnetic material in response to the reversal of the electric current. CNTs in the bulk structure consisted of iron particles, as was evident from the TEM image shown in Fig. 1b and hence, the current flowing through these nanotubes can be considered as spin-polarized. This spin polarized current exerts a torque on the magnetization by transferring the spin angular momentum from the current to the ferromagnetic iron particles.²⁹ A reversal in the direction of this spin polarized current causes a change in the electron spin angular momentum. This ultimately leads to a torque on the magnetization and switches its direction, as illustrated by previous reports.²⁹ A change in the magnetization results in a torque in the opposite direction, which is induced by the magnetic field. Since the torque due to the magnetic field is predominant over its counterpart induced by the electric field, as supported quantitatively earlier, the net torque forces the CNTs to actuate in the opposite direction.²⁹ Similar effect can also be observed with the change in magnetic polarity (south (S) and north (N)). A preliminary result is demonstrated in the ESI† using a solenoid (0.005 T), however a detailed analysis is further required.

Fig. 4 Schematics of the CNT actuation with opposite polarities (a) and (b) of the applied electric field. (c) Displacement of the bulk CNT plotted against the applied voltage for the configuration 1.

From the schematics shown in Fig. 4a and b, it can be clearly seen that in the presence of two fields, the direction of the torque induced by the electric field was dependent on the polarity. This can be related to the reversal of the direction of the magnetic moment driven by the switching of polarity of the applied electric field. This change in the direction of the magnetic moment gives rise to the polarity-dependent actuation of the bulk CNT under the mutually perpendicular fields. Thus the net driving torque acting on these CNTs can be represented by the eqn (2). On correlating the above equation with the schematics in Fig. 4a and b along with the displacement–voltage graphs, we can conclude that the torque generated by the magnetic field dominates the direction of the net torque acting on the CNT strands.

Moreover, the presence of two fields induces a different relationship between the induced strain in CNT and the polarity of the applied voltage, as depicted from the displacement–voltage graph in Fig. 4c. This actuation behavior is in contrast to earlier observed electrostrictive nature of CNT in the presence of electric field alone. Unlike the electro-mechanical actuation, which was dominated by the Columbic interactions,⁷ the displacement brought about by the mutually perpendicular fields was subjected to a torque generated by the induced magnetic and electric dipoles. This net torque, which is acting on the individual nanotubes, is directly dependent on the induced charge, as opposed to the squared power of the charges involved in the Columbic interactions associated with electro-mechanical actuation.

3.4. Comparison of the axial and radial actuation

In addition to the above observations, differences in the actuation responses exhibited by the bulk CNTs under different configurations were also studied. In order to avoid any ambiguity, we shall henceforth term the configuration having the electric current flowing radially, as axial actuation. The configuration having the electric field along the axial direction of the CNTs is termed as the radial actuation. Such a configuration has been illustrated in the schematics shown in Fig. 1c and d and the respective actuation is shown in Fig. 5a and b, respectively.

Fig. 5 (a) Unequal separation of charges along the radial direction of the CNT leading to an enhanced actuation under the configuration of axial actuation. (b) Charge separation along the axial direction of the CNT under the configuration of radial actuation. Displacement plotted against time for (c) axial (d) radial actuations. Arrows indicate the direction of the induced torque.

A higher displacement was recorded in case of the radial actuation, which is presented by Fig. 5c. In the case of radial actuation, the polarization of the charges takes place along the radius of the nanotube, and hence Columbic forces of attraction also come into play. Conversely, the axial actuation configuration involved the separation of the charges by comparatively large distances, resulting in reduced Columbic interactions.

4. Conclusion

In conclusion, a five times higher actuation of bulk CNT structures was demonstrated by coupling both the electric and magnetic fields. Strikingly, the actuation was found to be dependent on the polarity of the applied voltage in the presence of magnetic field as opposed to the polarity independence with the electric field alone. A charge separation scheme is presented to be responsible for the high actuation as well as its polarity dependence. The enhanced actuation of the CNT can be used in the field of biotechnology to solve many health related issues such as liposome mediated gene transfer, have proven to be efficient enough to cure genetic disorders and cancer. Incorporation of such CNT strands into these liposomes may serve as a flagella and aid in their mobility to the target sites, guided by an external magnetic field.

References

1. Q. Liu, W. Ren, F. Li, H. Cong and H.-M. Cheng, J. Phys. Chem. C, 2007, 111, 5006.
2. M. P. Anantram, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, R4837.
3. C. Li, E. T. Thostenson and T.-W. Chou, Compos. Sci. Technol., 2008, 68, 1227.
4. A. O'Halloran, F. O'Malley and P. McHugh, J. Appl. Phys., 2008, 104, 071101.
5. R. H. Baughman, C. X. Cui, A. A. Zakhidov, Z. Iqbal, J. N. Barisci, G. M. Spinks, G. G. Wallace, A. Mazzoldi, D. D. Rossi, A. G. Rinzler, O. Jaschinski, S. Roth and M. Kertesz, Science, 1999, 284, 1340.
6. I.-W. P. Chen, Z. Liang, B. Wang and C. Zhang, Carbon, 2010, 48, 1064.
7. P. Gowda, P. Kumar, R. Tripathi and A. Misra, Carbon, 2014, 67, 546.
8. S. Mallakpour and S. Soltanian, J. Polym. Res., 2014, 21, 553.
9. M. Tahhan, V. Truong, G. M. Spinks and G. G. Wallace, Smart Mater. Struct., 2003, 12, 626.
10. B. J. Alemán, A. Sussman, W. Mickelson and A. Zettl, J. Phys.: Conf. Ser., 2011, 302, 12001.
11. T. Wang and Y. Zhou, Int. J. Solids Struct., 2013, 50, 2970.
12. D. H. Wu, W. T. Chien, C. J. Yang and Y. T. Yen, Sens. Actuators, A, 2005, 118, 171.
13. A. Suri and A. Misra, Nanotechnology, 2013, 24, 105501.
14. P. Jagtap, P. Gowda, B. Das and P. Kumar, Carbon, 2013, 60, 169.
15. A. Pályi, P. R. Struck, M. Rudner, K. Flensberg and G. Burkard, Phys. Rev. Lett., 2012, 108, 206811.
16. Y. Aharonov and D. Bohm, Phys. Rev., 1959, 115, 485.
17. S. K. Reddy, A. Suri and A. Misra, Appl. Phys. Lett., 2013, 102, 241919.
18. K. El-Hami and K. Matsushige, Ultramicroscopy, 2005, 105, 143.
19. W. Guo and Y. Guo, Phys. Rev. Lett., 2003, 91, 115501.
20. P. G. Collins, M. S. Arnold and P. Avouris, Science, 2001, 292, 706.
21. A. Misra and P. Kumar, Nanoscale, 2014, 6, 13668.
22. Z. Wang and L. Philippe, Phys. Rev. Lett., 2009, 102, 215501.
23. M. A. L. Marques, M. d'Avezac and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 125433.
24. S. Zaric, G. N. Ostojic, V. C. Moore, R. H. Hauge, J. Kono, J. Shaver, R. E. Smalley and X. Wei, Nano Lett., 2004, 4, 2219.
25. K. Lakoubovskii, Cent. Eur. J. Phys., 2009, 7, 645.
26. T. Panczyk, M. Drach, P. Szabelski and A. Jagusiak, J. Phys. Chem. C, 2012, 116, 26091.
27. A. V. Okotrub, L. G. Bulusheva, A. G. Kudashov, V. V. Belavin and S. V. Komogortsev, Nanotechnol. Russ., 2008, 3, 191.
28. B. K. Jang, Y. Sakka and S. K. Woo, J. Phys.: Conf. Ser., 2009, 156, 012005.
29. A. Brataas, A. D. Kent and H. Ohno, Nat. Mater., 2012, 11, 372.
30. F. Munoz, J. Mejia-Lopez, T. Perez-Acle and A. H. Romero, ACS Nano, 2010, 4, 2883.
31. J. Ping Lu, Phys. Rev. Lett., 1995, 74, 1123.
32. K. J. Sun, R. A. Wincheski and C. Park, J. Appl. Phys., 2008, 103, 023908.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra01174d

---