View PDF VersionPrevious ArticleNext Article
 
DOI: 10.1039/C5RA00818B (Paper) RSC Adv., 2015, 5, 21823-21830

Structure, stability and intramolecular interaction of M(N5)2 (M = Mg, Ca, Sr and Ba) : a theoretical study†

Xueli Zhang, Junqing Yang, Ming Lu and Xuedong Gong*
School of Chemical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China. E-mail: gongxd325@mail.njust.edu.cn

Received 14th January 2015 , Accepted 17th February 2015

First published on 17th February 2015

Abstract

The potential energetic materials, alkaline earth metal complexes of the pentazole anion (M(N5)2, M = Mg2+, Ca2+, Sr2+ and Ba2+), were studied using the density functional theory. The stable conformation, stability, and pyrolysis mechanism of these complexes were predicted. Dissociation of the title complexes consists of sequential breaking of two N5 rings and the required activation energies (Ea,1, Ea,2 in kJ mol−1) increase in the order of Mg(N5)2 (97.7, 99.9) < Ca(N5)2 (102.3, 104.0) < Sr(N5)2 (105.2, 106.1) < Ba(N5)2 (106.9, 108.8). The small magnitudes (10−7 to 10−4) of the reaction rates show that the dissociation reactions of two N5 rings are very slow. Less electron transfer between the N5 ring and the metal, stronger covalent bonding interactions, and stronger dispersion interactions are responsible for the more stable complexes. The negative change in the enthalpy of dissociation reaction and the acceptable stability illustrate that these complexes may be used as high energy materials.

1. Introduction

In recent years, polynitrogen and nitrogen-rich compounds have attracted a lot of attention.1–12 The fundamental significance of these molecules is their potential as high energy density materials (HEDMs) that are environmentally acceptable. However, the high endothermic heats of formation make the safe synthesis and handling of these molecules the major challenges for experimental chemists. The successful syntheses of the stable salts with N5+ (ref. 13) and the discovery of the metastable N4 with a lifetime exceeding 1 μs at 298 K (ref. 14) have inspired many research groups to search for other stable polynitrogen species. Östmark et al.15 and Vij et al.16 discovered the decomposition of the central C–N bond which connects the aryl and pentazole rings. And they found that N5− exists in gas phase from high-energy mass spectrometric degradation of arylpentazoles.

A large amount of metal salts of N3−, such as Pb(N3)2,17 Zn(N3)2 (ref. 18) and Hg(N3)2,19 have been synthesized. Some of the azido complexes are used as explosives.20–23 The N5− is an analogous full nitrogen anion of N3− with an acceptable stability (decomposition activation energy Ea = 113.0 kJ mol−1).24 Like N3−, N5− can combine with metal cations to form salts. Lein et al.25 and Tang et al.26 proposed that metal can stabilize N5−, which shows a great promise for bulk synthesis of new stable nitrogen-rich compounds with N5−. Significant interests have been shown in the investigation on combination of N5− and metal cations. Various properties of diverse metallic complexes of N5− have been investigated. Glukhovtsev et al.27 reported the structure and stability of LiN5. Many studies28–32 reported the stability of metallic salts with N5−. The strong bonding interactions of Fe(η5-N5)2 with D5d symmetry were investigated by Lein et al.25 The kinetic stabilities of MN5 (M = Li+, Na+, K+ and Rb+)33 and MN5+ (M = Mg2+, Ca2+, Sr2+ and Ba2+) were studied.34 Zhang et al.31 researched the structures, dissociation enthalpies and aromaticities of M2(ηn-N5)2 (M = Be+, Mg+; n = 1, 2) and Ca2(ηn-N5)2 (n = 2, 5). In addition, the equilibrium geometries, thermochemistry and bonding interactions of Ir2(N5)4,26,35 stability and pyrolysis mechanism of Ni(N5)2,36 and the potential use of HB(N5)3M1–2(N5)3BH (M = Be, Mg, Ca, Zn, and Cd) have been reported, too. Though substantial metallic complexes including M2(ηn-N5)2 (M = Mg+ and Ca+, n = 1, 2 or 5) and MN5+ (M = Mg2+, Ca2+, Sr2+ and Ba2+) have been researched, the typical M(N5)2 complexes formed by the alkaline-earth metal cations (Mg2+, Ca2+, Sr2+ and Ba2+) and N5− have not been reported until now. These complexes are supposed to be bounded by electrostatic interaction, covalent bonding interaction and van der Waals interaction. So intramolecular interactions greatly affect the stability of complexes. However, intramolecular interactions of the metallic complexes of N5− have been rarely reported and the relationship between stability and intramolecular interactions has not been reported, too. In this paper, the conformation, pyrolysis mechanism and stability of M(N5)2 (M = Mg2+, Ca2+, Sr2+ and Ba2+) were studied. The relationship between the stability and intramolecular interactions of these complexes were also revealed. The potentials of these complexes as high energy materials were assessed.

2. Computational details

Geometry optimizations of the starting structures (Fig. 1) of four title complexes were carried out at the M06-2X/gen level with the 6-311++G** basis set for N and Lanl2dz for metal which is widely used for the alkaline earth metal complexes.37–40 In addition, G3MP2 was employed to study the conformations of Mg(N5)2 and Ca(N5)2, too. These geometry optimizations were carried out using the Gaussian program package.41 The optimized structures of complexes were confirmed to be local minima without imaginary frequencies. Single point energies of stable structures of four complexes were evaluated at the MP2/gen and MP4/gen levels.
image file: c5ra00818b-f1.tif
Fig. 1 Starting structures of M(N5)2 (M = Mg2+, Ca2+, Sr2+ and Ba2+).

The simulated N–N bond breaking processes in our previous studies42,43 show that the transition state (TS) generally appears when two breaking N–N bond lengths are about 1.70 Å. So the structures with the bond (1) and bond (3) (in Fig. 2) being lengthened to 1.7 Å were built as the starting structures of the transition state optimization at the M06-2X/gen level. The optimized TSs were confirmed by only one imaginary frequency.


image file: c5ra00818b-f2.tif
Fig. 2 Most stable structures of complexes (bond lengths in Å).

Changes in enthalpy and free energy (ΔHs and ΔGs) of the decomposition reactions at 298.15 K were obtained by eqn (1) and (2):

 
ΔH = ∑HP − ∑HR (1)
 
ΔG = ∑GP − ∑GR (2)
∑HP and ∑HR represent the sums of enthalpies of products and reactants in the decomposition reactions, respectively. ∑GP and ∑GR are the corresponding items of free energies.

Activation energy (Ea) was calculated from the total energies of the transition state (ETS) and reactant (ER) using the eqn (3)

 
Ea = ETS − ER (3)

The wavefunction files (.wfn) produced by the Gaussian program were used as inputs for Multiwfn44 to perform the QTAIM (Quantum Theory of Atoms in Molecules) analysis and topological analysis of the electron density distribution. The characteristics of the bond critical point (BCP, denoted as (3, −1)) were obtained in terms of the electron density (ρCP), the Laplacian (∇2ρ) of ρCP, and the total electron energy density (HBCP).

The output files generated by the Gaussian program were used as the inputs for Multiwfn to carry out the charge decomposition analysis (CDA).45 The net transferred charge (qi,j) between fragments i and j was obtained using eqn (4):

 
qi,j = d − b (4)
where d represents the transferred electron from fragment i to fragment j, b indicates the transferred electron from fragment j to fragment i.

3. Results and discussion

3.1 Structure

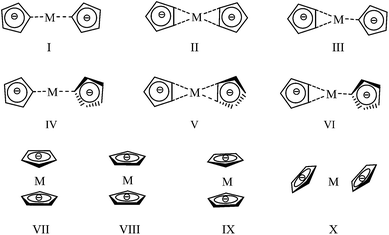
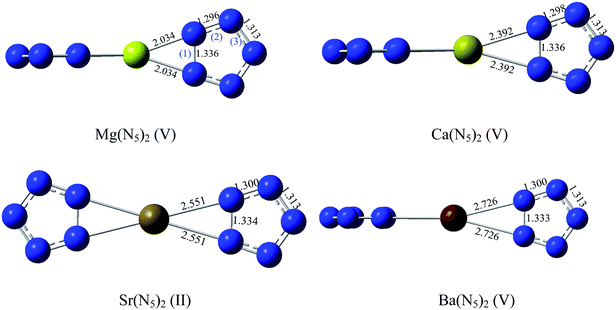
The conformations of metallic complexes of N5− are diverse when the metal cations are different. Ten starting structures (in Fig. 1) which were built based on the previous investigations46 and the characteristics of these complexes were optimized to search for the stable conformations. In I–III, two N5 rings are coplanar and their connections are M(η-N5)2, M(η2-N5)2 and (η2-N5)M(η-N5) respectively. In IV–VI, two N5 rings are perpendicular. The structures VII–IX are analogous to that of ferrocene, among which VII is anti centrosymmetric, VIII is centrosymmetric, while IX is asymmetric. The structure X is randomly built.

Torsional deformation occurred during optimizations of some starting structures. Taking Mg(N5)2 as example, the starting conformation II twisted to V (cf. Fig. 2), VII ultimately changed into II, the configurations VIII and IX transformed to V, and X finally turned into the conformation VI. Geometry optimization finally leads to six stable structures for Mg(N5)2 (I, II, III, IV, V, and VI) and five stable structures for Ca(N5)2, Sr(N5)2, and Ba(N5)2 (II, V, VII, VIII, and IX). To find the most stable conformation among six or five stable structures, the single point energies (Es) of these optimized conformations were calculated at the MP2/gen and MP4/gen levels, and results are listed in Tables S1 and S2 as ESI,† respectively. The results show that the most stable conformation of Mg(N5)2, Ca(N5)2, and Ba(N5)2 is V with the D2d symmetry, this conclusion agrees with the results of Burke et al.46 The most stable configuration of Sr(N5)2 is II with the D2h symmetry. These stable conformations are shown in Fig. 2, together with the measured bond lengths.

In addition, high-level calculations of G3MP2 which gives results comparing well with experiments47 were performed on Mg(N5)2 and Ca(N5)2 to test the reliability of the methods we used. After geometry optimizations of ten starting structures of Mg(N5)2 and Ca(N5)2, only V and VII survive. And the total energy of V (−746.44062 and −1223.92966 a.u. for Mg(N5)2 and Ca(N5)2, respectively) is lower than the corresponding one of VII (−746.38090 and −1223.90575 a.u.), that is, the conformation V should be the most stable structure for Mg(N5)2 and Ca(N5)2 which is in agreement with the results of MP2 and MP4.

As is evident from Fig. 2, the distances between the metal cation and N atoms gradually elongate from 2.034 to 2.726 Å with the increasing atomic number of the metal. Previous studies2–5 reveal that bond (1) and bond (3) of N5 (cf. Fig. 2) easily break, which means that the N5 ring is easy to decompose. Therefore, the stabilities of these bonds are the crucial indexes that reflect the stability of the complexes with the N5 ring. It is well known that the bond length basically reflects the bond stability. Fig. 2 shows that the length of bond (1) decreases in the order of Mg(N5)2 = Ca(N5)2 > Sr(N5)2 > Ba(N5)2, and the lengths of bond (3) are the same. Ba(N5)2 possesses the shortest bond (1), Sr(N5)2 has the second shortest one, bonds (1) and (3) of Mg(N5)2 and Ca(N5)2 are comparable. According to the N–N bond lengths, decomposition of the N5 ring of Ba(N5)2 is supposed to be the hardest, i.e., Ba(N5)2 should be the most stable complex, Sr(N5)2 should be the next most stable one, the stabilities of Mg(N5)2 and Ca(N5)2 should be close.

3.2 Dissociation and stability

Substantial research15,33,36,48,49 has shown that the pyrolysis mechanism of the metallic complexes of N5− is mainly composed of the N5 ring breaking. The title complexes are formed by two N5 anions and one alkaline earth metal cation, two N5 rings break sequentially on decomposition. For the sake of brevity, only the reactants, TSs and products of the decomposition process (path 1 and path 2) of Mg(N5)2 are presented in Fig. 3, that of other complexes are supplied in ESI Fig. S1.† For path 1, the activation energy (Ea,1) is the difference between the total energies of Mg(N5)2 and TS1. For path 2, the activation energy Ea,2 is the difference between the total energies of MgN5N3 and TS2. These activation energies essentially determine the molecular stability which further affects the synthetic possibility and practical application. Table 1 summarizes the calculated Ea,1s and Ea,2s, and the activation energies of the reverse reactions of path 1 and path 2 (Ea,1′ and Ea,2′).
image file: c5ra00818b-f3.tif
Fig. 3 Decomposition processes of Mg(N5)2.
Table 1 Activation energies (in kJ mol−1) of path 1 and path 2a
  Mg(N5)2 Ca(N5)2 Sr(N5)2 Ba(N5)2
a Ea,1′ and Ea,2′ are the activation energies of the reverse processes of path 1 and path 2, respectively.
Ea,1 97.7 102.3 105.2 106.9
Ea,1′ 238.3 209.2 206.6 202.5
Ea,2 99.9 104.0 106.1 108.8
Ea,2′ 241.0 209.0 203.6 201.7

Activation energies (Ea,1 and Ea,2 in kJ mol−1) gradually increase in the order of Mg(N5)2 (97.7 and 99.9) < Ca(N5)2 (102.3 and 104.0) < Sr(N5)2 (105.2 and 106.1) < Ba(N5)2 (106.9 and 108.8). This order verifies our conjecture about the relative stability deduced from the lengths of bond (1) and bond (3). Ea,2 is larger than the corresponding Ea,1, which means that decomposition of the first N5 ring is helpful for stabilizing the rest N5 ring and the stability of MN5N3 is higher than that of the corresponding M(N5)2. The high nitrogen content and acceptable stability of M(N5) and MN5N3 reveal their potentials as HEDMs. Ea,1′ and Ea,2′ are considerably higher than Ea,1 and Ea,2, and the values of Ea,1′ and Ea,2′ are larger than 200 kJ mol−1, so the reverse processes are hard to happen.

The reaction rate constants (ks) of paths 1 and 2 were assessed at 200–500 K with the KiSThelP program50 according to the transition state theory (TST), and the calculated results are tabulated in Table 2. ks of two paths increase rapidly with improving temperature, namely, high temperature lowers the stability and is not good for syntheses and storages of these complexes. When the temperature is lower than 300 K, ks are far smaller than 1, so dissociations of the N5 rings of M(N5)2 and MN5N3 at low temperature (≤300 K) are slow. Breaking of the second N5 ring is slower than that of the first ring, which can be reflected by the smaller ks of path 2 in comparison with that of path 1. For path 1 and path 2, ks gradually reduce from Mg(N5)2 to Ba(N5)2. According to the energy barriers and the reaction rates, Ba(N5)2 should be the most stable complex, Sr(N5)2 is the next most stable one, Mg(N5)2 should be the most unstable complex.

Table 2 Predicted ks (in s−1) of path 1 and path 2
  200 K 298 K 300 K 400 K 500 K
Path 1 Mg(N5)2 2.29 × 10−13 1.01 × 10−4 1.32 × 10−4 3.70 1.86 × 103
Ca(N5)2 1.84 × 10−14 2.02 × 10−5 2.68 × 10−5 1.19 7.93 × 102
Sr(N5)2 3.04 × 10−15 5.84 × 10−6 7.82 × 10−6 4.64 × 10−1 3.65 × 102
Ba(N5)2 5.31 × 10−16 1.39 × 10−6 1.87 × 10−6 1.29 × 10−1 1.12 × 102
Path 2 Mg(N5)2 6.01 × 10−14 4.04 × 10−5 5.34 × 10−5 1.86 1.06 × 103
Ca(N5)2 3.83 × 10−15 5.48 × 10−6 7.32 × 10−6 3.73 × 10−1 2.68 × 102
Sr(N5)2 1.62 × 10−15 3.69 × 10−6 4.96 × 10−6 3.21 × 10−1 2.66 × 102
Ba(N5)2 1.89 × 10−16 7.05 × 10−7 9.54 × 10−7 7.91 × 10−2 7.62 × 10

3.3 Intramolecular interactions and stability

For title complexes, N5− plays the electron donor while M2+ is the electron acceptor. So they are donor–acceptor complexes. The class of donor–acceptor complexes is usually bounded by the covalent bonding interactions, electrostatic interactions and van der Waals interactions. These interactions may exist simultaneously and are related to the stability. In order to figure out the relationships between these intramolecular interactions and stability, they were evaluated.
3.3.1 Covalent bonding interaction. Electronic structure of the donor–acceptor complex has been the topic of many theoretical studies,51–56 and it can reflect the existence of covalent bonding interaction.52 Detail information about the electronic structure of the title complexes can be available from the topological analysis of the electron density distribution. Fig. 4 shows the contour line diagrams of the Laplacian distribution of the electron density. Since two N5 rings of Mg(N5)2, Ca(N5)2 and Ba(N5)2 are not coplanar, only one ring of these complexes appears in Fig. 4. There is one line connecting one N5 ring and Mg2+ and two lines linking one N5 ring and Ca2+, Sr2+ or Ba2+. These lines indicate the existence of bond paths between the N5 ring and M2+.52
image file: c5ra00818b-f4.tif
Fig. 4 Contour diagram of Laplacian distribution (dash lines indicate charge depletion (∇2ρ > 0), and solid lines indicate charge concentration (∇2ρ < 0). The solid lines connecting the atomic nuclei are the bond paths. The blue points are bond critical points).

The properties of the critical points of the bond connecting M2+ and N5− were obtained by QTAIM analysis and are shown in Table 3. According to the viewpoint57 that the covalent bond has the negative HBCP while the ionic bond and van der Waals interaction have positive HBCP, the bonds connecting M2+ and N5− are covalent. It is worth noting that the absolute values of HBCP of Mg(N5)2 and Ca(N5)2 are very small, reflecting that their covalent bonds are very weak. Although HBCP of Mg(N5)2 (−0.05057 a.u.) is more negative than that of Ca(N5)2 (−0.02956 to −0.02964 a.u.), the latter has two more covalent bonds than the former does, therefore, the total covalent bonding interactions of Ca(N5)2 should be stronger than that of Mg(N5)2. Compared with the HBCPs of Mg(N5)2 and Ca(N5)2, the absolute values of HBCP of Sr(N5)2 (−0.14862 to −0.14879 a.u.) and Ba(N5)2 (−0.18186 to −0.18272 a.u.) are obviously larger. Therefore, the covalent bonding interactions of Sr(N5)2 and Ba(N5)2 are stronger than that of Mg(N5)2 and Ca(N5)2. However, the covalent bonding interactions of Sr(N5)2 and Ba(N5)2 are obviously weaker than that of the typical covalent bonding complexes NH3BH3 (−0.35 a.u.) and N(CH3)3BH3 (−0.44 a.u.),52 which means that the title complexes are not the typical covalent bonding complexes. In addition, the electron density (ρCP) located at the critical point and its ∇2ρ essentially improve with the increasing atomic number of metal. It can be concluded that covalent bonding interactions should decrease in the order of Ba(N5)2 > Sr(N5)2 > Ca(N5)2 > Mg(N5)2. This order is the same to that of stability, that is, the stronger covalent bonding interaction corresponds to the more stable complex.

Table 3 Electron density (ρCP), Lapacian electronic density (∇2ρ) and energy density (HBCP)
Complex ρCP (a.u.) ∇2ρ (a.u.) HBCP (a.u.)
Mg(N5)2 0.09461 0.16836 −0.05057
0.09461 0.16837 −0.05057
Ca(N5)2 0.06723 0.17298 −0.02961
0.06710 0.17239 −0.02956
0.06732 0.17327 −0.02969
0.06724 0.17326 −0.02964
Sr(N5)2 0.15937 0.16616 −0.14862
0.15920 0.15572 −0.14874
0.15878 0.13985 −0.14873
0.15922 0.15605 −0.14879
Ba(N5)2 0.17298 0.37385 −0.17971
0.17310 0.37276 −0.17990
0.13111 0.37294 −0.17995
0.17288 0.37499 −0.17945

3.3.2 Electrostatic interaction. The title complexes are composed of M2+ and N5−, so the existences of electrostatic interaction and electron transfer between cation and anion should be chemically intuitive. The larger absolute values of the charges on the cation and anion are beneficial to resulting in the stronger electrostatic interactions. The electron transfer between the N5 ring and metal changes the charges of ions which further affect the strengths of electrostatic interactions. Therefore, the electron transfer was investigated by the charge decomposition analysis (CDA).45 In the CDA calculations, two N5 rings and metal cation were defined as fragment 1, fragment 2 and fragment 3, respectively. Results are tabulated in Table 4.
Table 4 Transferred electrons between N5 rings and metal (q1,3 and q2,3), total transferred electrons (qt), and charges on N5 rings and metal (Q1, Q2 and Q3)
  Mg(N5)2 Ca(N5)2 Sr(N5)2 Ba(N5)2
q1,3 (e) 0.252 0.171 0.146 0.123
q2,3 (e) 0.252 0.171 0.146 0.123
qt (e) 0.504 0.342 0.292 0.246
Q1 (e) −0.748 −0.829 −0.854 −0.877
Q2 (e) −0.748 −0.829 −0.854 −0.877
Q3 (e) 1.496 1.658 1.708 1.754

Basically no electron transfers from M2+ to N5−, which is in line with the chemical intuition. The same values of q1,3 and q2,3 reveal that the transferred electrons from two N5 rings to metal cation are equal, which certainly results in the same charges on two N5 rings (Q1 and Q2). The total transferred electrons from N5 rings to metal cation (qt) gradually decrease in the order of Mg(N5)2 > Ca(N5)2 > Sr(N5)2 > Ba(N5)2. The smaller qt corresponds to the more charges on metal (Q3) and N5 ring. The absolute values of Q1, Q2 and Q3 increase in the order of Mg(N5)2 < Ca(N5)2 < Sr(N5)2 < Ba(N5)2, which is the same to the variation trend of the stability. This means that the less transferred electrons which correspond to the stronger electrostatic interactions are beneficial to stabilizing the metallic complex. This result agrees with the conclusion obtained in previous research.3,4,7

3.3.3 Dispersion interaction. Dispersion interaction is the important component of van der Waals interaction and can be evaluated using the DFT-D3 procedure. Two N5 rings and metal were also defined as fragment 1, fragment 2 and fragment 3 in the dispersion interaction analysis, respectively. Table 5 shows the calculated results. The dispersion interactions between two N5 rings and metal cation (Edis,1,3 and Edis,2,3) are the same. The comparable HBCPs, the same q1,3 and q2,3, and the same Edis,1,3 and Edis,2,3 reveal that the intramolecular interactions between two N5 rings and the metal are almost identical. Edis,1,3 and Edis,2,3 reduce in the order of Ba(N5)2 > Sr(N5)2 > Ca(N5)2 > Mg(N5)2. Dispersion interaction between two N5 rings (Edis,1,2) is also found, while Edis,1,2 is obviously lower than Edis,1,3 and Edis,2,3. In addition, Edis,1,2 gradually decreases with the increasing atomic number of the metal, which is because the distance between two N5 rings gradually enlarges from Mg(N5)2 to Ba(N5)2 and the longer distance naturally results in the weaker dispersion interaction. Compared to the dispersion interactions between different fragments, the interactions within the N5 ring (Edis,1 and Edis,2) are obviously stronger. Edis,1 and Edis,2 of different complexes are almost the same, which reveals that the different metal cations hardly affect the dispersion interaction within the N5 ring. The total dispersion interactions have the order of Ba(N5)2 > Sr(N5)2 > Ca(N5)2 > Mg(N5)2. This order is the same to that of stability, so the stronger dispersion interaction corresponds to the more stable complex, too.
Table 5 Predicted dispersion interactions (in kJ mol−1)
  Mg(N5)2 Ca(N5)2 Sr(N5)2 Ba(N5)2
Edis,1,3 −10.9 −11.6 −11.8 −12.3
Edis,2,3 −10.9 −11.6 −11.8 −12.3
Edis,1,2 −2.0 −0.8 −0.5 −0.4
Edis,1 or Edis,2 −15.3 −15.3 −15.3 −15.2
Edis,t −54.4 −54.6 −54.7 −55.4

3.4 Enthalpy of decomposition reaction

High energy content is always desired for energetic materials. The more energy the compound releases on explosion, the better detonation performance the compound possesses. Change in enthalpy (ΔH) of decomposition reaction reflects the capacity of a compound to release energy on explosion. The enthalpy of both steps of decomposition of the title complexes was evaluated. Due to the high thermal stability and high nitrogen content of MN5N3, their ΔHs were also predicted to assess their potentials as HEDMs. The calculated results are tabulated in Table 6 and the decomposition reactions are as follows:
M(N5)2 = M + 5N2 (M = Mg, Ca, Sr and Ba)

MN5N3 = M + 4N2 (M = Mg, Ca, Sr and Ba)
Table 6 Predicted ΔH and ΔG (in kJ mol−1) of decomposition reactions of M(N5)2 and MN5N3
Compound ΔH ΔG Compound ΔH ΔG
Mg(N5)2 −267.9 −360.2 MgN5N3 −134.3 −174.3
Ca(N5)2 −198.5 −289.3 CaN5N3 −98.6 −136.8
Sr(N5)2 −186.2 −266.1 SrN5N3 −91.1 −121.4
Ba(N5)2 −175.5 −272.1 BaN5N3 −86.4 −134.9

Since N2 molecule is the most stable form of nitrogen, it is not unexpected that ΔHs of decomposition of M(N5)2 and MN5N3 are negative and title complexes have high energy contents. These results show that M(N5)2 and MN5N3 may be used as highly energetic materials. Compared to MN5N3, M(N5)2 should be the better energetic materials because they release much more energies. The negative change in free energy of decomposition reaction (ΔG) suggests that the dissociations of M(N5)2 and MN5N3 are spontaneous.

4. Conclusion

The complexes formed by the alkaline earth metal and two pentazole anions (M(N5)2, M = Mg2+, Ca2+, Sr2+ and Ba2+) are studied in this work for accessing their potentials as highly energetic materials and revealing the relationship between stability and intramolecular interactions. The most stable conformation is the non-planar tail to tail for Mg(N5)2, Ca(N5)2 and Ba(N5)2, and the planar tail to tail for Sr(N5)2. Two N5 rings break sequentially during decomposition of these complexes, and dissociation of the first ring stabilizes the rest N5 ring. The activation energies and rate constants of the decomposition reactions show that the stabilities of the complexes increase from Mg(N5)2 to Ba(N5)2. Generally, the more stable complex possesses the stronger covalent bonding interactions, electrostatic interactions and dispersion interactions. The acceptable stability and the negative ΔH of decomposition process reveal the potentials of M(N5)2 and MN5N3 as high energy materials.

References

  1. P. K. Swain, J. Mol. Liq., 2010, 157, 1–5 CrossRef CAS PubMed.
  2. G. Frison, G. Jacob and G. Ohanessian, New J. Chem., 2013, 37, 611–618 RSC.
  3. M. Rahm and T. Brinck, Chem.–Eur. J., 2010, 16, 6590–6600 CrossRef CAS PubMed.
  4. P. G. Seybold and W. Kreye, Int. J. Quantum Chem., 2012, 112, 3769–3776 CrossRef CAS.
  5. Y.-c. LI and S.-p. Pang, Chin. J. Explos. Propellants, 2012, 35, 1–8 Search PubMed.
  6. X.-F. Chen, J.-H. Bu, T. Yu, W.-P. Lai and Z.-X. Ge, Communications in Computational Chemistry, 2013, 1, 118–123 Search PubMed.
  7. M. Xu, Q. Pan, Z.-q. Chen, G. Zhang, Y.-l. Ning, M.-c. Wang, M. Wang and F.-q. Bi, Chin. J. Explos. Propellants, 2013, 1, 005 Search PubMed.
  8. M. Xu, F.-q. Bi, G. Zhang, M.-c. Wang, Z.-x. Ge, Z.-q. Chen and C. Xu, Chin. J. Energ. Mater., 2012, 5, 031 Search PubMed.
  9. F.-q. Bi, C. Xu, X.-z. Fan, Z.-x. Ge, B.-z. Wang, M.-c. Wang, Q. Liu and M. Xu, Chin. J. Explos. Propellants, 2012, 2, 002 Search PubMed.
  10. U. Geiger, A. Elyashiv, R. Fraenkel, S. Zilberg and Y. Haas, Chem. Phys. Lett., 2013, 556, 127–131 CrossRef CAS PubMed.
  11. P. Portius, M. Davis, R. Campbell, F. Hartl, Q. Zeng, A. J. Meijer and M. Towrie, J. Phys. Chem. A, 2013, 117, 12759–12769 CrossRef CAS PubMed.
  12. U. Geiger, Y. Haas and D. Grinstein, J. Photochem. Photobiol., A, 2014, 277, 53–61 CrossRef CAS PubMed.
  13. K. O. Christe, W. W. Wilson, J. A. Sheehy and J. A. Boatz, Angew. Chem., Int. Ed., 1999, 38, 2004–2009 CrossRef CAS.
  14. F. Cacace, G. d. Petris and A. Troiani, Science, 2002, 295, 480–481 CrossRef CAS PubMed.
  15. H. Östmark, S. Wallin, T. Brinck, P. Carlqvist, R. Claridge, E. Hedlund and L. Yudina, Chem. Phys. Lett., 2003, 379, 539–546 CrossRef PubMed.
  16. A. Vij, J. G. Pavlovich, W. W. Wilson, V. Vij and K. O. Christe, Angew. Chem., 2002, 114, 3177–3180 CrossRef.
  17. E. H. Younk and A. B. Kunz, Int. J. Quantum Chem., 1997, 63, 615–621 CrossRef CAS.
  18. D. Forster and W. D. Horrocks Jr, Inorg. Chem., 1966, 5, 1510–1514 CrossRef CAS.
  19. P. Nockemann, U. Cremer, U. Ruschewitz and G. Meyer, Z. Anorg. Allg. Chem., 2003, 629, 2079–2082 CrossRef CAS.
  20. W. Zhu and H. Xiao, J. Phys. Chem. C, 2011, 115, 20782–20787 CAS.
  21. V. Kriger, A. Kalenskii, A. Zvekov, A. Borovikova and E. Grishaeva, Combust., Explos. Shock Waves, 2012, 48, 488–495 CrossRef.
  22. B. d. Wu, S. w. Wang, L. Yang, T. l. Zhang, J. g. Zhang, Z. n. Zhou and K. b. Yu, Eur. J. Inorg. Chem., 2011, 2011, 2616–2623 CrossRef.
  23. F.-C. Liu, Y.-F. Zeng, J. Jiao, X.-H. Bu, J. Ribas and S. R. Batten, Inorg. Chem., 2006, 45, 2776–2778 CrossRef CAS PubMed.
  24. S. Fau, K. J. Wilson and R. J. Bartlett, J. Phys. Chem. A, 2002, 106, 4639–4644 CrossRef CAS.
  25. M. Lein, J. Frunzke, A. Timoshkin and G. Frenking, Chem.–Eur. J., 2001, 7, 4155–4163 CrossRef CAS.
  26. L. Tang, H. Guo, J. Peng, P. Ning, K. Li, J. Li, J. Gu and Q. Li, J. Organomet. Chem., 2014, 769, 94–99 CrossRef CAS PubMed.
  27. M. N. Glukhovtsev, P. v. R. Schleyer and C. Maerker, J. Phys. Chem., 1993, 97, 8200–8206 CrossRef CAS.
  28. M. Noyman, S. Zilberg and Y. Haas, J. Phys. Chem. A, 2009, 113, 7376–7382 CrossRef CAS PubMed.
  29. P. Carlqvist, H. Östmark and T. Brinck, J. Phys. Chem. A, 2004, 108, 7463–7467 CrossRef CAS.
  30. F. Blanco, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2008, 112, 7582–7688 CrossRef PubMed.
  31. X. H. Zhang, S. Li and Q. S. Li, J. Theor. Comput. Chem., 2006, 05, 475–487 CrossRef.
  32. J. Frunzke, M. Lein and G. Frenking, Organometallics, 2002, 21, 3351–3359 CrossRef CAS.
  33. J. F. Zhao, N. Li and Q. S. Li, Theor. Chem. Acc., 2003, 110, 10–18 CrossRef CAS PubMed.
  34. J. F. Zhao and Q. S. Li, Int. J. Quantum Chem., 2004, 98, 485–494 CrossRef CAS.
  35. L. H. Tang, H. B. Guo, Q. S. Li, J. H. Peng, J. J. Gu and L. B. Xiao, Adv. Mater. Res., 2014, 924, 233–252 CrossRef CAS.
  36. X. Zhang, J. Yang, M. Lu and X. Gong, Theoretical Studies on Stability and Pyrolysis Mechanism of Salts Formed by N5− and Metallic Cations Na+, Fe2+ and Ni2+, Struct. Chem., 2014 DOI:10.1007/s11224-014-0536-x.
  37. S. E. Rodriguez-Cruz, R. A. Jockusch and E. R. Williams, J. Am. Chem. Soc., 1999, 121, 1986–1987 CrossRef CAS PubMed.
  38. C. Zubieta, N. J. Castellani and R. M. Ferullo, Comput. Theor. Chem., 2013, 1009, 1–7 CrossRef CAS PubMed.
  39. J. Heo, Bull. Korean Chem. Soc., 2012, 33, 2669 CrossRef CAS.
  40. M. Peschke, A. T. Blades and P. Kebarle, J. Am. Chem. Soc., 2000, 122, 10440–10449 CrossRef CAS.
  41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J. E. Knox, H. P. Hratchian, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, P. Y. Ayala, K. Morokuma, G. A. Voth, P. Salvador, J. J. Dannenberg, V. G. Zakrzewski, S. Dapprich, A. D. Daniels, M. C. Strain, O. Farkas, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. V. Ortiz, Q. Cui, A. G. Baboul, S. Clifford, J. Cioslowski, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, M. Challacombe, P. M. W. Gill, B. Johnson, W. Chen, M. W. Wong, C. Gonzalez and J. A. Pople, Gaussian 03, Revision C.02, Gaussian, Inc., Wallingford CT, 2004 Search PubMed.
  42. X. Zhang, J. Yang, M. Lu and X. Gong, RSC Adv., 2014, 4, 56095–56101 RSC.
  43. X. Zhang, J. Yang, M. Lu and X. Gong, Struct. Chem., 2014, 1–8 Search PubMed.
  44. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
  45. S. Dapprich and G. Frenking, J. Phys. Chem., 1995, 99, 9352–9362 CrossRef CAS.
  46. L. A. Burke, R. N. Butler and J. C. Stephens, J. Chem. Soc., Perkin Trans. 2, 2001, 1679–1684 RSC.
  47. B. M. Wong, D. Lacina, I. M. Nielsen, J. Graetz and M. D. Allendorf, J. Phys. Chem. C, 2011, 115, 7778–7786 CAS.
  48. V. Benin, P. Kaszynski and G. Radziszewski, J. Org. Chem., 2002, 67, 1354–1358 CrossRef CAS PubMed.
  49. R. N. Butler, J. M. Hanniffy, J. C. Stephens and L. A. Burke, J. Org. Chem., 2008, 73, 1354–1364 CrossRef CAS PubMed.
  50. S. Canneaux, F. Bohr and E. Hénon, J. Comput. Chem., 2014, 35, 82–93 CrossRef CAS PubMed.
  51. E. D. Glendening and A. Streitwieser, J. Chem. Phys., 1994, 100, 2900–2909 CrossRef CAS PubMed.
  52. V. Jonas, G. Frenking and M. T. Reetzi, J. Am. Chem. Soc., 1994, 116, 8741–8753 CrossRef CAS.
  53. N. Cox, M. Retegan, F. Neese, D. A. Pantazis, A. Boussac and W. Lubitz, Science, 2014, 345, 804–808 CrossRef CAS PubMed.
  54. P. A. Clayborne and H. Häkkinen, Phys. Chem. Chem. Phys., 2012, 14, 9311–9316 RSC.
  55. X. Wan, A. M. Turner, A. Vishwanath and S. Y. Savrasov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205101 CrossRef.
  56. N. Bork, L. Du and H. G. Kjaergaard, J. Phys. Chem. A, 2014, 118, 1384–1389 CrossRef CAS PubMed.
  57. D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627–628 CrossRef.

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra00818b
This journal is © The Royal Society of Chemistry 2015
Click here to see how this site uses Cookies. View our privacy policy here.