Effect of a silica nanofiller on the structure, dynamics and thermostability of LDPE in LDPE/silica nanocomposites

Abstract

The effect of the presence of silica nanoparticles on the structure, thermal stability and dynamics of low density polyethylene, LDPE, has been studied. Different loads of nanoparticles were dispersed within a LDPE matrix using high energy ball milling (HEBM) as a preliminary processing step to ensure a uniform dispersion of nanofiller to obtain nanocomposites in the form of films by hot pressing. The monitoring of the FTIR-ATR spectra of the samples as a function of the temperature has proven as a convenient method to study the interactions at a molecular scale between the polyethylene chains and the nanofiller. Band splitting observed in the bending and rocking modes of the ethylene groups indicated formation of crystalline phases whereas the analysis of absorbance band ratios from the stretching vibrations of PE accounted for the behavior of the polymer bulk. No evidence of strong polymer–filler interactions were found with the exception of a thermal relaxation process observed at 55 °C. Structural, morphological and thermal characterization of the nanocomposites did not reveal remarkable changes at low loads of filler, indicating that in the case of LDPE–silica nanocomposites, where weak interactions between the polymer and filler occur, the volume fraction of nanoparticles must be relatively high in order to produce changes in the bulk properties.

---

Introduction

During the past twenty years much effort has been made in understanding the real effect of the incorporation of nanoparticles into polymers to form a nanocomposite material.¹ Changes in the bulk properties of polymers under the influence of nanofillers may have the origin either in the intrinsic features of the nanoparticles (electrical, optical, mechanical) or be ascribed to structural and morphological changes induced in the polymer by the presence of the nanoparticles. In the first case, usually a simple model based on the rule of mixtures can be applied to predict the behaviour of the material. The second one, however, is more difficult to ascertain, as it mainly depends on the specific interactions taking place between the particles and the polymer chains, which in turn are connected to the size and aspect ratio of the particles. Due to the increased surface to volume ratio of nanoparticles there is a large fraction of interphase in a nanocomposite, in which a gradient of physico-chemical properties exists from one phase, the particle, to the other, the polymer, a fact which is going to be decisive in the final properties of the material. Quite often, even small amounts of the nanofiller may produce important consequences on the final properties of the material.²

There is a number of techniques capable of providing information at different levels which can be used in the study of nanocomposite materials³ such as DRX,^4,5 NMR,⁶ FTIR^7,8 for the structure; optical microscopy,⁹ SEM^10–12 and AFM¹³ for the morphology; and DSC¹⁴ and DMTA¹⁵ for the macromolecular dynamics. Particularly, FTIR spectroscopy has been widely used to monitor curing reactions in polymer composites by analysing the bands of different absorbing groups as a function of the curing time with the temperature.^16,17 The use of FTIR spectroscopy with the aid of fluorescence has also allowed the study of processes such as chemical reactions,¹⁸ phase separation¹⁹ or water absorption.²⁰ More recently, the analysis of FTIR-ATR absorption bands has been used to study the changes accompanying interfacial conformations and molecular structure in PMMA–silica nanocomposites.^8,21,22

A factor of paramount importance in the characterization of this type of materials is the uniform dispersion of the nanoparticles within the polymer to avoid effects derived from the potential aggregation of the particles. Thus, different approaches have been described in the literature to achieve a good dispersion of nanoparticles into polymer matrices, such as chemical modification of the surface of the nanoparticles or the polymeric matrices to generate specific functional groups, in situ polymerization, or sol–gel methods to create nanoparticles within the polymer,²³ among other methods. However, when filler loads are usually higher than 5% by weight and for particles with diameters under 50 nm (ref. 24) to achieve a uniform dispersion of the nanofiller proves to be a challenge. A suitable approach, currently used in metallic alloying, is high energy ball milling (HEBM), a method that has been proven to be very effective in dispersing nanofillers in thermoplastic polymers in a fast and clean way.^8,22–28

Within this frame, the aim of this investigation has been to prepare and characterize nanocomposites of LDPE filled with uniformly dispersed SiO₂ nanoparticles in order to understand the influence of the presence of the nanofiller in the structure, morphology, thermodegradation and dynamics of the polymeric matrix. A procedure based on monitoring the evolution of selected ATR bands of the LDPE as a function of temperature that can be applied to other polymeric matrices has been proposed that permits to obtain information at a molecular scale about the structure, specific interactions, and melting process of the semicrystalline polymer under the influence of the silica nanofiller.

Experimental

Materials

Commercial low density polyethylene, LDPE (melt index 25.00 g/10 min, 190 °C/2.16 kg, ASTM D 1238 and 0.93 g cm⁻¹ density) was supplied by Aldrich. Fumed silica nanoparticles (200 m² g⁻¹ surface area, 2.2 g cm⁻³ density, 14 nm of diameter) were supplied by Sigma-Aldrich.

Sample preparation

LDPE and its mixtures with SiO₂ nanoparticles were ground under cryogenic conditions in a mill RESCHT MM 400. 16 mL of the raw materials were introduced into vials with one stainless steel ball (2.5 cm ∅). The vials were then hermetically closed with Teflon spacers and immersed in liquid nitrogen for 15 min prior milling at 28 Hz for 5 minutes. This cycle was repeated until reaching one hour of active milling.

Nanocomposites were prepared in the form of films from the milled mixtures by hot pressing using a Microtest S.A. pressing machine. The milled powders were placed in an aluminium mould sandwiched by two Teflon sheets as anti-adherent. Powders were subjected to a constant load of 20 kN at 150 °C for 8 minutes. Then, the samples were left to cool down at room temperature under the same constant pressure.

Experimental techniques and methods

Thermogravimetric analysis, TGA, was carried out with a thermal analyzer Mettler TGA/SDTA851 with multisampler device. All the samples were measured in 50 μL Pt crucibles under nitrogen atmosphere. To study the kinetics of the thermodegradation process of the nanocomposites different heating rates (10, 15, 20 and 25 °C min⁻¹) were used.

Melting and crystallization processes were monitored using a Mettler Toledo 822e differential scanning calorimeter under nitrogen atmosphere using the following thermal cycle: (i) a dynamic heating step from 35 °C to 150 °C at 10 °C min⁻¹; (ii) an isothermal step at 150 °C for 1 hour; (iii) a dynamic cooling step from 150 °C to 35 °C at 10 °C min⁻¹; (iv) an isothermal step at 35 °C for 3 min; and (v) a dynamic heating step from 35 °C to 150 °C at 10 °C min⁻¹. The experiments were carried out in 40 μL aluminium crucibles.

Morphological characterization of the films was carried out by AFM using a scanning probe microscope MultiMode Nanoscope IVA (Veeco), at ambient conditions in tapping mode with etched silicon probes (40 N m⁻¹). To ensure the same thermal history of all samples, the films underwent exactly the same thermal cycle used for calorimetric studies using the same calorimeter. The DSC crucibles with the samples were then glued on AFM metal discs with epoxy resin. Then the cover of the DSC capsule was carefully removed with a razor blade and subsequently blown with nitrogen to clean the surfaces, prior to AFM visualization.

A Nicolet Avatar 360-Golden Gate Diamond FTIR-ATR with temperature controller was used to study the LDPE and the nanocomposites as a function of temperature. Samples were kept at 140 °C on the diamond of the ATR accessory for one hour to erase the thermal history before recording the IR spectra as a function of temperature. The dynamic experiment was run cooling down from 140 °C to 40 °C at a cooling rate of 50 °C h⁻¹.

Results and discussion

Thermal stability and DSC studies

The mass losses as a function of temperature of the nanocomposites with different SiO₂ contents are shown in Fig. 1 for a heating rate of 10 °C min⁻¹.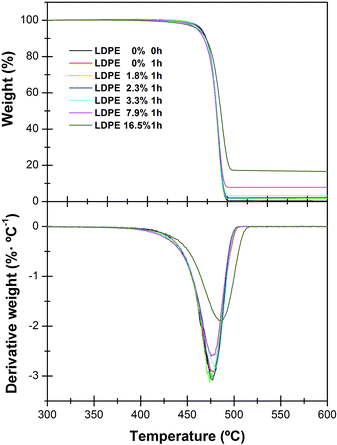

Fig. 1 TGA curves (top) and their derivatives DTGA (bottom) for the neat LDPE and its nanocomposites: LDPE 1.8%; LDPE 2.3%; LDPE 3.3%; LDPE 7.9%; LDPE 16.5% of SiO₂ nanoparticles.

For the rest of the temperature ramps studied similar profiles were obtained, the only difference being the temperature at which the decomposition rate is maximum, T_max, as expected taking into account the kinetic character of the thermal decomposition process. For low loads of nanofiller, the temperature of thermal decomposition, does not change significantly with the content of nanoparticles (T_max = 477 °C, Fig. 1, top). This is better perceived in the first derivative, DTGA plot (Fig. 1, bottom), which shows how the degradation temperature increases significantly only when the amount of silica nanoparticles is high enough, reaching a value of T_max = 486 °C for LDPE filled with 16.5 wt% of SiO₂.

The kinetic study of the process of thermal decomposition has been performed according to the Kissinger's method via the analysis of the TGA curves of the samples at different heating rates.^29,30 Activation energies, E_a, of 270 ± 20 kJ mol⁻¹ were obtained regardless the composition. Similar values have been reported for this polymer in the literature,³¹ which indicates that the presence of nanoparticles has not a noticeable catalytic or inhibiting effect on the decomposition of LDPE. This result evidences no specific interactions between the polar surface of the silica nanoparticles and the non-polar LDPE chains, in accordance to the different chemical nature of both components.

Regarding the calorimetry studies, different parameters obtained from the DSC scans have been considered: the temperature of crystallization obtained at the exothermic peak, T_cp, the average temperature of crystallization, 〈T_c〉, by considering the DSC exothermic peak as a distribution of temperatures, and the degree of crystallization, χ_c. These parameters have been plotted in Fig. 2. Upon cooling, the temperature of crystallization and the degree of crystallization remain virtually constant with the content of SiO₂, although the difference between T_cp and 〈T_c〉 seems to increase with the content of silica. This may indicate that the contribution of a particular crystalline domain increases with the content of particles but without modifying the overall crystallinity of the polymeric matrix, which remains practically constant at a value around 0.45.

Fig. 2 Crystallization temperatures, T_cp and 〈T_c〉, and degree of crystallinity, χ_c, taken from the exothermic peaks in the cooling scans as a function of the content of SiO₂ (the dotted line corresponds to the average value of the degree of crystallinity calculated from all the samples).

Morphological analysis by AFM

Fig. 3 shows the AFM height images obtained for the nanocomposites with different amounts of nanosilica. The non-milled LDPE (LDPE 0h) shows a surface with randomly distributed needle-like structures or lamellae that may correspond to relatively large crystalline domains (spherulites). After milling for 1 h (LDPE 1h) an important contribution of crystalline domains with longer and thinner lamellar structures can be observed. The introduction of silica nanoparticles (LDPE–1.8% SiO₂ 1h) induces additional changes in morphology, more clearly seen in samples LDPE–2.3% SiO₂ and LDPE–3.3% SiO₂, where a third contribution to the crystalline morphology constituted by droplet like structures can be visualized. Finally, for higher loads of nanoparticles (LDPE–7.9% SiO₂ and LDPE–16.5% SiO₂), the morphology corresponding to the milled LDPE without particles seems to be recovered. Therefore, although no significant differences are observed in terms of the degree of crystallinity (Fig. 2, χ_c), AFM points out changes with milling and the presence of nanosilica particles, as reflected in the fine morphology associated to lamellar shape and size.

Fig. 3 Height AFM images for samples with different nanosilica content (scan size is 10 × 10 μm²; color scale 500 nm).

It is also worth mentioning that there is no direct evidence of the presence of the silica nanoparticles on the surfaces of the samples, which suggest that the nanofiller tends to locate in the polymer bulk rather than on the outer surface of the material. In fact, when the samples are ultramicrotomed the presence of silica nanoparticles is clearly evidenced by AFM.¹³

FTIR-ATR

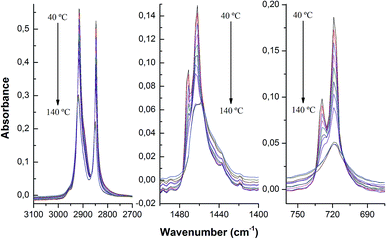
The melting process of LDPE has been followed by FTIR-ATR, trying to visualize at a molecular scale the influence of the presence of silica nanoparticles. Normalized FTIR-ATR spectra recorded at 40 °C and 140 °C are shown in Fig. 4. The spectra show changes occurring in the polymer when cooling from 140 °C (liquid) to 40 °C (solid). Polyethylene chains can be found in essentially two configurations: planar zig-zag, representing the crystalline regions of the polymer,³² and random configuration, only restricted by the conservation of bond angles and distances,³³ which constitutes the amorphous regions. However, the random configuration becomes partially oriented when the sample is stretched³⁴ and therefore, the spectrum of PE is usually represented by a superposition of the spectra arising from two different types of chain configurations.

Fig. 4 FTIR-ATR spectra of the nanocomposites (LDPE; LDPE 1.8%; LDPE 2.3%; LDPE 3.3%; LDPE 7.9%; LDPE 16.5% of SiO₂ nanoparticles) at 40 °C (top) and 140 °C (bottom).

All the spectra show a wide band centered at about 1100 cm⁻¹ that is assigned to the siloxane Si–O–Si bonds of the silica nanoparticles whose absorbance increases as the silica content increases (Fig. 4). It would seem that the temperature is influencing somewhat the absorbance of the Si–O–Si stretching but that apparent increase comes in fact from the normalization to the CH₂ stretching band of the LDPE, which is affected upon melting. As for the PE bands, the most intense ones are the asymmetric, ν_a(CH₂), and symmetric stretching, ν_s(CH₂), modes of the CH₂ group, always present in hydrocarbons and different forms of PE.³⁵ These bands appear in the ATR spectra at 2916 cm⁻¹ and 2847 cm⁻¹, respectively (Fig. 4, top). The bending mode of CH₂ in polyethylene, δ(CH₂), appears at about 1460 cm⁻¹,³⁶ and the rocking mode of the CH₂, γ_r(CH₂), at 725 cm⁻¹. However, band splitting for the rocking and bending modes of methylene can be observed at 720 cm⁻¹ and 1462 cm⁻¹, respectively, (Fig. 4 top), a feature that has been ascribed to the presence of crystalline phases in the PE, as reported by S. Krimm et al.³⁶ These doublets disappear when the temperature of the samples is well above the melting point, at 140 °C (Fig. 4, bottom). There are other significant changes in the spectra when temperature increases: (i) a very small shift of the CH₂ stretching bands to higher energies; (ii) a variation in the absorbance ratio between asymmetric and symmetric stretching bands; and (iii) an overall reduction of the absorbances of the main PE bands.

A simple way of monitoring the melting process is to carefully analyze the vanishing of the doublets associated to the crystalline phase. On the other hand, if the physical mechanisms associated to other changes with temperature are known, it may be possible to extract valuable information about the PE dynamics under the influence of the presence of silica nanoparticles. As an example, different regions of the spectra have been considered (Fig. 5), showing the evolution of the absorbance with the temperature, band shifts and double peaks for the nanocomposite with a 3.3% by weight of silica nanoparticles. Similar results were obtained for the other samples. In order to monitor the changes in the crystallization process, the peaks at 719 cm⁻¹ and 1462 cm⁻¹ associated to the crystalline phases have been considered. A convenient way to analyze this effect is to study the ratio between the absorbance of the crystalline peak taken at its maximum and that of the closest minimum associated to the same mode in the amorphous phase. These ratios have been plotted in Fig. 6 for the different compositions studied.

Fig. 5 Evolution of the spectra with the temperature for the sample LDPE–3.3% SiO₂ 1h. Left: aliphatic stretching vibrations (ν_a, ν_s); center: bending mode of CH₂, δ(CH₂); right: rocking mode of the CH₂, γ_r(CH₂).

Fig. 6 Absorbance ratios of the bands corresponding to the rocking γ_r(CH₂) and bending δ(CH₂) modes of CH₂ as a function of temperature and nanosilica content. Left: R₇₂₉. Right, R₁₄₇₀.

As can be seen, both band ratios remain virtually constant when cooling from 140 °C to 120 °C as no crystalline phase is formed at all. However, at about 115 °C, the absorbance begins to increase indicating the formation of crystallites in which specific interactions are the responsible of the appearance of a new peak for the CH₂ rocking and bending modes. Beyond this point, the absorbance ratios increase constantly over the whole range of temperatures down to 40 °C. Two possible interpretations can be done here: either there is a continuous increase of the crystalline phase or there is a continuous increase of the density of the material due to cooling. Although both effects can contribute to the observed behavior, it seems reasonable to think that the increase in density be the most important contribution. In fact, the DSC experiments have shown that the offset of the exothermic peak due to crystallization appears at about 70 °C,¹³ when the crystallization has taken place. On the other hand, the silica nanoparticles do not seem to have any effect, either on the crystallization process or on the polymer dynamics.

When the integrated absorbance for the main IR bands is considered similar profiles are obtained. There is a continuous increase of this parameter as the temperature increases, with an important change of slope at 120 °C, which can be explained by the increase of density upon cooling. The most important change of slope is associated to the appearance of the crystalline phase from the amorphous phase, but little else can be said about the dynamics of the PE.

Finally, in order to study the global polymer dynamics of polyethylene, the absorbance ratio between the bands of the CH₂ stretching modes has been considered. The ratio, A₂₉₁₆/A₂₈₄₇, and its first derivative have been plotted in Fig. 7 as a function of temperature for all the different contents in SiO₂. It is observed how the ratio decreases when cooling down. Since the total absorbance increases with the temperature, the absorbance for the CH₂ asymmetric stretching mode has to diminish more slowly than that corresponding to the CH₂ symmetric stretching mode. A possible explanation is related to the different changes in the dipole moment with the volume.²² Asymmetric vibrations present a higher change in the dipole moment when the free volume increases with temperature. In other words, the continuous increase in the band ratio might be due to an increase in free volume that provides more space for segmental motions, allowing bigger changes in the dipole moment of the asymmetric vibrations and then a higher probability for the absorption to take place (higher absorbances). Therefore, when a certain polymer relaxation occurs, one would expect an enhancement of this effect or a change in the slope when plotting the absorbance ratio as a function of temperature. In fact, two important changes of slope are visualized in Fig. 7, which may be ascribed to thermal transitions of the PE.

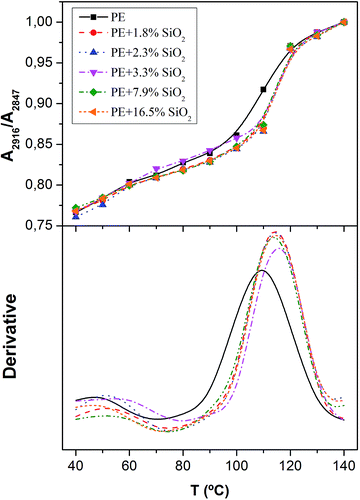Fig. 7 Absorbance ratio A₂₉₁₆/A₂₈₄₇ versus temperature (top) and its first derivative (bottom) for different contents in SiO₂ (dotted lines are the same as above).

To better identify the temperature at which those transitions occur faster, the first derivative of the absorbance ratio has been plotted in Fig. 7 (bottom). Regardless the nanosilica content, two maxima can be observed at about 55 °C and 120 °C, which nearly match the two thermal transitions obtained by DSC during heating and cooling scans.¹³ The relaxation occurring at 120° is entirely associated to the crystallization process,³⁷ while that centred at 60 °C can be attributed to a thermal relaxation, although its microscopic origin is still unclear. Up to present two are the possible explanations for that relaxation process. Some authors believe it comes from β-process, which is shifted to high temperatures because of the constraints imposed by the high entanglement density in the amorphous phase after crystallization, while others, assigned this relaxation to the α_I-process or an intralamellar slip process of mosaic blocks.³⁷

In terms of the effect of the presence of silica nanoparticles and by using this band ratio, it can be seen that the relaxation takes place at lower temperatures when there are no particles within the polymer. Besides, in the absence of silica the crystallization process seems to be more heterogeneous as it occurs along a wider interval of temperatures. This can be deduced from the first derivative of the absorbance ratio (Fig. 7 bottom) as a broader peak associated to the crystallization. Finally, at least from 1.8% to 16.5% wt of silica nanoparticles, the plots are coincident, which indicates that the PE dynamics is only slightly affected by the presence of a small amount of nanoparticles (lower than 1%), remaining then constant at higher loads of filler.

Conclusions

The use of FTIR-ATR spectroscopy to monitor IR spectra of the samples with temperature has allowed proposing an easy method to study thermal transitions as well as specific interactions at a molecular scale in a thermoplastic nanocomposite of LDPE and SiO₂. The analysis of the band absorption ratio of the aliphatic stretching vibrations (A₂₉₁₆/A₂₈₄₇) facilitated to obtain information of the overall polymer structure and dynamics. Thus, the relaxation phenomenon at about 55 °C in the nanocomposites filled with silica nanoparticles results to be slightly shifted to lower temperatures for LDPE without nanoparticles. Nanocomposites are usually claimed to produce extraordinary changes in the properties due to the high surface in contact with the matrix. In the case of LDPE–nanosilica, the degradation temperature of LDPE increases only when the amount of SiO₂ is relatively high, although its presence has not a noticeable catalytic or inhibiting effect on the decomposition of the polymer. The structural, morphological and thermal characterization of the nanocomposites did not reveal remarkable changes at low loads of filler either, indicating that in the case of LDPE–silica nanocomposites, where no strong interactions between the polymer and filler take place, the volume fraction of nanoparticles must be relatively high in order to produce noticeable changes in the bulk properties.

Acknowledgements

The authors acknowledge financial support from projects MAT2007-65752 and MAT2010-16815, and the assistance of S. Martínez with the TGA and FTIR-ATR experiments.

References

1. A. P. Kumar, D. Depan, N. S. Tomer and R. P. Singh, Prog. Polym. Sci., 2009, 34, 479.
2. R. Zhao, P. Torley and P. J. Halley, J. Mater. Sci., 2008, 43, 3058.
3. S. S. Ray and M. Okamoto, Prog. Polym. Sci., 2003, 28, 1539.
4. A. Yebra-Rodríguez, P. Alvarez-Lloret, C. Cardell and A. B. Rodríguez-Navarro, Appl. Clay Sci., 2009, 43, 91.
5. S. Molinaro, M. C. Romero, M. Boaro, A. Sensidoni, C. Lagazio, M. Morris and J. Kerry, J. Food Eng., 2013, 117, 113.
6. S. K. Sahoo, D. W. Kim, J. Kumar, A. Blumstein and A. L. Cholli, Macromolecules, 2003, 36, 2777.
7. H. Shinzawa, M. Nishida, T. Tanaka and W. Kanematsu, Vib. Spectrosc., 2012, 60, 50.
8. J. González-Benito and G. González-Gaitano, Macromolecules, 2008, 41, 4777.
9. J. Y. Nam, S. S. Ray and M. Okamoto, Macromolecules, 2003, 36, 7126.
10. F. Perrin-Sarazin, M. T. Ton-That, M. N. Bureau and J. Denault, Polymer, 2005, 46, 11624.
11. S. Zhao, L. S. Schadler, H. Hillborg and T. Auletta, Compos. Sci. Technol., 2008, 68, 2976.
12. J. González-Benito, J. Martínez-Tarifa, M. E. Sepúlveda-García, R. A. Portillo and G. González-Gaitano, Polym. Test., 2013, 32, 1342.
13. D. Olmos, E. Rodríguez-Gutiérrez and J. González-Benito, Polym. Compos., 2012, 33, 2009.
14. Y. Zhou, V. Rangari, H. Mahfuz, S. Jeelani and P. K. Mallick, Mater. Sci. Eng., A, 2005, 402, 109.
15. C. G. Martins, N. M. Larocca, D. R. Paul and L. A. Pessan, Polymer, 2009, 50, 1743.
16. J. González-Benito, J. Colloid Interface Sci., 2003, 267, 326.
17. P. Bartolomeo, J. F. Chailan and J. L. Vernet, Eur. Polym. J., 2001, 37, 659.
18. P. D. Castrillo, D. Olmos, J. M. Torkelson and J. González-Benito, Polym. Compos., 2010, 31, 781.
19. D. Olmos, A. Loayza and J. González-Benito, J. Appl. Polym. Sci., 2010, 117, 2695.
20. C. J. Ellison, K. E. Miller and J. M. Torkelson, Polymer, 2004, 45, 2623.
21. F. A. Sanchez, M. Redondo, D. Olmos, M. Kuzmanovic and J. González-Benito, Macromol. Symp., 2014, 339, 48.
22. D. Olmos, E. V. Martin and J. Gonzalez-Benito, Phys. Chem. Chem. Phys., 2014, 16, 24339.
23. P. D. Castrillo, D. Olmos, D. R. Amador and J. González-Benito, J. Colloid Interface Sci., 2007, 308, 318.
24. B. J. Ash, R. W. Siegel and L. S. Schadler, Macromolecules, 2004, 37, 1358.
25. D. Olmos, F. Martínez, G. González-Gaitano and J. González-Benito, Eur. Polym. J., 2011, 47, 1495.
26. D. Olmos, J. M. Martínez-Tarifa, G. González-Gaitano and J. González-Benito, Polym. Test., 2012, 31, 1121.
27. J. González-Benito, E. Castillo and J. F. Caldito, Eur. Polym. J., 2013, 49, 1747.
28. D. Olmos, A. García-López and J. González-Benito, Mater. Lett., 2013, 97, 8.
29. P. Paika and K. K. Kar, Mater. Chem. Phys., 2009, 113, 953.
30. H. E. Kissinger, Anal. Chem., 1957, 29, 1702.
31. A. Aboulkas, K. El Harfi and A. El Bouadili, Energy Convers. Manage., 2010, 51, 1363.
32. C. W. Bunn, Trans. Faraday Soc., 1939, 35, 482.
33. A. Charlesby, J. Polym. Sci., 1953, 10, 201.
34. S. Krimm, J. Chem. Phys., 1954, 22, 567.
35. J. J. Fox and A. E. Martin, Proc. R. Soc. London, Ser. A, 1940, 175, 208.
36. S. Krimm, C. Y. Liang and G. B. B. M. Sutherland, J. Chem. Phys., 1956, 25, 549.
37. Y. Men, J. Rieger, H. R. Endeler and D. Lilge, Macromolecules, 2003, 36, 4689.

---